【Vivado HLS学习之CORDIC算法的实现】

【Vivado HLS学习之CORDIC算法】

---

先抛出一个问题：在FPGA上怎么实现三角函数sin，cos的计算？
以sin为例，在计算机上实现sin函数可以用泰勒展开来近似。
$$sin(x)\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}+...$$

这种方式看似简单高效，但不便于FPGA上实现；
一个常见的方法是查表法：预先计算好各个相位对应的sin值，将这些数值保存在存储器中，计算时直接查表即可。这种方式的计算精度取决于数据表的长度，想要获得更高的精度，就需要占用更多的存储空间，是一种典型的“空间换时间”思路。

还有其他更合适FPAG的方法，比如CORDIC算法。

---

接下来介绍CORDIC算法。

CORDIC（Coordinate Rotation Digital Computer）算法即坐标旋转数字计算方法，是J.D.Volder1于1959年首次提出，主要用于三角函数、双曲线、指数、对数的计算。该算法通过基本的加和移位运算代替乘法运算，使得矢量的旋转和定向的计算不再需要三角函数、乘法、开方、反三角、指数等函数。

–摘自百度百科

单位圆上有A和B两点，夹角为θ。A点绕单位圆逆时针旋转θ角就能得到B点，假设A点坐标为(x1, y1)，B点坐标为(x2, y2)。坐标变换如下：
$$\{\begin{array}{cc}{x}_2=x_1\cos \theta -y_1\sin \theta & \\ y_2=x_1\sin \theta +y_1\cos \theta & \end{array}$$

将cosθ项提出，则得到
$$\{\begin{array}{cc}{x}_2=(x_1-y_1\tan \theta )\cos \theta & \\ y_2=(x_1\tan \theta +y_1)\cos \theta & \end{array}$$

(注意，如果A->B为顺时针旋转，则上述式中的加减号要互换)

CORDIC算法的思想就是，取一系列固定的角度θi，使得tanθi = 2^(-i)，这样一来tan乘积项就可以通过位移操作来实现；而这些固定的θi可以通过查表得到

θ(弧度)	tan(θ)
0.7853981633974483	1
0.4636476090008061	0.5
0.24497866312686414	0.25
0.12435499454676144	0.125
0.06241880999595735	0.0625
0.031239833430268277	0.03125
0.015623728620476831	0.015625
0.007812341060101111	0.0078125
0.0039062301319669718	0.00390625
0.0019531225164788188	0.001953125
0.0009765621895593195	0.0009765625
0.0004882812111948983	0.00048828125

至于cosθ，这一项在多次迭代后其累乘结果收敛于一定值K，用下面这一小段代码计算N次迭代后K的值，当N取12时
K = 0.607252959138945

# 计算N次迭代后, 余弦累乘项K
from math import cos, atan, prod
K = lambda N : prod([cos(atan(2**-i)) for i in range(N)])

print(K(12))

所以在迭代时，一开始就从点(K, 0)坐标旋转，按照上面正切表从上到下逐一旋转对应角度，注意旋转方向要向着靠近目标角度的方向。因为一开始就考虑到了K，所以最后迭代完成，旋转到一点的位置，其横坐标x就是cos值，纵坐标y就是sin值。

---

接下来考虑如何在FPGA上实现算法。使用Q4.12格式的定点数，也就是4位整数，12位小数。因为使用到了Vivado HLS工具，这里给出C语言实现的CORDIC算法，迭代12次，使用定点数运算。

cordic_cos_sin.c

#include 

#define PIPELINE 		12
#define FIXED_PI		((uint16)0x3243) // 3.14159*2^12


const int16 ROT_TABLE[]={				//旋转角对照表(弧度rad*2^12)
	0x0c90, 0x076b, 0x03eb, 0x01fd,
	0x00ff, 0x007f, 0x003f, 0x001f,
	0x000f, 0x0007, 0x0003, 0x0001
};


// 输入phase定点数 为 弧度*2^12
// 范围0~2pi*2^12
// 输出定点cos, sin
void cordic_cos_sin(
	uint16* phase,
	int16 * cos,
	int16 * sin
){
#pragma HLS INTERFACE port=return
    int16 x0= 0x09b7; 	// 0.60725*2^12 起点坐标
    int16 y0= 0; 		//
    int16 x1= 0; 		// 旋转到下一点的坐标
    int16 y1= 0; 		//
    int16 theta; 		// 起始角度
	uint2 quad; 		// 确定象限

#pragma HLS PIPELINE
	if (*phase < FIXED_PI/2){
		theta = *phase;
		quad = 0;
	}else if (*phase < FIXED_PI){
		theta = FIXED_PI - *phase;
		quad = 1;
	}else if (*phase < 3*FIXED_PI/2){
		theta = *phase - FIXED_PI;
		quad = 2;
	}else if (*phase < 2*FIXED_PI){
		theta = 2*FIXED_PI - *phase;
		quad = 3;
	}else{
		theta = 0;
		quad = 0;
	}

	// cordic迭代
	for (int i = 0; i < PIPELINE; i ++){
#pragma HLS UNROLL
		if (theta < 0){
			theta += ROT_TABLE[i];
            x1 = x0 + (y0 >> i); // x1 = x0 + y0 * tan(...)
            y1 = y0 - (x0 >> i); // y1 = y0 - x0 * tan(...)
		}else{
			theta -= ROT_TABLE[i];
            x1 = x0 - (y0 >> i); // x1 = x0 - y0 * tan(...)
            y1 = (x0 >> i) + y0; // y1 = x0 * tan(...) + y1
		}
		x0 = x1; // 更新
		y0 = y1;
	}

    switch (quad)
    {
        case 0:
			*cos = x1;
			*sin = y1;
            break;
        case 1:
			*cos = -x1;
			*sin = y1;
            break;
        case 2:
			*cos = -x1;
			*sin = -y1;
            break;
        case 3:
			*cos = x1;
			*sin = -y1;
            break;
        default:
            break;
    }
}

再写一个main.c作为testbench

main.c

#include 
#include 
#include 


#define TEST_LEN 100 // 测试100个数

// 待测函数
extern void cordic_cos_sin(
	uint16 *phase,
	int16 * cos,
	int16 * sin
);

int16 float2Q4_12(float f){
	return (int16) (f * pow(2, 12));
}

float Q4_12_2float(int16 i){
	return (float)( i / pow(2, 12));
}

int main(int argc, char const *argv[]){
	printf("********************* cordic test begin *********************\r\n");

	for (int16 i = 0; i < TEST_LEN; i++){
		float phase_f = 2 * i * M_PI / (float)TEST_LEN;
		uint16 phase_fixed = float2Q4_12(phase_f);

		float cos_real = cosf(phase_f);
		float sin_real = sinf(phase_f);
		int16 cos_cordic_fixed = 0;
		int16 sin_cordic_fixed = 0;
		cordic_cos_sin(&phase_fixed, &cos_cordic_fixed , &sin_cordic_fixed );
		float cos_cordic = Q4_12_2float(cos_cordic_fixed);
		float sin_cordic = Q4_12_2float(sin_cordic_fixed);

		printf("cos(%0.4f): %0.4f / %0.4f, err: %0.4f\t",\
				phase_f, cos_real, cos_cordic, cos_real - cos_cordic);
		printf("sin(%0.4f): %0.4f / %0.4f, err: %0.4f\r\n",\
				phase_f, sin_real, sin_cordic, sin_real - sin_cordic);
	}
	return 0;
}

下面是运行C仿真打印的结果

********************* cordic test begin *********************
cos(0.0000): 1.0000 / 1.0002, err: -0.0002	sin(0.0000): 0.0000 / 0.0000, err: 0.0000
cos(0.0628): 0.9980 / 0.9985, err: -0.0005	sin(0.0628): 0.0628 / 0.0632, err: -0.0004
cos(0.1257): 0.9921 / 0.9922, err: -0.0001	sin(0.1257): 0.1253 / 0.1257, err: -0.0004
cos(0.1885): 0.9823 / 0.9827, err: -0.0004	sin(0.1885): 0.1874 / 0.1877, err: -0.0004
cos(0.2513): 0.9686 / 0.9688, err: -0.0002	sin(0.2513): 0.2487 / 0.2488, err: -0.0001
cos(0.3142): 0.9511 / 0.9509, err: 0.0001	sin(0.3142): 0.3090 / 0.3098, err: -0.0008
cos(0.3770): 0.9298 / 0.9299, err: -0.0002	sin(0.3770): 0.3681 / 0.3684, err: -0.0003
cos(0.4398): 0.9048 / 0.9045, err: 0.0003	sin(0.43a98): 0.4258 / 0.4265, err: -0.0007
cos(0.5027): 0.8763 / 0.8760, err: 0.0003	sin(0.5027): 0.4818 / 0.4827, err: -0.0009
cos(0.5655): 0.8443 / 0.8442, err: 0.0001	sin(0.5655): 0.5358 / 0.5359, err: -0.0001
cos(0.6283): 0.8090 / 0.8091, err: -0.0001	sin(0.6283): 0.5878 / 0.5872, err: 0.0006
(省略)

可以看出误差还是比较小的，在10^-4数量级

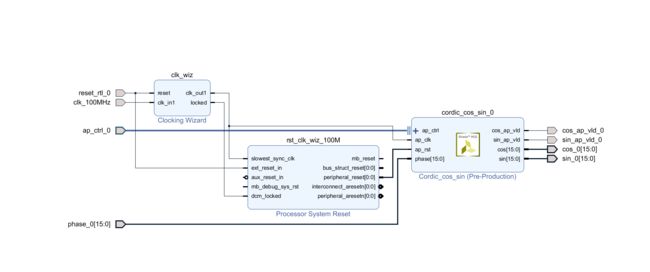
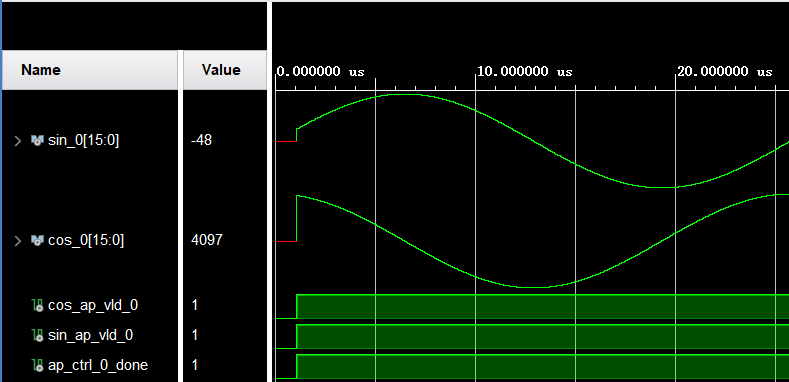
然后将模块打包成IP，导入Vivado测试：

block design

波形图

最后给出测试用的testbench.v

`timescale 1ns/100ps

module tb_cordic_sin_cos;
reg         clk;
reg         rst_n;
reg         input_en;
reg [15:0]  theta_rad_q4_12;

wire [15:0] cos_q4_12;
wire [15:0] sin_q4_12;
wire        output_en;

cordic_sin_cos u_0(
    .clk(clk),
    .rst_n(rst_n),
    .input_en(input_en),
    .theta_rad_q4_12(theta_rad_q4_12),
    .cos_q4_12(cos_q4_12),
    .sin_q4_12(sin_q4_12),
    .output_en(output_en)
);

localparam CLK_PERIOD = 10;
always #(CLK_PERIOD/2) clk=~clk;

initial begin
    $dumpfile("tb_cordic_sin_cos.vcd");
    $dumpvars(0, tb_cordic_sin_cos);
end

initial begin
    #1 rst_n<=1'bx;clk<=1'bx;
    theta_rad_q4_12 <= 0;
    input_en <= 0;
    #(CLK_PERIOD*3) rst_n<=1;
    #(CLK_PERIOD*3) rst_n<=0;clk<=0;
    repeat(5) @(posedge clk);
    rst_n<=1;
    input_en <= 1;
    
    for (integer i = 0; i < 25735; i = i + 10) begin
        @(negedge clk)
            theta_rad_q4_12 <= i;
    end
    $finish;
end

endmodule

---

感谢您的阅读，如有错误，欢迎指出