二叉树的基本内容（创建，遍历，节点个数，深度计算）

目录

写在前面的话

一，二叉树的遍历 

1.1三种遍历方式

1.2先序遍历（例子：LeetCode：144.二叉树的前序遍历）

题目分析

思路实现

二，二叉树的创建

2.1链表二叉树

2.2思路实现

2.3注意事项

2.4源码

三，二叉树的销毁

四，二叉树节点以及高度的计算

4.1二叉树节点个数

4.2二叉树叶子节点的个数

4.3二叉树第 k 层节点个数

4.4二叉树查找节点为 x 的节点

4.4求二叉树的深度

---

写在前面的话

小伙伴们大家好啊！今天小编为大家带来的是有关二叉树的内容，包括二叉树的创建，删除，遍历，以及求节点个数，判断二叉树是否是完全二叉树等内容，那么我们废话不多说，直接进入正题。

                                 

一，二叉树的遍历 

好的，那么我们知道，创建二叉树的时候，我们需要用到中序遍历去创建，所以我们先来了解一下有关遍历的内容。

1.1三种遍历方式

首先，我们对于二叉树三种遍历方式做一个简单的介绍：

先序遍历：先访问根节点，然后再访问左子树，最后再访问右子树。

中序遍历：先访问左子树，然后再访问根节点，最后再访问右子树。

后序遍历：先访问左子树，然后再访问右子树，最后再访问根节点。

因为道理都是相同的，只不过访问顺序不一样而已，所以这里我们以先序遍历为例来说明。

1.2先序遍历（例子：LeetCode：144.二叉树的前序遍历）

题目分析

题目中要求。我必须用动态内存开辟的空间将二叉树存储，并返回。 

思路实现

准备工作：

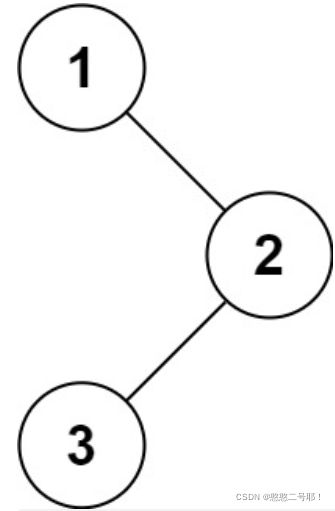
如下图所示，是一个二叉树，根据题目要求，我们需要通过动态内存开辟的空间去存储，所以首先我们需要知道二叉树节点个数，然后我们开辟完空间之后，才能进行存储。

 那么准备工作做完之后，我们进入真正的遍历。

遍历实现：

根据先序的特性，首先如果我们的头节点为空话，那么我们就可以直接返回空即可。

否则，首先我们需要建将该节点的值插入二叉树，然后在 计数器pi 自增之后，再去访问左子树，然后右子树，顺序一定是不能乱的。

源码实现：

int preorderSize(struct TreeNode* root)
{
    if(root==NULL)
      return 0;
    return preorderSize(root->left)+preorderSize(root->right)+1;
}

//但是函数实现 一般不需要返回值的时候，我们会将其设为 void
void _preorderTraversal(struct TreeNode* root,int *a,int *pi)
{
    if(root==NULL)
       return;
    a[(*pi)++]=root->val;
    
    _preorderTraversal(root->left,a,pi);
    _preorderTraversal(root->right,a,pi);

}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    //判断需要开辟多少空间
    int size = preorderSize(root);
    int * a = (int *)malloc(sizeof(int)*size); 
    //先序遍历
    int i=0;
    //该函数不需要返回值，因为节点数都放在了数组里面
    _preorderTraversal(root,a,&i);

    //返回值
    *returnSize=size;
    return a;
}

tips：对于上述这种 oj 题，输出型参数需要开辟空间，然后赋值返回的，各位小伙伴们在做题的时候，一定要记得哦！否则代码是通过不了的哦！  

二，二叉树的创建

那么首当其冲呢，需要先学会二叉树的创建，这里我们通过先序遍历的方式去建立一个二叉树，也就是说我们需要以二叉树先序遍历的规则去创建一个二叉树。那么为了方便我们查看最后创建的是否是正确的，我们可以通过任何一种二叉树的遍历去查看。

2.1链表二叉树

我们知道，二叉树不全是完全二叉树，所以如果用顺序表去实现所有的二叉树是存在一些问题的，比如下面这颗二叉树：

如果我们通过顺序表存储该二叉树，那么将有三个空间被浪费，如果二叉树很大的话，那么浪费可能更多，所以我们对于一般的二叉树的实现都是通过链表，这里就不会存在浪费空间的问题。

而对于完全二叉树而言，当然顺序表是更好地表示方式，因为顺序表有下标。 

2.2思路实现

如下图所示：首先，我们需要判断当前头节点是否为空，如果为空，在计数器 pi 的值加 1 之后，再将空返回；

反之，根据先序遍历的特性，首先将该节点插入，然后计数器自增 1 之后，再去创建该节点的左子树，然后当左子树为空返回之后，再去创建右子树。直到将 str 字符串表示的二叉树全部创建完成。

2.3注意事项

每次当节点不为空的时候，我们需要新增节点，然后再将其插入，所以每次在新增的时候，我们都需要在插入之前，用malloc函数去新增一个节点。

其次，因为 ++（自增） 的优先级高于 *（解引用），所以在计数器 pi 自增的时候，我么需要将其括起来，保证其先于解引用操作符使用。

2.4源码

对于源码这里做一些解释说明：

1.对于主函数而言，我们需要一个头节点来初始化二叉树，同时我们需要将一个字符串以及一个 计数器传递给创建函数。

2.这里我们将 # 作为空的替换，所以当节点的等于 # 的时候，就相当于节点为空。

3.遍历采用中序遍历（特性：访问次序：左根右），用其他两种方式也是可以的。

#include
#include
struct TreeNode
{
    struct TreeNode*left;
    struct TreeNode*right;
    char val;
};

struct TreeNode*creatTree(char *str,int* pi)
{
    if(str[*pi]=='#')
    {
        (*pi)++;
        return NULL;
    }
    struct TreeNode*root=(struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val=str[(*pi)++];
    root->left=creatTree(str,pi);
    root->right=creatTree(str,pi);
    return root;
}

void inOrder(struct TreeNode*root)
{
    if(root==NULL)
        return;
    inOrder(root->left);
    printf("%c ",root->val);
    inOrder(root->right);
}
int main()
{
    char str[100];
    int i=0;
    scanf("%s",str);
    struct TreeNode*root=creatTree(str,&i);
    inOrder(root);
   return 0;
}

三，二叉树的销毁

那么我们知道，如果你想销毁一颗链式二叉树，首先一定不能销毁的是根节点，否则后面的节点就没法访问了。所以这里我们采用二叉树后序遍历的思想去销毁。首先根节点的左子树和右子树，然后再销毁根节点。

四，二叉树节点以及高度的计算

好的，那么接下来我们对于二叉树的节点的以及高度的计算进行一个了解。

4.1二叉树节点个数

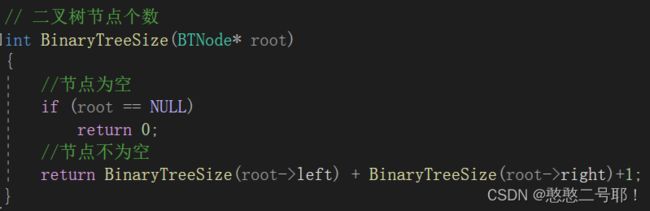
那么首先，我们需要知道对于二叉树而言，如果头节点为空，则表示没有一个节点，而当头节点不为空的时候，说明至少有一个节点。

然后同样的，将该二叉树的左子树作为头节点，再去计算当前二叉树的节点个数，然后再去计算右子树的节点个数，最后将其加起来，当然不能忘记的是，需要加上头节点的 1。

 如上代码所示，那么其实对于二叉树部分的结构，我们一般都会使用递归去实现，因为二叉树是一个相对而言比较对称的结构，所以当我们大事化小之后，思路会变得很简单。

4.2二叉树叶子节点的个数

上面我们对于二叉树的节点个数做了计算，那么其实对于叶子节点来说，稍微有点不同，但是思路都是相类似的。

如下代码所示：

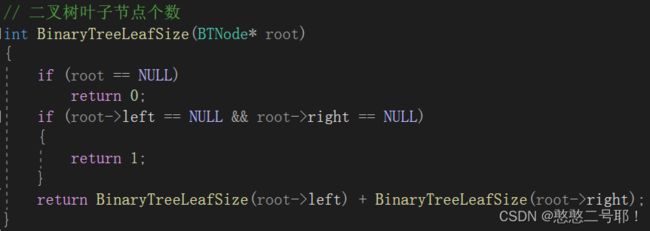
首先，依旧是如果根节点为空的时候，则直接返回空即可。

那么当头节点不为空的时候，就需要判断该头节点的左右子树是否为空，如果同时为空，则表示该节点为叶子节点，此时因为左右子树都为空，所以后面没有其他节点了，所以直接返回 1 即可。

最后如果第二步，头节点的左右子树不为空，说明当前根节点不是叶子节点，则需要再去将该二叉树的左子树和右子树分别作为根节点去判断。也就是重复上面的步骤。

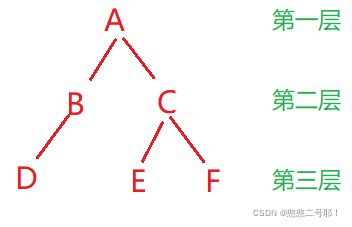
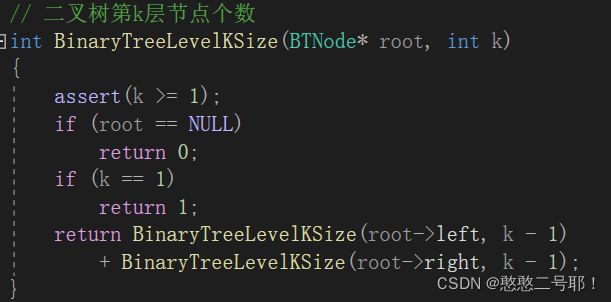
4.3二叉树第 k 层节点个数

那么对于第 k 层的节点，首先我们需要规定这样几个值，如下图所示：

如果当 k 为 0 时，也就是第 0 层时，这样是错误的（当然这里只是我们的规定，如果你想规定 A 节点为第 0 层也是可以实现的）。

那么对于具体实现来说，我们是这样的思路：依旧是递归。首先，我们认为求第 k 层节点个数，那么也就是求 k-1 层左右节点个数之和。

最主要的，除了递归之外，返回值类型是有两种的，第一种是当头节点为空的时候，直接返回空即可。第二种 是当 k 等于 1 的时候，也就是这一层就是需要求节点的那一层，如果当前节点存在，那么直接返回 1 ，同样的方式求出所有这一层的节点个数，并依次返回相加，最后得到的便是这一层的节点个数。

4.4二叉树查找节点为 x 的节点

那么对于查找来说，思路就比较简单了，首先如果当前节点为空的时候，说明找不到，直接返回空即可；其次，如果当前节点就是，直接返回该节点即可。

如果当前节点既不为空，同时不是查找的节点，此时就需要在该节点的左子树中和右子树中进行上面的查找。

这里先查左子树和先查右子树是没有区别的，如果查到了，那么直接返回即可。这里不能用与操作等，是因为没有必要，如果查找到了，直接一路返回到调用的函数，而不用再去访问右子树了。

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	//如果当前节点为查找的值，直接返回。
	if (root->data == x)
		return root;
	//如果当前root节点不是，则在该节点的左子树中找。
	BTNode* leftRet = BinaryTreeFind(root->left,x);
	//左子树两种情况，找到返回该节点，以及找不到返回NULL
	if (leftRet)
		return leftRet;
	//右子树一样的
	BTNode* rightRet = BinaryTreeFind(root->right,x);
	if (rightRet)
		return rightRet;
	//如果左右子树都返回空，说明找不到，则返回最后的空。
	return NULL;
}

4.4求二叉树的深度

二叉树的深度是所有子树中左子树或者右子树最多的那个路径的长度。

那么也即是说，当根节点为空的时候，表示当前深度为 0，不为空的时候，我们需要求出根节点左右子树的深度较大的那个加上根节点的长度 1；然后依次递归求出最深的那个长度。

//二叉树的深度
int BinaryTreeDepth(BTNode*root)
{
	if (root == NULL)
		return 0;
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

如上代码所示，我们先是求出了左右子树的深度值，然后再去比较。而不是将求值的过程也加入比较的环节。这样做的优势是：避免在比较出长度之后，在进行一次求值，也就是再进行一次刚才的递归操作，如果递归层次比较深的话，那么函数栈帧的开销是很大的，有可能导致栈溢出。

好的，那么本文到此就结束啦，如有问题，还请指正呀！