AtCoder Beginner Contest 232 题解（A-H）

A，B 略。

C 建出一张图的邻接矩阵然后用 next_permutation 枚举排列判断是否能建立映射即可。

D 简单网格 dp，注意边界条件。

ABC232E - Rook Path

$H\times W$ 的网格，你初始在 $(x_1,y_1)$，要求做 $K$ 次操作后位置变为 $(x_2,y_2)$。每次操作形如：

• 移动横坐标，从 $(x,y)$ 移动到 $(x^{\prime },y)$，其中 $1\le x^{\prime }\le H\wedge x^{\prime }\ne x$。
• 移动纵坐标，从 $(x,y)$ 移动到 $(x,y^{\prime })$，其中 $1\le y^{\prime }\le W\wedge y^{\prime }\ne y$。

（就是车的移动方式）问有多少种可能的操作方案，两种操作方案不同当且仅当中间某一步经过的点不同。答案对 $998244353$ 取模。

根据套路，这个东西的横向移动和纵向移动是可以分开来考虑的。即，我们可以考虑横向上走 $m$ 步的方案，再乘上纵向上走 $K-m$ 步的方案，再乘上组合系数 $\left(\genfrac{}{}{0ex}{}{K}{m}\right)$。考虑计算在一个方向上走 $m$ 步的方案数。

可以 DP，设 $f_{0/1,i}$ 表示横向移动（纵向的类似）回到出发点与否，走 $i$ 步的方案数，其中初始边界是 $f_{1,0}=1$，即走 $0$ 步，终点在原点的方案数为 $1$。转移如下：
$$\{\begin{array}{l}{f}_{1,i}=(H-1)f_{1,i-1}\\ f_{0,i}=f_{1,i-1}+(H-2)f_{0,i-1}\end{array}$$
转移的意义还是很显然的。于是我们 $O(n)$ 求出 dp 数组，这题就做完了，评测记录。

ABC232F - Simple Operations on Sequence

给定两个长度为 $N$（$2\le N\le 18$）：$A_i$ 和 $B_i$（$1\le A_i,B_i\le 10^8$）。可以进行如下两种操作，问最小的使得 $A$ 变成 $B$ 的操作代价：

• 对 $A_i$ 加一/减一，代价为 $X$（$1\le X\le 10^8$）
• 交换 $A$ 中的相邻元素，代价为 $Y$（$1\le Y\le 10^{16}$）

毫无疑问，两个操作是相互独立的，可以分开考虑。如果我们先交换，出一个 $P_1,P_2,\cdots ,P_N$ 的排列，然后再统计第一个的答案。令 $\mathrm{inv}(P)$ 为 $P$ 的逆序对数，则总代价为：
$$\sum _{i=1}^N|A_{P_i}-B_i|\cdot X+\mathrm{inv}(P)\cdot Y$$
把逆序对的这个关于 $i$ 的贡献拆开，则我们可以得到
$$\sum _{i=1}^N(|A_{P_i}-B_i|\cdot X+|\{p:p\in \{1,2,\cdots ,N\}\backslash \{P_1,\cdots ,P_{i-1}\},p<P_i\}|\cdot Y)$$
然后会发现一个很关键的地方：后面那个东西只和 $\{P_1,\cdots ,P_i\}$ 这个集合有关，而这个集合很小，所以不妨考虑将其状压起来，令 $f(x,S)$ 表示 $|p:p\in \{1,\cdots ,N\}\backslash S,p<x|$。然后式子改写为：
$$\sum _{i=1}^N(|A_{P_i}-B_i|\cdot X+f(P_i,\{P_1,\cdots ,P_{i-1}\})\cdot Y)$$
于是发现，这个东西可以状压 dp，具体地，设 $d{p}_S$ 表示排列的前 $|S|$ 项是 $S$ 内的元素，则转移应该是很好转移的。这题就做完了，评测记录。

ABC232G - Modulo Shortest Path

给定一张 $N$ 个点的有向完全图，其中，$i$ 到 $j$ 的有向边边权为 $(A_i+B_j)\mathrm{m}\mathrm{o}\mathrm{d}M$。问 $1$ 到 $N$ 的最短路。

$2\le N\le 2\times 10^5$，$2\le M\le 10^9$。

首先如果我们直接连边跑 Dij，那么必然会寄，边数是 $O(n^2)$ 级别的，要想办法少下来。

考虑一个技巧，建一张新图：

• 构建 $[0,M)$ 的虚点 $\overline{0},\overline{1},\cdots ,\overline{M-1}$。
• 然后 $\forall k\in [0,M-1)$，连边 $\overline{k}\to \overline{k+1}$，边权为 $1$。
• $\forall i\in [1,N]$，连边 $i\to \overline{-A_i\mathrm{m}\mathrm{o}\mathrm{d}M}$，边权为 $0$。
• $\forall i\in [1,N]$，连边 $\overline{B_i}$，边权为 $0$。

这样一来，从 $i$ 走到 $j$ 就相当于，从 $i$ 走到 $\overline{-A_i\mathrm{m}\mathrm{o}\mathrm{d}M}$，然后一步步走到 $\overline{B_j}$，再走到 $j$。发现中间的路程刚好就是 $(A_i+B_j)\mathrm{m}\mathrm{o}\mathrm{d}M$，于是问题就得到了转化，我们求新图上 $1$ 到 $N$ 的最短路即可。

可是，$O(n+m)$ 似乎也必死无疑。

然而我们可以发现，环上的很多点是没有用的，我们可以将其缩起来，会和原来的点连接的虚点只有 $2n$ 个，这样子点数和边数就都控制在了 $O(n)$ 级别，直接跑 Dij 便可通过，时间复杂度 $O(n\log n)$，评测记录。

ABC232H - King’s Tour

不知道组题人怎么想的。。。这个题居然放在 H。

给定 $H\times W$ 棋盘，一个国王初始在 $(1,1)$。国王每步可以走到与其八连通的格子，请构造一个方案使得国王不重复地走完了每个格子，且终点为 $(a,b)$。$2\le H,W\le 100$，$(a,b)\ne (1,1)$。

我们考虑减治构造。考虑如下几种情况：

$H=2$ 或 $W=2$

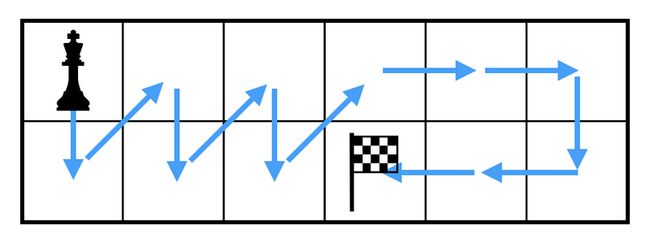
如果 $H=2$，那么就可以像下面这样构造方案（图源 AtCoder 官方题解）：

即，轨迹为：$(1,1)\to (2,1)\to \cdots \to (1,b)\to (1,b+1)\to \cdots \to (1,W)\to (2,W)\to \cdots \to (2,b)$。如果 $W=2$，那么将行列调换之后是一样的。

$H>2$ 且 $W>2$

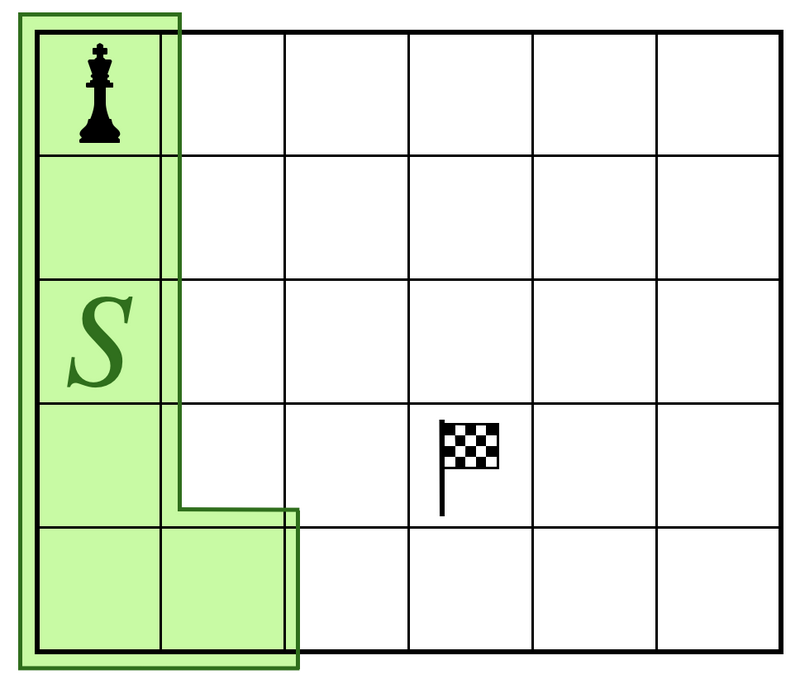
考虑下面这个方案：

绿色圈出来的点集为 $S$，分类讨论：

• $(a,b)\notin S$，则我们可以走完 $S$ 内的点，然后垂直翻转一下坐标系，就变成了一个一模一样的子问题，递归处理即可。
• $(a,b)\in S$，则我们交换行列之后，就变成了 $(a,b)\notin S$ 的情况。

然后就可以递归地去解决这道题了。这种代码写的很巧妙：

using pii = pair<int, int>;
 
vector<pii> solve(int h, int w, int a, int b) {
    vector<pii> ret;
    if (h == 2) {
        FOR(i, 1, b - 1) ret.push_back(pii(1, i)), ret.push_back(pii(2, i));
        ret.push_back(pii(3 - a, b));
        FOR(i, b + 1, w) ret.push_back(pii(1, i));
        DEC(i, w, b + 1) ret.push_back(pii(2, i));
        ret.push_back(pii(a, b));
    } else if ((h > 2 && w == 2) || b == 1 || (a == h && b == 2)) {
        ret = solve(w, h, b, a);
        for (auto &p : ret) myswap(p.first, p.second);
    } else {
        FOR(i, 1, h) ret.push_back(pii(i, 1));
        auto res = solve(h, w - 1, h + 1 - a, b - 1);
        for (auto &p : res) p.first = h + 1 - p.first, ++p.second;
        ret.insert(ret.end(), res.begin(), res.end());
    }
    return ret;
}
 
int main() {
    int h, w, a, b; read(h, w, a, b);
    auto ans = solve(h, w, a, b);
    for (auto p : ans) print(p.first, p.second);
    return output(), 0;
}