数据结构(排序)
文章目录
- 一、排序的概念
- 二、插入排序
-
- 1. 基本思想
- 2. 直接插入排序
- 3. 希尔排序(缩小增量排序)
- 三、选择排序
-
- 1. 基本思想
- 2. 直接选择排序
- 3. 堆排序
- 四、交换排序
-
- 1. 基本思想
- 2. 冒泡排序
- 3. 快速排序
- 五、归并排序
- 六、其他排序
-
- 6.1 计数排序
- 6.2 基数排序
- 6.3 桶排序
一、排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定。
稳定性的意义:
同样的任务先完成的是我们主观定义的第一,但是同样的任务完成了但是比前者慢,这是客观的第一。稳定性可以让本该是第一的就排在前面。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序(磁盘或文件的外层上排序)
常见的排序算法:
- 插入排序 选择排序 交换排序 归并排序
- 直接插入排序 选择排序 冒泡排序 归并排序
- 希尔排序 堆排序 快速排序
二、插入排序
1. 基本思想
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列,如我们玩扑克牌理牌的时候
2. 直接插入排序
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= 0; j--) {
//这里加一个等号 就不是一个稳定的排序了
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
//array[j+1] = tmp;
break;
}
}
array[j+1] = tmp;
}
}
- 时间复杂度
- 最好情况下:O(n) -> 数据有序的情况下 1 2 3 4 5
- 最坏情况下:O(n^2) -> 数据逆序的情况下 5 4 3 2 1
- 当数据越有序的时候 直接插入排序的效率越高
- 空间复杂度 O(1)
- 稳定性:稳定
- 一个本身就稳定的排序 可以实现为不稳定
- 但是一个本身就不稳定的排序 不可能实现为稳定的排序
3. 希尔排序(缩小增量排序)
基本思想
- 分组,缩小增量
- 组内进行插入排序(相当于进行预排序,使其趋向于有序)
private static void shell(int[] array,int gap) {
//不是把某一组去走完,而是交替地去排序
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0; j -= gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
//array[j+gap] = tmp;
break;
}
}
array[j+gap] = tmp;
}
}
public static void shellSort(int[] array) {
int gap = array.length;//7
while (gap > 1) {
gap /= 2;//1
shell(array,gap);
}
//shell(array,1);
}
- 时间复杂度
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定。这里暂时按照 n^1.3 去算
- 空间复杂度 O(1)
- 稳定性:不稳定
- 其他特性:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果(结合直接插入排序的时间复杂度去理解)
三、选择排序
1. 基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
2. 直接选择排序
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array,minIndex,i);
}
}
private static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void selectSort2(int[] array) {
int left = 0;
int right = array.length-1;
while (left < right) {
int minIndex = left;
int maxIndex = left;
for (int i = left+1; i <= right; i++) {
if(array[i] < array[minIndex]) {
minIndex = i;
}
if(array[i] > array[maxIndex]) {
maxIndex = i;
}
}
swap(array,minIndex,left);
if(maxIndex == left) {
maxIndex = minIndex;
}
swap(array,maxIndex,right);
left++;
right--;
}
}
private static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
- 时间复杂度
- O(n^2) 不管你本身的数据 是有序还是无序 都是这个复杂度
- 空间复杂度 O(1)
- 稳定性:不稳定
3. 堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆
public static void heapSort(int[] array) {
createBigHeap(array);
int end = array.length-1;
while (end > 0) {
swap(array,end,0);
siftDown(array,0,end);
end--;
}
}
private static void createBigHeap(int[] array) {
for (int i = (array.length-1-1) / 2; i >= 0 ; i--) {
siftDown(array,i,array.length);
}
}
private static void siftDown(int[] array,int parent,int len) {
int child = 2*parent+1;
while (child < len) {
if(child+1 < len && array[child] < array[child+1]) {
child++;
}
if(array[child] > array[parent]) {
swap(array,child,parent);
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}
- 时间复杂度
- O(n*logn) 对数据不敏感 不管有序无序都是这个表达式
- 空间复杂度 O(1)
- 稳定性:不稳定
四、交换排序
1. 基本思想
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动
2. 冒泡排序
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
boolean flg = false;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
swap(array,j,j+1);
flg = true;
}
}
//如果这次排序没有交换,说明已经是有序的了,可以直接退出
if(!flg) {
break;
}
}
}
- 时间复杂度
- O(N^2) 对数据不敏感 有序 无序都是这个复杂度!
- 加了优化之后,时间复杂度可能会变成O(n)
- 空间复杂度 O(1)
- 稳定性:稳定
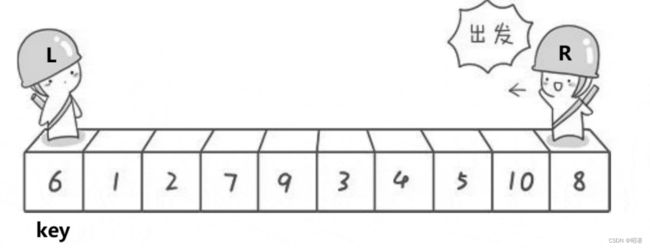
3. 快速排序
逆序很慢
优先使用挖坑法,然后是hoare,最后是前后指针法
1. 基础框架
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int[] array, int left, int right)
{
if(right - left <= 1)
return;
// 按照基准值对array数组的 [left, right)区间中的元素进行划分
int div = partion(array, left, right);
// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
// 递归排[left, div)
QuickSort(array, left, div);
// 递归排[div+1, right)
QuickSort(array, div+1, right);
}
- 时间复杂度
- O(n*logN)[最好情况,完全二叉树] O(N^2)[数据是有序的 或者是逆序的 ]
- 空间复杂度:O(logN)[好的情况] O(n) [不好的情况]
- 稳定性:不稳定排序
快速排序递归实现的主框架,与二叉树前序遍历规则非常像,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可,下面介绍几种将区间按照基准值划分为左右两半部分的方式
public static int parttion1(int[] array,int left,int right) {
int i = left;//记录这个位置
int tmp = array[left];
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
//todo: 先检查前面的会不会有问题
while (left < right && array[left] <= tmp) {
left++;
}
swap(array,left,right);
}
swap(array,left,i);
return left;
}
public static void quick(int[] array,int start,int end) {
if(start >= end) {
return;
}
int pivot = parttion(array,start,end);
quick(array,start,pivot-1);//左树
quick(array,pivot+1,end);//右树
}
3. 挖坑法
private static int parttion(int[] array,int left,int right) {
int tmp = array[left];
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
//todo: 先检查前面的会不会有问题
while (left < right && array[left] <= tmp) {
left++;
}
array[right] = array[left];
}
array[left] = tmp;
return left;
}
4. 前后指针法
//写法一
private static int partition(int[] array, int left, int right) {
int prev = left ;
int cur = left+1;
while (cur <= right) {
if(array[cur] < array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,left);
return prev;
}
//写法二
private static int partition(int[] array, int left, int right) {
int d = left + 1;
int pivot = array[left];
for (int i = left + 1; i <= right; i++) {
if (array[i] < pivot) {
swap(array, i, d);
d++;
}
}
swap(array, d - 1, left);
return d - 1;
}
5. 快速排序优化
(1)三数取中
让树两边都能被分配到内容,即比较最左边和最右边和中间的值,取中值放在最左边
private static int threeNum(int[] array,int left,int right) {
int mid = (left+right) / 2;
if(array[left] < array[right]) {
if(array[mid] < array[left]) {
return left;
}else if(array[mid] > array[right]) {
return right;
}else {
return mid;
}
}else {
if(array[mid] < array[right]) {
return right;
}else if(array[mid] > array[left]) {
return left;
}else {
return mid;
}
}
}
private static void quick(int[] array, int start, int end){
if (start >= end) {
return;
}
int mid = threeNum(array, start, end);
swap(array, mid, start);
int pivot = parttion(array, start, end);
quick(array, start, pivot - 1);
quick(array, pivot + 1, end);
}
(2)递归到小的子区间时,可以考虑使用插入排序
因为后面的元素个数过多
private static void insertSort2(int[] array,int left,int right) {
for (int i = left+1; i <= right; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= left; j--) {
//这里加一个等号 就不是一个稳定的排序了
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
//array[j+1] = tmp;
break;
}
}
array[j+1] = tmp;
}
}
public static int count = 0;
private static void quick(int[] array,int start,int end) {
if(start >= end) {
return;
}
count++;
if(end - start +1 <= 20) {
//直接插入排序
insertSort2(array,start,end);
return;
}
//三数取中
int mid = threeNum(array,start,end);
//交换
swap(array,mid,start);
int pivot = parttion(array,start,end);
quick(array,start,pivot-1);//左树
quick(array,pivot+1,end);//右树
}
(3)快速排序非递归
//无优化
void quickSortNonR(int[] a, int left, int right) {
Stack<Integer> st = new Stack<>();
st.push(left);
st.push(right);
while (!st.empty()) {
right = st.pop();
left = st.pop();
if(right - left <= 1){
continue;
}
int div = PartSort1(a, left, right);
// 以基准值为分割点,形成左右两部分:[left, div) 和 [div+1, right)
st.push(div+1);
st.push(right);
st.push(left);
st.push(div);
}
}
//加了优化
public static void quickSort(int[] array) {
Stack<Integer> stack = new Stack<>();
int start = 0;
int end = array.length-1;
if(end - start +1 <= 20) {
//直接插入排序
insertSort2(array,start,end);
return;
}
//三数取中
int mid = threeNum(array,start,end);
//交换
swap(array,mid,start);/**/
int pivot = parttion(array,start,end);
if(pivot > start+1) {
stack.push(start);
stack.push(pivot-1);
}
if(pivot < end-1) {
stack.push(pivot+1);
stack.push(end);
}
while (!stack.empty()) {
end = stack.pop();
start = stack.pop();
if(end - start +1 <= 20) {
//直接插入排序
insertSort2(array,start,end);
//return; 这个地方不能return
}else {
mid = threeNum(array,start,end);
//交换
swap(array,mid,start);/**/
pivot = parttion(array, start, end);
if (pivot > start + 1) {
stack.push(start);
stack.push(pivot - 1);
}
if (pivot < end - 1) {
stack.push(pivot + 1);
stack.push(end);
}
}
}
}
五、归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
(1)非递归写法
private static void merge(int[] array,int left,int mid,int right) {
int s1 = left;
int e1 = mid;
int s2 = mid+1;
int e2 = right;
int[] tmpArr = new int[right-left+1];
int k = 0;//tmpArr数组的下标
while (s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]){
tmpArr[k++] = array[s1++];
}else {
tmpArr[k++] = array[s2++];
//s2++;
//k++;
}
}
while (s1 <= e1) {
tmpArr[k++] = array[s1++];
}
while (s2 <= e2) {
tmpArr[k++] = array[s2++];
}
for (int i = 0; i < k; i++) {
array[i+left] = tmpArr[i];
}
}
private static void mergeSortFunc(int[] array,int left,int right) {
if(left >= right) {
return;
}
int mid = (left+right) / 2;
mergeSortFunc(array,left,mid);
mergeSortFunc(array,mid+1,right);
merge(array,left,mid,right);//合并
}
(2)递归式写法
public static void mergeSort(int[] array) {
int gap = 1;
while (gap < array.length) {
for (int i = 0; i < array.length; i = i + gap*2) {
int left = i;
int mid = left+gap-1;
int right = mid+gap;
//mid 和 right 有可能会越界
if(mid >= array.length) {
//纠正
mid = array.length-1;
}
if(right >= array.length) {
right = array.length-1;
}
merge(array,left,mid,right);
}
gap *= 2;
}
}
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定的排序
六、其他排序
6.1 计数排序
public static void countArray(int[] array) {
//1、找到数组当中的最大值和最小值 O(N)
int maxVal = array[0];
int minVal = array[0];
for (int i = 1; i < array.length; i++) {
if(array[i] < minVal) {
minVal = array[i];
}
if(array[i] > maxVal) {
maxVal = array[i];
}
}
//2、可以确定计数数组的大小 O(N)
int range = maxVal - minVal + 1;
int[] count = new int[range];
//3、再次遍历原来的数组 把原来的数据 和 计数数组的下标进行对应,来计数
for (int i = 0; i < array.length; i++) {
int val = array[i];
count[val-minVal]++;//这里开始计数 假设val是92 minVal = 91
}
//4、上述循环走完 计数数组已经存好了对应关系 ,遍历计数数组 O(范围+n)
int index = 0;//记录重新写会array数组的下标
for (int i = 0; i < count.length; i++) {
int val = count[i];
while (val != 0) {
array[index] = i + minVal;
val--;
index++;
}
}
}
- 时间复杂度:O(范围+n) 范围越小复杂度越快
- 空间复杂度:O(范围)
- 稳定性:稳定的排序
- 计数排序适合于 给定范围且范围不大。浪费空间来换取时间
6.2 基数排序
原理:将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数
public class RadixSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int maxDigit = getMaxDigit(arr);
return radixSort(arr, maxDigit);
}
/**
* 获取最高位数
*/
private int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLenght(maxValue);
}
private int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
protected int getNumLenght(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
private int[] radixSort(int[] arr, int maxDigit) {
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
return arr;
}
/**
* 自动扩容,并保存数据
*
* @param arr
* @param value
*/
private int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}