在 Python 中构建卷积神经网络； 从 0 到 9 的手绘数字的灰度图像预测数字

一、说明

        为了预测从0到9的数字，我选择了一个基于著名的Kaggle的MNIST数据集的数据集。数据集包含从 <0> 到 <9> 的手绘图数字的灰度图像。在本文中，我将根据像素数据（即数值数据）和卷积神经网络预测数字。

二、 卷积神经网络

        卷积神经网络，也称为 CNN 或 ConvNet，是一种人工神经网络，迄今为止最常用于分析计算机视觉任务的图像。

        尽管图像分析是CNNS最广泛的用途，但它们也可用于其他数据分析或分类。让我们开始吧！

        一般来说，我们可以将CNN视为一种人工神经网络，它具有某种类型的专业化，能够挑选或检测模式。这种模式检测使CNN在图像分析中如此有用。

        但是，如果CNN只是一个人工神经网络，那么它与标准的多层感知器或MLP有什么区别呢？

        CNN有称为卷积层的隐藏层，这些层是构成CNN的，嗯......一个美国有线电视新闻网！

CNN具有称为卷积层的层。

CNN可以，而且通常也有其他非卷积层，但CNN的基础是卷积层。

好的，那么这些卷积层是做什么的呢？

就像任何其他层一样，卷积层接收输入，以某种方式转换输入，然后将转换后的输入输出到下一层。卷积层的输入称为输入通道，输出称为输出通道。

对于卷积层，发生的转换称为卷积操作。无论如何，这是深度学习社区使用的术语。在数学上，卷积层执行的卷积运算实际上称为互相关。

如前所述，卷积神经网络能够检测图像中的模式。

让我们扩展一下我们的意思 当我们说过滤器能够检测模式时。想想任何单个图像中可能发生了什么。多个边缘、形状、纹理、对象等。这就是我们所说的模式。

• 边缘
• 形状
• 纹理
• 曲线
• 对象
• 颜色

滤波器可以在图像中检测到的一种图案是边缘，因此该滤波器称为边缘检测器。

除了边缘之外，某些过滤器可能会检测到角落。有些人可能会检测到圆圈。其他，正方形。现在这些简单的几何滤波器 就是我们在卷积神经网络开始时看到的。

网络越深入，过滤器就越复杂。在后面的图层中，我们的过滤器可能能够检测特定的物体，而不是边缘和简单的形状，如眼睛、耳朵、头发或毛皮、羽毛、鳞片和喙。

在更深的层中，过滤器能够检测到更复杂的物体，如完整的狗、猫、蜥蜴和鸟类。

三、 数据理解

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import random
import itertools
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, Dropout, Flatten, MaxPooling2D
import osdf = pd.read_csv("MNIST_ROI.csv")

3.1 探索性分析

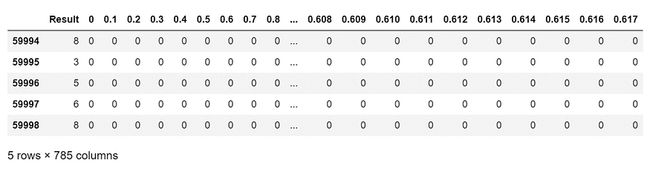
df.shape

(59999, 785)

数据集包括 59，999 条记录和 785 个字段。每条记录代表手绘图数字的灰度图像，介于 0 到 9 之间。

第一列称为“结果”，是用户绘制的数字。

其余列包含关联图像的像素值。每个灰度图像的高度为 28 像素，宽度为 28 像素，总共 784 像素。

df.head()

每个像素都有一个与之关联的像素值，指示该像素的明暗度，数字越大意味着越亮。此像素值是介于 0（黑色）和 255（白色）之间的整数（包括 <>（黑色）和 <>（白色）。

df.tail()

df.info()

df.describe()

3.2 数据分析

让我们检查数据集中每个数字有多少张图像

dig = [0,1,2,3,4,5,6,7,8,9]
num = []
for i in range(0,10):
    num.append(len(df[df['Result']==i]))
    
d = {'Digit': dig, 'Count': num}
df1 = pd.DataFrame(data=d)
df1

import matplotlib.pyplot as plt
import seaborn as sns
sns.barplot(x = “Count”, y = “Digit”, data = df2, orient=’h’)
plt.show()

让我们看看数据集中的哪些行中有数字“3”的图像

df[df[‘Result’]==3].head()

让我们打印第 6 行的图像

pic = df[6:7].values.reshape(785)[1:].reshape(28,28)
plt.imshow(pic,cmap='gray')

让我们看看数据集中的哪些行中有数字“5”的图像

df[df[‘Result’]==5].head()

让我们打印第 10 行的图像

pic = df[10:11].values.reshape(785)[1:].reshape(28,28)
plt.imshow(pic,cmap=’gray’)

四、数据准备

 X = df.drop(['Result'],axis=1)X.head() 

 y = df.Resulty.head() 

import sklearn.model_selection as skmodelX_train, X_test, y_train, y_test = skmodel.train_test_split(X, y, test_size=0.33, random_state=42)print("length of all data is ","{:,}".format(len(X)))
print("length of training set is","{:,}".format(len(X_train)))
print("length of test set is","{:,}".format(len(X_test))) 

X_train.head()

y_train.head()

让我们将训练集和测试集从 pandas.core.frame.DataFrame 转换为 numpy.ndarray

x_train = np.array(X_train)
y_train = np.array(y_train)
x_test = np.array(X_test)
y_test = np.array(y_test)len(X_train)

40199

让我们画一个介于 0 到 40199 之间的数字

i = random.randint(0,(len(X_train)))
i

34944

现在，让我们打印训练集中第 34944 行的图像结果

print(y_train[i])

3

让我们打印训练集中第 34944 行的图像

pic = X_train.iloc[i].values.reshape(28,28)plt.imshow(pic, cmap=’Greys’)

x_train.shape

(40199, 784)

让我们将数组重塑为 4 个 dimnsions，以便它可以与 Keras API 一起使用

x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
input_shape = (28, 28, 1)

让我们确保值是浮点数的，以便我们可以在除法后获得小数点

x_train = x_train.astype('float32')
x_test = x_test.astype('float32') 

现在，让我们通过将 RGB 代码除以最大 RGB 值来规范化 RGB 代码

x_train /= 255
x_test /= 255print('x_train shape:', x_train.shape)
print('Number of images in x_train', x_train.shape[0])
print('Number of images in x_test', x_test.shape[0])

五、建模

让我们使用顺序模型构建一个 CNN 并添加层：

model = Sequential()
model.add(Conv2D(28, kernel_size=(3,3), input_shape=input_shape))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten()) # Flattening the 2D arrays for fully connected layers
model.add(Dense(128, activation=tf.nn.relu))
model.add(Dropout(0.2))
model.add(Dense(10,activation=tf.nn.softmax))

让我们编译我们的CNN

model.compile(optimizer=’adam’, loss=’sparse_categorical_crossentropy’,  metrics=[‘accuracy’])

现在，让我们训练我们的CNN

model.fit(x=x_train,y=y_train, epochs=10)

训练集准确率：99.37%

model.evaluate(x_test, y_test)

测试装置准确率：98.22%

训练集的准确率为 99.37%，而测试集的准确率为 98.22%。这表明卷积神经网络（CNN）很好地推广到新数据，而不是过度拟合。

六、评估

len(X_test)

19800

让我们画一个介于 0 到 19800 之间的数字

j = random.randint(0,(len(X_test)))
j

11092

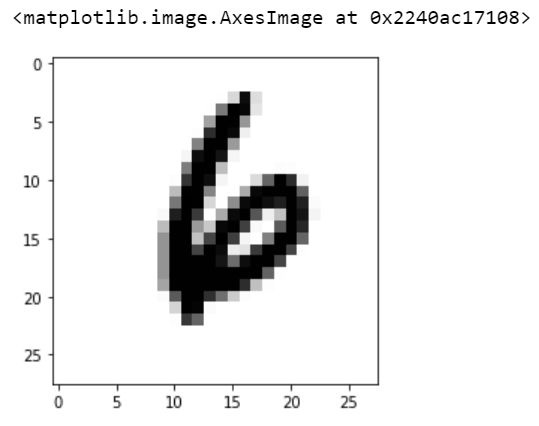
现在，让我们对测试集中第 11092 行的图像结果进行预测

pred = model.predict(x_test[j].reshape(1, 28, 28, 1))print(pred.argmax())

6

让我们打印测试集中第 11092 行的图像

pic1 = X_test.iloc[j].values.reshape(28,28)
plt.imshow(pic1, cmap='Greys')

y_pred = model.predict(x_test)
y_pred = np.argmax(y_pred,axis=1)
y_pred.shape

(19800, )

6.1 混淆矩阵

import sklearn.metrics as skmetcm = skmet.confusion_matrix(y_true=y_test, y_pred=y_pred)def plot_confusion_matrix(cm, classes,
 normalize=False,
 title=’Confusion matrix’,
 cmap=plt.cm.Blues):
 “””
 This function prints and plots the confusion matrix.
 Normalization can be applied by setting `normalize=True`.
 “””
 plt.imshow(cm, interpolation=’nearest’, cmap=cmap)
 plt.title(title)
 plt.colorbar()
 tick_marks = np.arange(len(classes))
 plt.xticks(tick_marks, classes, rotation=45)
 plt.yticks(tick_marks, classes)print(‘Confusion matrix, without normalization’)
print(cm)
thresh = cm.max() / 2.for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
 plt.text(j, i, cm[i, j],
 horizontalalignment=”center”,
 color=”white” if cm[i, j] > thresh else “black”)
plt.tight_layout()
plt.ylabel(‘True label’)
plt.xlabel(‘Predicted label’)cm_plot_labels = [‘0’,’1',’2',’3',’4',’5',’6',’7',’8',’9']plot_confusion_matrix(cm=cm, classes=cm_plot_labels, title=’Confusion Matrix’)

print(“\033[1m The result is telling us that we have: “,(cm[0,0]+cm[1,1]+cm[2,2]+cm[3,3]+cm[4,4]+cm[5,5]+cm[6,6]+cm[7,7]+cm[8,8]+cm[9,9]),”correct predictions.”)
print(“\033[1m The result is telling us that we have: “,(cm.sum()-(cm[0,0]+cm[1,1]+cm[2,2]+cm[3,3]+cm[4,4]+cm[5,5]+cm[6,6]+cm[7,7]+cm[8,8]+cm[9,9])),”incorrect predictions.”)
print(“\033[1m We have total predictions of: “,(cm.sum()))

6.2 计算精度、召回率、f 分数和支持

        引用Scikit Learn的话：

        精度是比率 tp / （tp + fp），其中 tp 是真阳性数，fp 是误报数。精度直观地是分类器在样本为阴性时不将其标记为阳性的能力。

        召回率是比率 tp / （tp + fn），其中 tp 是真阳性的数量，fn 是假阴性的数量。召回率直观地是分类器找到所有阳性样本的能力。

        f1 分数可以解释为精度和召回率的加权调和平均值，其中 f1 分数在 1 达到其最佳值，在 0 时达到最差分数。

        f1 分数将召回率的权重比精度高 1.0 倍，这意味着召回率和精度同样重要。

        支持是每个类在y_test中的出现次数。

print(skmet.classification_report(y_test, y_pred))

七、部署

        因此，我们的卷积神经网络（CNN）模型是一个很好的模型，可以从0到9的手绘数字的灰度图像中预测数字。现在，我们如何从新的灰度图像中预测数字？

len(X_test)

19800

        让我们画一个介于 0 到 19800 之间的数字

k = random.randint(0,(len(X_test)))
k

766

        让我们使用我们的模型预测来自 pred1 的数字

pred1 = model.predict(x_train[k].reshape(1, 28, 28, 1))
print(pred1.argmax())

7

        我们的模型说我们画了一个数字“7”的图像。因此，让我们打印此图像以查看我们的模型是否正确

pic2 = X_train.iloc[k].values.reshape(28,28)
plt.imshow(pic2, cmap='Greys')

是的！我们的模型是正确的。

八、总结

        卷积神经网络（ConvNet/CNN）是一种深度学习算法，可以接收输入图像，为图像中的各个方面/对象分配重要性（可学习的权重和偏差），并能够区分彼此。

        卷积神经网络的架构类似于人脑中神经元的连接模式，并受到视觉皮层组织的启发。

        单个神经元仅在称为感受野的视野的受限区域中对刺激做出反应。

        此类字段的集合重叠以覆盖整个视觉区域。