理智点

cs231n assignment1 q4

文章目录

嫌啰嗦直接看源码
Q4: two_layer_net
- affine_forward
- - 题面
  - 解析
  - 代码
  - 输出
- affine_backward
- - 推导
  - 题面
  - 解析
  - 代码
  - 输出
- relu_forward
- - 题面
  - 解析
  - 代码
  - 输出
- relu_backward
- - 题面
  - 解析
  - 代码
  - 输出
- svm_loss
- - 题面
  - 解析
  - 代码
  - 输出
- softmax_loss
- - 题面
  - 解析
  - 代码
  - 输出
- fc_net
- - \_\_init_\_
  - - 题面
    - 解析
    - 代码
  - loss
  - - 题面
    - 解析
    - 代码
- Solver
- - 题面
  - 解析
  - 代码
  - 输出
- Tune your hyperparameters
- - 题面
  - 代码
  - 结果
- 最后的输出

嫌啰嗦直接看源码

往期作业
cs231n作业 assignment 1 q1 q2 q3

Q4: two_layer_net

就是让我们训练一个神经网络，跟着教程一步一步走就好了

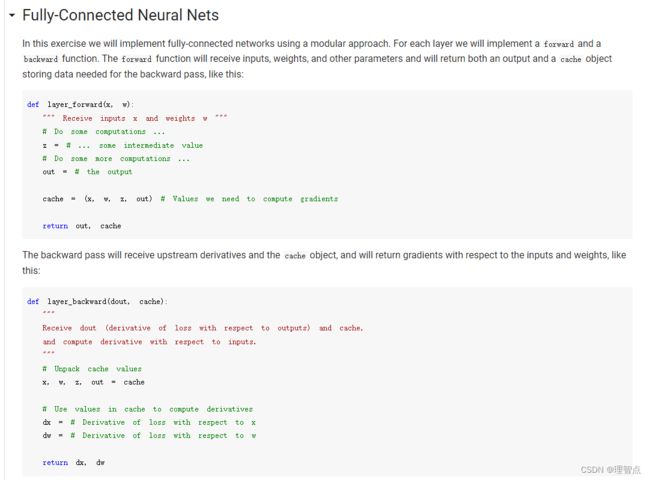
affine_forward

题面

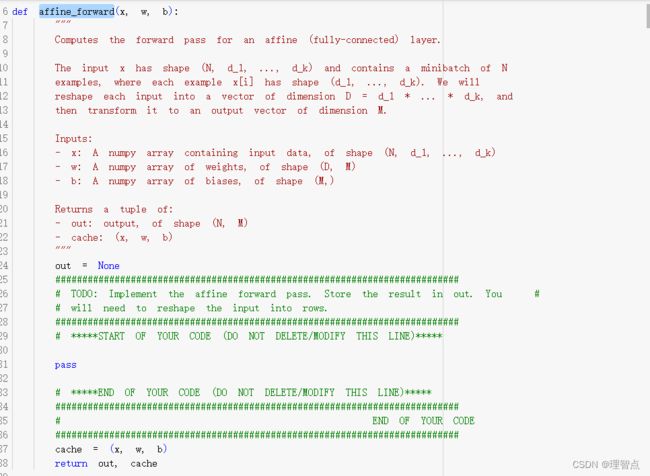
让我们实现一下前向传播的代码，同时让我们对输入的X进行维度转换，就像之前的q1 q2 q3 中教程帮我们做的一样

解析

我觉得没啥好说的，如果说X的维度转换不会的话，可以翻看前面的ipynb，里面又怎么转换的方法，或者直接看我的代码

代码

def affine_forward(x, w, b):
    """
    Computes the forward pass for an affine (fully-connected) layer.

    The input x has shape (N, d_1, ..., d_k) and contains a minibatch of N
    examples, where each example x[i] has shape (d_1, ..., d_k). We will
    reshape each input into a vector of dimension D = d_1 * ... * d_k, and
    then transform it to an output vector of dimension M.

    Inputs:
    - x: A numpy array containing input data, of shape (N, d_1, ..., d_k)
    - w: A numpy array of weights, of shape (D, M)
    - b: A numpy array of biases, of shape (M,)

    Returns a tuple of:
    - out: output, of shape (N, M)
    - cache: (x, w, b)
    """
    out = None
    ###########################################################################
    # TODO: Implement the affine forward pass. Store the result in out. You   #
    # will need to reshape the input into rows.                               #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    out = x.reshape((x.shape[0],-1)) @ w + b

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, w, b)
    return out, cache

输出

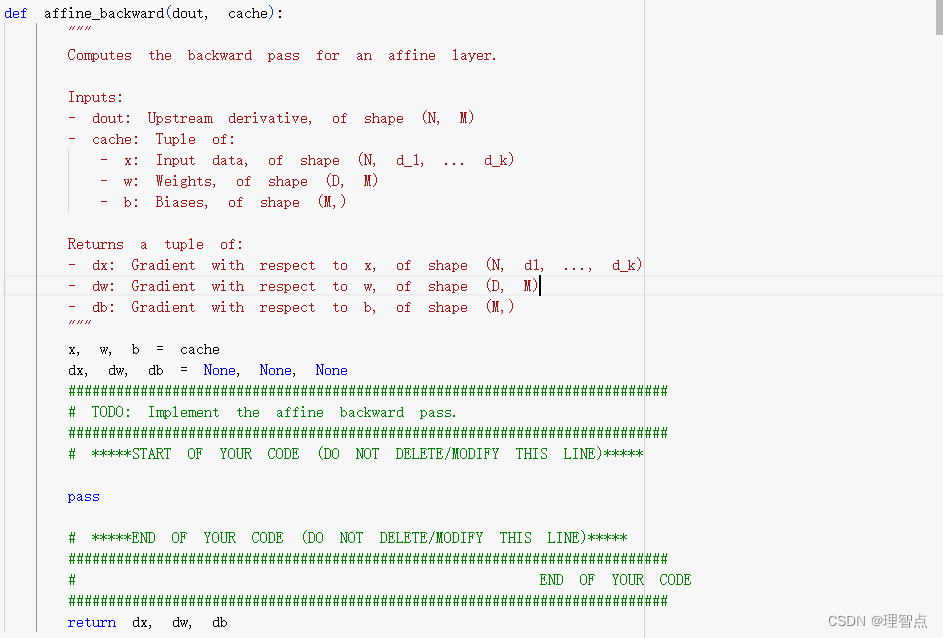
affine_backward

推导

题面

就是让我们求dx,dw,db，注意题目需要的shape

解析

看推导就行了，推导看懂了就不需要解析了

代码

def affine_backward(dout, cache):
    """
    Computes the backward pass for an affine layer.

    Inputs:
    - dout: Upstream derivative, of shape (N, M)
    - cache: Tuple of:
      - x: Input data, of shape (N, d_1, ... d_k)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)

    Returns a tuple of:
    - dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
    - dw: Gradient with respect to w, of shape (D, M)
    - db: Gradient with respect to b, of shape (M,)
    """
    x, w, b = cache
    dx, dw, db = None, None, None
    ###########################################################################
    # TODO: Implement the affine backward pass.                               #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    dx = (dout @ w.T).reshape(x.shape)
    dw = x.reshape((x.shape[0],-1)).T @ dout
    db = np.sum(dout,axis = 0)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dw, db

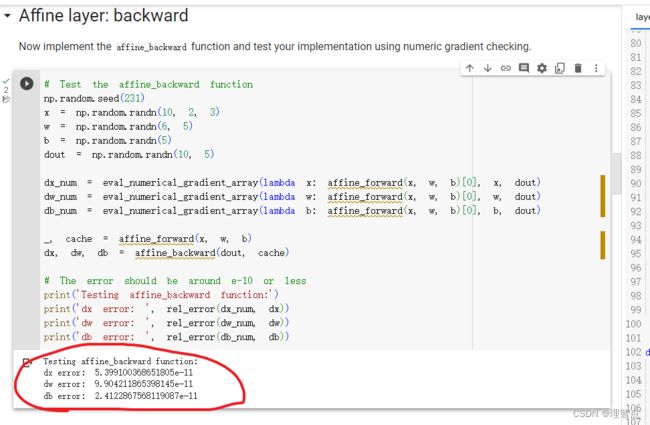
输出

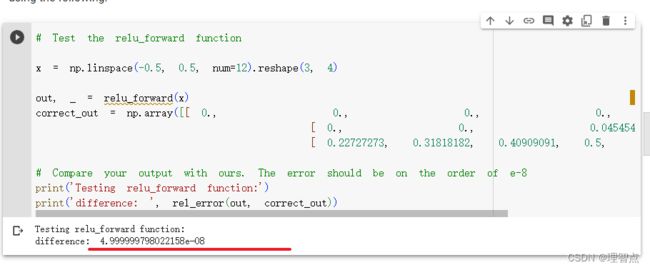
relu_forward

 ReLU的公式是：f(x) = max(0,x)

题面

解析

这个太蠢了，就是如果x的元素小于0就赋值为零就好了，用np.maximum就完事了

代码

def relu_forward(x):
    """
    Computes the forward pass for a layer of rectified linear units (ReLUs).

    Input:
    - x: Inputs, of any shape

    Returns a tuple of:
    - out: Output, of the same shape as x
    - cache: x
    """
    out = None
    ###########################################################################
    # TODO: Implement the ReLU forward pass.                                  #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    out = np.maximum(0,x)

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = x
    return out, cache

输出

relu_backward

题面

解析

因为relu(x) = max(0,x)
所以如果x < 0,那么该点的梯度为0，因此只需要将dout中对应 x < 0 的位置的元素变成0就行，其他位置不动

代码

def relu_backward(dout, cache):
    """
    Computes the backward pass for a layer of rectified linear units (ReLUs).

    Input:
    - dout: Upstream derivatives, of any shape
    - cache: Input x, of same shape as dout

    Returns:
    - dx: Gradient with respect to x
    """
    dx, x = None, cache
    ###########################################################################
    # TODO: Implement the ReLU backward pass.                                 #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    dx = np.multiply(dout, (x > 0)) 

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx

输出

svm_loss

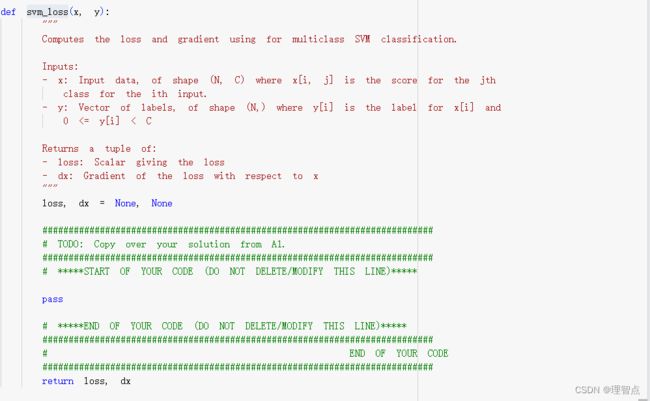
题面

解析

就是跟之前一样的计算svm的loss和梯度，不知道怎么做的话可以看我往期的文章
但是又跟之前的不一样，之前的梯度计算是需要求到仿射层的就是相当于要求到(dL) / (dW)的
但是这里不一样，这个我们只需要求到(dL) / (dy),就是只需要求softmax_loss的梯度，不需要在细致的求到每个w的梯度了（而且想让我们求，我们也没有足够的条件求）

代码

def svm_loss(x, y):
    """
    Computes the loss and gradient using for multiclass SVM classification.

    Inputs:
    - x: Input data, of shape (N, C) where x[i, j] is the score for the jth
      class for the ith input.
    - y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
      0 <= y[i] < C

    Returns a tuple of:
    - loss: Scalar giving the loss
    - dx: Gradient of the loss with respect to x
    """
    loss, dx = 0, 0

    ###########################################################################
    # TODO: Copy over your solution from A1.
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    # 样本数量
    num_train = x.shape[0]

    # 获取正确分类的分数
    scores_correct = x[range(num_train),y].reshape((x.shape[0],1))
    margins = np.maximum(0,x - scores_correct + 1)
    # 将正确分类的分数置为0
    margins[range(num_train),y] = 0
    loss += np.sum(margins)
    # 正则项
    loss /= num_train

    # 计算梯度
    margins[margins > 0] = 1
    row_sum = np.sum(margins,axis = 1)
    margins[range(num_train),y] = -row_sum
    dx = margins
    dx /= num_train
    

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return loss, dx

输出

放到和softmax_loss的一起了，因为是一起输出的结果

softmax_loss

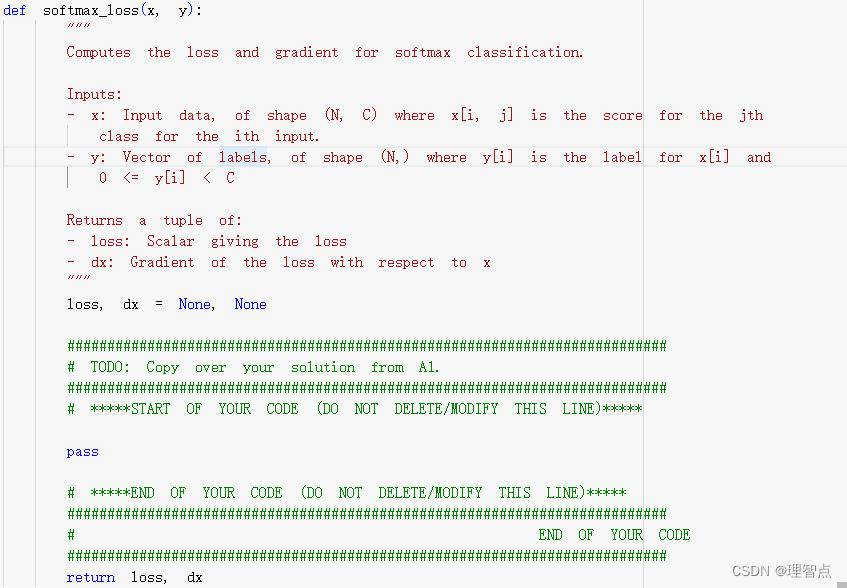
题面

意思同上，就是计算softmax的loss和梯度

解析

同上，不会的话看往期的文章，不过注意这次我加了个数值稳定函数，无伤大雅的，不用也行

代码

def softmax_loss(x, y):
    """
    Computes the loss and gradient for softmax classification.

    Inputs:
    - x: Input data, of shape (N, C) where x[i, j] is the score for the jth
      class for the ith input.
    - y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
      0 <= y[i] < C

    Returns a tuple of:
    - loss: Scalar giving the loss
    - dx: Gradient of the loss with respect to x
    """
    loss, dx = 0, 0

    ###########################################################################
    # TODO: Copy over your solution from A1.
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    # 训练数据的数量
    num_train = x.shape[0]

    # 先取e的幂函数
    scores = np.exp(x- x.max(axis=1, keepdims=True))
    # 上面有种增加数值稳定的函数，防止指数函数太大爆炸影响真正的效果
    # scores = np.exp(x- x.max(axis=1, keepdims=True)) 其中的-x.max（axis=1,keepdims=True）就是增加数值稳定的
    # 当然对于本题的数据，我们直接用np.exp(x)也可以的 ^_^
    # 计算所有的概率
    p = scores / np.sum(scores,axis = 1,keepdims = True)
    # 计算loss函数
    loss += np.sum(-np.log(p[range(num_train),y]))

    # 计算梯度 根据公式可以知道只要给正确分类的P - 1就可以得到dW
    p[range(num_train),y] -= 1
    dx += p


    # 计算正则项
    loss /= num_train
    dx /= num_train



    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return loss, dx

输出

看上面的条件，基本都符合了

fc_net

这个让我们实现一个两层的神经网络，一层是Relu，一层是softmax

网络的结构
affine - relu - affine - softmax.

init

题面

按照题目的自已就是让我们自己初始化一下训练用到的参数，其中w是符合高斯分布的随机数，b全是0

解析

np.random.normal()来生成w

np.zeros()来生成b

代码

    def __init__(
        self,
        input_dim=3 * 32 * 32,
        hidden_dim=100,
        num_classes=10,
        weight_scale=1e-3,
        reg=0.0,
    ):
        """
        Initialize a new network.

        Inputs:
        - input_dim: An integer giving the size of the input
        - hidden_dim: An integer giving the size of the hidden layer
        - num_classes: An integer giving the number of classes to classify
        - weight_scale: Scalar giving the standard deviation for random
          initialization of the weights.
        - reg: Scalar giving L2 regularization strength.
        """
        self.params = {}
        self.reg = reg

        ############################################################################
        # TODO: Initialize the weights and biases of the two-layer net. Weights    #
        # should be initialized from a Gaussian centered at 0.0 with               #
        # standard deviation equal to weight_scale, and biases should be           #
        # initialized to zero. All weights and biases should be stored in the      #
        # dictionary self.params, with first layer weights                         #
        # and biases using the keys 'W1' and 'b1' and second layer                 #
        # weights and biases using the keys 'W2' and 'b2'.                         #
        ############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        self.params.W1 = np.random.normal(loc=0.0,scale=weight_scale,size=(input_dim,hidden_dim))
        self.params.W2 = np.random.normal(loc=0.0,scale=weight_scale,size=(hidden_dim,num_classes))
        self.params.b1 = np.zeros((hidden_dim,))
        self.params.b2 = np.zeros((num_classes,))


        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

loss

题面

解析

一步一步来，主要是别忘了几个正则项，经过这样子网络的结构，对于我们调用的时候其实已经代码书写难度已经大大降低了，稍加思考对应元素的位置就好了

代码

def loss(self, X, y=None):
        """
        Compute loss and gradient for a minibatch of data.

        Inputs:
        - X: Array of input data of shape (N, d_1, ..., d_k)
        - y: Array of labels, of shape (N,). y[i] gives the label for X[i].

        Returns:
        If y is None, then run a test-time forward pass of the model and return:
        - scores: Array of shape (N, C) giving classification scores, where
          scores[i, c] is the classification score for X[i] and class c.

        If y is not None, then run a training-time forward and backward pass and
        return a tuple of:
        - loss: Scalar value giving the loss
        - grads: Dictionary with the same keys as self.params, mapping parameter
          names to gradients of the loss with respect to those parameters.
        """
        scores = None
        ############################################################################
        # TODO: Implement the forward pass for the two-layer net, computing the    #
        # class scores for X and storing them in the scores variable.              #
        ############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        W1 = self.params['W1']
        W2 = self.params['W2']
        b1 = self.params['b1']
        b2 = self.params['b2']


        affine_1_out,affine_1_cache = affine_forward(X,W1,b1)
        relu_out,relu_cache = relu_forward(affine_1_out)
        affine_2_out,affine_2_cache = affine_forward(relu_out,W2,b2)
        # 这里不走softmax层了，因为softmax层是计算loss值了，而这里我们只需要scores
        scores = affine_2_out


        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        # If y is None then we are in test mode so just return scores
        if y is None:
            return scores

        loss, grads = 0, {}
        ############################################################################
        # TODO: Implement the backward pass for the two-layer net. Store the loss  #
        # in the loss variable and gradients in the grads dictionary. Compute data #
        # loss using softmax, and make sure that grads[k] holds the gradients for  #
        # self.params[k]. Don't forget to add L2 regularization!                   #
        #                                                                          #
        # NOTE: To ensure that your implementation matches ours and you pass the   #
        # automated tests, make sure that your L2 regularization includes a factor #
        # of 0.5 to simplify the expression for the gradient.                      #
        ############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        # 用softmax计算loss和grad
        loss,d_affine_2_out = softmax_loss(affine_2_out,y)
        # loss 只需要算到这里，接下来加上正则项
        loss += 0.5 * self.reg * (np.sum(W1 * W1) + np.sum(W2 * W2)
)
        # 接下来算梯度
        d_relu_out,dW_2,dB_2 = affine_backward(d_affine_2_out,affine_2_cache)
        d_affine_1_out = relu_backward(d_relu_out,relu_cache)
        dX,dW_1,dB_1 = affine_backward(d_affine_1_out,affine_1_cache)

        dW_1 += self.reg * W1
        dW_2 += self.reg * W2

        # 保存梯度
        grads['W1'] = dW_1
        grads['W2'] = dW_2
        grads['b1'] = dB_1
        grads['b2'] = dB_2



        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        return loss, grads

Solver

题面

解析

就是让我们去阅读solver的代码，去熟悉我们自己写的几个api,然后构造一下我们solver就好了，代码很简单的，主要是阅读solver代码的过程

代码

input_size = 32 * 32 * 3
hidden_size = 50
num_classes = 10
model = TwoLayerNet(input_size, hidden_size, num_classes)
solver = None

##############################################################################
# TODO: Use a Solver instance to train a TwoLayerNet that achieves about 36% #
# accuracy on the validation set.                                            #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

solver = Solver(model, data, optim_config={'learning_rate': 1e-3})
solver.train()

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
#                             END OF YOUR CODE                               #
##############################################################################

输出

(Iteration 1 / 4900) loss: 2.301084
(Epoch 0 / 10) train acc: 0.109000; val_acc: 0.109000
(Iteration 11 / 4900) loss: 2.273729
(Iteration 21 / 4900) loss: 2.174355
(Iteration 31 / 4900) loss: 2.033214
(Iteration 41 / 4900) loss: 2.018372
(Iteration 51 / 4900) loss: 1.936294
(Iteration 61 / 4900) loss: 1.909365
(Iteration 71 / 4900) loss: 1.968080
(Iteration 81 / 4900) loss: 1.831189
(Iteration 91 / 4900) loss: 1.836682
(Iteration 101 / 4900) loss: 1.874288
(Iteration 111 / 4900) loss: 1.796551
(Iteration 121 / 4900) loss: 1.829135
(Iteration 131 / 4900) loss: 1.863156
(Iteration 141 / 4900) loss: 1.785416
(Iteration 151 / 4900) loss: 1.670677
(Iteration 161 / 4900) loss: 1.825214
(Iteration 171 / 4900) loss: 1.946122
(Iteration 181 / 4900) loss: 1.712422
(Iteration 191 / 4900) loss: 1.833139
(Iteration 201 / 4900) loss: 1.712148
(Iteration 211 / 4900) loss: 1.616144
(Iteration 221 / 4900) loss: 1.635851
(Iteration 231 / 4900) loss: 1.634573
(Iteration 241 / 4900) loss: 1.634086
(Iteration 251 / 4900) loss: 1.648923
(Iteration 261 / 4900) loss: 1.691381
(Iteration 271 / 4900) loss: 1.762122
(Iteration 281 / 4900) loss: 1.731388
(Iteration 291 / 4900) loss: 1.819805
(Iteration 301 / 4900) loss: 1.566611
(Iteration 311 / 4900) loss: 1.678215
(Iteration 321 / 4900) loss: 1.564199
(Iteration 331 / 4900) loss: 1.635177
(Iteration 341 / 4900) loss: 1.490303
(Iteration 351 / 4900) loss: 1.560792
(Iteration 361 / 4900) loss: 1.797754
(Iteration 371 / 4900) loss: 1.654941
(Iteration 381 / 4900) loss: 1.551228
(Iteration 391 / 4900) loss: 1.588600
(Iteration 401 / 4900) loss: 1.571287
(Iteration 411 / 4900) loss: 1.727028
(Iteration 421 / 4900) loss: 1.677506
(Iteration 431 / 4900) loss: 1.611189
(Iteration 441 / 4900) loss: 1.680913
(Iteration 451 / 4900) loss: 1.654809
(Iteration 461 / 4900) loss: 1.640508
(Iteration 471 / 4900) loss: 1.575345
(Iteration 481 / 4900) loss: 1.617710
(Epoch 1 / 10) train acc: 0.458000; val_acc: 0.450000
(Iteration 491 / 4900) loss: 1.651279
(Iteration 501 / 4900) loss: 1.684094
(Iteration 511 / 4900) loss: 1.578795
(Iteration 521 / 4900) loss: 1.562049
(Iteration 531 / 4900) loss: 1.603936
(Iteration 541 / 4900) loss: 1.539127
(Iteration 551 / 4900) loss: 1.543073
(Iteration 561 / 4900) loss: 1.499725
(Iteration 571 / 4900) loss: 1.567476
(Iteration 581 / 4900) loss: 1.897302
(Iteration 591 / 4900) loss: 1.573814
(Iteration 601 / 4900) loss: 1.404451
(Iteration 611 / 4900) loss: 1.618614
(Iteration 621 / 4900) loss: 1.680000
(Iteration 631 / 4900) loss: 1.670598
(Iteration 641 / 4900) loss: 1.589472
(Iteration 651 / 4900) loss: 1.600195
(Iteration 661 / 4900) loss: 1.352244
(Iteration 671 / 4900) loss: 1.578689
(Iteration 681 / 4900) loss: 1.650075
(Iteration 691 / 4900) loss: 1.465578
(Iteration 701 / 4900) loss: 1.483167
(Iteration 711 / 4900) loss: 1.427129
(Iteration 721 / 4900) loss: 1.784575
(Iteration 731 / 4900) loss: 1.415954
(Iteration 741 / 4900) loss: 1.511715
(Iteration 751 / 4900) loss: 1.487680
(Iteration 761 / 4900) loss: 1.373061
(Iteration 771 / 4900) loss: 1.665580
(Iteration 781 / 4900) loss: 1.430671
(Iteration 791 / 4900) loss: 1.326836
(Iteration 801 / 4900) loss: 1.426356
(Iteration 811 / 4900) loss: 1.498721
(Iteration 821 / 4900) loss: 1.377391
(Iteration 831 / 4900) loss: 1.374316
(Iteration 841 / 4900) loss: 1.507345
(Iteration 851 / 4900) loss: 1.662028
(Iteration 861 / 4900) loss: 1.468440
(Iteration 871 / 4900) loss: 1.569410
(Iteration 881 / 4900) loss: 1.388390
(Iteration 891 / 4900) loss: 1.467064
(Iteration 901 / 4900) loss: 1.505520
(Iteration 911 / 4900) loss: 1.779084
(Iteration 921 / 4900) loss: 1.490847
(Iteration 931 / 4900) loss: 1.429472
(Iteration 941 / 4900) loss: 1.598223
(Iteration 951 / 4900) loss: 1.690766
(Iteration 961 / 4900) loss: 1.494032
(Iteration 971 / 4900) loss: 1.522085
(Epoch 2 / 10) train acc: 0.483000; val_acc: 0.455000
(Iteration 981 / 4900) loss: 1.520685
(Iteration 991 / 4900) loss: 1.328689
(Iteration 1001 / 4900) loss: 1.394128
(Iteration 1011 / 4900) loss: 1.456969
(Iteration 1021 / 4900) loss: 1.621858
(Iteration 1031 / 4900) loss: 1.477229
(Iteration 1041 / 4900) loss: 1.462630
(Iteration 1051 / 4900) loss: 1.524669
(Iteration 1061 / 4900) loss: 1.515345
(Iteration 1071 / 4900) loss: 1.477645
(Iteration 1081 / 4900) loss: 1.470350
(Iteration 1091 / 4900) loss: 1.513094
(Iteration 1101 / 4900) loss: 1.544782
(Iteration 1111 / 4900) loss: 1.477012
(Iteration 1121 / 4900) loss: 1.364902
(Iteration 1131 / 4900) loss: 1.604127
(Iteration 1141 / 4900) loss: 1.536314
(Iteration 1151 / 4900) loss: 1.586519
(Iteration 1161 / 4900) loss: 1.463541
(Iteration 1171 / 4900) loss: 1.243605
(Iteration 1181 / 4900) loss: 1.481631
(Iteration 1191 / 4900) loss: 1.532539
(Iteration 1201 / 4900) loss: 1.249551
(Iteration 1211 / 4900) loss: 1.506066
(Iteration 1221 / 4900) loss: 1.427642
(Iteration 1231 / 4900) loss: 1.376686
(Iteration 1241 / 4900) loss: 1.566314
(Iteration 1251 / 4900) loss: 1.432466
(Iteration 1261 / 4900) loss: 1.567310
(Iteration 1271 / 4900) loss: 1.560503
(Iteration 1281 / 4900) loss: 1.595545
(Iteration 1291 / 4900) loss: 1.567085
(Iteration 1301 / 4900) loss: 1.454316
(Iteration 1311 / 4900) loss: 1.490910
(Iteration 1321 / 4900) loss: 1.592518
(Iteration 1331 / 4900) loss: 1.541783
(Iteration 1341 / 4900) loss: 1.374896
(Iteration 1351 / 4900) loss: 1.625951
(Iteration 1361 / 4900) loss: 1.471044
(Iteration 1371 / 4900) loss: 1.350735
(Iteration 1381 / 4900) loss: 1.609883
(Iteration 1391 / 4900) loss: 1.534862
(Iteration 1401 / 4900) loss: 1.452917
(Iteration 1411 / 4900) loss: 1.436169
(Iteration 1421 / 4900) loss: 1.405132
(Iteration 1431 / 4900) loss: 1.457032
(Iteration 1441 / 4900) loss: 1.494302
(Iteration 1451 / 4900) loss: 1.441696
(Iteration 1461 / 4900) loss: 1.606940
(Epoch 3 / 10) train acc: 0.483000; val_acc: 0.474000
(Iteration 1471 / 4900) loss: 1.399039
(Iteration 1481 / 4900) loss: 1.381901
(Iteration 1491 / 4900) loss: 1.395354
(Iteration 1501 / 4900) loss: 1.417236
(Iteration 1511 / 4900) loss: 1.484106
(Iteration 1521 / 4900) loss: 1.682362
(Iteration 1531 / 4900) loss: 1.469124
(Iteration 1541 / 4900) loss: 1.509884
(Iteration 1551 / 4900) loss: 1.484987
(Iteration 1561 / 4900) loss: 1.306599
(Iteration 1571 / 4900) loss: 1.355572
(Iteration 1581 / 4900) loss: 1.503104
(Iteration 1591 / 4900) loss: 1.492781
(Iteration 1601 / 4900) loss: 1.413251
(Iteration 1611 / 4900) loss: 1.560257
(Iteration 1621 / 4900) loss: 1.291057
(Iteration 1631 / 4900) loss: 1.286758
(Iteration 1641 / 4900) loss: 1.514361
(Iteration 1651 / 4900) loss: 1.518735
(Iteration 1661 / 4900) loss: 1.370597
(Iteration 1671 / 4900) loss: 1.469074
(Iteration 1681 / 4900) loss: 1.464342
(Iteration 1691 / 4900) loss: 1.384501
(Iteration 1701 / 4900) loss: 1.423517
(Iteration 1711 / 4900) loss: 1.417733
(Iteration 1721 / 4900) loss: 1.446887
(Iteration 1731 / 4900) loss: 1.320535
(Iteration 1741 / 4900) loss: 1.491887
(Iteration 1751 / 4900) loss: 1.498635
(Iteration 1761 / 4900) loss: 1.489212
(Iteration 1771 / 4900) loss: 1.542994
(Iteration 1781 / 4900) loss: 1.514106
(Iteration 1791 / 4900) loss: 1.304327
(Iteration 1801 / 4900) loss: 1.222466
(Iteration 1811 / 4900) loss: 1.378112
(Iteration 1821 / 4900) loss: 1.393398
(Iteration 1831 / 4900) loss: 1.345431
(Iteration 1841 / 4900) loss: 1.474607
(Iteration 1851 / 4900) loss: 1.278975
(Iteration 1861 / 4900) loss: 1.423413
(Iteration 1871 / 4900) loss: 1.470634
(Iteration 1881 / 4900) loss: 1.523484
(Iteration 1891 / 4900) loss: 1.494911
(Iteration 1901 / 4900) loss: 1.549876
(Iteration 1911 / 4900) loss: 1.506629
(Iteration 1921 / 4900) loss: 1.377911
(Iteration 1931 / 4900) loss: 1.431192
(Iteration 1941 / 4900) loss: 1.377486
(Iteration 1951 / 4900) loss: 1.415583
(Epoch 4 / 10) train acc: 0.506000; val_acc: 0.476000
(Iteration 1961 / 4900) loss: 1.618262
(Iteration 1971 / 4900) loss: 1.492193
(Iteration 1981 / 4900) loss: 1.454406
(Iteration 1991 / 4900) loss: 1.359818
(Iteration 2001 / 4900) loss: 1.285706
(Iteration 2011 / 4900) loss: 1.371012
(Iteration 2021 / 4900) loss: 1.359123
(Iteration 2031 / 4900) loss: 1.498010
(Iteration 2041 / 4900) loss: 1.354732
(Iteration 2051 / 4900) loss: 1.438783
(Iteration 2061 / 4900) loss: 1.480778
(Iteration 2071 / 4900) loss: 1.537145
(Iteration 2081 / 4900) loss: 1.188694
(Iteration 2091 / 4900) loss: 1.282485
(Iteration 2101 / 4900) loss: 1.342001
(Iteration 2111 / 4900) loss: 1.548787
(Iteration 2121 / 4900) loss: 1.572799
(Iteration 2131 / 4900) loss: 1.343591
(Iteration 2141 / 4900) loss: 1.586770
(Iteration 2151 / 4900) loss: 1.293524
(Iteration 2161 / 4900) loss: 1.547009
(Iteration 2171 / 4900) loss: 1.408669
(Iteration 2181 / 4900) loss: 1.455682
(Iteration 2191 / 4900) loss: 1.168711
(Iteration 2201 / 4900) loss: 1.277475
(Iteration 2211 / 4900) loss: 1.269945
(Iteration 2221 / 4900) loss: 1.315483
(Iteration 2231 / 4900) loss: 1.362125
(Iteration 2241 / 4900) loss: 1.415312
(Iteration 2251 / 4900) loss: 1.362131
(Iteration 2261 / 4900) loss: 1.511428
(Iteration 2271 / 4900) loss: 1.207401
(Iteration 2281 / 4900) loss: 1.415940
(Iteration 2291 / 4900) loss: 1.425663
(Iteration 2301 / 4900) loss: 1.295703
(Iteration 2311 / 4900) loss: 1.254505
(Iteration 2321 / 4900) loss: 1.497928
(Iteration 2331 / 4900) loss: 1.251498
(Iteration 2341 / 4900) loss: 1.382769
(Iteration 2351 / 4900) loss: 1.288472
(Iteration 2361 / 4900) loss: 1.458135
(Iteration 2371 / 4900) loss: 1.313538
(Iteration 2381 / 4900) loss: 1.387674
(Iteration 2391 / 4900) loss: 1.306602
(Iteration 2401 / 4900) loss: 1.450026
(Iteration 2411 / 4900) loss: 1.420869
(Iteration 2421 / 4900) loss: 1.248337
(Iteration 2431 / 4900) loss: 1.327928
(Iteration 2441 / 4900) loss: 1.505570
(Epoch 5 / 10) train acc: 0.493000; val_acc: 0.458000
(Iteration 2451 / 4900) loss: 1.339375
(Iteration 2461 / 4900) loss: 1.391034
(Iteration 2471 / 4900) loss: 1.574944
(Iteration 2481 / 4900) loss: 1.508791
(Iteration 2491 / 4900) loss: 1.304072
(Iteration 2501 / 4900) loss: 1.440362
(Iteration 2511 / 4900) loss: 1.305748
(Iteration 2521 / 4900) loss: 1.488807
(Iteration 2531 / 4900) loss: 1.615756
(Iteration 2541 / 4900) loss: 1.405928
(Iteration 2551 / 4900) loss: 1.246385
(Iteration 2561 / 4900) loss: 1.315364
(Iteration 2571 / 4900) loss: 1.421446
(Iteration 2581 / 4900) loss: 1.497967
(Iteration 2591 / 4900) loss: 1.331557
(Iteration 2601 / 4900) loss: 1.453666
(Iteration 2611 / 4900) loss: 1.285519
(Iteration 2621 / 4900) loss: 1.425636
(Iteration 2631 / 4900) loss: 1.314801
(Iteration 2641 / 4900) loss: 1.298306
(Iteration 2651 / 4900) loss: 1.461723
(Iteration 2661 / 4900) loss: 1.523801
(Iteration 2671 / 4900) loss: 1.415812
(Iteration 2681 / 4900) loss: 1.318759
(Iteration 2691 / 4900) loss: 1.469690
(Iteration 2701 / 4900) loss: 1.262966
(Iteration 2711 / 4900) loss: 1.489861
(Iteration 2721 / 4900) loss: 1.228969
(Iteration 2731 / 4900) loss: 1.468175
(Iteration 2741 / 4900) loss: 1.349398
(Iteration 2751 / 4900) loss: 1.271159
(Iteration 2761 / 4900) loss: 1.391232
(Iteration 2771 / 4900) loss: 1.357391
(Iteration 2781 / 4900) loss: 1.417309
(Iteration 2791 / 4900) loss: 1.522723
(Iteration 2801 / 4900) loss: 1.526235
(Iteration 2811 / 4900) loss: 1.331352
(Iteration 2821 / 4900) loss: 1.329435
(Iteration 2831 / 4900) loss: 1.088911
(Iteration 2841 / 4900) loss: 1.695192
(Iteration 2851 / 4900) loss: 1.439629
(Iteration 2861 / 4900) loss: 1.304997
(Iteration 2871 / 4900) loss: 1.327335
(Iteration 2881 / 4900) loss: 1.360054
(Iteration 2891 / 4900) loss: 1.608956
(Iteration 2901 / 4900) loss: 1.301895
(Iteration 2911 / 4900) loss: 1.286987
(Iteration 2921 / 4900) loss: 1.465441
(Iteration 2931 / 4900) loss: 1.436922
(Epoch 6 / 10) train acc: 0.494000; val_acc: 0.441000
(Iteration 2941 / 4900) loss: 1.214374
(Iteration 2951 / 4900) loss: 1.442676
(Iteration 2961 / 4900) loss: 1.182191
(Iteration 2971 / 4900) loss: 1.540090
(Iteration 2981 / 4900) loss: 1.329494
(Iteration 2991 / 4900) loss: 1.255908
(Iteration 3001 / 4900) loss: 1.693805
(Iteration 3011 / 4900) loss: 1.482947
(Iteration 3021 / 4900) loss: 1.518969
(Iteration 3031 / 4900) loss: 1.261443
(Iteration 3041 / 4900) loss: 1.125180
(Iteration 3051 / 4900) loss: 1.384420
(Iteration 3061 / 4900) loss: 1.449550
(Iteration 3071 / 4900) loss: 1.422641
(Iteration 3081 / 4900) loss: 1.317469
(Iteration 3091 / 4900) loss: 1.427890
(Iteration 3101 / 4900) loss: 1.226803
(Iteration 3111 / 4900) loss: 1.385459
(Iteration 3121 / 4900) loss: 1.326855
(Iteration 3131 / 4900) loss: 1.148374
(Iteration 3141 / 4900) loss: 1.223508
(Iteration 3151 / 4900) loss: 1.461523
(Iteration 3161 / 4900) loss: 1.515457
(Iteration 3171 / 4900) loss: 1.557221
(Iteration 3181 / 4900) loss: 1.353831
(Iteration 3191 / 4900) loss: 1.203578
(Iteration 3201 / 4900) loss: 1.281293
(Iteration 3211 / 4900) loss: 1.200816
(Iteration 3221 / 4900) loss: 1.512150
(Iteration 3231 / 4900) loss: 1.580219
(Iteration 3241 / 4900) loss: 1.244586
(Iteration 3251 / 4900) loss: 1.326828
(Iteration 3261 / 4900) loss: 1.337245
(Iteration 3271 / 4900) loss: 1.346274
(Iteration 3281 / 4900) loss: 1.373448
(Iteration 3291 / 4900) loss: 1.311027
(Iteration 3301 / 4900) loss: 1.110510
(Iteration 3311 / 4900) loss: 1.247533
(Iteration 3321 / 4900) loss: 1.353995
(Iteration 3331 / 4900) loss: 1.084901
(Iteration 3341 / 4900) loss: 1.208503
(Iteration 3351 / 4900) loss: 1.306901
(Iteration 3361 / 4900) loss: 1.366972
(Iteration 3371 / 4900) loss: 1.345756
(Iteration 3381 / 4900) loss: 1.343105
(Iteration 3391 / 4900) loss: 1.454141
(Iteration 3401 / 4900) loss: 1.177776
(Iteration 3411 / 4900) loss: 1.400214
(Iteration 3421 / 4900) loss: 1.342663
(Epoch 7 / 10) train acc: 0.547000; val_acc: 0.495000
(Iteration 3431 / 4900) loss: 1.305331
(Iteration 3441 / 4900) loss: 1.325195
(Iteration 3451 / 4900) loss: 1.318475
(Iteration 3461 / 4900) loss: 1.396304
(Iteration 3471 / 4900) loss: 1.360285
(Iteration 3481 / 4900) loss: 1.184701
(Iteration 3491 / 4900) loss: 1.238211
(Iteration 3501 / 4900) loss: 1.283518
(Iteration 3511 / 4900) loss: 1.428018
(Iteration 3521 / 4900) loss: 1.496044
(Iteration 3531 / 4900) loss: 1.381695
(Iteration 3541 / 4900) loss: 1.418340
(Iteration 3551 / 4900) loss: 1.328346
(Iteration 3561 / 4900) loss: 1.322044
(Iteration 3571 / 4900) loss: 1.378151
(Iteration 3581 / 4900) loss: 1.420039
(Iteration 3591 / 4900) loss: 1.219752
(Iteration 3601 / 4900) loss: 1.140046
(Iteration 3611 / 4900) loss: 1.282249
(Iteration 3621 / 4900) loss: 1.390048
(Iteration 3631 / 4900) loss: 1.582304
(Iteration 3641 / 4900) loss: 1.250451
(Iteration 3651 / 4900) loss: 1.328232
(Iteration 3661 / 4900) loss: 1.243136
(Iteration 3671 / 4900) loss: 1.423866
(Iteration 3681 / 4900) loss: 1.340820
(Iteration 3691 / 4900) loss: 1.425670
(Iteration 3701 / 4900) loss: 1.203154
(Iteration 3711 / 4900) loss: 1.249543
(Iteration 3721 / 4900) loss: 1.435793
(Iteration 3731 / 4900) loss: 1.250016
(Iteration 3741 / 4900) loss: 1.319717
(Iteration 3751 / 4900) loss: 1.373801
(Iteration 3761 / 4900) loss: 1.620420
(Iteration 3771 / 4900) loss: 1.321370
(Iteration 3781 / 4900) loss: 1.406195
(Iteration 3791 / 4900) loss: 1.133733
(Iteration 3801 / 4900) loss: 1.477101
(Iteration 3811 / 4900) loss: 1.418692
(Iteration 3821 / 4900) loss: 1.325902
(Iteration 3831 / 4900) loss: 1.274603
(Iteration 3841 / 4900) loss: 1.416265
(Iteration 3851 / 4900) loss: 1.503136
(Iteration 3861 / 4900) loss: 1.323808
(Iteration 3871 / 4900) loss: 1.326465
(Iteration 3881 / 4900) loss: 1.291280
(Iteration 3891 / 4900) loss: 1.643525
(Iteration 3901 / 4900) loss: 1.235655
(Iteration 3911 / 4900) loss: 1.179011
(Epoch 8 / 10) train acc: 0.554000; val_acc: 0.503000
(Iteration 3921 / 4900) loss: 1.136915
(Iteration 3931 / 4900) loss: 1.183221
(Iteration 3941 / 4900) loss: 1.399673
(Iteration 3951 / 4900) loss: 1.311476
(Iteration 3961 / 4900) loss: 1.270733
(Iteration 3971 / 4900) loss: 1.348953
(Iteration 3981 / 4900) loss: 1.154720
(Iteration 3991 / 4900) loss: 1.597530
(Iteration 4001 / 4900) loss: 1.154861
(Iteration 4011 / 4900) loss: 1.382757
(Iteration 4021 / 4900) loss: 1.583512
(Iteration 4031 / 4900) loss: 1.367937
(Iteration 4041 / 4900) loss: 1.432329
(Iteration 4051 / 4900) loss: 1.353527
(Iteration 4061 / 4900) loss: 1.432101
(Iteration 4071 / 4900) loss: 1.348392
(Iteration 4081 / 4900) loss: 1.717534
(Iteration 4091 / 4900) loss: 1.165055
(Iteration 4101 / 4900) loss: 1.191290
(Iteration 4111 / 4900) loss: 1.413249
(Iteration 4121 / 4900) loss: 1.313827
(Iteration 4131 / 4900) loss: 1.309803
(Iteration 4141 / 4900) loss: 1.315864
(Iteration 4151 / 4900) loss: 1.365802
(Iteration 4161 / 4900) loss: 1.554362
(Iteration 4171 / 4900) loss: 1.374609
(Iteration 4181 / 4900) loss: 1.238242
(Iteration 4191 / 4900) loss: 1.169315
(Iteration 4201 / 4900) loss: 1.378836
(Iteration 4211 / 4900) loss: 1.295552
(Iteration 4221 / 4900) loss: 1.416132
(Iteration 4231 / 4900) loss: 1.410366
(Iteration 4241 / 4900) loss: 1.552665
(Iteration 4251 / 4900) loss: 1.123680
(Iteration 4261 / 4900) loss: 1.345930
(Iteration 4271 / 4900) loss: 1.288356
(Iteration 4281 / 4900) loss: 1.394372
(Iteration 4291 / 4900) loss: 1.204953
(Iteration 4301 / 4900) loss: 1.219376
(Iteration 4311 / 4900) loss: 1.372091
(Iteration 4321 / 4900) loss: 1.303272
(Iteration 4331 / 4900) loss: 1.177567
(Iteration 4341 / 4900) loss: 1.269099
(Iteration 4351 / 4900) loss: 1.360113
(Iteration 4361 / 4900) loss: 1.371245
(Iteration 4371 / 4900) loss: 1.221913
(Iteration 4381 / 4900) loss: 1.236036
(Iteration 4391 / 4900) loss: 1.135667
(Iteration 4401 / 4900) loss: 1.302358
(Epoch 9 / 10) train acc: 0.547000; val_acc: 0.477000
(Iteration 4411 / 4900) loss: 1.181607
(Iteration 4421 / 4900) loss: 1.401505
(Iteration 4431 / 4900) loss: 1.292314
(Iteration 4441 / 4900) loss: 1.437959
(Iteration 4451 / 4900) loss: 1.414004
(Iteration 4461 / 4900) loss: 1.262010
(Iteration 4471 / 4900) loss: 1.236764
(Iteration 4481 / 4900) loss: 1.200308
(Iteration 4491 / 4900) loss: 1.269349
(Iteration 4501 / 4900) loss: 1.005077
(Iteration 4511 / 4900) loss: 1.293746
(Iteration 4521 / 4900) loss: 1.340251
(Iteration 4531 / 4900) loss: 1.303106
(Iteration 4541 / 4900) loss: 1.248767
(Iteration 4551 / 4900) loss: 1.320377
(Iteration 4561 / 4900) loss: 1.508266
(Iteration 4571 / 4900) loss: 1.350432
(Iteration 4581 / 4900) loss: 1.281510
(Iteration 4591 / 4900) loss: 1.429621
(Iteration 4601 / 4900) loss: 1.180842
(Iteration 4611 / 4900) loss: 1.075045
(Iteration 4621 / 4900) loss: 1.357894
(Iteration 4631 / 4900) loss: 1.212787
(Iteration 4641 / 4900) loss: 1.512692
(Iteration 4651 / 4900) loss: 1.285667
(Iteration 4661 / 4900) loss: 1.165197
(Iteration 4671 / 4900) loss: 1.293227
(Iteration 4681 / 4900) loss: 1.103044
(Iteration 4691 / 4900) loss: 1.140829
(Iteration 4701 / 4900) loss: 1.389774
(Iteration 4711 / 4900) loss: 1.310982
(Iteration 4721 / 4900) loss: 1.249437
(Iteration 4731 / 4900) loss: 1.216739
(Iteration 4741 / 4900) loss: 1.266213
(Iteration 4751 / 4900) loss: 1.442673
(Iteration 4761 / 4900) loss: 1.219733
(Iteration 4771 / 4900) loss: 1.378369
(Iteration 4781 / 4900) loss: 1.505432
(Iteration 4791 / 4900) loss: 1.232619
(Iteration 4801 / 4900) loss: 1.350596
(Iteration 4811 / 4900) loss: 1.293851
(Iteration 4821 / 4900) loss: 1.317689
(Iteration 4831 / 4900) loss: 1.313958
(Iteration 4841 / 4900) loss: 1.303738
(Iteration 4851 / 4900) loss: 1.320713
(Iteration 4861 / 4900) loss: 1.222695
(Iteration 4871 / 4900) loss: 1.096203
(Iteration 4881 / 4900) loss: 1.234871
(Iteration 4891 / 4900) loss: 1.050064
(Epoch 10 / 10) train acc: 0.525000; val_acc: 0.434000

Tune your hyperparameters

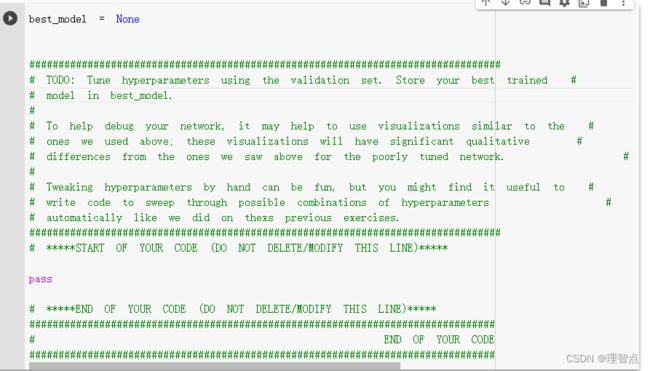
题面

跟之前的差不多，就是找到合适的超参数

代码

best_model = None


#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained  #
# model in best_model.                                                          #
#                                                                               #
# To help debug your network, it may help to use visualizations similar to the  #
# ones we used above; these visualizations will have significant qualitative    #
# differences from the ones we saw above for the poorly tuned network.          #
#                                                                               #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to  #
# write code to sweep through possible combinations of hyperparameters          #
# automatically like we did on thexs previous exercises.                          #
#################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

results = {}
best_val = -1

learning_rates = np.geomspace(3e-4, 3e-2, 3)
regularization_strengths = np.geomspace(1e-6, 1e-2, 5)

import itertools

for lr, reg in itertools.product(learning_rates, regularization_strengths):
    # Create Two Layer Net and train it with Solver
    model = TwoLayerNet(hidden_dim=128, reg=reg)
    solver = Solver(model, data, optim_config={'learning_rate': lr}, num_epochs=10, verbose=False)
    solver.train()
    
    # Compute validation set accuracy and append to the dictionary
    results[(lr, reg)] = solver.best_val_acc

    # Save if validation accuracy is the best
    if results[(lr, reg)] > best_val:
        best_val = results[(lr, reg)]
        best_model = model

# Print out results.
for lr, reg in sorted(results):
    val_accuracy = results[(lr, reg)]
    print('lr %e reg %e val accuracy: %f' % (lr, reg, val_accuracy))

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
#                              END OF YOUR CODE                                #
################################################################################

结果

我跑了24分钟！！！

最后的输出

你可能感兴趣的:(cs231n,python)

理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
一文掌握python面向对象魔术方法（二）程序员neil python python 开发语言
接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
一文掌握python常用的list（列表）操作程序员neil python python 开发语言
目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
python中的深拷贝与浅拷贝 anshejd70787 python
深拷贝和浅拷贝浅拷贝的时候，修改原来的对象，浅拷贝的对象不会发生改变。1、对象的赋值对象的赋值实际上是对象之间的引用：当创建一个对象，然后将这个对象赋值给另外一个变量的时候，python并没有拷贝这个对象，而只是拷贝了这个对象的引用。当对对象做赋值或者是参数传递或者作为返回值的时候，总是传递原始对象的引用，而不是一个副本。如下所示：>>>aList=["kel","abc",123]>>>bLis
用Python实现简单的猜数字游戏程序媛了了 python 游戏 java
猜数字游戏代码：importrandomdefpythonit():a=random.randint(1,100)n=int(input("输入你猜想的数字："))whilen!=a:ifn>a:print("很遗憾，猜大了")n=int(input("请再次输入你猜想的数字："))elifna::如果玩家猜的数字n大于随机数字a，则输出"很遗憾，猜大了"，并提示玩家再次输入。elifn
用Python实现读取统计单词个数程序媛了了 python 游戏 java
完整实例代码：fromcollectionsimportCounterdefpythonit():danci={}withopen("pythonit.txt","r",encoding="utf-8")asf:foriinf:words=i.strip().split()forwordinwords:ifwordnotindanci:danci[word]=1else:danci[word]+=
web前段跨域nginx代理配置刘正强 nginx cms Web
nginx代理配置可参考server部分 server { listen 80; server_name localhost;
spring学习笔记 caoyong spring
一、概述 a>、核心技术 : IOC与AOP b>、开发为什么需要面向接口而不是实现接口降低一个组件与整个系统的藕合程度，当该组件不满足系统需求时，可以很容易的将该组件从系统中替换掉，而不会对整个系统产生大的影响 c>、面向接口编口编程的难点在于如何对接口进行初始化,(使用工厂设计模式)
Eclipse打开workspace提示工作空间不可用 0624chenhong eclipse
做项目的时候，难免会用到整个团队的代码，或者上一任同事创建的workspace， 1.电脑切换账号后，Eclipse打开时，会提示Eclipse对应的目录锁定，无法访问，根据提示，找到对应目录，G:\eclipse\configuration\org.eclipse.osgi\.manager，其中文件.fileTableLock提示被锁定。解决办法，删掉.fileTableLock文件，重
Javascript 面向对面写法的必要性？一炮送你回车库 JavaScript
现在Javascript面向对象的方式来写页面很流行，什么纯javascript的mvc框架都出来了：ember 这是javascript层的mvc框架哦,不是j2ee的mvc框架我想说的是，javascript本来就不是一门面向对象的语言，用它写出来的面向对象的程序，本身就有些别扭，很多人提到js的面向对象首先提的是：复用性。那么我请问你写的js里有多少是可以复用的，用fu
js array对象的迭代方法换个号韩国红果果 array
1.forEach 该方法接受一个函数作为参数，对数组中的每个元素使用该函数 return 语句失效 function square(num) { print(num, num * num); } var nums = [1,2,3,4,5,6,7,8,9,10]; nums.forEach(square); 2.every 该方法接受一个返回值为布尔类型
对Hibernate缓存机制的理解归来朝歌 session 一级缓存对象持久化
在hibernate中session一级缓存机制中，有这么一种情况：问题描述：我需要new一个对象，对它的几个字段赋值，但是有一些属性并没有进行赋值，然后调用 session.save()方法，在提交事务后，会出现这样的情况： 1：在数据库中有默认属性的字段的值为空 2：既然是持久化对象，为什么在最后对象拿不到默认属性的值？通过调试后解决方案如下：对于问题一，如你在数据库里设置了
WebService调用错误合集 darkranger webservice
Java.Lang.NoClassDefFoundError: Org/Apache/Commons/Discovery/Tools/DiscoverSingleton 调用接口出错，一个简单的WebService import org.apache.axis.client.Call;import org.apache.axis.client.Service; 首先必不可
JSP和Servlet的中文乱码处理 aijuans Java Web
JSP和Servlet的中文乱码处理前几天学习了JSP和Servlet中有关中文乱码的一些问题，写成了博客，今天进行更新一下。应该是可以解决日常的乱码问题了。现在作以下总结希望对需要的人有所帮助。我也是刚学，所以有不足之处希望谅解。一、表单提交时出现乱码：在进行表单提交的时候，经常提交一些中文，自然就避免不了出现中文乱码的情况，对于表单来说有两种提交方式：get和post提交方式。所以
面试经典六问 atongyeye 工作面试
题记：因为我不善沟通，所以在面试中经常碰壁，看了网上太多面试宝典，基本上不太靠谱。只好自己总结，并试着根据最近工作情况完成个人答案。以备不时之需。以下是人事了解应聘者情况的最典型的六个问题： 1 简单自我介绍关于这个问题，主要为了弄清两件事，一是了解应聘者的背景，二是应聘者将这些背景信息组织成合适语言的能力。我的回答：(针对技术面试回答，如果是人事面试，可以就掌
contentResolver.query()参数详解百合不是茶 android query()详解
收藏csdn的博客,介绍的比较详细,新手值得一看 1.获取联系人姓名一个简单的例子，这个函数获取设备上所有的联系人ID和联系人NAME。 [java] view plain copy public void fetchAllContacts() {
ora-00054:resource busy and acquire with nowait specified解决方法 bijian1013 oracle 数据库 kill nowait
当某个数据库用户在数据库中插入、更新、删除一个表的数据，或者增加一个表的主键时或者表的索引时，常常会出现ora-00054:resource busy and acquire with nowait specified这样的错误。主要是因为有事务正在执行（或者事务已经被锁），所有导致执行不成功。 1.下面的语句
web 开发乱码征客丶 spring Web
以下前端都是 utf-8 字符集编码一、后台接收 1.1、 get 请求乱码 get 请求中，请求参数在请求头中；乱码解决方法： a、通过在web 服务器中配置编码格式：tomcat 中，在 Connector 中添加URIEncoding="UTF-8"； 1.2、post 请求乱码 post 请求中，请求参数分两部份， 1.2.1、url？参数，
【Spark十六】： Spark SQL第二部分数据源和注册表的几种方式 bit1129 spark
Spark SQL数据源和表的Schema case class apply schema parquet json JSON数据源准备源数据 {"name":"Jack", "age": 12, "addr":{"city":"beijing&
JVM学习之:调优总结 -Xms -Xmx -Xmn -Xss BlueSkator -Xss -Xmn -Xms -Xmx
堆大小设置JVM 中最大堆大小有三方面限制：相关操作系统的数据模型（32-bt还是64-bit）限制；系统的可用虚拟内存限制；系统的可用物理内存限制。32位系统下，一般限制在1.5G~2G；64为操作系统对内存无限制。我在Windows Server 2003 系统，3.5G物理内存，JDK5.0下测试，最大可设置为1478m。典型设置： java -Xmx355
jqGrid 各种参数详解(转帖) BreakingBad jqGrid
jqGrid 各种参数详解分类：源代码分享个人随笔请勿参考解决开发问题 2012-05-09 20:29 84282人阅读评论(22) 收藏举报 jquery 服务器 parameters function ajax string
读《研磨设计模式》-代码笔记-代理模式-Proxy bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ import java.lang.reflect.InvocationHandler; import java.lang.reflect.Method; import java.lang.reflect.Proxy; /* * 下面
应用升级iOS8中遇到的一些问题 chenhbc ios8 升级iOS8
1、很奇怪的问题，登录界面，有一个判断，如果不存在某个值，则跳转到设置界面，ios8之前的系统都可以正常跳转，iOS8中代码已经执行到下一个界面了，但界面并没有跳转过去，而且这个值如果设置过的话，也是可以正常跳转过去的，这个问题纠结了两天多，之前的判断我是在 -(void)viewWillAppear:(BOOL)animated 中写的，最终的解决办法是把判断写在 -(void
工作流与自组织的关系？ comsci 设计模式工作
目前的工作流系统中的节点及其相互之间的连接是事先根据管理的实际需要而绘制好的，这种固定的模式在实际的运用中会受到很多限制，特别是节点之间的依存关系是固定的，节点的处理不考虑到流程整体的运行情况，细节和整体间的关系是脱节的，那么我们提出一个新的观点，一个流程是否可以通过节点的自组织运动来自动生成呢？这种流程有什么实际意义呢？这里有篇论文，摘要是：“针对网格中的服务
Oracle11.2新特性之INSERT提示IGNORE_ROW_ON_DUPKEY_INDEX daizj oracle
insert提示IGNORE_ROW_ON_DUPKEY_INDEX 转自：http://space.itpub.net/18922393/viewspace-752123 在 insert into tablea ...select * from tableb中，如果存在唯一约束，会导致整个insert操作失败。使用IGNORE_ROW_ON_DUPKEY_INDEX提示，会忽略唯一
二叉树:堆 dieslrae 二叉树
这里说的堆其实是一个完全二叉树,每个节点都不小于自己的子节点,不要跟jvm的堆搞混了.由于是完全二叉树,可以用数组来构建.用数组构建树的规则很简单: 一个节点的父节点下标为: (当前下标 - 1)/2 一个节点的左节点下标为: 当前下标 * 2 + 1 &
C语言学习八结构体 dcj3sjt126com c
为什么需要结构体，看代码 # include <stdio.h> struct Student //定义一个学生类型，里面有age, score, sex, 然后可以定义这个类型的变量 { int age; float score; char sex; } int main(void) { struct Student st = {80, 66.6,
centos安装golang dcj3sjt126com centos
#在国内镜像下载二进制包 wget -c http://www.golangtc.com/static/go/go1.4.1.linux-amd64.tar.gz tar -C /usr/local -xzf go1.4.1.linux-amd64.tar.gz #把golang的bin目录加入全局环境变量 cat >>/etc/profile<
10.性能优化-监控-MySQL慢查询 frank1234 性能优化 MySQL慢查询
1.记录慢查询配置 show variables where variable_name like 'slow%' ; --查看默认日志路径查询结果：--不用的机器可能不同 slow_query_log_file=/var/lib/mysql/centos-slow.log 修改mysqld配置文件：/usr /my.cnf[一般在/etc/my.cnf，本机在/user/my.cn
Java父类取得子类类名 happyqing java this 父类子类类名
在继承关系中，不管父类还是子类，这些类里面的this都代表了最终new出来的那个类的实例对象，所以在父类中你可以用this获取到子类的信息！ package com.urthinker.module.test; import org.junit.Test; abstract class BaseDao<T> { public void
Spring3.2新注解@ControllerAdvice jinnianshilongnian @Controller
@ControllerAdvice，是spring3.2提供的新注解，从名字上可以看出大体意思是控制器增强。让我们先看看@ControllerAdvice的实现： @Target(ElementType.TYPE) @Retention(RetentionPolicy.RUNTIME) @Documented @Component public @interface Co
Java spring mvc多数据源配置 liuxihope spring
转自：http://www.itpub.net/thread-1906608-1-1.html 1、首先配置两个数据库 <bean id="dataSourceA" class="org.apache.commons.dbcp.BasicDataSource" destroy-method="close&quo
第12章 Ajax（下） onestopweb Ajax
index.html <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/
BW / Universe Mappings blueoxygen BO
BW Element OLAP Universe Element Cube Dimension Class Charateristic A class with dimension and detail objects (Detail objects for key and desription) Hi
Java开发熟手该当心的11个错误 tomcat_oracle java 多线程工作单元测试
#1、不在属性文件或XML文件中外化配置属性。比如，没有把批处理使用的线程数设置成可在属性文件中配置。你的批处理程序无论在DEV环境中，还是UAT（用户验收测试）环境中，都可以顺畅无阻地运行，但是一旦部署在PROD 上，把它作为多线程程序处理更大的数据集时，就会抛出IOException，原因可能是JDBC驱动版本不同，也可能是#2中讨论的问题。如果线程数目可以在属性文件中配置，那么使它成为
推行国产操作系统的优劣 yananay windows linux 国产操作系统
最近刮起了一股风，就是去“国外货”。从应用程序开始，到基础的系统，数据库，现在已经刮到操作系统了。原因就是“棱镜计划”，使我们终于认识到了国外货的危害，开始重视起了信息安全。操作系统是计算机的灵魂。既然是灵魂，为了信息安全，那我们就自然要使用和推行国货。可是，一味地推行，是否就一定正确呢？先说说信息安全。其实从很早以来大家就在讨论信息安全。很多年以前，就据传某世界级的网络设备制造商生产的交