Leetocde动态规划题目总结(二)

动态规划的概念

Leetcode801使序列递增的最小交换次数

int minSwap(int* nums1, int nums1Size, int* nums2, int nums2Size){
    int n = nums1Size;
    int f[n+1]; //f[i]表示交换了第i个数使得0~i这几个数有序的最小交换次数
    int g[n+1]; //g[i]表示不交换第i个数使得0~i这几个数有序的最小交换次数
    memset(f,0x3f,sizeof(f));
    memset(g,0x3f,sizeof(g));
    f[0] = 1;
    g[0] = 0;
    //题目保证肯定是能排成有序的数组,这就说明了必定有以下两种情况中的一种
    //1.  nums1[i] > nums1[i-1] && nums2[i] > nums2[i-1]
    //2.  nums1[i] > nums2[i-1] && nums2[i] > nums1[i-1]
    for(int i = 1; i < n; i++){
        //用两个if并行主要是可能出现nums1[i]>nums1[i-1]并且nums1[i]>nums2[i-1]的情况
        if(nums1[i] > nums1[i-1] && nums2[i] > nums2[i-1]){
            f[i] = f[i-1] + 1; //此时i i-1这两个位置要么都换,要么都不换
            g[i] = g[i-1];
        }
        if(nums1[i] > nums2[i-1] && nums2[i] > nums1[i-1]){
            f[i] = fmin(g[i-1] + 1,f[i]);
            g[i] = fmin(f[i-1],g[i]);
        }
    }
    return fmin(f[n-1],g[n-1]);
}

买卖股票系列

Leetcode121

只会购买一支股票的情况

int maxProfit(int* prices, int pricesSize){
    int min_price = 0x3f3f3f3f; //记录i天之前的最小的一天的股票值
    int res = 0;
    int n = pricesSize;
    for(int i = 0; i < n; i++){
        min_price = fmin(min_price,prices[i]);
        res = fmax(res,prices[i] - min_price);
    }
    return res;
}

Leetocde122

int maxProfit(int* prices, int pricesSize){
    int n = pricesSize;
    int f[n+1][2];         //f[i][0]表示第i天结尾时，不持有股票时总共获得利润
    memset(f,0,sizeof(0)); //f[i][1]表示第i天结尾时，持有股票时获得的利润
    f[0][0] = 0;
    f[0][1] = -prices[0];
    for(int i = 1; i < n; i++){
        f[i][0] = fmax(f[i-1][0],f[i-1][1]+prices[i]);
        f[i][1] = fmax(f[i-1][1],f[i-1][0] - prices[i]);
    }
    return f[n-1][0];
}

Leetcode123

在买卖股票II的基础上增加了最多只能卖两笔股票的限制，但是这样就可以直接枚举分界点了[0,i] [i+1,n-1]这两段分别求各自买卖股票的结果即可

int maxProfit(int* prices, int n){
    int res = 0;
    for(int i = 0; i < n; i++){//枚举两次股票的分界点
        int min_num = 0x3f3f3f3f;
        int ans_left = 0;
        for(int j = 0; j <= i; j++){
            ans_left = fmax(ans_left,prices[j]-min_num);
            min_num = fmin(prices[j],min_num);
        }
        int min_num_right = 0x3f3f3f3f;
        int ans_right = 0;
        for(int j = i+1;j<n;j++){
            ans_right = fmax(ans_right,prices[j]-min_num_right);
            min_num_right = fmin(min_num_right,prices[j]);
        }
        res = fmax(res,ans_left+ans_right);
    }
    return res;
}

Leetcode188

股票II限制了最多能买2支股票，股票IV限制了最多能够买k支股票

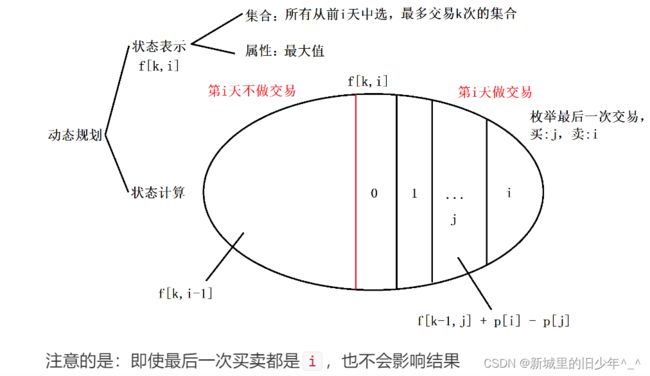
f[k][i]表示前i天中进行k次交易得到的最大利润
然后分为第k天不卖出，即有f[k][i] = f[k][i-1]
第k天卖出,枚举最后一次交易开始的天数，j = 0,1,2,…,i-1
并且最大的交易次数，不会超出总天数的一半，因为每次完整的交易需要两天

int maxProfit(int k, int* prices, int pricesSize){
    int n = pricesSize;
    if(n <= 1) return 0;
    k = fmin(k,n/2); //最大的能够交易的次数不会超过总天数的一半
    int f[k+10][n+10]; //f[k][i]表示i号天及之前天数中交易k次获得的最大利润
    memset(f,0,sizeof(f));
    for(int j = 1; j <= k; j++){
        for(int i = 1; i < n; i++){
            f[j][i] = f[j][i-1]; //第i天没有卖出股票
            for(int t = 0; t <= i; t++){//枚举最后一次买入股票的时间
                f[j][i] = fmax(f[j][i],f[j-1][t]+prices[i]-prices[t]);
            }
        }
    }
    return f[k][n-1];
}

Leetcode309买卖股票含冷冻期

这个题是买卖股票II的基础上，增加了一个冷冻期的限制

int maxProfit(int* prices, int pricesSize){
    int n = pricesSize;
    int f[n+1]; //f[i]表示i号那,卖出股票的最大利润
    int g[n+1]; //g[i]表示i号那天，买入股票的最大利润
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    f[0] = 0;
    g[0] = -prices[0];
    for(int i = 1; i < n; i++){
        f[i] = fmax(f[i-1],g[i-1]+prices[i]);
        if(i>=2) g[i] = fmax(g[i-1],f[i-2]-prices[i]);
        else g[i] = fmax(g[i-1],-prices[i]);
    }
    return f[n-1];
}

Leetcode714买卖股票的最佳时机含手续费

这题和股票II一模一样的思路

int maxProfit(int* prices, int pricesSize, int fee){
    int n = pricesSize;
    int f[n+1]; //f[i]表示i号那天持有股票的最大利润
    int g[n+1]; //g[i]表示i号那天不持有股票的最大利润
    f[0] = -prices[0]-fee;
    g[0] = 0;
    for(int i = 1; i < n; i++){
        f[i] = fmax(f[i-1],g[i-1]-prices[i]-fee);
        g[i] = fmax(g[i-1],f[i-1]+prices[i]);
    }
    return g[n-1];
}

回文串系列

Leetcode647 回文子串

//这个题求所有的回文子串的数，注意这个题的回文子串是连续的
int countSubstrings(char * s){
    int n = strlen(s);
    int res = n;
    for(int i = 0; i < n; i++){
        int l = i - 1, r = i + 1;
        while(l >= 0 && r < n && s[l] == s[r]){
            int len = r - l + 1;
            if(len > 1) res++;
            l--,r++;
        }
        l = i, r = i + 1;
        while(l >= 0 && r < n && s[l] == s[r]){
            int len = r - l + 1;
            if(len > 1) res++;
            l--,r++;
        }
    }
    return res;
}

Leetcode516 最长回文子序列

//这个题求的回文子序列是可以不连续的
int longestPalindromeSubseq(char * s){
    int n = strlen(s);
    int f[n+10][n+10]; //f[i][j]表示s[i~j]这段区间的最大回文子串长度
    memset(f,0,sizeof(f));
    for(int i = 0; i < n; i++) f[i][i] = 1; //每个字符自己构成一个长度为1的回文串
    for(int len = 2; len <= n; len++){
        for(int i = 0; i+len-1 < n; i++){
            int j = i + len - 1;
            f[i][j] = fmax(f[i][j-1],f[i+1][j]); //不从s[i] s[j]这两个端点中更新结果时
            if(s[i] == s[j]) f[i][j] = fmax(f[i+1][j-1] + 2,f[i][j]);
        }
    }
    return f[0][n-1];
}

剑指offerII 94最少回文分割

int minCut(char * s){
    int n = strlen(s);
    int f[n+10];  //f[i]表示把s[0~i]这段分割成回文子串的最小分割次数，显然f[0] = 0
    memset(f,0x3f,sizeof(f));
    f[0] = 0;
    //先预处理判断[i,j]这一段是否是回文串
    bool judge[n+10][n+10]; //判断s[i~j]这一段是不是回文串
    memset(judge,0,sizeof(judge));
    for(int i = 0; i < n; i++) judge[i][i] = true;
    for(int len = 2; len <= n; len++){
        for(int i = 0; i + len - 1 < n; i++){
            int j = i + len - 1;
            if(len == 2) judge[i][j] = s[i] == s[j];
            else judge[i][j] = judge[i+1][j-1] && s[i]==s[j];
        }
    }
    if(judge[0][n-1]) return 0; //本来就是回文串就不需要再分割了
    for(int i = 1; i < n; i++){
        if(judge[0][i]) f[i] = 0;
        else{
            for(int j = 1; j <= i; j++){ //枚举最后被分割的回文串的起始位置
                if(!judge[j][i]) continue;
                f[i] = fmin(f[i],f[j-1]+1);
            }
        }
    }
    return f[n-1];
}

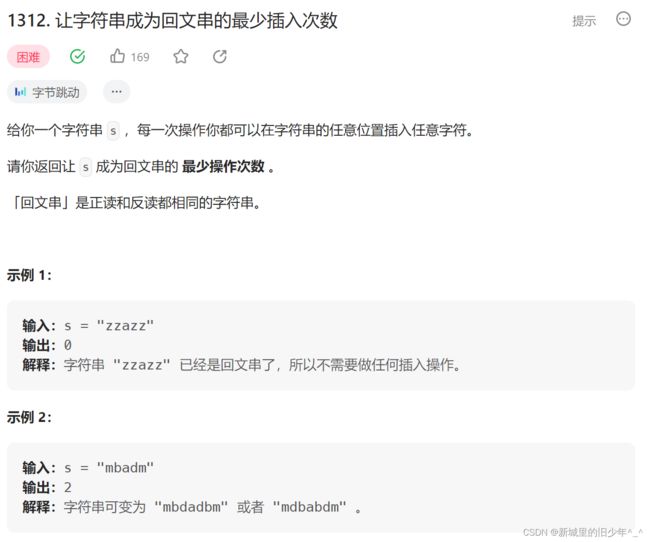
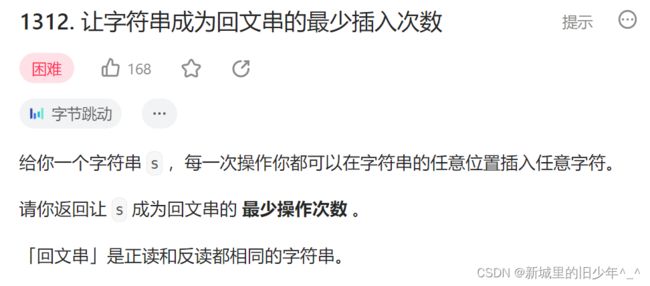
Leetcode1312 让字符串成为回文串的最小插入次数

int minInsertions(char * s){
    int n = strlen(s);
    int f[n+10][n+10];
    memset(f,0,sizeof(f));  //f[i][j]表示[i,j]这个区间的字符串变成回文串需要的最小次数, 总的思想就是枚举回文串长度为1,一直到长度为n
    //长度为1时,肯定有f[i][i] = 0;
    //长度为2时,即f[i][i+1]这种情况需要的次数
    for(int i = 0; i < n - 1; i++){
        if(s[i] != s[i+1]) f[i][i+1] = 1;
    }
    for(int len = 3; len <= n; len++){//此时我们已经有变成长度为2回文串需要的次数了
        for(int i = 0; i + len - 1 < n; i++){
            int j = i + len -1;
            if(s[i] == s[i+len-1]) f[i][j] = f[i+1][j-1];
            else{
                f[i][j] = fmin(f[i+1][j],f[i][j-1]) + 1; //如果不匹配,看长度为len-1的情况,用变成len-1长度的更少的变化次数来进行更新
            }
        }
    }
    return f[0][n-1];

}

Leetcode131 分割回文串I

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

bool ifstr(char * s, int i, int j)//判断是否为回文串
{
    while(i <= j)
    {
        if(s[i] != s[j])
            return false;
        i++;
        j--;
    }
    return true;
}


void dfs(char * s, char *** ans, int * returnSize, int ** returnColumnSizes, int len, char ** path, int path_i,int index)//递归回溯枚举子串
{
   
    if(index >= len)//切割到最后了，保存有效组合
    {
        ans[(*returnSize)] = (char**)malloc(sizeof(char *) * path_i);
        for(int i = 0; i < path_i; i++)
        {
            ans[(*returnSize)][i] = (char *)malloc(sizeof(char) * (len+1));
            strcpy(ans[(*returnSize)][i], path[i]);
        }
        (*returnColumnSizes)[(*returnSize)++] = path_i;
        return;
    }
    for(int i = index; i < len; i++)
    {
        if(ifstr(s, index, i) == false) continue;//剪枝，当前不满足切割条件，就没必要在枚举了
        strncpy(path[path_i], s+index, i-index+1);//满足切割条件，保存子串
        path[path_i][i-index+1] = '\0';
        dfs(s, ans, returnSize, returnColumnSizes, len, path, path_i+1, i+1);//递归重复之前动作
        //其中path_i+1, i+1 都是回溯，因为是实参传个形参，形参不会改变实参的值，所以实际没有变，相等于 i++，再i--
    }
    return;
}

char *** partition(char * s, int* returnSize, int** returnColumnSizes){
    char *** ans = (char ***)malloc(sizeof(int **) * 50000);
    (*returnColumnSizes) = (int *)malloc(sizeof(int) * 50000);
    int len = strlen(s);
    char ** path = (char **)malloc(sizeof(char *) * len);
    for(int i = 0; i < len; i++)
    {
        path[i] = (char *)malloc(sizeof(char) * (len+1));
    }
    *returnSize = 0;//初始化变量
    dfs(s, ans, returnSize, returnColumnSizes,len, path, 0, 0);
    return ans;
}

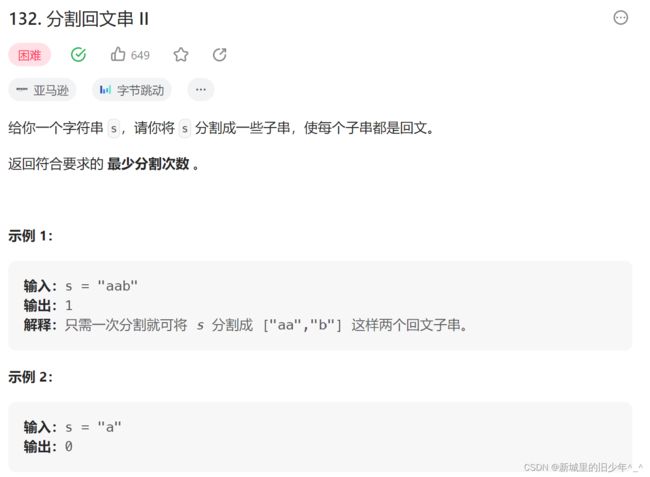
Leetcode132 分割回文串II(同剑指offer94)

int minCut(char * s){
    int n = strlen(s);
    bool check[n+10][n+10];
    memset(check,0,sizeof(check));
    for(int i = 0; i < n; i++) check[i][i] = true;
    for(int len = 2; len <= n; len++){
        for(int i = 0; i + len - 1 < n; i++){
            int j = i + len - 1;
            if(len == 2) check[i][j] = s[i] == s[j];
            else check[i][j] = check[i+1][j-1] && s[i]==s[j];
        }
    }
    int f[n+10];
    memset(f,0x3f,sizeof(f));
    f[0] = 0;
    for(int i = 1; i < n; i++){
        if(check[0][i]) f[i] = 0;
        else{
            for(int j = 1; j <= i; j++){
                if(!check[j][i]) continue;
                f[i] = fmin(f[i],f[j-1]+1);
            }
        }
    }
    
    return f[n-1];
}

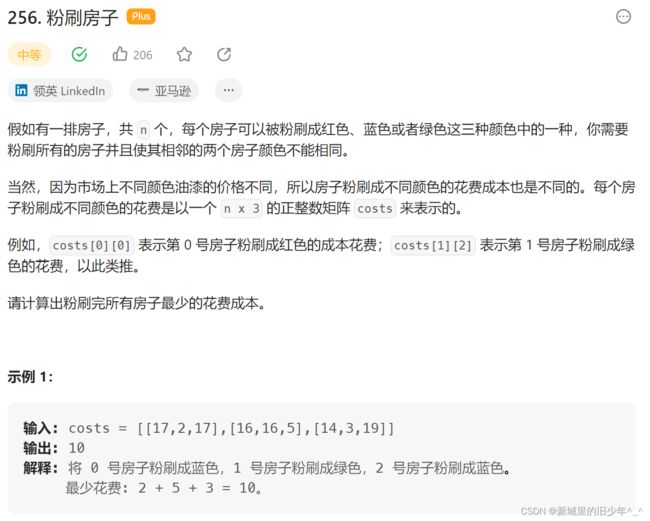
Leetcode256粉刷房子

int minCost(int** costs, int costsSize, int* costsColSize){
    int n = costsSize;
    //f[i][j]表示标号为i的房子被粉刷成颜色j所需要的最小花费
    int f[n+10][5];
    memset(f,0,sizeof(f)); 
    for(int i = 0; i < 3; i++) f[0][i] = costs[0][i]; //0号房子最初可能有三种颜色
    for(int i = 1; i < n; i++){
        f[i][0] = fmin(f[i-1][1],f[i-1][2]) + costs[i][0];
        f[i][1] = fmin(f[i-1][0],f[i-1][2]) + costs[i][1];
        f[i][2] = fmin(f[i-1][0],f[i-1][1]) + costs[i][2];
    }
    return fmin(f[n-1][0],fmin(f[n-1][1],f[n-1][2]));
}

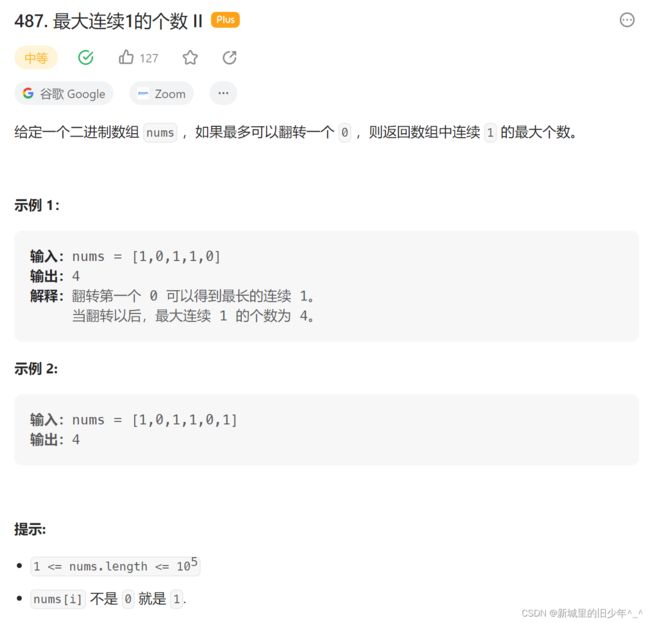
Leetcode487 最大连续1的个数

int findMaxConsecutiveOnes(int* nums, int numsSize){
    int n = numsSize;
    int f[n+1],g[n+1];
    memset(f,0,sizeof(f)); //f[i]表示以nums[i]结尾没有翻转过0的最长连续1 
    memset(g,0,sizeof(g)); //g[i]表示以nums[i]结尾翻转过0的最长连续1
    f[0] = nums[0] == 1;
    g[0] = 1;
    for(int i = 1; i < n; i++){
        if(nums[i] == 1){
            f[i] = f[i-1] + 1;
            g[i] = g[i-1] + 1;
        }
        else{
            f[i] = 0;
            g[i] = f[i-1] + 1;
        }
    }
    int res = 1;
    for(int i = 0; i < n; i++) res = fmax(res,fmax(f[i],g[i]));
    return res;
}

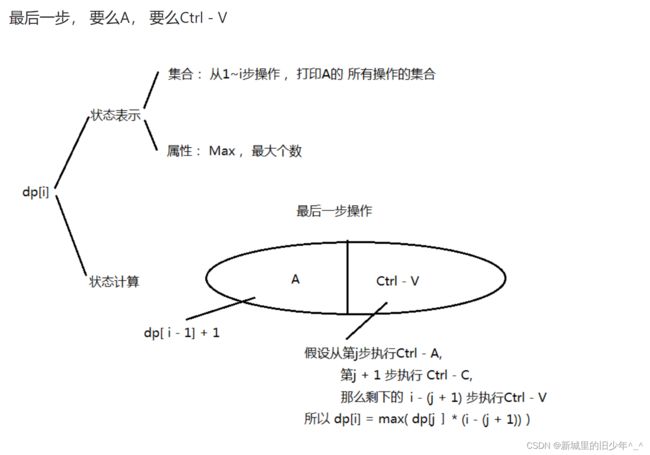
Leetcode651 4键键盘

int maxA(int n){
    int f[n+10]; //f[i]表示操作i次能够在屏幕上输出的A的最大数目
    memset(f,0,sizeof(f));
    f[1] = 1;
    f[2] = 2;
    f[3] = 3;
    for(int i = 4; i <= n; i++){
        //要么添加一个A,要么复制整个空间过来
        f[i] = f[i-1] + 1;
        //假设从第j步执行ctrl-a 第j+1步执行ctrl-c 第j+2 ~ i 步都执行ctrl-v的操作
        for(int j = 1; j + 2 <= i; j++){
            f[i] = fmax(f[i],f[j] * (i-(j+1)));
        }
    }
    return f[n];
}

Leetcode 629逆序对个数

int mod = 1e9 + 7;
int kInversePairs(int n, int k){
    int f[n+1][k+1]; //f[i][j]表示1~i排列形成的数组中，逆序对数量为j的这种数组的个数
    memset(f,0,sizeof(f));
    f[1][0] = 1; //只有[1]这种数组，逆序对数量为0的数组只有1个
    for(int i = 2; i <= n; i++) f[i][0] = 1; //任何一个有i个元素构成的逆序对为0的数组的方案都只有1中
    for(int j = 1; j <= k; j++) f[1][k] = 0; 
    for(int i = 2; i <= n; i++){
        long long sum = 0;
        for(int j=1;j<=k;j++)
            {
                //f[i][j] = f[i-1][0] + f[i-1][1] + ... + f[i-1][j]
                //若第i个数构成i-1个逆序对，那么前i-1个数只能形成0个逆序对
                //若第i个数形成i-2个逆序对，那么前i-1个数只能形成1个逆序对
                //...
                //若第i个数形成0个逆序对，前i-1个数必须形成j个逆序对
                long long sum=0;
                for(int k = j - (i-1); k <= j; k++){//k表示的是前i-1个数需要形成的逆序对数量，再放入i号数后才能形成j个逆序对
                    if(k >= 0) sum += f[i-1][k];
                }
                f[i][j]=sum%mod;
            }

    }
    return f[n][k] % mod;
}

Leetcode646 最长数对链

struct Node{
    int x,y;
}nums[1010];

int cmp(const void* a,const void* b)
{
    struct Node* aa = (struct Node*)a;
    struct Node* bb = (struct Node*)b;
    if(aa->x > bb -> x) return 1;
    return -1;
}

int findLongestChain(int** pairs, int pairsSize, int* pairsColSize){
    int n = pairsSize;
    for(int i = 0; i < n; i++){
        nums[i].x = pairs[i][0];
        nums[i].y = pairs[i][1];
    }
    qsort(nums,n,sizeof(nums[0]),cmp);
    int f[n+10]; //f[i]表示nums[i]结尾的最长数对链
    memset(f,0,sizeof(f));
    f[0] = 1;
    for(int i = 1; i < n; i++){
        f[i] = 1;
        for(int j = 0; j < i; j++){
            if(nums[j].y < nums[i].x) f[i] = fmax(f[i],f[j]+1);
        }
    }
    int res = 1;
    for(int i = 0; i < n; i++) res = fmax(res,f[i]);
    return res;
}

Leetcode673最长递增子序列个数

int findNumberOfLIS(int* nums, int numsSize){
    int n = numsSize;
    int f[n+10]; //f[i]表示以nums[i]结尾的，子序列的最长值
    int g[n+10]; //g[i]表示以nums[i]结尾的最长的子序列个数
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    f[0] = 1; //以nums[0]结尾的子序列的最长值为1
    g[0] = 1; //以nums[0]结尾的最长子序列的个数为1个
    for(int i = 1; i < n; i++){
        f[i] = 1,g[i] = 1;
        for(int j = 0; j < i; j++){
            if(nums[j] < nums[i]){
                if(f[j] + 1 > f[i]){
                    f[i] = f[j] + 1;
                    g[i] = g[j];
                }
                else if(f[j] + 1 == f[i]){
                    g[i] += g[j];
                }
            }
        }
    }
    int res = 0;
    for(int i = 0; i < n; i++) res = fmax(res,f[i]);
    int ans = 0;
    for(int i = 0; i < n; i++){
        if(f[i] == res) ans += g[i];
    }
    return ans;
}

Leetcode678 有效的括号字符串

bool checkValidString(char * s){
    int n = strlen(s);
    bool f[n+10][n+10]; //f[i][j]表示从前i个字符中组合拼接最后是否能剩下的左括号数为j
    memset(f,0,sizeof(f));
    f[0][0] = true; //空字符串能拼出0个左括号
    for(int i = 1; i <= n; i++){
        char c = s[i-1];
        for(int j = 0; j <= i; j++){
            if(c == '('){//如果是左括号，就需要前i-1个字符拼出来的左括号数为j-1
                if(j > 0) f[i][j] = f[i-1][j-1];
                else f[i][j] = false;
            }
            else if(c == ')'){
                f[i][j] = f[i-1][j+1];
            }
            else if(c == '*'){
                f[i][j] = f[i-1][j]; //当*解释为空时
                if(j > 0) f[i][j] |= f[i-1][j-1]; //解释为左括号时
                f[i][j] |= f[i-1][j+1]; //解释为右括号时
            }
        }
    }
    return f[n][0];
}

Leetcode718最长重复数组

int findLength(int* nums1, int nums1Size, int* nums2, int nums2Size){
    int n = nums1Size, m = nums2Size;
    int f[n+1][m+1]; //f[i][j]表示以nums1的第i个数结尾和nums2第j个数结尾的两个序列的最长公共序列
    memset(f,0,sizeof(f));
    int res = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            if(nums1[i-1] == nums2[j-1]) f[i][j] = f[i-1][j-1]+1;
            else f[i][j] = 0;
            res = fmax(res,f[i][j]);
        }
    }
    return res;
}

Leetcode873最长斐波那契子序列长度

方法一：暴力

//枚举开始的两个数，然后开一个哈希表，不断看第三个数能否再哈希表中找到答案
int lenLongestFibSubseq(int* arr, int arrSize){
    long long n = arrSize;
    long long hash[10000000];
    memset(hash,0,sizeof(hash));
    int res = 0; //最长的斐波那契子序列
    for(int i = 0; i < n; i++) hash[arr[i]] = 1;
    for(int i = 0; i < 20; i++) printf("%d ",hash[i]);
    for(int i = 0; i < n; i++){ 
        for(int j = i + 1; j < n; j++){ //枚举起始的两个数
            int a = arr[i], b = arr[j];
            int t = a + b;
            int ans = 0;
            while(hash[t] == 1){
                a = b;
                b = t;
                t = a + b;
                ans++;
            }
            res = fmax(res,ans);
        }
    }
    return res == 0? 0 : res + 2;
}

方法二：动态规划

Leetcode233数字1的个数(数位dp)

Leetcode1012至少有1位重复的数字

相似例题：Leetcode279完全平方数

int numSquares(int n){
    int nums[n+1]; //nums记录那些不超过n的完全平方数
    int cnt = 0;
    for(int i = 1; i <= n; i++){
        if(i*i > n) break;
        nums[cnt++] = i * i;
    }
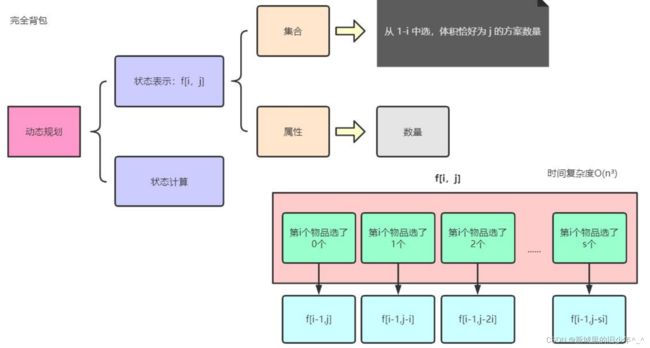
    int f[cnt+1][n+1]; //f[i][j]表示从nums的前i个数中选，最大和为j的使用数最少值
    memset(f,0x3f,sizeof(f));
    for(int i = 0; i <= cnt; i++) f[i][0] = 0;
    for(int i = 1; i <= n; i++) f[0][i] = 0x3f3f3f3f; //从空中选出来组成一个值得选无限多个
    for(int i = 1; i <= cnt; i++){
        for(int j = 1; j <= n; j++){
            f[i][j] = fmin(f[i-1][j],f[i][j]); //不选第i个数
            //f[i][j] = fmin(f[i-1][j] , f[i-1][j-nums[i-1]]+1 , f[i-1][j-2*nums[i-1]]+2 ,...)
            //f[i][j-nums[i-1]] = fmin(f[i-1][j-nums[i-1]],...)
            if(j>=nums[i-1]) f[i][j] = fmin(f[i][j],f[i][j-nums[i-1]]+1);
        }
    }
    return f[cnt][n];
}

模板题: ACwing900整数划分(数位dp)

这个题可以看作是一个完全背包问题来求解

#include 
#include 
#define mod (int)(1e9+7)
int n;

int main()
{
    scanf("%d",&n);
    int f[n+1][n+1]; //f[i][j]表示从前i个数中选，最大和等于j的最大方案数目集合
    memset(f,0,sizeof(f));
    for(int i = 0; i <= n; i++) f[i][0] = 1; //从前i个数中选，和为0的方案只有1种，就是都不选
    for(int j = 1; j <= n; j++) f[0][j] = 0; //从空数中选，值只能是0，只要j>0了，方案数就是0
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            f[i][j] = f[i-1][j]; //第i个数选0个
            //f[i][j] = f[i-1][j] + f[i-1][j-i] + f[i-1][j-2*i] + ...
            //f[i][j-i] = f[i-1][j-i] + f[i-1][j-2*i] + ...
            //所以 f[i][j] = f[i-1][j] + f[i][j-i]
            if(j>=i) f[i][j] = (f[i-1][j] + f[i][j-i])%mod;
        }
    }
    printf("%d",f[n][n]);
    return 0;
}

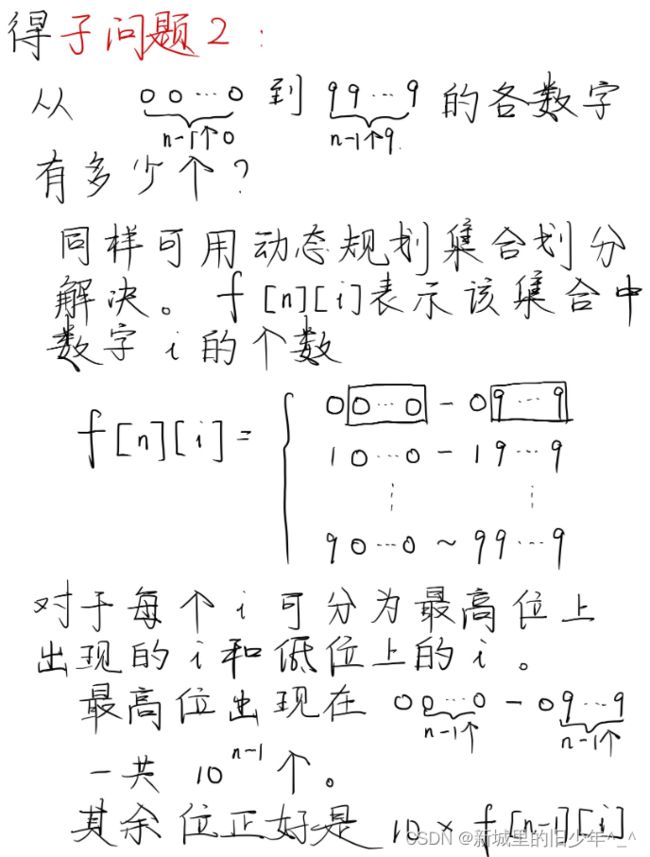
Leetcode902最大为N的数字总和（计数类dp）

模板题: ACwing338计数问题(计数类dp模板)

Leetcode907子数组的最小值之和

//暴力做法,会超时
int mod = 1e9+7;
int sumSubarrayMins(int* arr, int arrSize){
    int res = 0;
    for(int i = 0;i < arrSize; i++){
        int min_num = arr[i];
        for(int j = i; j < arrSize; j++){
            min_num = fmin(min_num,arr[j]);
            res = (res+min_num)%mod;
        }
    }
    return res;
}

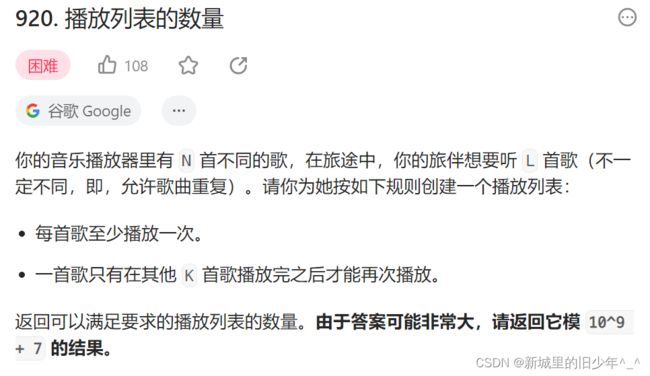
Leetcode920播放列表的数量

Leetcode1312

int minInsertions(char * s){
    int n = strlen(s);
    int f[n+10][n+10];
    memset(f,0,sizeof(f));  //f[i][j]表示[i,j]这个区间的字符串变成回文串需要的最小次数, 总的思想就是枚举回文串长度为1,一直到长度为n
    //长度为1时,肯定有f[i][i] = 0;
    //长度为2时,即f[i][i+1]这种情况需要的次数
    for(int i = 0; i < n - 1; i++){
        if(s[i] != s[i+1]) f[i][i+1] = 1;
    }
    for(int len = 3; len <= n; len++){//此时我们已经有变成长度为2回文串需要的次数了
        for(int i = 0; i + len - 1 < n; i++){
            int j = i + len -1;
            if(s[i] == s[i+len-1]) f[i][j] = f[i+1][j-1];
            else{
                f[i][j] = fmin(f[i+1][j],f[i][j-1]) + 1; //如果不匹配,看长度为len-1的情况,用变成len-1长度的更少的变化次数来进行更新
            }
        }
    }
    return f[0][n-1];

}

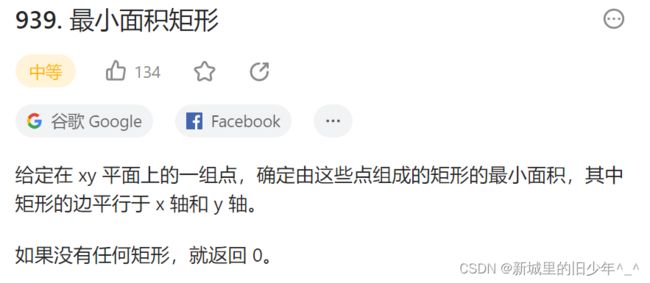
Leetcode939最小的矩形

//总的思路就是枚举所有不同的两个x,y都不同的点,然后构成一个对角线
//通过这两个点再确定剩下的那两个点在不在
bool exist(int** points, int n, int x, int y)
{
    for(int i = 0; i < n; i++){
        if(points[i][0] == x && points[i][1] == y) return true;
    }
    return false;
}

int minAreaRect(int** points, int pointsSize, int* pointsColSize){
    int n = pointsSize;
    int res = 100000000;
    bool flag = false;
    for(int i = 0; i < n; i++)
    {
        for(int j = i + 1; j < n; j++){
            //枚举两个对角线
            int x1 = points[i][0], y1 = points[i][1];
            int x2 = points[j][0], y2 = points[j][1];
            if(x1 != x2 && y1 != y2)
            {
                int area = abs(x1-x2)*abs(y1-y2);
                //如果本身就不可能是答案,直接continue
                if(res <= area) continue;
                //接下来看是不是能够找到(x1,y2)和(x2,y1)这个两个点
                if(exist(points,n,x1,y2) && exist(points,n,x2,y1)){
                    res = fmin(res,area);
                    flag = true;
                }
            }
        }
    }
    if(!flag) return 0;
    return res;
}

Leetcode940不同的子序列II

$f[i][j]$表示从strs的前i个字符中选择,然后以字符 j 结尾的无重复的最大子序列, 值得注意的是, 这里的字符 j 不是 strs[j] 而是 a b c d e … z 中的某一个字符

//char *strcpy(char *dest, const char *src);
//char * strncpy(char *dest, const char *src, size_t n);
#define mod (int)(1e9+7)
int distinctSubseqII(char * str){
    int n = strlen(str);
    char s[n+10];
    s[0] = ' ';
    strcpy(s+1,str);
    int f[n+10][26]; //f[i][j]表示以s的前i个字符中选择,以j号字符结尾的不同字序列
    memset(f,0,sizeof(f));
    for(int i = 0; i < 26; i++) f[0][i] = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 0; j < 26; j++)
        {
            int t = s[i] - 'a';
            if(t != j) f[i][j] = f[i-1][j];
            else{//s[i]-'a'==j时,表示s[i]必选,然后看 前i- 1的总共有多少方案
                int cnt = 1; //前i-1个字符中都不选
                for(int k = 0; k < 26; k++) cnt = (cnt + f[i-1][k])%mod;
                f[i][j] = cnt;
            }
        }
    }
    int res = 0;
    for(int i = 0; i < 26; i++) res = (res + f[n][i])%mod;
    return res;
}

Leetcode983

int mincostTickets(int* days, int daysSize, int* costs, int costsSize){
    int n = daysSize;
    int f[n+10];
    memset(f,0x3f,sizeof(f)); //f[i]表示前i天中的总花费
    f[0] = 0;  //用到了f[0]就得注意初始化,尤其是求最小值的一些题目
    for(int i = 1; i <= n; i++){
        for(int j = i; j >= 1; j--){
            int pre = days[j-1], now = days[i-1];
            if(abs(now-pre) < 1) f[i] = fmin(f[i],f[j-1]+costs[0]); //相差小于1天, i的花费能被days[j-1]这天的花费覆盖
            if(abs(now-pre) < 7) f[i] = fmin(f[i],f[j-1]+costs[1]);
            if(abs(now-pre) <30) f[i] = fmin(f[i],f[j-1]+costs[2]);
            if(abs(now-pre)>=30) break;  //超过30天,不可能被更新了
        }
    }
    return f[n];
}

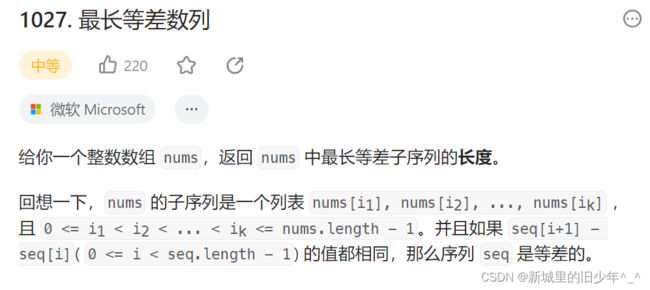
Leetcode1027

int longestArithSeqLength(int* nums, int numsSize){
    int n = numsSize;
    int f[1010][1010]; //f[i][d]表示以第i个数结尾的公差为d的最大子序列长度
    int res = 0;
    for(int i = 0; i < 1010; i++){
        for(int j = 0; j < 1010; j++) f[i][j] = 1;  //每个数都至少自己形成一个等差数列
    }
    for(int i = 1; i <= n; i++){
        for(int j = 1; j < i; j++){
            f[i][j] = fmax(1,f[i][j]);
            int d = nums[i-1] - nums[j-1] + 500; //因为公差可能是负数,所以得加偏移
            f[i][d] = fmax(f[i][d],f[j][d]+1);
            res = fmax(res, f[i][d]);
        }
    }
    return res;
}

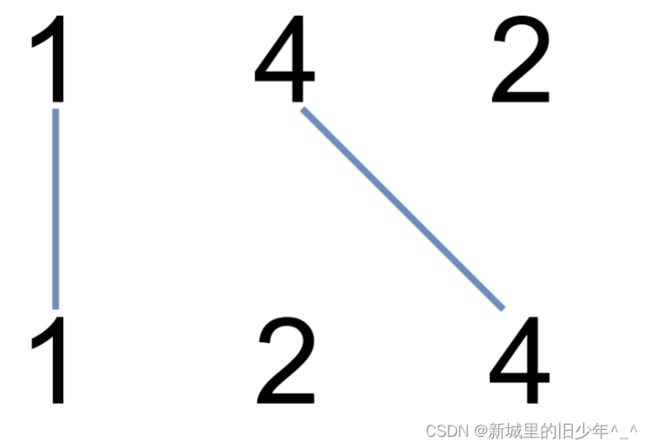
Leetcode1035不相交的线

int maxUncrossedLines(int* nums1, int nums1Size, int* nums2, int nums2Size){
    int n = nums1Size, m = nums2Size;
    int f[1100][1100];
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            f[i][j] = fmax(f[i-1][j],f[i][j-1]);
            if(nums1[i-1] == nums2[j-1]) f[i][j] = fmax(f[i][j],f[i-1][j-1]+1);
        }
    }    
    return f[n][m];
}

Leetcode1048最长字符串链

//对于字符串长度排序,可以把字符串放到结构体中,然后按照结构体排序的方法来对字符串数组进行排序
struct str{
    char s[20];
    int len;
}strs[1010];

int cmp(const void * a, const void * b)
{
    struct str* aa = (struct str*)a;
    struct str* bb = (struct str*)b;
    if(aa->len > bb->len) return 1;
    return -1;
}

bool if_pre(char* s1,char* s2)//判断s1是否是s2的前身
{
    int n = strlen(s1), m = strlen(s2);
    if(n > m) return false;
    // if((m-n) > 1) return false; 这么写有的用例过不了...
    
    if((m-n) != 1) return false; //相差长度不是1肯定不是前身
    //前身只比当前字符串长度少1,然后是当前字符串的一个长度为m-1的子序列
    int i = 0, j = 0;
    while(i < n && j < m)
    {
        if(s1[i] == s2[j]) i++,j++;
        else j++;
    }
    if(i == n) return true;
    return false;
}


int longestStrChain(char ** words, int wordsSize){
    int n = wordsSize;
    for(int i = 0; i < n; i++){ 
        strcpy(strs[i].s,words[i]);
        strs[i].len = strlen(words[i]);
    }
    qsort(strs,n,sizeof(strs[0]),cmp);
    for(int i = 0; i < n; i++) printf("%s %d\n",strs[i].s,strs[i].len);
    int f[n+10]; //f[i]表示所有以strs[i]结尾的最长前身序列数
    for(int i = 0; i < n; i++) f[i] = 1;
    for(int i = 1; i < n; i++){
        for(int j = i-1; j >= 0; j--){
            if(if_pre(strs[j].s,strs[i].s)){
                f[i] = fmax(f[i],f[j]+1);
            }
        }
    }
    int res = 0;
    for(int i = 0; i < n; i++) res = fmax(res,f[i]);
    return res;
}

LeetCode1049最后一块石头重量

//总的思路就是把石头分成两部分, 使得这两部分差值尽可能小
//然后这题转成了个01背包
int lastStoneWeightII(int* stones, int stonesSize){
    int sum = 0, n = stonesSize;
    for(int i = 0; i < stonesSize; i++) sum += stones[i];
    int m = sum / 2;
    int f[n+10][m+10]; //f[i][j]表示从前i个物品选,总重量不超过j的最大重量集合
    memset(f,0,sizeof(f));
    for(int i = 1; i <= n; i++){
        for(int j = 0; j <= m; j++){
            f[i][j] = f[i-1][j];
            if(j >= stones[i-1]) f[i][j] = fmax(f[i-1][j],f[i-1][j-stones[i-1]]+stones[i-1]);
        }
    }
    int a = f[n][m], b = sum - a;
    printf("%d",a);
    return abs(a-b);
}

Leetcode1062 最长重复子串

通过这道题最简单的做法是动态规划，状态定义为dp[i][j]是两个分别以i和j结尾的相同子串的最大长度，其中i永远小于j。所有状态的值均初始化为0，状态转移时，如果s[i]和s[j]不同就不必管，因为以i结尾和以j结尾不会是相同子串，如果s[i]和s[j]相同，那么dp[i][j]就等于dp[i-1][j-1]+1，这点应该是很显然的，就是给i-1和j-1结尾的重复子串两边各加了一个相同字符。注意此时如果i=0，那么dp[i][j]就是1。

int longestRepeatingSubstring(char * s){
    int n = strlen(s);
    int f[n+10][n+10];
    memset(f,0,sizeof(f)); //f[i][j]表示以s[i-1]和s[j-1]结尾的两个相同子串的最大长度
    f[0][0] = 1; //表示空串和空串相同
    for(int i = 1; i <= n; i++){
        for(int j = i + 1; j <= n; j++){
            if(s[i-1] == s[j-1]) f[i][j] = f[i-1][j-1] + 1;
            else f[i][j] = 0;
        }
    }
    int res = 0;
    for(int i = 1; i <= n; i++){
        for(int j = i + 1; j <= n; j++) res = fmax(res,f[i][j]);
    }
    return res;
}

Leetcode1092最短公共超序列

如果是只求长度，那么就是先求一下两个串的最长公共子序列t, 然后用第一个串的不在公共序列里的长度和第二个串的不爱公共序列里的长度加进来即可

//只求长度的版本
char * shortestCommonSupersequence(char * str1, char * str2){
    int n = strlen(str1), m = strlen(str2);
    int f[n+1][m+1]; //求最长公共子序列
    memset(f,0,sizeof(f));
    for(int i = 1; i <= n; i++){
        for(int j = 1; j<= m; j++){
            f[i][j] = fmax(f[i-1][j],f[i][j-1]);
            if(str1[i-1] == str2[j-1]) f[i][j] = fmax(f[i][j],f[i-1][j-1]+1);
        }
    }
    int res = f[n][m] + (n-f[n][m]) + (m-f[n][m]);
    printf("%d",res);
    return NULL;
}

Leetcode1162地图分析

这个题就是求出所有海洋到陆地的最短路,然后在这些最短路中输出一个最长的

int maxDistance(int** grid, int gridSize, int* gridColSize){
    //找到每个点到陆地的最短距离,然后返回所有最短距离中最大的长度
    int n = gridSize, m = *gridColSize;
    //如果全是海洋或者陆地返回-1
    int visit[2];
    memset(visit,0,sizeof(visit));
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j]) visit[1] = 1;
            else visit[0] = 1;
        }
    }
    if(!(visit[0]&&visit[1])) return -1;

    int f[n+10][m+10]; //f[i][j]表示(i,j)这个点到陆地的最短距离
    int g[n+10][m+10]; //f[i][j]是从左上角开始出发得到的最短路,g[i][j]是从右下角出发得到的到陆地的最短路
    memset(f,0x3f,sizeof(f));
    memset(g,0x3f,sizeof(g));
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j]) f[i][j] = 0,g[i][j] = 0;; //陆地本身的距离是0
        }
    }
    //对于(i,j)这个点要么是从左上角过来,要么是从右下角过来
    //考虑从左上角过来的情况
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j]) continue;
            if(i-1>=0) f[i][j] = fmin(f[i][j],f[i-1][j]+1);
            if(j-1>=0) f[i][j] = fmin(f[i][j],f[i][j-1]+1);
        }
    }
    for(int i = n - 1; i >= 0; i--){
        for(int j = m - 1; j >= 0; j--)
        {
            if(grid[i][j]) continue;
            if(i+1 < n) g[i][j] = fmin(g[i][j],g[i+1][j]+1);
            if(j+1 < m) g[i][j] = fmin(g[i][j],g[i][j+1]+1);
        }
    }
    int res = -1;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j]) continue;
            int t = fmin(f[i][j],g[i][j]);
            res = fmax(res,t);
        }
    }
    return res;
}

Leetcode1186

int maximumSum(int* arr, int arrSize){
    int n = arrSize;
    int f[n+10]; //f[i]表示没有删除过元素的子数组的最大和
    int g[n+10]; //g[i]表示删除过元素的子数组的最大和
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    f[0] = arr[0];
    g[0] = -1000000;
    for(int i = 1; i < n; i++){
        f[i] = fmax(f[i-1]+arr[i],arr[i]);
        g[i] = fmax(g[i-1]+arr[i],f[i-1]);
    }
    int res = -1000000;
    for(int i = 0; i < n;i++){
        int t = fmax(f[i],g[i]);
        res = fmax(res,t);
    }
    return res;
}

Leetcode152

//nums中有负数，如果当前是个负数的话，我们希望之前的乘积极可能小，才可能乘出更大的乘积
int maxProduct(int* nums, int numsSize){
    int n = numsSize;
    int f[n+10]; //以i结尾的乘积最大的子序列乘积值
    int g[n+10]; //以i结尾的乘积最小的子序列乘积值
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    f[0] = nums[0];
    g[0] = nums[0];
    for(int i = 1; i < n; i++){
        if(nums[i] > 0){
            f[i] = fmax(nums[i],f[i-1]*nums[i]);
            g[i] = fmin(nums[i],g[i-1]*nums[i]);
        }
        else if(nums[i] == 0){
            f[i] = g[i] = 0;
        }
        else{
            f[i] = fmax(nums[i],g[i-1]*nums[i]);
            g[i] = fmin(nums[i],f[i-1]*nums[i]);
        }
    }
    int res = -10000000;
    for(int i = 0; i < n; i++) res = fmax(res,f[i]);
    return res;
}

Leetcode1220

int countVowelPermutation(int n){
    int mod = 1e9 + 7;
    int f[n+10][6]; //f[i][j]表示第i个字母以j号字母结尾形成的字符串构成的最大种类
    memset(f,0,sizeof(f));
    for(int i = 0; i < 5; i++) f[0][i] = 1; //长度为1时，每种结尾都只有1中可能性
    for(int i = 1; i < n; i++){
        f[i][0] = ((f[i-1][1] + f[i-1][2])%mod +f[i-1][4])%mod; //i号位置是a时，i-1号位置可以是e i u
        f[i][1] = (f[i-1][0] + f[i-1][2])%mod;
        f[i][2] = (f[i-1][1] + f[i-1][3])%mod;
        f[i][3] = f[i-1][2];
        f[i][4] = (f[i-1][2] + f[i-1][3])%mod;
    }
    int res = 0;
    for(int i = 0; i < 5; i++) res = (res + f[n-1][i])%mod;
    return res;
}

Leetcode1235 规划找兼职工作

//时间复杂度O(n^2)，超时，需要优化一下
struct Job{
    int start;
    int end;
    int val;
}job[100100];

int cmp(const void* a,const void* b)
{
    struct Job* aa = (struct Job*) a;
    struct Job* bb = (struct Job*) b;
    if(aa->end > bb->end) return 1;
    return -1;
}

int jobScheduling(int* startTime, int startTimeSize, int* endTime, int endTimeSize, int* profit, int profitSize){
    int n = startTimeSize;
    for(int i = 0; i < n; i++){
        job[i].start = startTime[i];
        job[i].end = endTime[i];
        job[i].val = profit[i];
    }
    int f[n+10]; //f[i]表示前i个工作中，选出来的最大利益方案，那么就分为了选第i个工作和不选第i个工作
    memset(f,0,sizeof(f));
    qsort(job,n,sizeof(job[0]),cmp);
    f[0] = job[0].val;
    for(int i = 1; i < n; i++){
        f[i] = fmax(job[i].val,f[i-1]); //不选第i个工作时，答案是从前i-1中选, 或者只选自己，不选之前的工作
        for(int j = i - 1; j >= 0; j--){
            if(job[j].end <= job[i].start) f[i] = fmax(f[i],f[j] + job[i].val);
        }
    }
    for(int i = 0; i < n; i++) printf("%d %d %d\n",job[i].start,job[i].end,job[i].val);
    for(int i = 0; i < n; i++) printf("%d ",f[i]);
    return f[n-1];
}

//二分优化
struct Job{
    int start;
    int end;
    int val;
}job[100100];

int cmp(const void* a,const void* b)
{
    struct Job* aa = (struct Job*) a;
    struct Job* bb = (struct Job*) b;
    if(aa->end > bb->end) return 1;
    return -1;
}

int jobScheduling(int* startTime, int startTimeSize, int* endTime, int endTimeSize, int* profit, int profitSize){
    int n = startTimeSize;
    for(int i = 0; i < n; i++){
        job[i].start = startTime[i];
        job[i].end = endTime[i];
        job[i].val = profit[i];
    }
    int f[n+10]; //f[i]表示前i个工作中，选出来的最大利益方案，那么就分为了选第i个工作和不选第i个工作
    memset(f,0,sizeof(f));
    qsort(job,n,sizeof(job[0]),cmp);
    f[0] = job[0].val;
    for(int i = 1; i < n; i++){
        f[i] = fmax(job[i].val,f[i-1]); //不选第i个工作时，答案是从前i-1中选, 或者只选自己，不选之前的工作
        // for(int j = i - 1; j >= 0; j--){
        //     if(job[j].end <= job[i].start) f[i] = fmax(f[i],f[j] + job[i].val);
        // }
        int l = 0, r = i - 1, target = job[i].start;
        while(l < r){
            int mid = (l+r+1)/2;
            if(job[mid].end <= target) l = mid; 
            else r = mid - 1;
        }
        if(job[l].end <= target)  f[i] = fmax(f[i],f[l] + job[i].val);
    }
    for(int i = 0; i < n; i++) printf("%d %d %d\n",job[i].start,job[i].end,job[i].val);
    for(int i = 0; i < n; i++) printf("%d ",f[i]);
    return f[n-1];
}

Leetcode 1262可被3整除的最大和

int maxSumDivThree(int* nums, int numsSize){
    int n = numsSize;
    if(n == 1){
        if(nums[0]%3 == 0) return nums[0];
        return 0;
    }
    int f[n+10][3]; //f[i][j]表示从0~i中选出，最大和语余0，余1，余2的几种情况
    memset(f,0,sizeof(f));
    int t = nums[0]%3;
    if(t == 0) f[0][0] = nums[0],f[0][1] = -10000, f[0][2] = -100000; //不存在的话设为一个不可能的值让他不被更新即可
    else if(t == 1) f[0][1] = nums[0], f[0][0] = -10000, f[0][2] = -100000;
    else if(t == 2) f[0][2] = nums[0], f[0][0] = -10000, f[0][1] = -100000;
    for(int i = 1; i < n; i++){
        int temp = nums[i] % 3;
        if(temp == 0){
            f[i][0] = fmax(fmax(f[i-1][0],f[i-1][0] + nums[i]),nums[i]); //不选i号，那么从前i-1中选， 选了i号,那么之前i-1中选出来的和余数也得是0
            f[i][1] = fmax(f[i-1][1],f[i-1][1] + nums[i]);
            f[i][2] = fmax(f[i-1][2],f[i-1][2] + nums[i]);
        }
        else if(temp == 1){
            f[i][0] = fmax(f[i-1][0],f[i-1][2] + nums[i]);
            f[i][1] = fmax(fmax(f[i-1][1],f[i-1][0] + nums[i]),nums[i]);
            f[i][2] = fmax(f[i-1][2],f[i-1][1] + nums[i]);
        }
        else if(temp == 2){
            f[i][0] = fmax(f[i-1][0],f[i-1][1] + nums[i]);
            f[i][1] = fmax(f[i-1][1],f[i-1][2] + nums[i]);
            f[i][2] = fmax(fmax(f[i-1][2],f[i-1][0] + nums[i]),nums[i]);
        }
    }
    printf("0 1 2\n\n");
    for(int i = 0; i < n; i++) printf("%d:  %d %d %d\n",nums[i],f[i][0],f[i][1],f[i][2]);
    return f[n-1][0];
}

Leetcode1269

#define mod (int)(1e9+7)
int numWays(int steps, int arrLen){
    long long n = steps, m = fmin(arrLen,steps);  //因为是从0开始走，所以数组过长时其实没必要，并且测试数据会越界
    if(m == 1) return 1;
    int f[n+1][m+1]; //f[i][j]表示走了i部来到位置j的最大方案数
    memset(f,0,sizeof(f));
    f[0][0] = 1;
    for(int i = 1; i<= n; i++){
        f[i][0] = (f[i-1][0] + f[i-1][1])%mod; //若在位置0，那么上一步位置得在位置0或者位置1
        f[i][m-1] = (f[i-1][m-2] + f[i-1][m-1]) % mod;
        for(int j = 1; j < m - 1; j++){
            f[i][j] = ((f[i-1][j] + f[i-1][j-1])%mod + f[i-1][j+1])%mod;
        }
    }
    return f[n][0];
}

Leetcode1277

暴力

//暴力O(n^3)超时
int res;
bool valid(int** matrix,int x,int y,int len,int n,int m)
{
    if(x + len - 1 >= n) return false;
    if(y + len - 1 >= m) return false;
    for(int i = 0; i < len; i++){
        for(int j = 0; j < len; j++){
            if(matrix[x + i][y + j] != 1) return false;
        }
    }
    return true;
}

int countSquares(int** matrix, int matrixSize, int* matrixColSize){
    int n = matrixSize, m = *matrixColSize;
    res = 0;
    for(int x = 0; x < n; x++){
        for(int y = 0; y < m; y++){
            for(int len = fmin(n-x,m-y);len;len--){
                printf("x=%d y=%d len=%d valid=%d\n",x,y,len,valid(matrix,x,y,len,n,m));
                if(valid(matrix,x,y,len,n,m)) res++;
            }
        }
    }
    return res;
}

DP法

int countSquares(int** matrix, int matrixSize, int* matrixColSize){
    int n = matrixSize, m = *matrixColSize;
    int f[n+10][m+10]; //f[i][j]表示以(i,j)作为正方形右下角结尾的正方形的最大边长，同时这个最大边长也是数目
    for(int i = 0; i < n; i++) f[i][0] = matrix[i][0];
    for(int i = 0; i < m; i++) f[0][i] = matrix[0][i];
    for(int i = 1; i < n; i++){
        for(int j = 1; j < m; j++){
            if(!matrix[i][j]){
                f[i][j] = 0;
                continue;
            }
            f[i][j] = fmin(fmin(f[i-1][j],f[i][j-1]),f[i-1][j-1])+1;
        }
    }
    int res = 0;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++) res += f[i][j];
    }
    return res;
}

相似例题：

int maximalSquare(char** matrix, int matrixSize, int* matrixColSize){
    int n = matrixSize, m = *matrixColSize;
    int f[n+10][m+10]; //f[i][j]表示以(i,j)作为右下角结尾的正方形的最大边长
    memset(f,0,sizeof(f));
    for(int i = 0; i < n; i++) f[i][0] = matrix[i][0] - '0';
    for(int i = 0; i < m; i++) f[0][i] = matrix[0][i] - '0';
    for(int i = 1; i < n; i++){
        for(int j = 1; j < m; j++){
            if(matrix[i][j] == '0'){
                f[i][j] = 0;
                continue;
            }
            f[i][j] = fmin(fmin(f[i-1][j],f[i][j-1]),f[i-1][j-1]) + 1;
        }
    }
    int res = 0;
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            res = fmax(res, f[i][j]*f[i][j]);
        }
    }
    return res;
}

Leetcode1326

//这个题可以转化为Leetcode1024视频剪辑的模板来做
struct Node{
    int start,end;
}node[10100];

int cmp(const void *a , const void *b)
{
    struct Node* aa = (struct Node*)a;
    struct Node* bb = (struct Node*)b;
    if(aa->start > bb->end) return 1;
    return -1;
}

int minTaps(int n, int* ranges, int rangesSize){
    int m = rangesSize;
    for(int i = 0; i <= n; i++){ //表示每个水龙头灌溉的范围，用区间来进行表示
        node[i].start = (i-ranges[i]) < 0 ? 0 : i-ranges[i];
        node[i].end = (i+ranges[i]) > n ? n : i + ranges[i]; 
    }
    qsort(node,n+1,sizeof(node[0]),cmp);
    int f[n+10];  //f[i]表示[0,i]区间被覆盖需要的最小数目
    memset(f,0x3f,sizeof(f));
    f[0] = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 0; j <= n; j++){
            int start = node[j].start, end = node[j].end;
            if(start <= i && end >= i) f[i] = fmin(f[i],f[start]+1);
        }
    }
    for(int i = 0;i <= n; i++) printf("%d ",f[i]);
    return f[n] > 1000000 ? -1 : f[n];
}

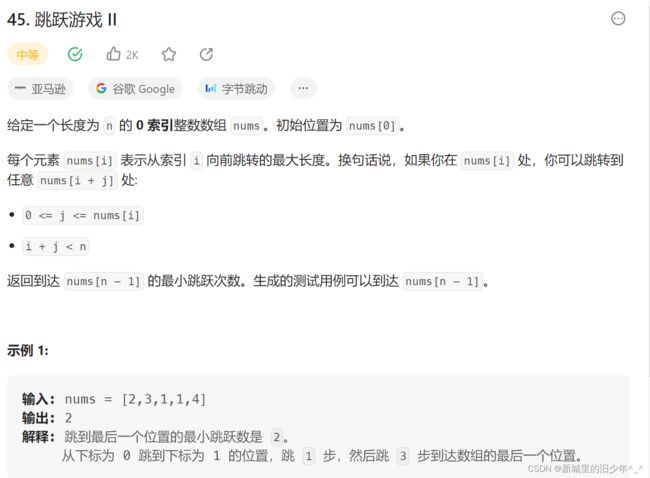
相似题目：Leetcode45跳跃游戏II

int jump(int* nums, int numsSize){
    int n = numsSize;
    int f[n+10]; //f[i]表示跳到i号位置，需要的最小步数
    memset(f,0x3f,sizeof(f));  //求最小值一定要记得初始化为一个大数！
    f[0] = 0;
    for(int i = 1; i < n; i++){
        for(int j = 0; j < i; j++){
            if(j + nums[j] >= i) f[i] = fmin(f[i],f[j]+1);
        }
    }
    for(int i = 0; i < n; i++) printf("%d ",f[i]);
    return f[n-1];
}

相似题目: Leetcode1024视频拼接

struct Node{
    int start,end;
}node[110];

int cmp(const void* a,const void* b)
{
    struct Node* aa = (struct Node*)a;
    struct Node* bb = (struct Node*)b;
    if(aa->start > bb->start) return 1;
    return -1;
}

int videoStitching(int** clips, int clipsSize, int* clipsColSize, int time){
    int n = time, m = clipsSize;
    for(int i = 0; i < m; i++){
        node[i].start = clips[i][0];
        node[i].end = clips[i][1];
    }
    qsort(node,m,sizeof(node[0]),cmp);
    int f[n+10];  //f[i]表示区间[0,i]被覆盖需要的剪辑段最小数目
    memset(f,0x3f,sizeof(f));
    f[0] = 0; //[0,0]这个段被覆盖，不需要剪辑段即可覆盖
    for(int i = 1; i <= n; i++){
        for(int j = 0; j < m; j++)
        {
            int left = node[j].start, right = node[j].end;
            if(left <= i && right >= i){  //如果这个区间能覆盖掉后半段[left,i]那么由[0,left]这部分转移
                f[i] = fmin(f[i],f[left]+1);
            }
        }
    }
    return f[n] > 100000 ? -1:f[n];
}

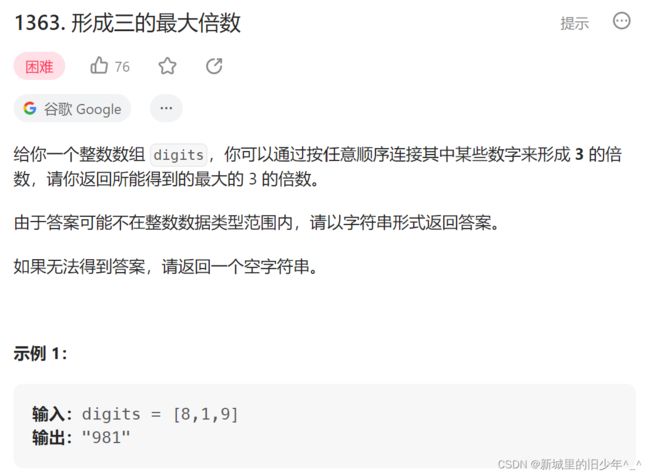
Leetcode1363形成3的最大倍数

//f[i][j]表示从前i个数中选，余数为j的最长的数长度，这个最长的数长度也是最大的数
//设前i-1个数选出的余数为d1, 前i个数选出的数余数为d2
// d1 d2 需要满足这个关系：
// 根据digits[i-1]%3的结果来进行判断
// (d1 + digits[i-1]%3)%3 = d2
// 如果有A=(B-C)%D，那么B=(A+C)%D
// 然后为了保证一定是正数 d1 = (d2 + 3 + digits[i-1]%3)%mod

int cmp(const void* a,const void* b) //先把digits从小到大排序
{
    return *(int*)a - *(int*)b;
}
char * largestMultipleOfThree(int* digits, int digitsSize){
    int n = digitsSize;
    qsort(digits,n,sizeof(digits[0]),cmp);
    int f[n+1][3];
    memset(f,0,sizeof(f));
    f[0][1] = f[0][2] = -0xffff; //这里得初始化为一个较小的数
    for(int i = 1; i <= n; i++){
        for(int j = 0; j < 3; j++){
            f[i][j] = fmax(f[i-1][j], f[i-1][(j + 3 - digits[i-1]%3)%3]+1); //选第i个数和不选第i个数
            //选digits[i-1]时的余数j 是由前i-1个数选出来余数为 (j + 3 - digits[i-1]%3)%3这个数转移过来的
        }
    }
    printf("%d",f[n][0]);
    char* res = malloc(sizeof(char)*10010);
    int cnt = 0;
    for(int i = n, j = 0; i; i--){
        int pre_j = (j + 3 - digits[i-1]%3)%3;
        if(f[i][j] == f[i-1][pre_j]+1){
            res[cnt++] = '0' + digits[i-1];
            j = pre_j;
        }
    }
    res[cnt] = '\0';
    if(res[0] == '0'){
        return "0";
    }
    return res;
}

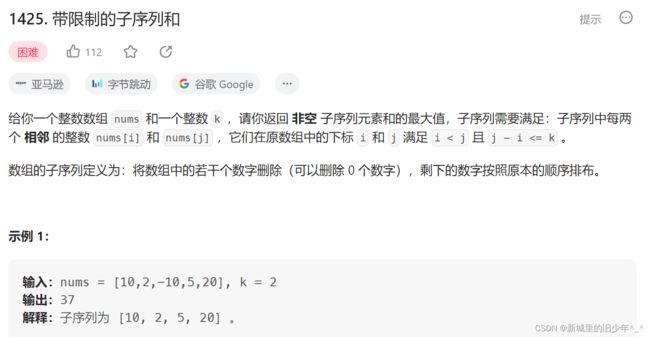
Leetcode1425

int constrainedSubsetSum(int* nums, int numsSize, int k){
    int n = numsSize;
    int f[n+1];  //f[i]表示以i号点结尾的有限制的最大和
    memset(f,0,sizeof(f));
    f[0] = nums[0];
    for(int i = 1; i < n; i++){
        f[i] = nums[i];
        for(int j = i-1;j>=fmax(0,i-k);j--){
            f[i] = fmax(f[i],f[j]+nums[i]); //从[i-k,j]中找一个最大的f[j]
        }
    }
    int res = -0x3f3f3f3f;
    for(int i = 0; i <n; i++){
        printf("%d ",f[i]);
        res = fmax(res,f[i]);
    }
    return res;
}

Leetcode1477

这个题的一个子数组是连续的几个数，所以可以用前缀和来找子数组的值，并且由于这个题目中所有数都是正数，因此我们可以用双指针的思想来进一步优化求子数组的target

Leetcode1653 使字符串平衡的最小删除次数

如图所示，我们给每一个空隙一个编号，假设有n个节点，那么空隙的编号就是 0 1 2 … n-1 n

//这个题就是b不能在a的前面，就是问我们怎么删除能使得变成aaa..bb..的形式
int minimumDeletions(char * s){
    int n = strlen(s);
    int leftb[n+10];   //leftb[i]记录i号空隙左边总共的b的数目
    int righta[n+10];  //righta[i]表示i号空隙右边a的数目
    memset(leftb,0,sizeof(leftb));
    memset(righta,0,sizeof(righta));
    for(int i = 1; i <= n; i++){
        leftb[i] = leftb[i-1];
        if(s[i-1] == 'b') leftb[i]++;;
    }
    for(int i = n-1; i >= 0; i--){
        righta[i] = righta[i+1];
        if(s[i] == 'a') righta[i]++;
    }
    int res = n; //最好的情况就是不删除
    for(int i = 0; i <= n; i++) res = fmin(res,leftb[i]+righta[i]);
    return res;
}

Leetcode1567乘积为正数的最大子数组

int getMaxLen(int* nums, int numsSize){
    int n = numsSize;
    int f[n+10]; //以nums[i]结尾乘积为正数的最长子数组长度
    int g[n+10]; //以nums[i]结尾乘积为负数的最长子数组长度
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    if(nums[0] > 0){
        f[0] = 1;
    }
    else if(nums[0] < 0) g[0] = 1;
    for(int i = 1; i < n; i++){
        if(nums[i] > 0){
            f[i] = f[i-1] + 1;
            if(g[i-1] > 0) g[i] = g[i-1] + 1;
            else g[i] = 0; 
        }
        else if(nums[i] == 0){
            f[i] = 0;
            g[i] = 0;
        }
        else{
            g[i] = f[i-1] + 1;
            if(g[i-1] > 0) f[i] = g[i-1] + 1;
            else f[i] = 0;
            
        }
    }
    for(int i = 0; i < n; i++) printf("%d ",f[i]);
    printf("\n");
    for(int i = 0; i < n; i++) printf("%d ",g[i]);
    printf("\n");
    int res = 0;
    for(int i = 0; i < n ;i++) res = fmax(res,f[i]);
    return res;
}