算法小试炼(差不多相当于重新过一遍ACWING,为了夏令营做点准备)
1.最长不重复子串
这个题目的具体意思就不用我说了,我这里给出两种算法
1)暴力搜索
只要机器够快,没有什么是暴搜解决不了的^ ^(开玩笑
很简单,我们只需要遍历长度,跟左边界就好了,这个应该没什么好说的
s = input()
n = len(s)
def solve(s): # 判断字符串是否有重复,返回True 代表没重复
charstr = set()
for ch in s:
if ch in charstr:
return False
charstr.add(ch)
return True
res = 1
for maxl in range(2,n + 1): # 字符串长度
for i in range(n - maxl + 1): # 左边界
s2 = s[i : i + maxl]
if solve(s2): res = maxl # 我们的maxl是递增的,不用比较
2)滑动窗口
我们很明显的就能看出那个暴搜其实浪费了很多资源的,例如如果从1-5的子序列已经有重复的了,就不用再搜1-6的子序列了,于是,滑动窗口的思想应运而生
我们有两个指针,left 和 right,right先动,如果遍历到的元素不在set中,就把它加进去,并且lens + 1,反之,我们让left动,left去删除他遍历到的元素,直到right指针指到的元素不在set中
具体代码如下
s = input()
n = len(s)
left, right, lens, maxlen = 0, 0, 0, 0
strset = set()
while right < n:
if s[right] not in strset:
strset.add(s[right])
right += 1
lens += 1
maxlen = max(lens,maxlen)
else:
while (s[right] in strset):
strset.remove(s[left])
left += 1
lens -= 1
print(maxlen)
2.快排
快排的思想很简单,就是举一个数,然后找到这个数该在的位置,让这个数的左边都是小于他的,右边都是大于他的,分治做下去(这个数是否要变到他应该在的位置并不重要)
具体代码
n = int(input())
a = [int(x) for x in input().split()]
def quicksort(a,l,r):
if l >= r : return
x = a[l]
i, j = l - 1, r + 1
while (i < j):
i += 1
j -= 1
while (a[i] < x):
i += 1
while (a[j] > x):
j -= 1
if (i < j): a[i], a[j] = a[j], a[i]
quicksort(a,l,j)
quicksort(a,j + 1,r)
quicksort(a,0,n - 1)
print(' '.join(map(str,a)))
3.归并排序
也是采取了分治思想,用一张图可以很好的展示分治排序

局部有序 --> 全局有序
具体代码如下
n = int(input())
a = [int(x) for x in input().split()]
def merge_sort(a,l,r):
if l >= r : return
mid = (l + r) // 2
merge_sort(a, l, mid)
merge_sort(a, mid + 1, r)
temp = []
i,j = l,mid + 1
while (i <= mid and j <= r) :
if a[i] < a[j]:
temp.append(a[i])
i += 1
else:
temp.append(a[j])
j += 1
if i <= mid:
temp += a[i : mid + 1]
else:
temp += a[j : r + 1]
a[l : r + 1] = temp[:]
merge_sort(a, 0, n - 1)
print(' '.join(map(str,a)))
4.整数二分
这个其实就两个模板,具体问题具体套一下
第一种就是 mid = (l + r) // 2,这时候要看a[mid] >=k r = mid
第二种就是 mid = (l + r + 1) // 2,这时候就看 a[mid] <=k l = mid
else的话只需要注意,r 永远是l - 1就好了
具体代码如下
## 整数二分,找到值在列表中的范围
# 第一行数n 和要查询的个数
# 第二行是单调递增的数组
# 其余后面几行是查询的数
# 浮点数二分没有那么复杂,没有+1 -1
n ,q = map(int, input().split())
a = [int(x) for x in input().split()]
for i in range(q):
l ,r = 0, n - 1
k = int(input()) # 要查询的数
# 第一种模板
while (l < r):
mid = (l + r) // 2
if (a[mid] >= k):
r = mid
else:
l = mid + 1
if a[l] != k : print('-1 1')
else:
print(l, end = ' ') # l相当于左边界
print(r)
# 第二种模板
l ,r = 0, n - 1
while (l < r):
mid = (l + r + 1) // 2
if (a[mid] <= k):
l = mid
else:
r = mid - 1
print(l) # 这个l相当于右边界
5.一维前缀和
这个没啥好说的,就是为了能快速查到数组从 l 到 r的和
# 找a[l] +…+ a[r]很方便 , 下标从1开始
n ,m = map(int,input().split())
a = [0] + [int(x) for x in input().split()]
s = [0] * (n + 1)
for i in range(1,n + 1):
s[i] = s[i - 1] + a[i]
for i in range(m): # m次查询
l, r = map(int,input().split())
print(s[r] - s[l - 1])
---------------现在反应过来不能一个个练了太慢了,我直接调到图论和DP,重点再过一下这两部分
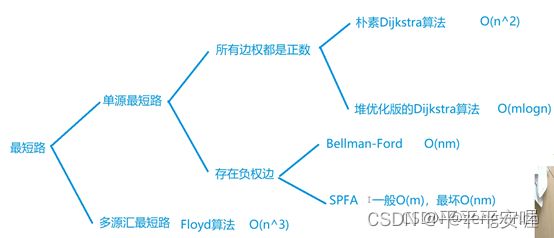
6.dijkstra
这个其实还是蛮简单的,就是要熟练,我回过头来写起来已经有点吃力了现在
dijkstra的原理很简单,就是每次重复n(点的个数)次,每次找到一个与原点距离最短的点,拿他去更新原点到其他点的距离,具体的证明我这里就不阐述了,时间复杂度是n^2,好像有一种堆优化的方法能做到复杂度为mlogn

具体代码如下
N,null = 510,0x3f3f3f3f
def dijkstra():
dist[1] = 0
for _ in range(n): # 更新n次 因为有n个点,每次确定一个
t = -1
# 找出没有被确认的最短路径的点集合中离源点最近的点
for j in range(1,n+1):
if (not st[j] and (t == -1 or dist[t] > dist[j])): # 他是第一个点 或者后面的点距离原点的距离比他小
t = j
st[t] = True
for j in range(1,n+1): # 用t去更新 其实只要更新不确定的,但为了代码方便就全部一起更新
dist[j] = min(dist[j],dist[t] + g[t][j])
if dist[n] == null : return -1
else: return dist[n]
if __name__ == '__main__':
g = [[null]*N for _ in range(N)] # 稠密图用邻接矩阵
dist,st = [null]*N,[False]*N # dist用于存储每个点到起点的距离 st用于表示当前点已经确定最短了
n,m = map(int,input().split())
for _ in range(m):
x,y,z = map(int,input().split())
g[x][y] = min(g[x][y],z) # 可能有重边 取最小的
print(dijkstra())
7.bellman-ford
这个算法就是去根据边的信息去更新多次,最终要更新n(点的个数)次,就能求出来1到n的最短路
这个算法的好处是:1.允许有负边,2.他可以限制从1到n最多能经过几条边(等等看题)
具体代码如下
N, null = 100010, 0x3f3f3f3f
import copy
def bellman_ford():
dist[1] = 0
for _ in range(k): # 遍历k次,因为有限制
last = copy.deepcopy(dist) # 复制一下,只有限制边数才用到,怕会发生串联
for j in range(m): # 遍历遍历都更新所有的边
a, b, c = edges[j]
dist[b] = min(dist[b], last[a] + c)
if dist[n] > null / 2: print('impossibile')
else: print(dist[n])
if __name__ == '__main__':
n, m, k = map(int,input().split())
dist = [null] * N
edges = []
for _ in range(m):
x, y, z = map(int,input().split())
edges.append((x, y, z))
bellman_ford()
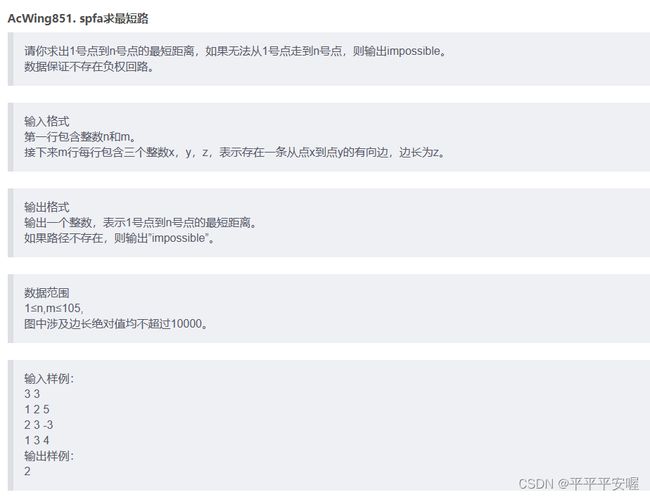
8.spfa
这个算法其实就是对bellman-ford的改进,最坏情况下跟bellman-ford算法时间复杂度一样(好像一般比赛都会卡这个),他引入了一个思想就是,只有被更新的点才能去更新其他点,具体看代码把,我不是很喜欢用链表存储,点的个数太多的话邻接矩阵要开100000*100000,显然太大了,可以考虑使用两个列表分别存储点的连接和点的权重(如果不用链表的话),应该蛮好实现的,我这里就直接用邻接矩阵了哈
具体代码如下
##我还是不喜欢用链表存,我感觉有点麻烦
from collections import deque
def spfa():
dist[1] = 0
q = deque([1])
while q:
t = q.popleft() # 弹出开头的元素
st[t] = False # 他就不在队列中了
for i in range(1, n + 1): # 这一步其实是要找到和t相连的结点,但是我没什么好的办法,只能遍历所有的
if g[t][i] == null:continue
if dist[i] > dist[t] + g[t][i]:
dist[i] = min(dist[i], dist[t] + g[t][i])
if not st[i]:
q.append(i)
st[i] = True
if dist[n] > null / 2: print('impossible')
else: print(dist[n])
N = 510
null = 0x3f3f3f3f
dist, st = [null] * N, [False] * N
g = [[null] * N for _ in range(N)]
n, m = map(int,input().split())
for _ in range(m):
x, y, z = map(int,input().split())
g[x][y] = min(g[x][y], z)
spfa()
9.spfa判断负环
他判断负环的方式其实很简单,只要有一个边,被更新了n次以上,就代表有负环了,所以只需要在原来的代码下改一点就好了,要注意的是开头我们要把所有的点都加入到队列中,因为1号点可能走不到负环
具体代码如下
##我还是不喜欢用链表存,我感觉有点麻烦
from collections import deque
def spfa():
dist[1] = 0
q = deque([x for x in range(1,n+1)]) # 是因为可能从1号点走不到负环。所以需要以所有点都走一下试试
while q:
t = q.popleft() # 弹出开头的元素
st[t] = False # 他就不在队列中了
for i in range(1, n + 1): # 这一步其实是要找到和t相连的结点,但是我没什么好的办法,只能遍历所有的
if g[t][i] == null:continue
if dist[i] > dist[t] + g[t][i]:
dist[i] = min(dist[i], dist[t] + g[t][i])
cnt[i] = cnt[t] + 1
if cnt[i] >= n : return 'Yes'
if not st[i]:
q.append(i)
st[i] = True
return 'No'
if __name__ == '__main__':
N = 510
null = 0x3f3f3f3f
dist, st = [null] * N, [False] * N
cnt = [0] * N
g = [[null] * N for _ in range(N)]
n, m = map(int,input().split())
for _ in range(m):
x, y, z = map(int,input().split())
g[x][y] = min(g[x][y], z)
spfa()
10.flord
这种n^3的做法就蛮暴力的感觉哈哈,这个没什么好说的,三个for就完事儿了

具体代码如下
N, null= 210, 0x3f3f3f3f
def flord():
for k in range(n + 1):
for i in range(n + 1):
for j in range(n + 1):
g[i][j] = min(g[i][j], g[i][k] + g[k][j])
if __name__ == '__main__':
n, m, k = map(int,input().split()) # k次查询
g = [[null] * N for _ in range(N)]
for i in range(n + 1): # flord是在g上更新,所以要做这一步
g[i][i] = 0
for _ in range(m):
x, y, z = map(int,input().split())
g[x][y] = min(g[x][y], z)
flord()
for _ in range(k):
x, y = map(int, input().split())
if g[x][y] > null / 2: print('impossible')
else: print(g[x][y])