ACWING蓝桥杯每日一题python

ACWing蓝桥杯每日一题

一直没时间去总结算法，终于有空可以总结一下刷的acwing了，因为没时间所以最近只刷了ACWING的蓝桥杯每日一题。。。真是该死

1.截断数组

首先我们要知道，如果sum(a)不能被3整除或者len(a) < 3 ，那么他肯定没法让截断的三个子数组和都一样
然后我们只要把平均值算出来，从前往后遍历，我们会得到1average截断点，也会得到2average截断点，意思就是说在1average截断点前的子数组加和为average ，那么其实答案就是 2average截断点的个数 + 在2average截断点之前的 1average截断点的个数，，所以我们只要让当tot = 2average时，答案 += 当时的1average 截断点的个数就好了

注意！在判断tot = average 还是 2average 时，要先判断是否等于2average，因为当tot等于0时，1average == 2average，你如果先判断了2*average，就会把1级截断点和二级截断点在同一个地方。。

同时考虑到数组全为0的情况，那么这种情况我们就C（len-1,2）就行了

具体代码如下

n = int(input())
a = [int(x) for x in input().split()]
def c(a,b):
    res = 1
    while b:
        res = res * a / b
        a -= 1
        b -= 1
    return int(res)
if sum(a) % 3 != 0 or len(a) < 3:
    print(0)
elif a == [0]*len(a):
    print(c(len(a)-1,2))
else:
    average = sum(a) // 3
    one = 0
    res = 0
    tot = 0
    for i in range(n-1): # 最后一个点不能考虑进去，要留下一个做第三部分
        tot += a[i]
        
        if tot == 2*average: res += one
        if tot == average:one += 1
        
    print(res)

2.改变数组元素

初始化一个V 数组，大小为（n+1）初始化都是0
只需要去通过i去遍历a[i],遍历到第i次时，我们就把 i - a[i] + 1 到 i 全部加1，
i就可以代表V数组实际的长度应该是多少，例如当i = 5 ，那么其实V数组实际上长度是5，因为末尾只被加了5个0 ，然后假设a[5] = 2 ，那就是V[4] 和 V[5] + 1 ，这里为什么可以+ 1 不用让他等于1？因为整个流程没有减过，所以只要这个位置不等于0，就代表他被改变过，一定等于1
然后这种从i - a[i] + 1 到 i 全部加1的实现通过差分就很好实现了

具体代码如下

def add(l,r):  # 差分,最后前缀和后L到R + 1
    V[l] += 1
    V[r+1] -= 1 

t = int(input())
for _ in range(t):

    ## 第i次就等于从i- a[i] + 1到i 全变为1
    ## 利用差分，从 i - a[i] + 1 到 i 全部加1 ，因为不会减，所以最后只要前缀和不是0就代表他被换过
    n = int(input())
    a = [int(x) for x in input().split()]
    V = [0]*(n+1) #直接开一个这么大的数组,直接开N  TLE了
    for i in range(1,n+1):  # i要从1开始，i等于1表示数组中末尾添加了一个0
        if a[i-1] == 0:continue
        if (a[i-1] >= i):
            add(0,i-1)
        else:
            add(i - a[i-1],i-1)
    for i in range(n):
        V[i+1] += V[i]
    for i in range(n):
        if V[i] != 0 :print(1,end = ' ')
        else: print(0,end = ' ')
    print()

3.我在哪？

这题我觉得主要的就是需要考虑到字符串的哈希存储，因为字符串没法像数组那样去用下标来找到第几个字母，所以得先将字符串进行哈希存储，然后再遍历遍历列表，例如k = 4 ，就字符串前四个的值放入集合中，然后字符串2-5的哈希值看看在不在集合中，如果在，就返回False
然后要找K的话其实从1开始遍历就好了，只不过那样时间复杂度是O（n）很可能会被卡，最好用二分

具体代码如下

字符串哈希

## 核心思想：将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
##  小技巧：取模的数用2^64，溢出的结果就是取模的结果
## h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
N = 10**5 +10
P = 131
M = 91815541
h = [0] * N
p = [0] * N
p[0] = 1
n = int(input())
s = " " + input()
for i in range(1,n+1):
    h[i] = h[i-1]*P + ord(s[i]) % M
def get(l,r):
    return (h[r] - h[l-1] * P**(r-l+1)) % M
def check(k):
    a = set()
    for i in range(1,n - k + 2):
        if get(i,i + k -1) in a:
            return False
        else:
            a.add(get(i,i+k-1))
    return True

if __name__ == '__main__':
    l,r = 1,n
    while l < r:
        mid = (l + r) >> 1
        if check(mid): r = mid
        else: l = mid + 1
    print(r)

4.字符串删减

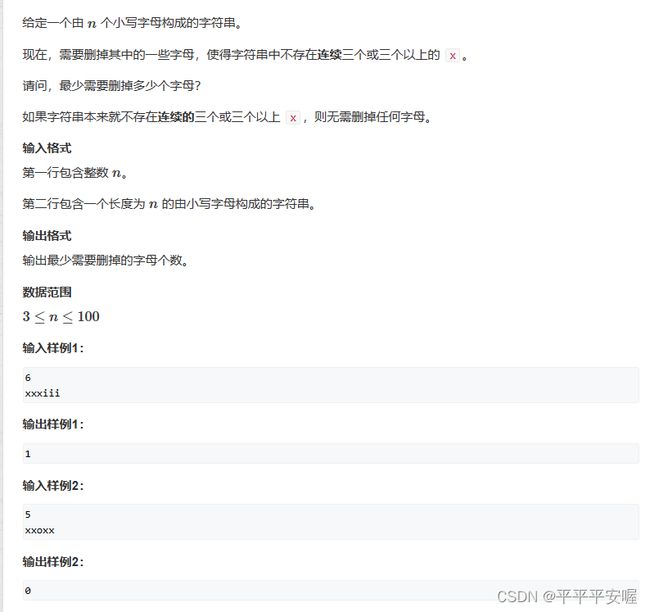
这个相对于Python来说就很好做吧，别的我不知道，就是记录一下连续x的长度，然后最后计算一下就好了，直接看代码吧

具体代码如下

n = int(input())
s = input()
lens = 0
lenshuzu = [] # 记录每一段连续的数组
for i in s:
    if i == 'x':
        lens += 1
    else:
        lenshuzu.append(lens)
        lens = 0
lenshuzu.append(lens)
res = 0
for i in lenshuzu:
    if i >= 3:
        res += i - 2
print(res)

5.砖块

这题我选择算是用贪心的方法去做吧，分为两种，全变黑和全变白
如果是全变白，那么就当看到黑的砖块，就把他变白就好了
后面的输入操作的我可能是写的有点麻烦了。。有大佬有更简便的可以指导一下

具体代码如下

T = int(input())
for _ in range(T):
    k = int(input())
    p = input()
    p2 = p #记录一下
    p = list(p)
    caozuo1 = []
    ans1 = 0
    flag1 = False
    flag2 = False
    # 全变白色
    for i in range(k-1):
        if p[i] == 'B':
            p[i] = 'W'
            if p[i+1] == 'B':p[i+1] = 'W'
            else: p[i+1] = 'B'
            caozuo1.append(i+1)
            ans1 += 1
    if p == ['W']*k :flag1 = True
    
    # 全变黑色
    p2 = list(p2)
    caozuo2 = []
    ans2 = 0
    for i in range(k-1):
        if p2[i] == 'W':
            p2[i] = 'B'
            if p2[i+1] == 'W':p2[i+1] = 'B'
            else: p2[i+1] = 'W'
            caozuo2.append(i+1)
            ans2 += 1
    if p2 == ['B']*k:flag2 = True
    if flag1 and flag2:
        if ans1 < ans2:
            print(ans1)
            if caozuo1:
                for i in caozuo1:
                    print(i,end = ' ')
                print()
            continue
        else:
            print(ans2)
            if caozuo2:
                for i in caozuo2:
                    print(i,end = ' ')
                print()
            continue
    if flag1:
        print(ans1)
        if caozuo1:
            for i in caozuo1:
                print(i,end = ' ')
            print()
        continue
    if flag2:
        print(ans2)
        if caozuo2:
            for i in caozuo2:
                print(i,end = ' ')
            print()
        continue
    print(-1)

6.树的遍历

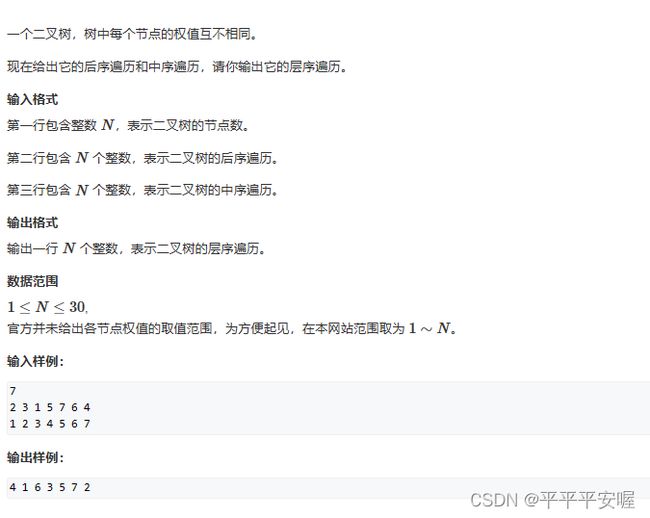
这题就递归做，可以通过中序和后序找到根节点的左右子树的中序和后序，然后递归往下建立

建立完一棵树之后就用Dfs去搜索就好了

具体代码如下

class TreeNode(object):
    def __init__(self,x):
        self.val = x
        self.left = None
        self.right = None

class Solution(object):
    def buildTree(self,inorder,postorder):  # inorder是中序，postorder是后序
        if not postorder:
            return None
        root = TreeNode(postorder[-1])
        root_index = inorder.index(postorder[-1]) # 根节点在中序中的坐标
        left_i = inorder[:root_index] # 根据中序确定左右子树
        right_i = inorder[root_index + 1:]
        len_li = len(left_i)  # 左子树长度
        left_p = postorder[:len_li]  # 确定后序遍历的左右子树
        right_p = postorder[len_li:-1]

        root.left = self.buildTree(left_i,left_p)
        root.right = self.buildTree(right_i,right_p)
        return root
def bfs(root):  #广搜进行层序遍历
    if root == None:
        return
    q = []
    q.append(root)
    head = 0
    while len(q)!=0:
        print(q[head].val,end=' ')

        if q[head].left != None:
            q.append(q[head].left)

        if q[head].right != None:
            q.append(q[head].right)

        q.pop(0)


n = int(input())
    
posto = [int(x) for x in input().split()]
inord = [int(x) for x in input().split()]
    
solution = Solution()
root = solution.buildTree(inord,posto)
bfs(root)

7.亲戚

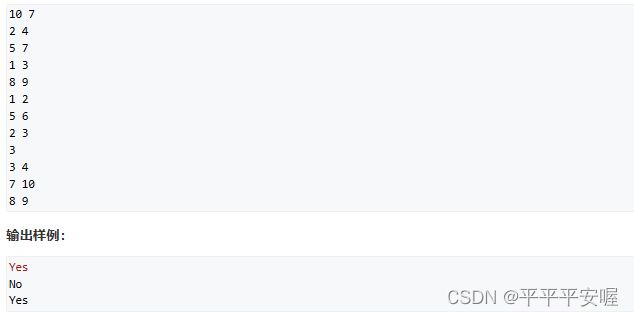
啊这题典型的并查集，让同样是亲戚的有同一个祖先就好了，不用管祖先是谁
简单说一下并查集吧
就是有一个p数组，代表自己的父亲是谁，然后就是每次遍历两个a,b，如果a和b没有同一个祖先，我们就让a的祖先 去 变成b的祖先的儿子，这样a和b就有同一个祖先了吧？
然后怎么找a和b的祖先呢，这也是并查集的精髓所在，一个find函数

def find(x):
    if p[x] != x:
        p[x] = find(p[x])
    return p[x]

如果x的父亲不是自己，就代表x不是这个家族的祖先对吧，那么让p[x]等于find(p[x])，find(p[x])就是找到p[x]的祖先，一层一层网上找，这个find函数的精髓在于，他会让p[x] = find(p[x]) 就是如果你现在他这个找到祖先的一条线的P[x]都会直接变为他们的祖先，而不是他们的父亲
然后就很好做了，看看他们的祖先是否一样就能代表是不是一个群体了

具体完整代码如下

import sys
# 不知道为什么用map(int,input().split())会被卡。。
N, M = map(int, sys.stdin.readline().strip().split())
p = [i for i in range(N + 1)]

def find(x):
    if p[x] != x:
        p[x] = find(p[x])
    return p[x]

for i in range(M):
    a, b = map(int, sys.stdin.readline().strip().split())
    pa, pb = find(a), find(b)
    if pa != pb:
        p[pa] = pb
q = int(input())
for i in range(q):
    a, b = map(int, sys.stdin.readline().strip().split())
    if find(a) == find(b):
        print('Yes')
    else:
        print('No')

8.笨拙的手指

这题我的想法是，把二进制的每一位都变一下，就是把可能的正确答案都存在一个列表中，然后去对比二进制和三进制的列表，找到相同的，二进制的好做，0和1之间变换只要用^就可以了，三进制就需要在遍历一下1-3 ，如果与当前位不同再去变，看代码吧，蛮容易看懂的，比我写清晰多了

具体代码如下

import copy
er = input()
three = input()
erjinzhi = []
sanjinzhi = []
for i in range(len(er)):
    erjinzhi.append(int(er[i]))
for j in range(len(three)):
    sanjinzhi.append(int(three[j]))
res_2 = []
res_3 = []
copy_erjinzhi = copy.deepcopy(erjinzhi)
for i in range(len(erjinzhi)):  #勉强算20
    erjinzhi = copy.deepcopy(copy_erjinzhi)
    erjinzhi[i] = erjinzhi[i] ^ 1
    lenlen = 2**(len(erjinzhi)-1)
    res = 0
    for j in erjinzhi:
        res += j*lenlen
        lenlen >>= 1
    res_2.append(res)
    
    

copy_sanjinzhi = copy.deepcopy(sanjinzhi)
for i in range(len(sanjinzhi)):  #勉强算20

    for j in range(3):
        sanjinzhi = copy.deepcopy(copy_sanjinzhi)
        if sanjinzhi[i] != j:
            sanjinzhi[i] = j
            lenlen = 3**(len(sanjinzhi) - 1)
            res = 0
            for k in sanjinzhi:
                res += k*lenlen
                lenlen //= 3
            res_3.append(res)
res = 0
for i in res_2:
    for j in res_3:
        if i == j:
            res = max(res,i)
print(res)

9.裁剪序列

我也没搞懂。。抱歉

10.周期

首先，我们要知道KMP算法的next数组是什么用的，他是可以找到后缀和前缀相同的个数的一个数组，具体求法可以看我的KMP手写算法那一个

然后我们只需要从头到尾扫一遍，只要（i % (i-next[i])）== 0 就代表有重复节，并且长度是i // ( i - next[i])
例如 abcabcabcabc 当i等于12时，就是全长了嘛，然后next[i] = 9
满足条件吧？ 长度为4

具体代码如下

def find_next(p):
    next = [0] * (len(p)+1)
    j,k = 0,-1
    next[0] = -1  # 防止死循环 k一直等于0 j也不加
    while(j <= len(p) - 1):
        if (k == -1 or p[j] == p[k]):
            j += 1
            k += 1
            next[j] = k
        else:
            k = next[k]
    next[0] = 0
    return next

if __name__ == '__main__':
    flag = 1
    while True:
        n = int(input())
        if n == 0: break
        print('Test case #{}'.format(flag))
        s = input()
        next = find_next(s)
        for i in range(2,n+1):
            if i % (i - next[i]) == 0 and next[i]:
                print('{} {}'.format(i,i//(i - next[i])))
        print()
        flag += 1

11.最大异或和

先求出前i个数的异或和sum[i]，再在大小为m的滑动窗口内进行trie.

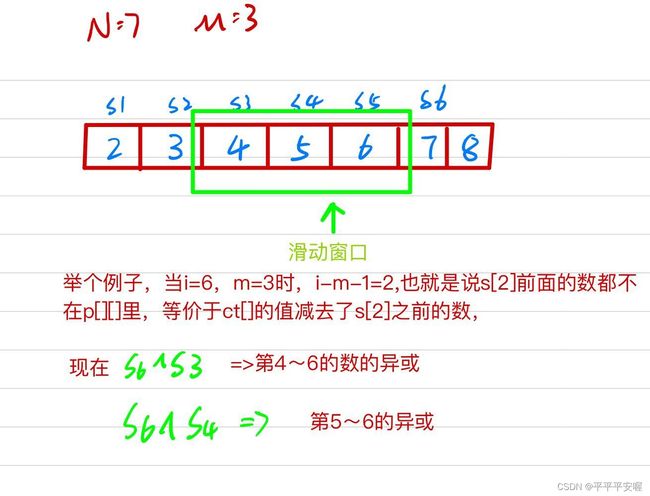
参考自https://www.acwing.com/solution/content/48648/
用trie树嘛，每个数都被记录在一个trie树中，一个二分数，每个节点都有一个0，1孩子，我们这边用了30层，完全够用了，然后把每个数的二进制数给存进去
先计算前缀异或和s[i]
要求异或和a[l]^…a[r] 转化为前缀异或和数组(s[r]^s[l-1])

具体代码如下

N = 100010 * 31
M = 100010
son = [[0]*2 for _ in range(N)]  #　son[p][n] n 只有两个取值为0和1，
idx = 0
s = [0]*M
cnt = [0]*N # cnt变量表示这个节点在构建字典树的时候保存了几次
# 遍历的时候，如果节点的cnt>0，就代表可以接着往下走，
def insert(x,v):
    
    global idx,son,s,cnt
    p = 0
    for i in range(30,-1,-1):
        # 意思就是一棵树有30层，来代表每个数的二进制数
        u = x >> i & 1
        if(int(not son[p][u])):  # p的儿子有0和1两条路径
            idx += 1
            son[p][u] = idx
        p = son[p][u]            #p变为儿子，如果v是1，那么这条路径的p的1儿子+1
        cnt[p] += v              
        

### 我们遍历的话肯定是想从最高位开始，走1的分支，因为那样异或和才会更大
def query(x):
    # res 初始值为s[i]
    res = x
    p = 0
    for i in range(30,-1,-1):
        u = x >> i & 1       # x的二进制的第i位
## 现在x的第i位是u ，所以我们要走跟u相反的，这样他们异或才会为1
        if cnt[son[p][int(not u)]]:  # 就是存在和不存在 p 有两个儿子嘛，一个是0一个是1，如果u是1，就要看p的0的儿子还有没有
            u = int(not u)

        res ^= u << i  # u << i 因为之前 u = x >> i & 1 了，现在还回去
        # print(res)
        p = son[p][u]  # 接着往下走
    return res


if __name__ == '__main__':
    n,m = map(int,input().split())
    a = [int(x) for x in input().split()]
    for i in range(1,n+1):
        s[i] = s[i-1]^a[i-1]

    insert(s[0],1)
    Res = 0
    for i in range(1,n+1):
        if i > m :
            insert(s[i - m - 1],-1)

        Res = max(Res,query(s[i]))
        insert(s[i],1)        # 把s[i]加入到树中
    print(Res) 

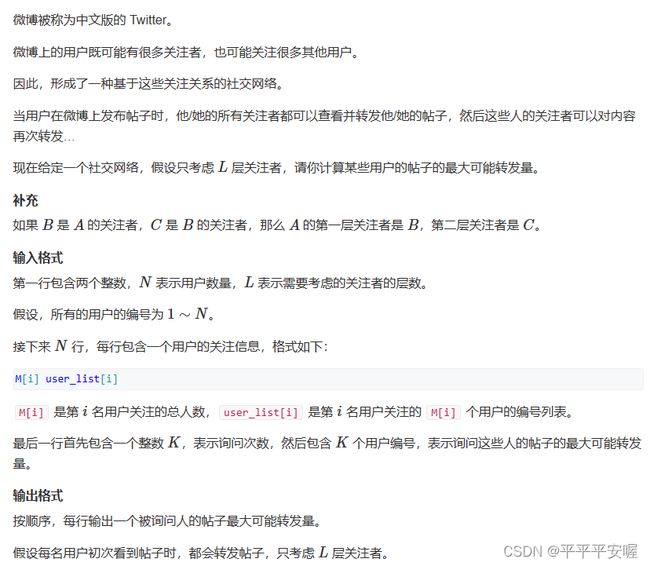
12.微博转发

一个很传统的bfs模板，只需要记录每个人的粉丝，然后去遍历L层就好了

具体代码如下

N = 1010
son = [[] for _ in range(N)]
from collections import deque
st = [False] * N
N,L = map(int,input().split())
for i in range(1,N+1):
    M = [int(x) for x in input().split()] # 记录一下第i个的信息
    if M[0] != 0:  # 如果用户i有关注人的话
        for j in range(M[0]):
            son[M[j+1]].append(i)      # son记录的是谁关注了你
K = [int(x) for x in input().split()]
def bfs():  #传统bfs
    res = -1
    for _ in range(L+1):  # 遍历L次
        sizes = len(q)
        for _ in range(sizes): # 每次只遍历他这一层的数
            tmp = q.popleft()
            if not st[tmp]:    # 这个人没被传播过
                res += 1
                for i in son[tmp]:
                    q.append(i)
                st[tmp] = True
    return res
for i in range(K[0]):
    st = [False] * 1010
    k = K[i+1]
    q = deque()
    q.append(k)
    print(bfs())

13.不同路径数

这是一个很标准的深搜题，感觉不需要讲太多，看看代码就很好看懂了

具体代码如下

n,m,k = map(int,input().split())
migong = [] 
res = 0
s = [False] * 1000010  # 最多六位数
for _ in range(n):
    migong.append([int(x) for x in input().split()])  # 存储迷宫
directions = [(1,0),(-1,0),(0,1),(0,-1)]   # 四个方向
def dfs(i,j,p,o):
    global res
    if p == k:     # P是长度，长度为k的时候，组成的数字要是之前没有过，res就+1
        if not s[o]:
            s[o] = True
            res += 1
        return 
    for direction in directions:
        x,y = i + direction[0],j+direction[1]
        if x >= 0 and x < n and y >= 0 and y < m:    # 四个方向都走一遍
            dfs(x,y,p+1,10*o + migong[x][y])         # 深搜

for i in range(n):
    for j in range(m):
        dfs(i,j,0,migong[i][j])  # 每个点为起点都深搜一下
print(res)

14.构造有向无环图

首先我们要判断他原来是否是个有环图，如果是的话肯定就Pass了，就看拓扑排序的总数量是否是n就好了，如果是个有环图，拓扑排序出来的结果数不可能是n，因为环不会加入到拓扑排序中
然后只要跟着拓扑排序的顺序，去添加无向边的方向，就一定不会构成有环图拉

具体代码如下

import collections 
T = int(input())
def topsort():        # 拓扑排序并判断是否会构成有环图
    Q = collections.deque()
    for x in range(1,n+1):
        if indegree[x] == 0:
            Q.append(x)
    cnt = 0
    while Q:
        x = Q.popleft()
        rec_topsort.append(x)
        cnt += 1
        for y in adjvex[x]:
            indegree[y] -= 1
            if indegree[y] == 0:Q.append(y)
    return cnt == n



for _ in range(T):
    n,m = map(int,input().split())
    adjvex = collections.defaultdict(list)  # 有向边
    indegree = [0 for _ in range(n+1)] # 入度
    aedge = []  # 无向边
    
    for _ in range(m):
        t,x,y = map(int,input().split())
        if t == 1:
            adjvex[x].append(y)  # X --> Y
            indegree[y] += 1
        else:
            aedge.append((x,y))
    
    rec_topsort = []  # 拓扑排序
    
    if not topsort():print('NO')
    else:
        print('YES')
        x_pos = dict()
        for i, x in enumerate(rec_topsort):
            x_pos[x] = i
        
        for x,y in aedge:           #通过拓扑排序去构建无向边的方向，这样无论如何都不会构成有向图
            if x_pos[y] < x_pos[x]:
                x,y = y,x
            print("{} {}".format(x,y))
        for x,ys in adjvex.items():
            for y in ys:
                print("{} {}".format(x,y))

15.最短距离

dijkstra算法咯，把距离存在一个矩阵里，然后就是标准的dijkstra算法，感觉这个题都挺好的，都蛮有代表性，记得要把模板记住就很好做

具体代码如下

from collections import deque
N,M = map(int,input().split())
max_c = 10010
g = [[max_c]*(N+1) for _ in range(N+1)]
for _ in range(M):
    a,b,c = map(int,input().split())
    g[a][b] = c 
    g[b][a] = c
K = int(input())
store = []
for _ in range(K):
    x = int(input())
    store.append(x)
Q = int(input())
for _ in range(Q):
    dist = [max_c]*(N+1)
    st = [False] * (N+1)
    y = int(input())
    dist[y] = 0
    for _ in range(N+1):
        t = -1
        for j in range(1,N+1):
            if (not st[j] and (t == -1 or dist[t] > dist[j])): 
                t = j
        st[t] = True       # 找到一个距离选中集合最近的点
        for j in range(N+1):
            dist[j] = min(dist[j],dist[t] + g[t][j],dist[t] + g[j][t])  # 加入了之后更新所有的距离

    res = max_c
    for i in store:
        res = min(dist[i],res)
    print(res)

16.作物杂交

这题我在蓝桥杯做过，用的是深搜，但是在这里深搜过不了，由于我是备战蓝桥杯，所以这里就用深搜了，但是这题应该是spfa的题
深搜的话就很简单了，从想要的种子，开始往下搜索，比如我想要6号种子，我就去看谁和谁杂交会得到他？假设种子1+种子2杂交会得到他，那么得到种子6的时间就会等于 max(得到1的时间，得到2的时间) + max(各自成熟的时间)）这样一层层递归下去

具体代码如下

# 蓝桥杯能过代码，这里会报Runtime error

N,M,K,T = map(int,input().split())
time = [int(x) for x in input().split()]  # 第i种作物种植时间
have = [int(x) for x in input().split()]  # 已有的种子
cross = [[] for _ in range(N+1)]
for _ in range(K):
    a,b,c = map(int,input().split())
    cross[c].append((a,b))
st = [False]*(N+1) # 是否确定最短路
g = [100000]*(N+1) #　最短路
for i in have:
    st[i] = True
    g[i] = 0
def dfs(u):
    if st[u] : return g[u]
    for a,b in cross[u]:
        g[u] = min(g[u],max(dfs(a),dfs(b)) + max(time[a-1] , time[b-1]))
    st[u] = True
    return g[u]
print(dfs(T))

17.铁路和公路

这题是不用考虑在中途火车和汽车会撞到一起的，因为如果说到i这个城市，火车可以到i，那么就代表汽车不能直接到i，所以说，我们只需要求到达目的地的两个车的最短时间，取个最大值
由于数据量都比较小，就用floyd
首先就是铁路和公路的建立，这个应该好建，然后floyd也好写把，就三层循坏，o(n^3)时间复杂度，但这题数据小噢所以就直接用这个了也好写

具体代码如下

n,m = map(int,input().split())
inf = 1000
road = [[False]*(n+1) for _ in range(n+1)]
a = [[inf] * (n+1) for _ in range(n+1)]  # 铁路
b = [[inf] * (n+1) for _ in range(n+1)]  # 公路
for i in range(n+1):
    a[i][i] = 0
for _ in range(m):
    x,y = map(int,input().split())
    road[x][y] = road[x][y] = True
    a[x][y] = a[y][x] = min(a[x][y],1)  #  有铁路距离就为1了
for i in range(1,n+1):
    for j in range(1,n+1):
        if not road[i][j] and not road[j][i]:
            b[i][j] = min(b[i][j],1)
def floyd():
    for k in range(1,n+1):
        for i in range(1,n+1):
            for j in range(1,n+1):
                a[i][j] = min(a[i][j],a[i][k] + a[k][j])
    if a[1][n] == 1000:
        return -1
    
    for k in range(1,n+1):
        for i in range(1,n+1):
            for j in range(1,n+1):
                b[i][j] = min(b[i][j],b[i][k] + b[k][j])
    if b[1][n] == 1000:
        return -1
    return max(a[1][n],b[1][n])

print(floyd())

18.城市通电

这种通电的感觉就是最小生成树，之前是大概搞懂了，但今天太累了不想再去理一遍，以后再回头来捋把

具体代码如下

INF = 10 ** 16

n = int(input())
nodes = []
for _ in range(n):
    x, y = map(int, input().split())
    nodes.append((x, y))

cs = [] + [int(x) for x in input().split()]
ks = [] + [int(x) for x in input().split()]

edge = [[INF for _ in range(n + 1)] for _ in range(n + 1)]
for i in range(n):
    for j in range(i, n):
        xi, yi = nodes[i]
        xj, yj = nodes[j]
        dist = abs(xi - xj) + abs(yi - yj)
        cost = dist * (ks[i] + ks[j])
        edge[i][j] = cost
        edge[j][i] = cost


#-------------- prim 算法求最小生成树MST 稠密图：for循环    稀疏图：才用minHeap-------------#
MST_cost = 0
MST = [False for _ in range(n + 1)]

#----初试化时，每个结点直接连发电站
dist = [INF for _ in range(n + 1)]     #从发电站 n出发
for x in range(n):
    dist[x] = cs[x]     #初始化，每个点自己连接发电站
dist_prev = [n for _ in range(n + 1)]                  #MST中点的前驱结点（与dist的初始化一致，前驱结点是发电站）

rec = []        #记录直接连接发电站的点
line = []       #记录发电线

dist[n] = 0
MST[n] = True
for _ in range(n):
    #----寻找候选区中，dist最小的点（距离MST最近的点）
    t = -1
    for x in range(n):     
        if MST[x] == False and (t == -1 or (0 <= t and dist[x] < dist[t])):
            t = x

    #----正式加入MST        
    MST[t] = True       
    MST_cost += dist[t]

    #---- 记录本题的需要
    if dist_prev[t] == n:       #从发电站连过来的
        rec.append(t)
    else:                       #不是从发电站连过来的
        line.append((dist_prev[t], t))

    #----把t加入后，产生了影响。经过t的，与MST的距离dist可能会变短
    for y in range(n):
        if MST[y] == False and edge[t][y] < dist[y]:
            dist[y] = edge[t][y]
            dist_prev[y] = t

res2 = len(rec)     #电站数量

print(MST_cost)                         #MST的花费
print(res2)                             #与发电站直接相连的点
for i in rec:       
    print(i + 1, end = ' ')             #与发电站直接相连的点们
print()
print(n - res2)                         #不用直接发电，拉电线的数量

for a, b in line:
    print("{} {}".format(a + 1, b + 1)) #拉电线的点对们

19.二叉树

用公共祖先做，这个我也是第一次接触到，就是找到两个结点的公共祖先，那么这两个的路径就会等于deep(a) + deep(b) - 2*deep(ancestor)，这个应该是好理解的把
那么怎么找共同的第一个祖先呢，看他们的深度，谁深，谁就往上走，直到他们两个一样深之后
再一起往上走，直到他们两个一样，很好理解把这逻辑
找到点的深度也很好找了，就一个递归就完事儿了，深搜嘛

具体代码如下

T = int(input())
N = 1010

import sys
sys.setrecursionlimit(10000)  # 增加递归深度，要不会出问题
def dfs(root,deep):  # 作用是找到每个点的当前深度
    if root == -1: return
    deeps[root] = deep
    dfs(l[root],deep + 1)
    dfs(r[root],deep + 1)

def LCA(x,y):  # 找到x,y最近的公共祖先
    while deeps[x] > deeps[y]:  # x深x就往上走
        x = p[x]       
    while deeps[y] > deeps[x]:
        y = p[y]
    while x != y :  # 这时候x,y应该在同一高度了，一起往上走
        x = p[x]
        y = p[y]
    return x     # 直到找到第一个相同的点
for _ in range(T):
    l,r,p,deeps = [-1]*N,[-1]*N,[-1]*N,[0]*N
    n,m = map(int,input().split())
    for i in range(1,n+1):
        left,right = map(int,input().split())
        l[i] = left
        if left != -1: p[left] = i
        r[i] = right
        if right != -1: p[right] = i
    dfs(1,1) # 初始深度为1,反正是相对的，因为我们初始为0，这里就设置为1了
    for i in range(m):
        a,b = map(int,input().split())
        print(deeps[a] + deeps[b] - 2*deeps[LCA(a,b)])

20.完美牛棚

这个就是一个很经典的匹配问题了，跟之前我了解的男女匹配问题不同，这个只有奶牛一个单方面的匹配要求
我们定义一个find函数，如果find 返回True 表示可以住下这房间，如果为False，表示无法住下这房间

先把全部代码写下，之后再一一解释

 def find(u):
    for i in range(max_numer[u]):  # 遍历u牛喜欢的房间
        v = love[u][i]  # 牛住下这个单间
        if not vis[v]:   # 如果v在这次没有被遍历过
            vis[v] = True
            if choose[v] == 0 or find(choose[v]):
                choose[v] = u
                return True
    return False
    if __name__ == '__main__':
	    N,M = map(int,input().split())  # 牛的数量以及单间的数量
	    love = [[] for _ in range(N+1)]  # 
	    choose = [0] * (N+1)  # 单间里住下了哪头牛
	
	    max_numer = [0] * (N+1)
	    for i in range(1,N+1):
	        l = [int(x) for x in input().split()]
	        max_numer[i] = l[0] 
	        for j in range(l[0]):
	            love[i].append(l[j+1])
	    res = 0
	    for i in range(1,N+1):
	        vis = [False] * (N + 1)  # 是否被访问过,每次都要重置一下，因为上次访问过的跟这次的没关系
	        if find(i) : res += 1
	    print(res)

love[u][i] 就是表示第u头牛愿意住下第i个房间
核心就是find 函数，当判断一头牛能不能住下这间房时，如果这头牛喜欢的房间已经被遍历过了，就代表这头牛不能住下这间房了，因为之前如果被遍历过就代表是不行的，如果行的话会返回True，注意：我们这个find是对一头牛来说的，我们会遍历1到N，每头牛都会find一次，如果这个位置之前没有被遍历过，并且这个地方没有人住（choose[v] == 0） 或者 住在这里的这头牛可以住下其他位置（find(choose[v])） 那么这头牛就可以住下
来解释一下为什么 find(choose[v]) 是表示原本住在这里的牛可以住到其他位置
首先choose[v] 代表的是原本住在v位置上的牛记为j吧，现在我们要考虑的问题就是find(j)的时候，j会不会选择住在v这个位置上？答案是不会的，因为我们可以看到，在这个find迭代里，vis[v]已经被打上True标签了，所以他不会再选择v这个地方去住下。

21.质数问题

思路就是，找到从2到n的质数，并记录下来，然后每记录一个质数，就要去看看他能不能由他前面的质数加和 再 + 1来表示

具体代码如下

import math
T = int(input())
for _ in range(T):
    zhisu = []
    res = 0
    n,k = map(int,input().split()) 
    for i in range(2,n+1):  #判断ｉ是否是质数
        Flag = False
        for j in range(2,int(math.sqrt(i)) + 1):
            if i % j == 0:
                Flag = True
                break
        else: zhisu.append(i)

        if Flag: continue

        if len(zhisu) >= 3:
            for l in range(len(zhisu) - 2):
                if zhisu[l] + zhisu[l+1] + 1 == zhisu[len(zhisu)-1]:
                    res += 1
                    break
    if res >= k : print('YES')
    else: print('NO')

22.消灭老鼠

统计老鼠跟机关枪有多少个斜率就好了，很简单，看代码就行

具体代码如下

n,x0,y0 = map(int,input().split())
mice = []
for _ in range(n):
    x,y = map(int,input().split())
    mice.append((x,y))
## 统计有多少个斜率就行
res = set()
for x,y in mice:  
    if x - x0 != 0:
        k = (y - y0)/(x - x0)  # 斜率
    else:
        k = 9999 
    res.add(k)
print(len(res))

23.幂次方

最基本的快速幂
X的N次方，可以不用乘以X个N ，把N用2进制数表示，这样时间复杂度就会降到logN,然后被一步都mod 233333一下就行

具体代码如下

m = 233333
x,n = map(int,input().split())
res = 1
while n:
    if n & 1:  # n的二进制第一位
        res = res * x % m
    x = x * x % m
    n = n >> 1
print(res)

如果n在他的这一位上是1，那么 res = res * x % m
然后记得x*x%m ,想一下这个逻辑
n的第一位为1就相当于 res * x
n的第二位为1那么就相当于 res * x * x
n的第三位为1 就相当于 res * x * x * x * x

24.吃水果

把小朋友分为k+1组，每个组内小朋友拿的水果都一样，但相邻的两个组的水果需要不一样
选 k + 1 组，就是从 n-1个空隙中，选择k个空隙 为C（n-1,k）
然后除了第一组有m种选法，剩下的(n-1)组都只有(m-1)组选法
因此最后应该是 C(n-1.k)m(m-1)^(n-1)
得出这个结论后，看到结果要mod998244353 ,那么我们就不能简单的去算了
要用到逆元（费马小定理）和快速幂

具体代码如下

M = 998244353
 
def qmi(a,b): # a的b次方mod m 
    res = 1
    while(b):
        if (b & 1): res = res * a % M
        b = b >> 1
        a = a * a % M
    return int(res % M)
def C(a,b):
    res = 1
    for i in range(b):
        res = res * (a-i) % M
        res = res * pow(i+1, M-2, M) % M  # 使用费马小定理求逆元
    return res

n,m,k = map(int,input().split())

print(int(C(n-1,k) * m * qmi(m-1,k) % M))

PS：逆元的作用：
在数论中，a的倒数不是1/a (100/50)%20 = 2 ≠ (100%20) / (50%20) %20 = 0

25.取石子游戏

参考自： https://www.acwing.com/solution/content/72694/

具体代码如下

T = int(input())
for _ in range(T):
    n,k = map(int,input().split())
    if k % 3 :
        if (n%3): print("Alice") # 后手必胜
        else:print('Bob')
    else:
        n %= k+1
        if n == k : # n == k  先手必胜
            print('Alice')
        else: # 否则判断n % 3 是否等于0
            if n % 3 == 0: # 后手必胜
                print('Bob')
            else:
                print('Alice')
## 参考https://www.acwing.com/solution/content/72694/

26.整数拆分

背包问题，相当于有无限个体积为1，2，4，8的物品
dp[j]表示背包容量为j的可以装下多少种
若当前物品体积为i ，那么dp[j] = (dp[j] + dp[j-i])mod10^9

具体代码如下

##相当于无限个体积为1，2，4，8的物品
MOD = 10**9
n = int(input())
dp = [0]*(n+1)
dp[0] = 1
i = 1
while i <= n:  # 选体积为i这个物品
    for j in range(i,n+1): # 背包大于i的都能选她
        dp[j] = (dp[j] + dp[j - i]) % MOD 
    i <<= 1  # 扩大两倍
print(dp[n])

27.最大的和

对于这题要求两个不重复子数组的和，我们记f[i] 表示从1-i的最大连续子数组的和，g[i]表示i-n最大连续子数组的和
用s来表示以a[i]结尾的最大连续子数组和
那么 f[i] = max(f[i-1],s)
对g[i]同理
然后遍历一下，求max就好了，具体代码如下

具体代码如下

T = int(input())
N = 50050
inf = -0x3f3f3f3f3f
for _ in range(T):
    n = int(input())
    a = [0] + [int(x) for x in input().split()]
    ## f[i] 表示 1 - i 最大连续子数组的和
    ## g[i] 表示 i 到 n 最大连续子数组的和
    f, g = [inf] * (N), [inf] * (N)
    s = 0 # s表示以a[i]结尾的最大连续子数组
    for i in range(1,n+1):
        s = max(0,s) + a[i]
        f[i] = max(f[i - 1],s)   # f[i-1]就表示不以a[i]为结尾了
    s = 0
    for i in range(n,0,-1):
        s = max(0,s) + a[i]
        g[i] = max(g[i + 1] , s)

    res = inf
    for i in range(1,n+1):
        res = max(res, f[i] + g[i+1])
    print(res)

28.涂色

具体代码如下

先将所有连通块变成一种颜色

n = int(input())
col = []
c = [int(x) for x in input().split()]
for i in range(len(c)):
    if i == 0:
        col.append(c[i])
    else:
        if c[i] == c[i-1]: continue
        else:
            col.append(c[i])
n = len(col)
col = [0] + col

dp = [[0]*(n+1) for _ in range(n+1)]
for lenn in range(2,n+1):
    for l in range(1,n + 2 - lenn):
        r = l + lenn - 1  
        if col[l] == col[r]:
            dp[l][r] = dp[l+1][r-1] + 1
        else:
            dp[l][r] = min(dp[l+1][r] , dp[l][r - 1]) + 1
print(dp[1][n])

## 参考自https://www.acwing.com/solution/content/69707/

具体为什么这种方法可以让所涉及的连通块包含开始操作选择的连通块，我也没有相同，可能他是一层一层的下去的？最后必定会设计到最底层的dp

29.叶子的颜色

看不懂题目，于是决定做一下没有上司的舞会，同样是用树形DP

29.没有上司的舞会

从BOSS往下找，f[u][i]就代表有u结点的快乐指数
假设j是u的儿子
f[u][1] 首先会 = happy[u]
f[u][1] += f[j][0]
f[u][0] += max(f[j][0],f[j][1])

具体代码如下

## 题目都看不懂，于是决定做一下 没有上司的舞会， 就代表刷这模块了

def dfs(u):  # 深度优先往下搜
    f[u][1] = happy[u]  # 有这个节点
    
    i = h[u]
    while i != -1:  # 找他的儿子
        j = e[i]
        dfs(j)
        f[u][1] += f[j][0]   # 有父节点
        f[u][0] += max(f[j][0],f[j][1])  # 没有父节点
        i = ne[i]
        


def add(a,b):  # b当a的儿子
    global idx
    e[idx] = b 
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

if __name__ == '__main__':
    N = 6010
    h,e,ne,idx = [-1]*N ,[0]*N, [-1]*N,0
    happy,f,has_fa = [0]*N,[[0]*2 for _ in range(N)], [False] * N
    n = int(input())
    for i in range(1,n+1):
        happy[i] = int(input())
    
    for i in range(n-1):
        a,b = map(int,input().split())
        add(b,a)
        has_fa[a] = True
    root = 1
    while has_fa[root] : root +=1 # 找到boss，就是没有父节点的
    dfs(root)
    print(max(f[root][0],f[root][1]))

30.最大上升子序列和

我的这种暴力BP应该会TLE，过不了全部的，但目前的水平就这样。。
记f[i] 表示以a[i]结尾的最大上升子序列和
遍历j从1到i
如果 a[j] < a[i]
f[i] = max(f[i], f[j] + a[i])
最后求max(f)就好了

具体代码如下

## 优先考虑暴力 BP 　肯定会TLE，但是先这样把，到时候复盘的时候如果想做再用树形DP
# f[i] 表示 以a[i] 结尾的 最大上升子序列和
# f[i] = f[j] + a[i]  1 <=j < i  a[j] < a[i]
N = 100010
n = int(input())
a = [0] + [int(x) for x in input().split()] 
f = [0] * N
for i in range(1,n + 1):
    f[i] = a[i]         #先加上自己
    for j in range(1,i):
        if a[i] > a[j]:
            f[i] = max(f[i] , f[j] + a[i])
print(max(f))

PS:31和32题都是拔高题，不是我能做的
到此为止啦