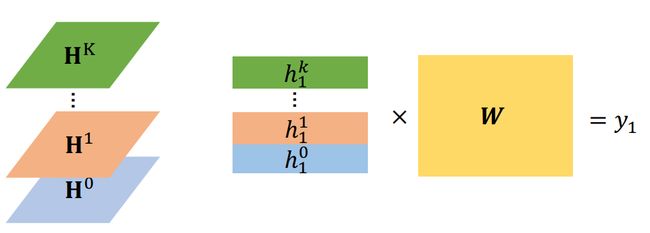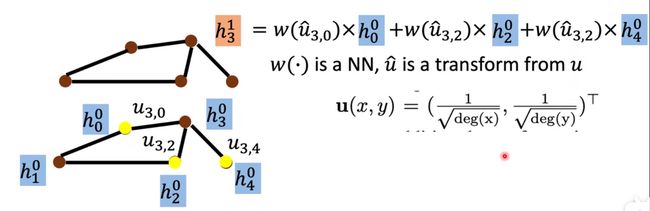图神经网络（CNN）四

图神经网络一 Graph Neural Network

写在前面：之前我是学过一些关于神经网络机器学习的内容的，但是因为写博客太麻烦了，所以学的时候就一直没有更新博客，但是后来因为有其他事情有接近两星期没有学习AI方面内容，结果今天发现之前学的AI都忘光了，所以最近开始写博客复习一下过去的内容。

本次博客涉及的图片均来自台湾大学的课件，如有侵权请联系我。

介绍

首先我们要知道图神经网络是个什么东西，我们从名字就可以看出来，Graph-Neural-Network，图-神经-网络，建立在图上的神经网络（再次之前建议先了解一下CNN，也就是卷积神经网络，建议去看吴恩达老师的机器学习的CNN课程，很简单的一个东西，10分钟就能看明白，当然你不想去看也没关系，我在下面也讲解了卷积的概念）

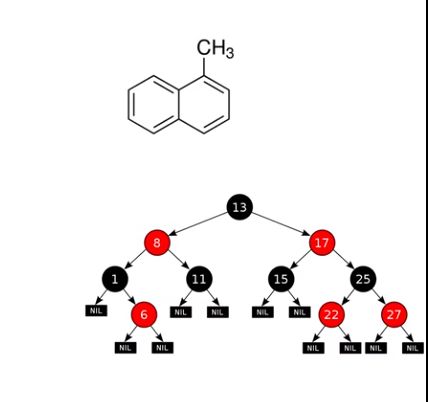
首先一个概念，什么是图，这个是一个数据结构的定义，我们在离散数学中也见过这个东西，就是连起来的不同节点，节点之间有一定的关系。比如我们高中经常看到的化学分子式，或者数据结构中的树。这些可以算是图。

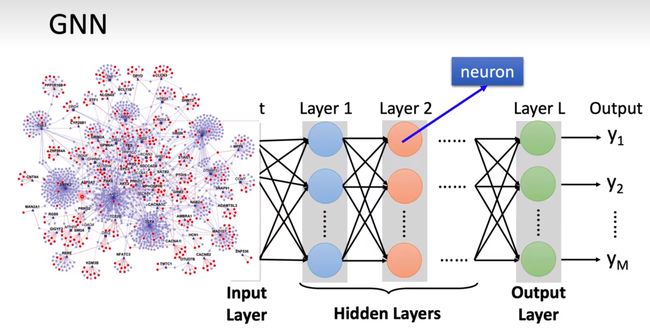
之前我们的神经网络都是建立在一个简单维度的数据集合上，比如我上一篇神经网络入门的那一篇中关于身高和体重的数据，这个数据只包含两个不相关的数据，而GNN，就是要把这些有关系的节点进行一个处理，然后使用神经网络的技术进行分析。就像下面这种情况。

CNN其实拥有很广泛的用处，因为图这种数据结构在我们的日常生活中其实很常见。我们就举一个简单的例子，这是我朋友目前在做的一个科研项目，就是通过图神经网络的技术来分析一个化学物质拥有什么样的属性。刚好台湾大学的课件也用到了这个例子，我就直接把这个课件截图过来了。

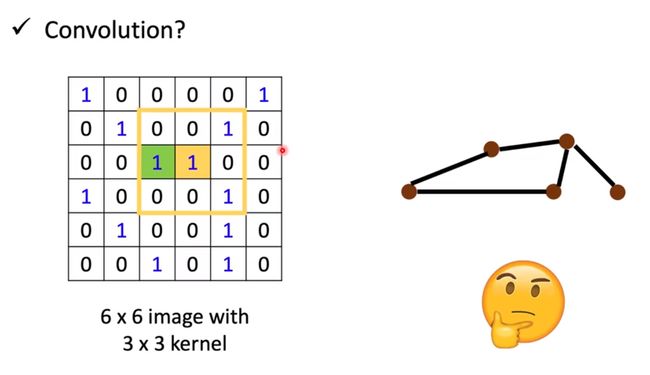
我们会发现图神经网络跟我们平常见到的神经网络最大的一个区别就是我们要考虑节点跟节点之间的关系，也就是一个节点邻居的影响，这种情况下我们一般会想到卷积这种运算方法，当然这里不是指信号与系统里面的卷积，不要害怕。这里的卷积指的是图卷积，就是CNN的那个卷积，但是问题来了，进行图片处理时的卷积，他要卷积的东西是一个规则的图形，所以使用起来很好理解，但是图神经网络是一个不规则的图形。这就是我们要面临的一个问题，如何在图上进行卷积操作。

Spatial-based GNN

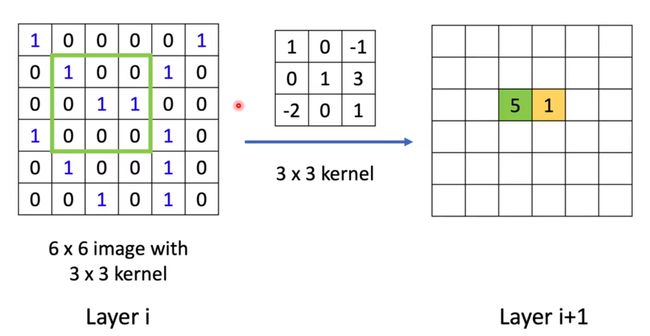
首先我们回忆一下什么是卷积。神经网络上的卷积其实就是简单的乘法和加法，我们会有一个卷积核，然后这个卷积核会与原来的矩阵进行一个相乘再相加（不是矩阵的乘法，就是相应位置的相乘，然后再加起来）

千言万语不如举个栗子：

我们看这个栗子

首先我们会有一个卷积核，就是右边的那个kernel，我们把这个框框框（框框-框，这是这三个字的断句）到左边的image图像（图像就是一个矩阵，你直接把图像理解成矩阵就可以）上，然后相重叠位置上的数相乘，然后再把这些加起来，比如这个就是1*1+1*1+1*3=5，然后再右边的位置填上5，填的位置就是这个卷积核中心所在的位置。然后我们把左边的卷积核右移，就可以得到下一个数，也就是黄色的那个1，这样我们把这个卷积核都走一遍，就算完成了一次卷积。

好，我们复习了卷积的概念之后，现在我们就要想如何对一个图进行一个卷积？这就是我们首先要讲的一个方法Spatial-based Convolution

我们还是借助台湾大学的课件。

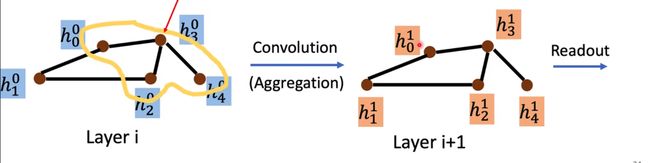
这一个刚开始看的话会有点懵，不过没关系，我会简单解释一下

首先我们讲一下这个具体的方法：

1. Aggregate：using neighbor feature update next hidden state.
2. Readout：gathering all the nodes’ feature to repesent the whole graph.

翻译一下就是

第一步我们首先利用一个节点的邻居节点来计算出这个节点下一层的权值。

第二步是通过某种方式把这些节点的权值计算成一个数，然后用这一个数来代表整个卷积后的图。

我们有四种方式可以得到这最后的结果，也就是最后Readout可以得到的$h_G$

NN4G

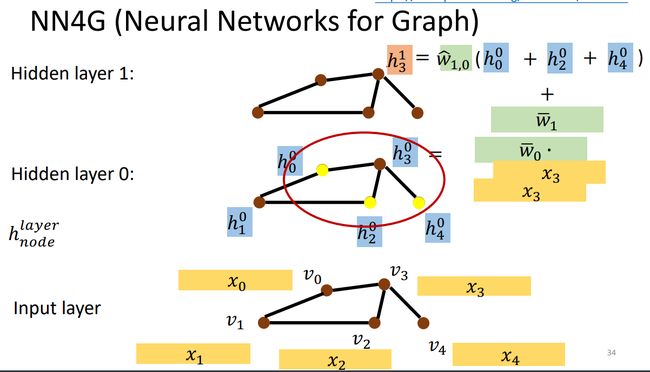
NN4G是Neural Networks for Graph的缩写，这是一个很简单的计算方法，做为一个神经网络，最重要的事情就是要进行一个update，我们需要不断对整个系统进行计算更新，迭代很多层之后，然后在readout，就可以得到我们需要的结果。

NN4G的更新方法也是很简单的，我们就是对于每个节点来说，只需考虑它当前的邻居节点，然后根据这个邻居节点计算这个节点下一层的权值，计算的方法也是很简单，就是将邻居节点相加然后加权相乘就可以了。

我们对台湾大学的课件进行一个解释把，$h_3^0$指的是第零层的第三个节点

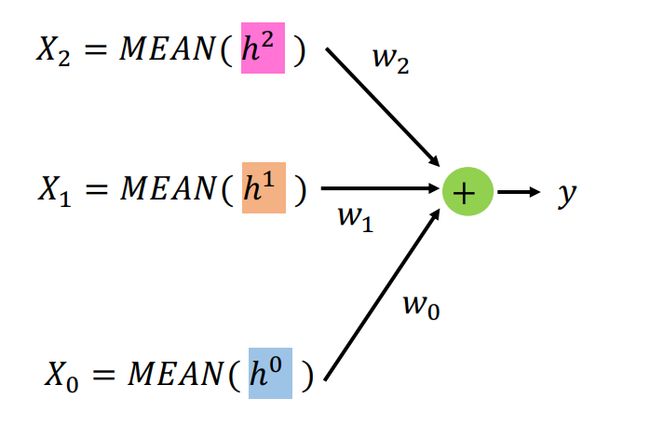
通过这种方法我们可以得到很多层神经网络，我们readout的结果也是更加简单，就是把每一层的节点求平均数，然后把所有层加权相乘，最后将每一层得到的结果相加就可以了，这样就可以得到最终的结果，而这些权值的计算方法是通过损失函数进行计算得到的。

有点懵逼是吗，这就对了，AI的力量来自玄学！

DCNN

DCNN的全称是Diffusion-Convolution Neural Network

这个的计算方法更加奇怪，但是AI有几个不奇怪的。。。

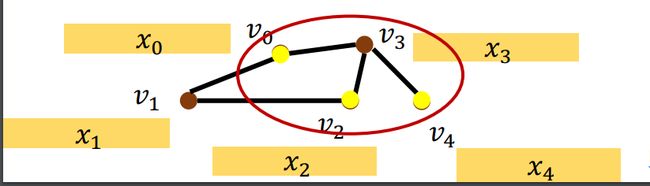
这个的update方式比较奇怪，它不是一层一层的去计算，按照我们之前对神经网络的传统理解，正常情况下来说上一层的输出是下一层的输入，但是这个情况下下一层的输入都只跟第一层有关，还是按台大的课件。

上图是我们最初的输入，我们利用这个去update神经网络

关于第一层的update，我们以v3几点为例，我们计算距离v3距离为1的节点，我们把这些节点（v0,v2,v4）相加然后乘以一个权值。

至于第二层update，我们还是以最初的一层为输入，不过这一次计算的是距离为2的节点的值，计算方法同第一层相同。

我们这样可以得到好几层的矩阵，这些矩阵都是由每一层节点的feasures构成的，我们就可以通过这些权值进行一个计算

我们就可以将这些权值进行一个矩阵的相乘就可以得到最终的feasures。

DGC

Diffusion Graph Convolution 这个是 ，更上一个基本一样，唯一的区别就是把$H^k到H^0$给加起来，然后就没了，就没了？？没错，就是这么简单（这个作者绝对是个水论文的，但肯定比我这个学术废物强）

MoNET

Mixture Model Networks.

这个神经网络和上面的不同点在于这个神经网络使用了边的一个权值，也就是考虑到了边对不同节点之间权值的影响。

这个地方具体还是建议去直接看相关论文，我只是做一个简单介绍。

GraphSAGE

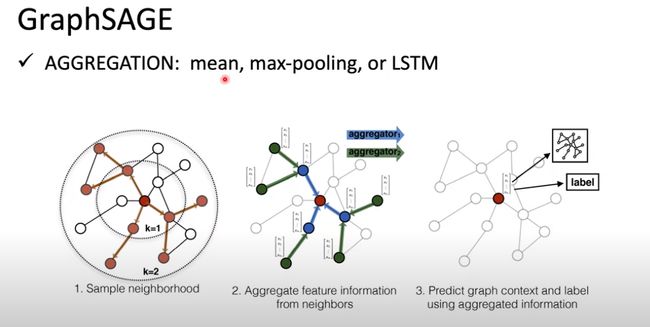
SAmple and aggreGatE:简称GraphSAGE

主要的地方就是他的一个aggregation:包括mean,max-pooling,or LSTM

pooling这个概念就是卷积神经网络的那个pooling。

这个模型我也不是特别明白，这个东西以后有时间会进行更新

GAT

Graph Attention Networks

GAT是一个比较常用的神经网络

对邻居做attention，我们会有一个函数来计算点与点之间的weight，也就是图中的e参数。

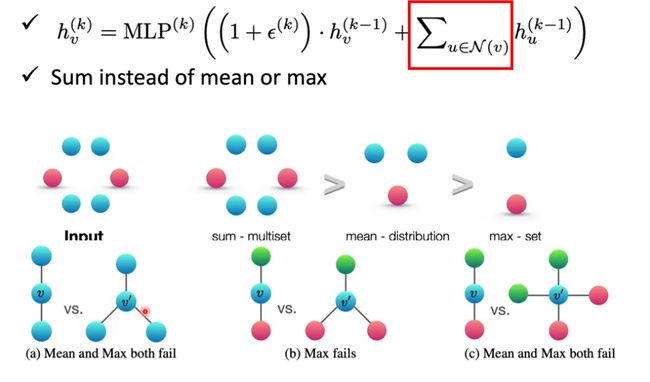
GIN

这一个给出了一个理论的证明

而且还有一个问题就是图中红色方框的地方，红色方框里面的公式代表的是我们要把邻居的节点给加起来，

这个前一项的意思是我们应该加上一个参数乘以之前一层的节点值，然后进行一个处理就可以了。

至于为什么我们要进行相加而不是平均，因为我们需要将两种图给分开，就像最下面的a图，如果相加的话我们可以将两种图片给区分开来，要不然就没法区分完了大蛋。

小结

这篇博客我简单介绍了一些常用的图神经网络，下一篇博客会介绍更加深入的内容

希望这篇博客能够帮助到你