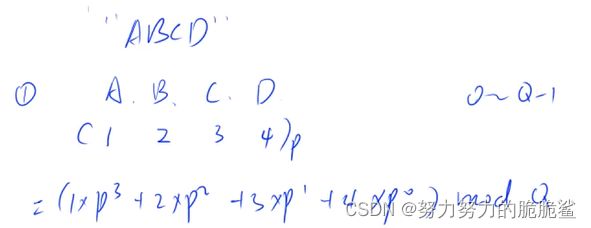【算法基础9】c/c++中如何构建哈希表?字符串哈希其实很简单
一、构建哈希表的基本思路
哈希表主要是为了将较大范围的数映射到一个较小的范围,与离散化有些类似,但离散化映射后的数仍然保持数与数之间的顺序,而哈希表中数的顺序是打乱的。哈希表的映射方法主要是将大范围的数对N取模,但可能存在多个数取模后的值相同,这样就产生了冲突。为了减少冲突,N通常取质数,根据解决冲突的方式不同,哈希表的构建又分拉链法和开放寻址法两种。
查找第一个大于N的质数:
//为了减少冲突,求哈希取模的数最好是质数
int prime(int n){
for(int i=n;;i++){
bool flag=true;
for(int j=2;j*j二、拉链法
主要思想:哈希表的每个槽位充当链表的头结点,将产生冲突的数依次链接上去,使得哈希表呈现“拉链状”,能够实现“一对多”。
例题:给出n行操作,“I x”表示在哈希表中插入数x,“F x”表示在哈希表中查找数x,如果x存在则打印“YES”,否则打印“NO”。
#include
#include
using namespace std;
const int N=23;
int h[N],e[N],ne[N],idx;
void insert(int x){
int k=(x%N+N)%N;//负数取模后是负数,加上N后再取一次模保证为正数
e[idx]=x;//同数组模拟链表,详见【算法基础6】
ne[idx]=h[k];
h[k]=idx++;
}
bool find(int x){
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i]){//沿着链表进行查找
if(e[i]==x) return true;
}
return false;
}
int main(){
int n,x;
char op[2];
scanf("%d",&n);
memset(h,-1,sizeof h);//将哈希表初始化,注意memset是按字符进行赋值
while(n--){
scanf("%s %d",op,&x);
if(*op=='I') insert(x);
else{
if(find(x)) printf("YES\n");
else printf("NO\n");
}
}
return 0;
} 三、开放寻址法
主要思想:当前槽位已经有数存储的时候,查找下一个槽位,直到找到空槽位为止。
例题:给出n行操作,“I x”表示在哈希表中插入数x,“F x”表示在哈希表中查找数x,如果x存在则打印“YES”,否则打印“NO”。
#include
#include
using namespace std;
const int N=23,null=0;//null不在输入范围即可
int h[N];
int find(int x){//开放寻址法的核心操作
int k=(x%N+N)%N;
while(h[k]!=null&&h[k]!=x){//当前槽位已经有其他数存在
k++;
if(k==N) k=0;//走到尽头,回到k的前面查找
}
return k;
}
int main(){
int n,x;
char op[2];
scanf("%d",&n);
memset(h,0,sizeof(h));
while(n--){
scanf("%s %d",op,&x);
int k=find(x);
if(*op=='I') h[k]=x;
else{
if(h[k]!=null) printf("YES\n");
else printf("NO\n");
}
}
return 0;
} 四、字符串前缀和哈希
主要思想:
采用P进制的方法把字符串映射成数字,再像普通哈希的一样将映射后的数字对Q取模,构成哈希表。为了减少冲突,通常将P取为131或者13331,将Q取为2的64次方。在实际应用中可用将哈希表的数据类型定义为unsigned long long,溢出的过程相当于取模,能够减少代码。
同数字前缀和数组类似,字符串前缀和数组h[]可以由公式h[i]=h[i-1]*P+str[i]构建,求一段区间【l,r】上的字符串对应的哈希数可以由公式h[r]-h[l-1]*p[r-l+1]得到,其中p[]是为了化简运算,提前构建的P的次方数组。这样就可以在O(1)时间内判断两个字符串是否相等。
例题:给出一个长度为n的字符串str,求m个操作,每次判断区间【l1,r1】和【l2,r2】的字符串是否相等,如果相等则输出“YES”,否则输出“NO”。
#include
using namespace std;
const int N=10010,P=131;
typedef unsigned long long ULL;//typedef提前定义简化代码
ULL p[N],h[N];//p为P的次方数组,h为前缀和哈希数组
ULL get(int l,int r){
return h[r]-h[l-1]*p[r-l+1];//返回一个区间段内字符串对应的数
}
int main(){
int m,n;
char str[N];
scanf("%d %d %s",&n,&m,str+1);//循环里i从1开始,字符串存储也要从1开始
p[0]=1,h[0]=0;
for(int i=1;i<=n;i++){
p[i]=p[i-1]*P;//p[i]存储的是P的i次方
h[i]=h[i-1]*P+str[i];//求前缀和
}
while(m--){
int l1,r1,l2,r2;
scanf("%d %d %d %d",&l1,&r1,&l2,&r2);
if(get(l1,r1)==get(l2,r2)) printf("YES\n");
else printf("NO\n");
}
return 0;
}