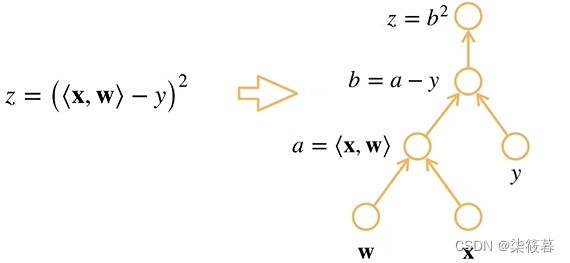【深度学习】PyTorch基础入门（爆肝2万字）

【深度学习】PyTorch基础入门

预备：

本文章内容使用李沐老师著作的《动手学深度学习PyTorch版》作为教材。

教材在线电子书：https://zh.d2l.ai/index.html

教材离线电子书：

      中文版：点击获取

      英文版：点击获取

纸质书购买链接：点击跳转

BiliBili课程链接：点击跳转

本文代码下载：点击跳转

前往https://www.angie.js.cn/index.php/archives/717.html可下载JupyterNotebook版笔记文档。

1 PyTorch的历史发展

PyTorch于2017年首次提出，它是由FaceBook根据流行的Torch框架开发的。而在这之前，深度学习领域由TensorFlow占据主导地位，老牌深度学习框架TensorFlow是由谷歌旗下的Google Brain团队于2015年首次开发，而在15年之前则由更老牌的Caffe占据半壁江山。不过在这几年里，PyTorch的使用者明显增多，根据谷歌指数与百度指数的搜索关键字分析，TensorFlow的搜索热度正逐年下降，而PyTorch则逐年上升，目前PyTorch的搜索热度已经连续多年超过TensorFlow，可见PyTorch也会是未来几年中广大开发者们流行使用的深度学习框架。

正所谓"长江后浪推前浪，一代更比一代强"，PyTorch究竟为何能够超越老牌深度学习框架还是有很多原因的，其中之一就是学习成本更低，PyTorch最初是NumPy的高级替代品，所以它的使用方法在很多地方都是与NumPy相通的，只要你掌握了NumPy的基本使用，再去学习PyTorch都将是非常容易的，而恰巧对于数据科学家以及AI工程师，在学习机器学习的时候就已经接触到了NumPy。

到了今日，深度学习领域所流传的三大深度学习框架——TensorFlow，PyTorch以及Keras，不过Keras更像是一个神经网络模型库，几乎不提供数值计算的功能，并且底层是由TensorFlow进行封装，所以在深度学习领域还是由TensorFlow和PyTorch平分秋色。近年来国内对于深度学习的发展也有很大进步，知名的深度学习框架有由百度主导开发的飞桨（PaddlePaddle, https://www.paddlepaddle.org.cn/），这是中国首个自主研发、功能完备、开源开放的产业级深度学习平台，也是很多中国公司所使用的深度学习框架。

如果想要深入了解飞桨，可以学习《动手学深度学习PaddlePaddle版》，课程链接https://aistudio.baidu.com/aistudio/course/introduce/25851。

2 PyTorch的安装

PyTorch的安装可以参考PyTorch官网(https://pytorch.org/)，点击转到Get Started页面，选择配置，如果你有一块NVIDIA独立显卡并且性能还不错，可以尝试安装GPU版本以提高模型训练效率，如果安装GPU版本的PyTorch，则还需要先安装CUDA，并且确保CUDA的版本与配置上的版本一致。CUDA下载地址为：https://developer.nvidia.com/cuda-toolkit-archive，选择与之对应的版本下载安装，如果不知道自己的电脑是否安装CUDA，可以在cmd中输入nvidia-smi命令查看，一般英伟达显卡都会自带CUDA。图中演示为PyTorch的CPU版本。

复制Run this Command行对应的内容，使用pip命令一键安装，由于整个框架体量非常大（占用磁盘空间在2GB以上)，对于CPU版本，如果是从pypi下载将会很慢，建议使用镜像源安装，GPU版本只能在PyTorch官网指定的下载源下载wheel文件来安装，用不用镜像源都无所谓。CPU版本我这里使用的是清华镜像源，具体命令如下：

# GPU版本，CUDA版本为11.7的环境下
pip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu117

# CPU版本，不需要安装CUDA
pip3 install torch torchvision torchaudio -i https://pypi.tuna.tsinghua.edu.cn/simple

安装完成后，打开cmd，输入python进入Python运行环境，导入PyTorch，查看PyTorch版本已验证是否安装成功。导入不报错并且输入版本号则表示安装完成。

python

import torch
torch.__version__

一、数据操作

1.1 基本操作对象

PyTorch操作的基本对象是张量。张量表示一个由数值组成的数组，这个数组可能有多个维度（轴）。具有一个轴的张量对应数学上的向量（vector），具有两个轴的张量对应数学上的矩阵（matrix），具有两个以上轴的张量没有特定的数学名称。这有些类似于NumPy中的数组，不过在NumPy中更倾向于表示为n维数组，有几维就叫做几维数组。NumPy对于这种多维的数据结构更倾向于用计算机的名词来命名，而PyTorch则更倾向于使用数学名词来命名，这或许也就是PyTorch比NumPy更加高级的原因，毕竟计算机乃至AI本来也就是在数学的基础上发展的。

我们可以使用arange来创建一个行向量x。这里要注意的是，我们在导入PyTorch时，import进来的是torch，而不是pytorch。

import torch

x = torch.arange(12)
x

PyTorch中的arange函数和NumPy的arange函数使用方式大致相同，PyTorch中的arange函数也具有三个参数start、end和step，使用arange函数生成2~12之间取步长为2的所有数字组成的行向量x1，arange和大多数生成序列的规则相同，即为左闭右开，end所指定的值不会被取到。

x1 = torch.arange(2, 12, 2)
x1

使用张量的shape属性可以访问张量在每个轴上的长度，也就是形状（shape），同样和NumPy很相似。

x.shape

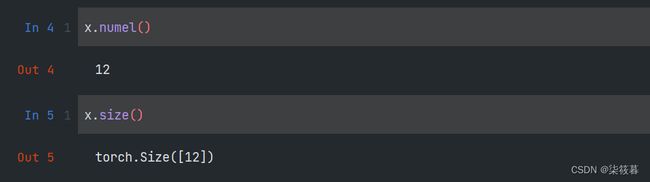
如果想知道张量的所有元素的总数，也就是张量所有维度上的长度的乘积，不再考虑张量的维度，可以使用张量的numel方法，这时返回的是一个数值，也可以使用size方法，不过不同的是这时返回的是一个维度信息。

x.numel()
x.size()

使用reshape函数可以修改张量的维度，也就是改变形状，当某个维度指定为-1时，则该维度的长度将由计算机根据其他已经传入的维度长度自动计算并给出，和NumPy中reshape方法的使用大致相同。要注意的是使用reshape方法并不会修改原来的张量，而是返回一个新的张量，所以需要使用一个变量来接收。

x.reshape(2, 6)
x.reshape(-1, 4)

有时我们想要使用全0、全1、其他常量或者从特定分布中随机采样的数字来初始化矩阵。可以使用zeros生成全0张量，使用ones生成全1张量，只需传入一个包含生成张量维度信息的可迭代对象即可得到。

torch.zeros((2, 3, 4))
torch.ones((2, 3, 4))

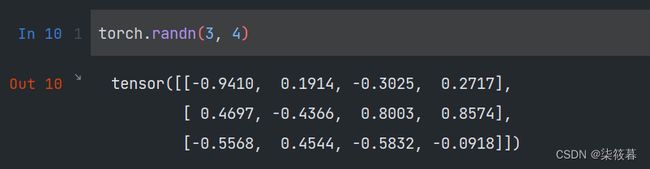
有时我们想要通过从某个特定的概率分布中随机采样来得到张量中每个元素的值。例如，当我们构造数组来作为神经网络中的参数时，我们通常会随机初始化参数的值。使用randn函数创建一个形状为(3, 4)的张量。其中的每个元素都从均值为0、标准差为1的标准正态分布（高斯分布）中随机采样。

torch.randn(3, 4)

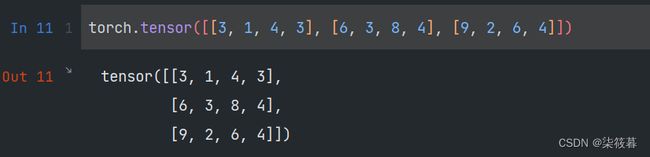
与NumPy具有相同的功能，我们也可以将Python中的列表或嵌套列表转化为PyTorch中的张量，外层的列表对应着张量的第一维，即轴0，第二层对应着第二维，即轴1，以此类推。

torch.tensor([[3, 1, 4, 3], [6, 3, 8, 4], [9, 2, 6, 4]])

1.2 运算符

数据操作自然离不开数学运算，其中最简单且最有用的操作是按元素（elementwise）运算。常见的标准算术运算符（+、-、*、/和**）都可以被升级为按元素运算。在PyTorch中，我们可以将形状相同的两个张量进行标准算术运算符操作。

x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([1, 2, 3, 4])

x + y, x - y, x * y, x / y, x ** y # **运算符是求幂运算

“按元素”方式可以应用于更多的计算，包括像求幂这样的一元运算符。

torch.exp(x)

我们也可以把多个张量拼接在一起，把它们端对端地叠起来形成一个更大的张量。使用cat函数可以实现这个操作，指定维度可以实现是按哪一个轴进行拼接，示例中X、Y均为3行4列张量，按dim=0进行拼接得到6行4列张量，按dim=1进行拼接得到3行8列张量，所以按哪个轴拼接其实也就是在将所有要拼接的张量在这个轴上的长度进行相加。

X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)

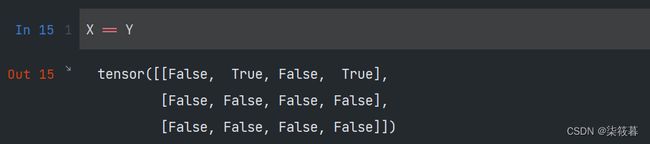
和NumPy一样，PyTorch也支持“按元素”逻辑运算，最简单的是比较两个张量对应位置元素值是否相等，即X == Y。对于每个位置，如果X和Y在该位置相等，则新张量中对应项的值为True，这意味着逻辑语句X == Y在该位置处为True，否则为False。

X == Y

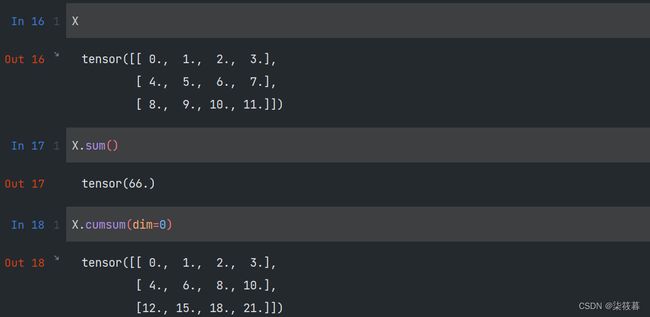
对张量中的所有元素求和，使用sum方法会产生一个单元素张量。使用cumsum方法，会计算元素的累和，并将每次累和的结果构成与原来维度相同的一个张量。如果张量是多维的，则在计算时需要传入dim参数指定在哪个轴上进行累和操作。

X
X.sum()
X.cumsum(dim=0)

1.3 广播机制

在某些情况下，即使形状不同，我们扔然可以通过调佣广播机制（broadcasting mechanism）来执行按元素操作。这种机制的工作方式如下：

（1）通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状；

（2）对生成的数组执行按元素操作。

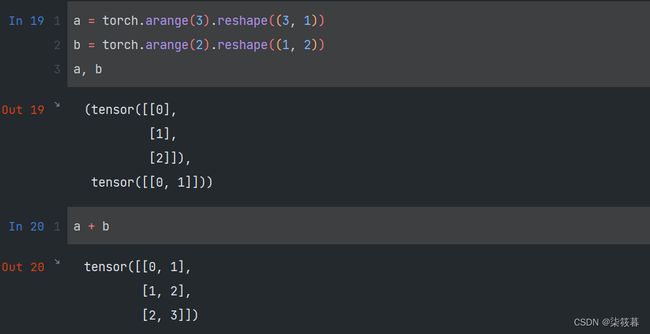
在大多数情况下，我们将沿着数组中长度为1的轴进行广播。由于a和b分别是3x1矩阵和1x2矩阵，如果让它们相加，它们的形状不匹配。我们将两个矩阵广播为一个更大的3x2矩阵，矩阵a将复制列，矩阵b将复制行，然后按元素相加。这和NumPy中的广播机制相同。

a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b

a + b

1.4 索引和切片

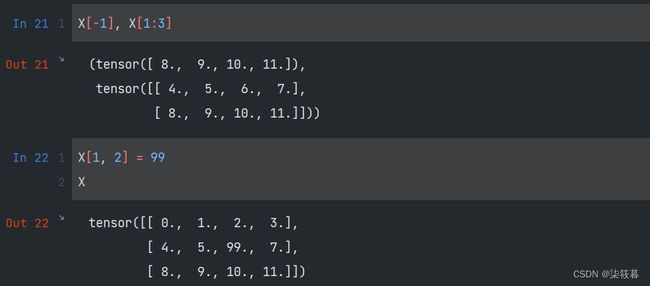
和NumPy一样，PyTorch同样支持通过索引访问张量中的元素。同时可以指定范围访问指定区域的元素，第一个元素的索引是0，最后一个元素的索引是-1。除此之外，还可以通过对指定索引赋值来改变原来张量中的元素。

X[-1], X[1:3]

X[1, 2] = 99
X

如果我们想为多个元素赋予相同的值。我们只需要索引所有元素，然后为它们赋值。

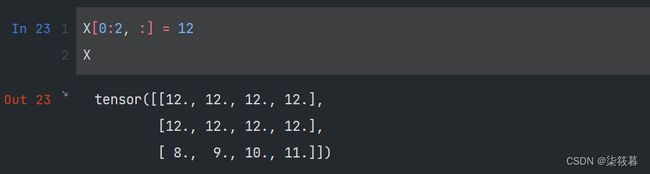
X[0:2, :] = 12
X

1.5 对象转换

PyTorch可以将深度学习框架定义的张量随时转换为NumPy中的ndarray，反之亦是如此。torch张量和numpy数组将共享它们的底层内存。

A = X.numpy()  # tensor转换成ndarray
B = torch.tensor(A)  # ndarray转换成tensor

type(A), type(B)

要将大小为1的张量转换为Python标量，可以调用item函数或使用Python的内置函数强转，对于大小大于1的张量（向量和矩阵），可以使用tolist函数将其转换成Python中的列表或嵌套列表。

a = torch.tensor([3.5])
b = torch.tensor([2, 4, 6])

a, b

a.item(), b.tolist()

float(a), int(a)

二、线性代数

2.1 标量

在对矩阵进行运算时，不可避免的需要使用到线性代数的知识。仅包含一个数值被称为标量（scalar），比如要将华氏温度值转换为摄氏温度值，可以通过公式$c=\frac{5}{9}(f-32)$，在此公式中，5、9和32是标量值，符号c和f称为变量（variable），它们表示未知的标量值。

标量由只有一个元素的张量表示，可以对标量进行常规的加减乘除和指数运算。以下是创建两个标量x,y，并将其进行一些简单的算术运算。

import torch

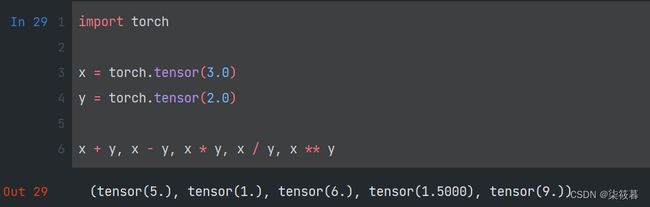
x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x - y, x * y, x / y, x ** y

2.2 向量

向量可以被视为标量值组成的列表，这些标量值被称为向量的元素（element）或分量（component）。比如20个人的年龄可以组成向量。在数学上，具有一个轴的张量表示向量。一般来说，张量可以具有任意长度，这取决于机器的内存限制。

x = torch.arange(4)
x

在数学中，向量x可以写为：

x = [ 0 1 2 3 ] x=\begin{bmatrix} 0 \\ 1 \\ 2 \\ 3 \end{bmatrix} x= ​0123​ ​

我们可以使用下标来引用向量的任一元素或查看元素值。可以通过使用len函数查看向量的长度，同时也可以使用shape属性得到向量的形状。

x[3], len(x), x.shape

2.3 矩阵

向量是将标量从零阶推广到一维，矩阵则是将向量从一维推广到二维。矩阵通常用粗体、大写字母来表示（例如，X、Y和Z），在代码中表示为具有两个轴的张量。

在数学上，矩阵使用$\mathbf{A}\in {\mathbb{R}}^{m\times n}$来表示矩阵A，其实也就是由m行n列的实数标量组成，我们可以将任意矩阵$A\in {\mathbb{R}}^{m\times n}$视为一个表格，其中每个元素$a_{ij}$属于第i行第j列：

A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ ⋮ a 41 a 42 … a m n ] A=\begin{bmatrix} a_{11}\quad a_{12}\quad\ldots\quad a_{1n} \\ a_{21}\quad a_{22}\quad\ldots\quad a_{2n} \\\vdots\quad\vdots\quad\quad\quad\vdots \\ a_{41}\quad a_{42}\quad\ldots\quad a_{mn} \end{bmatrix} A= ​a11​a12​…a1n​a21​a22​…a2n​⋮⋮⋮a41​a42​…amn​​ ​

对于任意$A\in {\mathbb{R}}^{m\times n}$，A的形状是(m, n)或mxn。当矩阵具有相同数量的行和列时，其形状变为正方形，因此，它被称为方阵（square matrix）。
当调用函数来实例化张量时，我们可以通过指定两个分量m和n来创建一个形状为mxn的矩阵。

A = torch.arange(20).reshape(5, 4)
A

我们可以通过行索引(i)和列索引(j)来访问矩阵中的标量元素$a_{ij}$，例如$[A{]}_{ij}$。

A.T

当我们交换矩阵的行和列时，结果称为矩阵的转置（transpose）。通常用$A^T$来表示矩阵的转置，如果$B=A^T$，则对于任意i和j，都有$b_{ij}=a_{ij}$，也就是两个矩阵对应元素值相等。作为方阵的一种特殊类型，对称矩阵（symmetric matrix）A等于其转置：$A=A^T$。

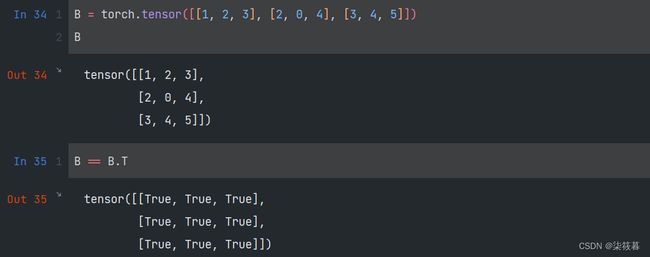
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B

B == B.T

2.4 张量

矩阵是将向量从一维推广到二维，而张量则是在更高维上的推广，这样我们就可以构建具有更多轴的数据结构。不过要注意的是，这里所说的张量并不是PyTorch里所定义的张量，而是数学当中的张量，也就是代数对象。其实在某种程度上，向量和矩阵也可以叫做张量，向量是一阶张量，矩阵是二阶张量。

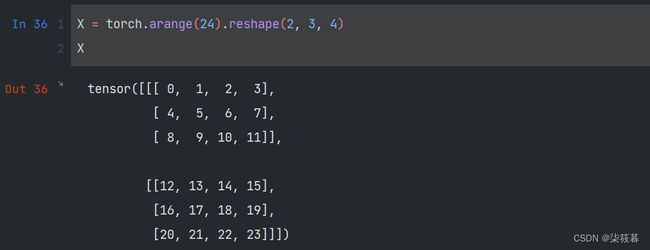
X = torch.arange(24).reshape(2, 3, 4)
X

2.5 张量的基本运算

标量、向量、矩阵和任意数量轴的张量可以进行一些简单的运算。给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量。比如，将两个相同形状的矩阵相加，会在这两个矩阵上执行元素加法。

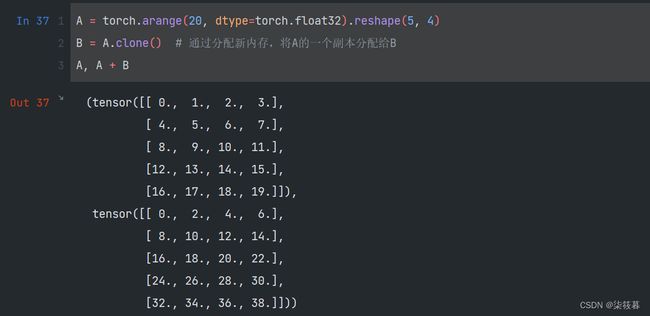
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

也可以对两个矩阵进行按元素乘法，这也叫做哈达玛积（Hadamard product）（数学符号$\odot$）。对于矩阵$B\in {\mathbb{R}}^{m\times n}$，其中第i行第j列的元素是$b_{ij}$。则矩阵A和B的哈达玛积为：

A ⊙ B = [ a 11 b 11 a 12 b 12 … a 1 n b 1 n a 21 b 21 a 22 b 22 … a 2 n b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 b m 1 a m 2 b m 2 … a m n b m n ] A\odot B=\begin{bmatrix}a_{11}b_{11}\quad a_{12}b_{12}\quad\ldots\quad a_{1n}b_{1n} \\a_{21}b_{21}\quad a_{22}b_{22}\quad\ldots\quad a_{2n}b_{2n} \\\vdots\quad\vdots\quad\ddots\quad\vdots \\a_{m1}b_{m1}\quad a_{m2}b_{m2}\quad\ldots\quad a_{mn}b_{mn}\end{bmatrix} A⊙B= ​a11​b11​a12​b12​…a1n​b1n​a21​b21​a22​b22​…a2n​b2n​⋮⋮⋱⋮am1​bm1​am2​bm2​…amn​bmn​​ ​

A * B

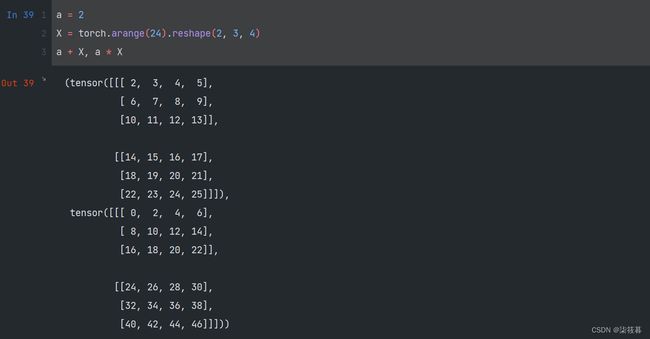
将张量加上或乘以一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, a * X

2.6 聚合

我们可以对任意张量进行的一个有用的操作是计算其元素的和。数学上使用符号$\sum$表示求和，为了表示长度为d的向量中元素的总和，可以记为$\sum _{i=1}^d{x}_i$。在矩阵中则使用$\sum _{i=1}^m\sum _{j=1}^n{a}_{ij}$来表示。

x = torch.arange(4, dtype=torch.float32)
x, x.sum()

A.shape, A.sum()  # 矩阵A的求和

在矩阵中，还可以通过指定axis来对某一轴上的元素求和，指定axis=0时将通过对所有行的元素来求和，指定axis=1时将通过对所有列的元素来求和。

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

除了求和外，还可以对张量求平均值（mean或average）。同样的，也支持按指定轴对元素求均值。

A.mean(), A.sum() / A.numel()

A.mean(axis=0), A.sum(axis=0) / A.shape[0]

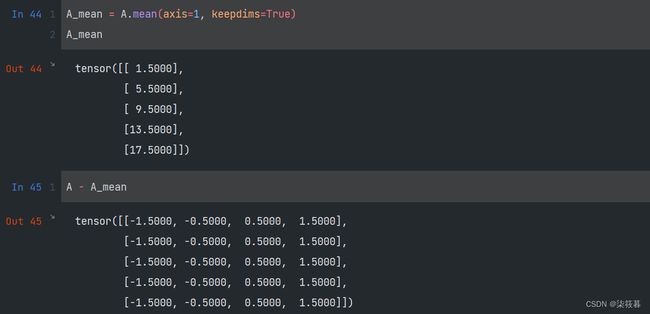
有时候，保持原来的轴数不变是很有必要的，例如，在求模型评判指标均方误差（Mean Square Error,MSE）时，需要计算每个样本数据的特征与其对应的特征的平均值的差作为模型误差。在求得均值后，利用广播机制计算每个特征存在的误差。

A_mean = A.mean(axis=1, keepdims=True)
A_mean

A - A_mean

2.7 点积

给定两个向量$x,y\in {\mathbb{R}}^d$，它们的点积（dot product）$x^{T}y$或（）。是相同位置的按元素乘积的和：$x^{T}y=\sum _{i=1}^d{x}_i{y}_i$。其实也就是哈达玛积得到的张量再进行求和。

y = torch.ones(4, dtype=torch.float32)
x, y, torch.dot(x, y)

torch.sum(x * y)

2.8 矩阵-向量积

回顾上面所定义的矩阵$A\in {\mathbb{R}}^{m\times n}$和向量$x\in {\mathbb{R}}^n$。对于矩阵A我们可以表示成：

A = [ a 1 T a 2 T ⋮ a m T ] A=\begin{bmatrix}a_1^T\\a_2^T\\\vdots\\a_m^T\end{bmatrix} A= ​a1T​a2T​⋮amT​​ ​

其中，每个$a_i^T\in {\mathbb{R}}^n$都是行向量，表示矩阵的第i行。矩阵向量积$Ax$是一个长度为m的列向量，其第i个元素是点积$a_i^{T}x$：

A x = [ a 1 T a 2 T ⋮ a m T ] x = [ a 1 T x a 2 T x ⋮ a m T x ] Ax=\begin{bmatrix}a_1^T\\a_2^T\\\vdots\\a_m^T\end{bmatrix}x=\begin{bmatrix}a_1^Tx\\a_2^Tx\\\vdots\\a_m^Tx\end{bmatrix} Ax= ​a1T​a2T​⋮amT​​ ​x= ​a1T​xa2T​x⋮amT​x​ ​

我们可以把一个矩阵$A\in {\mathbb{R}}^{m\times n}$乘法看作从${\mathbb{R}}^n$到${\mathbb{R}}^m$向量的转换。在PyTorch中，我们可以使用mv函数来计算得到矩阵和向量的矩阵-向量积（matrix-vector product）。不过要注意的是，矩阵A在列上的长度必须与x的长度相同。

torch.mv(A, x)

2.9 矩阵-矩阵乘法

假设有两个矩阵$A\in {\mathbb{R}}^{n\times k}$和$B\in {\mathbb{R}}^{k\times m}$：

A = [ a 11 a 12 … a 1 k a 21 a 22 … a 2 k ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 … a n k ] ， B = [ b 11 b 12 … b 1 m b 21 b 22 … b 2 m ⋮ ⋮ ⋱ ⋮ b k 1 b k 2 … b k m ] A=\begin{bmatrix}a_{11}\quad a_{12}\quad\ldots\quad a_{1k} \\ a_{21}\quad a_{22}\quad\ldots\quad a_{2k} \\\vdots\quad\vdots\quad\ddots\quad\vdots \\ a_{n1}\quad a_{n2}\quad\ldots\quad a_{nk}\end{bmatrix}， B=\begin{bmatrix}b_{11}\quad b_{12}\quad\ldots\quad b_{1m} \\ b_{21}\quad b_{22}\quad\ldots\quad b_{2m} \\\vdots\quad\vdots\quad\ddots\quad\vdots \\ b_{k1}\quad b_{k2}\quad\ldots\quad b_{km}\end{bmatrix} A= ​a11​a12​…a1k​a21​a22​…a2k​⋮⋮⋱⋮an1​an2​…ank​​ ​，B= ​b11​b12​…b1m​b21​b22​…b2m​⋮⋮⋱⋮bk1​bk2​…bkm​​ ​

用行向量$a_i^T\in {\mathbb{R}}^k$表示矩阵A的第i行，并用列向量$b_j\in {\mathbb{R}}^k$表示矩阵B的第j列。要生成矩阵积$C=AB$，最简单的方法是考虑$A$的行向量和$B$的列向量：

A = [ a 1 T a 2 T ⋮ a n T ] ， B = [ b 1 b 2 ⋯ b m ] A=\begin{bmatrix}a_1^T\\a_2^T\\\vdots\\a_n^T\end{bmatrix}，B=\begin{bmatrix}b_1\quad b_2\quad\cdots\quad b_m\end{bmatrix} A= ​a1T​a2T​⋮anT​​ ​，B=[b1​b2​⋯bm​​]

当我们简单地将每个元素$c_{ij}$计算为点积$a_i^T{b}_j$：

C = A B = [ a 1 T a 2 T ⋮ a n T ] [ b 1 b 2 ⋯ b m ] = [ a 1 T b 1 a 1 T b 2 … a 1 T b m a 2 T b 1 a 2 T b 2 … a 2 T b m ⋮ ⋮ ⋱ ⋮ a n T b 1 a n T b 2 … a n T b m ] C=AB=\begin{bmatrix}a_1^T\\a_2^T\\\vdots\\a_n^T\end{bmatrix}\begin{bmatrix}b_1\quad b_2\quad\cdots\quad b_m\end{bmatrix}=\begin{bmatrix}a_1^Tb_1\quad a_1^Tb_2\quad\ldots\quad a_1^Tb_m \\ a_2^Tb_1\quad a_2^Tb_2\quad\ldots\quad a_2^Tb_m \\\vdots\quad\vdots\quad\ddots\quad\vdots \\ a_n^Tb_1\quad a_n^Tb_2\quad\ldots\quad a_n^Tb_m\end{bmatrix} C=AB= ​a1T​a2T​⋮anT​​ ​[b1​b2​⋯bm​​]= ​a1T​b1​a1T​b2​…a1T​bm​a2T​b1​a2T​b2​…a2T​bm​⋮⋮⋱⋮anT​b1​anT​b2​…anT​bm​​ ​

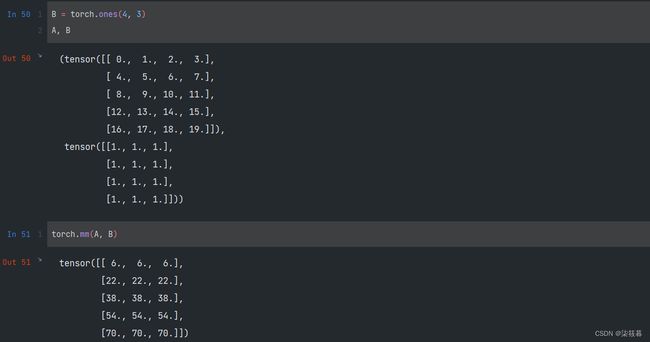
我们把矩阵-矩阵乘法$AB$看作简单地执行m次矩阵-向量积，并将结果拼接在一起，得到一个$n\times m$矩阵。在PyTorch中，我们可以使用mm函数来计算得到两个矩阵的矩阵-矩阵乘法（matrix-matrix multiplication）。矩阵乘法与哈达玛积不同，应避免混淆。

B = torch.ones(4, 3)
A, B

torch.mm(A, B)

2.10 范数

在线性代数中，向量范数（norm）是将向量映射到标量的函数f。给定任意向量x，向量范数通常具有以下性质：

1. 如果我们按常数因子α缩放向量的所有元素，其范数也会按相同常数因子的绝对值缩放：$f(\alpha x)=|\alpha |f(x)$
2. 范数遵循三角形不等式：$f(x+y)\le f(x)+f(y)$
3. 范数必须是非负的：$f(x)\ge 0$
4. 要求范数最小为0，则当且仅当向量全由0组成：$\forall i,[x{]}_i=0\iff f(x)=0$

范数很像距离的度量，事实上，欧几里得距离是一个$L_2$范数：假设n维向量x中的元素是$x_i，x_2，\cdots ，x_n$，其$L_2$范数是向量元素平方和的平方根：

$${\Vert x\Vert }_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$

其中，在$L_2$范数中常常省略下标2，也就是说$||x||$等同于$||x|{|}_2$。

u = torch.tensor([3.0,  -4.0])
torch.norm(u)

除了$L_2$范数，我们还经常在深度学习中遇到$L_1$范数，$L_1$范数表示为向量内元素的绝对值之和：

$${\Vert x\Vert }_1=\sum _{i=1}^n|x_i|$$

torch.abs(u).sum()

$L_2$范数和$L_1$范数都是更一般的$L_p$范数的特例：

$${\Vert x\Vert }_p=(\sum _{i=1}^n|x_i{|}^p{)}^{\frac{1}{p}}$$

类似于向量的L_2范数，矩阵$X\in {\mathbb{R}}^{m\times n}$的弗罗贝尼乌斯范数（Frobenius norm）是矩阵内元素平方和的平方根：

$${\Vert X\Vert }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{x}_{ij}^2}$$

弗罗贝尼乌斯范数具有向量范数的所有性质，它就像是矩阵行向量的$L_2$范数。以下是计算弗罗贝尼乌斯范数的一个例子。

torch.norm(torch.ones((4, 9)))

三、微积分

3.1 导数和微分

在深度学习中，如果我们需要使模型得到一个相对较好的结果，我们需要引入损失函数（lost function），即一个衡量“模型有多糟糕”这个问题的分数。要使得模型的损失函数最小，通常需要求得在目标函数的斜率为0的情况下所对应的在各个轴上的系数，而这一步骤的实现就需要通过求导来完成。

假设有一个函数$f:\mathbb{R}\to \mathbb{R}$，其输入和输出都是标量。如果f的导数存在，这个极限被定义为：

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

如果f’(a)存在，则称f在a处是可微（differentiable）的。如果f在一个区间内的每个数上都是可微的，则此函数在此区间内是可微的。我们也可以把式中的导数f’(x)解释为f(x)相对于x的瞬时（instantaneous）变化率。

定义$u=f(x)=3x^2-4x$，定义函数求解u在x=1处的极限，

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt

def f(x):
    return 3 * x ** 2 - 4 * x

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

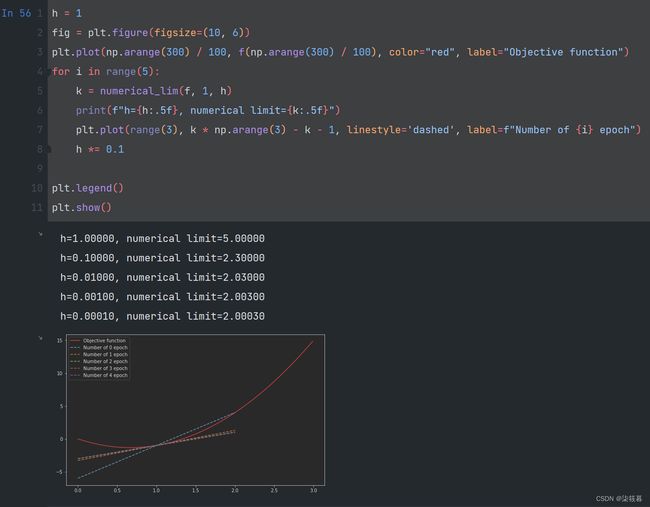
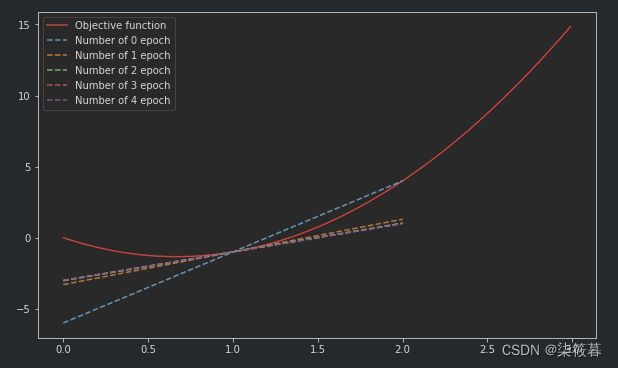
通过令x=1并让h趋近于0，f’(1)的数值结果将趋近于2，图像在5次迭代中得到的斜率所形成的直线逐渐在x=1处与u相切。

h = 1
fig = plt.figure(figsize=(10, 6))
plt.plot(np.arange(300) / 100, f(np.arange(300) / 100), color="red", label="Objective function")
for i in range(5):
    k = numerical_lim(f, 1, h)
    print(f"h={h:.5f}, numerical limit={k:.5f}")
    plt.plot(range(3), k * np.arange(3) - k - 1, linestyle='dashed', label=f"Number of {i} epoch")
    h *= 0.1

plt.legend()
plt.show()

给定y=f(x)，其中x和y分别是函数f的自变量和因变量，在导数的定义中，以下几个表达式是等价的：

$$f^{\prime }(x)=y^{\prime }=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}f}{\mathrm{d}x}=\frac{\mathrm{d}}{\mathrm{d}x}f(x)=Df(x)=D_{x}f(x)$$

其中，符号$\frac{\mathrm{d}}{\mathrm{d}x}$和$D$是微分运算符，表示微分操作。我们可以使用以下规则来对常见函数求微分：

• $DC=0（C是一个常数）$
• $D{x}^n=n{x}^{n-1}（幂律，n是任意实数）$
• $D{e}^x=e^x$
• $D\ln x=\frac{1}{x}$

以下是比较全的导数微分积分基本公式。

假设函数f和g都是可微的，C是一个常数，则其微分遵循以下几个法则：

1. 常数相乘法则
   $$\frac{\mathrm{d}}{\mathrm{d}x}[Cf(x)]=C\frac{\mathrm{d}}{\mathrm{d}x}f(x)$$
2. 加法法则
   $$\frac{\mathrm{d}}{\mathrm{d}x}[f(x)+g(x)]=\frac{\mathrm{d}}{\mathrm{d}x}f(x)+\frac{\mathrm{d}}{\mathrm{d}x}g(x)$$
3. 乘法法则
   $$\frac{\mathrm{d}}{\mathrm{d}x}[f(x)g(x)]=f(x)\frac{\mathrm{d}}{\mathrm{d}x}[g(x)]+g(x)\frac{\mathrm{d}}{\mathrm{d}x}[f(x)]$$
4. 除法法则
   $$\frac{\mathrm{d}}{\mathrm{d}x}[\frac{f(x)}{g(x)}]=\frac{g(x)\frac{\mathrm{d}}{\mathrm{d}x}[f(x)]-f(x)\frac{\mathrm{d}}{\mathrm{d}x}g(x)}{[g(x){]}^2}$$

通过上面的法则，我们可以计算得到函数$u=f(x)=3x^2-4x$的导数$u^{\prime }=f^{\prime }(x)=3\frac{\mathrm{d}}{\mathrm{d}x}{x}^2-4\frac{\mathrm{d}}{\mathrm{d}x}x=6x-4$。令x=1，有u’=2，在之前的绘图中，我们也可以发现当h趋近于0时，所得到的直线的斜率将趋近于2，所以，我们说，当x=1时，此导数也就是曲线$u=f(x)$在x=1处的切线的斜率。

3.2 偏导数

前面我们仅讨论了在只有一个未知变量的情况下对此函数求导，但在一般情况下，函数通常具有多个变量。因此，我们需要将微分的思想推广到多元函数（multivariate function）上。

设$y=f(x_1,x_2,\cdots ,x_n)$是一个具有n个变量的函数。则y关于第i个参数$x_i$的偏导数（partial derivative）为：

$$\frac{\partial y}{\partial x_i}=\underset{h\to 0}{\lim }\frac{f(x_1,\cdots ,x_{i-1},x_i+h,x_{i+1},\cdots ,x_n)-f(x_1,\cdots ,x_i,\cdots ,x_n)}{h}$$

为了计算$\frac{\partial y}{\partial x_i}$，我们通常将除$x_i$以外的其它未知变量看作常数，并计算y关于$x_i$的导数。对于偏导数，以下几个表达式是等价的。

$$\frac{\partial y}{\partial x_i}=\frac{\partial f}{\partial x_i}=f_{x_i}=f_i=D_{i}f=D_{x_i}f$$

根据上面规则，我们可以计算函数$v=f(x,y)=3x^2+2y+1$关于x的偏导为：

$$\frac{\partial v}{\partial x}=\frac{\partial f}{\partial x}=3\frac{\partial }{\partial x}{x}^2=6x$$

3.3 梯度

我们可以把一个多元函数对其所有变量的偏导数连接起来，就得到了该函数的梯度（gradient）向量，其实也就是计算函数在每条轴上的变化率，一条轴对应着一个未知变量的值，求得的斜率构成一个向量就得到了函数梯度。

设函数$f:{\mathbb{R}}^n\to \mathbb{R}$的输入是一个n为向量$x=[x_1,x_2,\cdots ,x_n{]}^T$，输出是一个标量，函数f(x)相对于x的梯度是一个包含n个偏导数的向量：

$${▽}_{x}f(x)=\left[\begin{array}{c}\frac{\partial f(x)}{\partial x_1}\frac{\partial f(x)}{\partial x_2}\cdots \frac{\partial f(x)}{\partial x_n}\end{array}\right]$$

其中，${▽}_{x}f(x)$通常也写成$▽f(x)$。

假设x为n维向量，在对多元函数求微分时经常使用以下规则：

• 对于所有的$A\in {\mathbb{R}}^{m\times n}$，都有${▽}_{x}Ax=A^T$
• 对于所以的$A\in {\mathbb{R}}^{m\times n}$，都有${▽}_x{x}^{T}A=A$
• 对于所以的$A\in {\mathbb{R}}^{m\times n}$，都有${▽}_x{x}^{T}Ax=(A+A^T)x$
• ${▽}_x||x|{|}^2={▽}_x{x}^{T}x=2x$

同样，对于任何矩阵X，都有${▽}_x||x|{|}_F^2=2X$。

下面是一个计算梯度的例子。假设函数$w=f(x,y,z)=3x^3+2y^2+4z$，则该函数在$x,y,z=1,2,3$下的梯度为：

$${▽}_{x}f(x)=\left[\begin{array}{c}\frac{\partial }{\partial x}3x^3\frac{\partial }{\partial y}2y^2\frac{\partial }{\partial z}4z\end{array}\right]=\left[\begin{array}{c}9x^{2}4y4\end{array}\right]=\left[\begin{array}{c}984\end{array}\right]$$

3.4 链式法则

在深度学习中，多元函数通常是复合（composite）的，也就是说有时我们需要对一个函数求导，并将其结果作为另一个函数的参数然后对这另一个函数再求导。链式法则（Chain Rule）可以被用来对复合函数求微分。

在单变量函数复合求导时，假设函数y=f(u)和u=g(x)都是可微的，根据链式法则：

$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\frac{\mathrm{d}u}{\mathrm{d}x}$$

现在考虑一个一般的场景，也就是在多变量函数复合求导时，假设可微函数y有变量$u_1,u_2,\cdots ,u_m$，其中每个可微函数$u_i$都有变量$x_1,x_2,\cdots ,x_n$。注意，y是$x_1,x_2,\cdots ,x_n$的函数。对于任意的$i=1,2,\cdots ,n$，链式法则给出：

$$\frac{\mathrm{d}y}{\mathrm{d}{x}_i}=\frac{\mathrm{d}y}{\mathrm{d}{u}_1}\frac{\mathrm{d}{u}_1}{\mathrm{d}{x}_i}+\frac{\mathrm{d}y}{\mathrm{d}{u}_2}\frac{\mathrm{d}{u}_2}{\mathrm{d}{x}_i}+\cdots +\frac{\mathrm{d}y}{\mathrm{d}{u}_m}\frac{\mathrm{d}{u}_m}{\mathrm{d}{x}_i}$$

3.5 自动微分

深度学习框架通过自动计算导数，即自动微分（automatic differentiation）来加快求导。在实际编码中，系统会根据设计好的模型自动构建一个计算图（computational graph），来跟踪计算是哪些数据通过哪些操作组合起来产生输出。自动微分使得系统能够随后反向传播梯度。这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

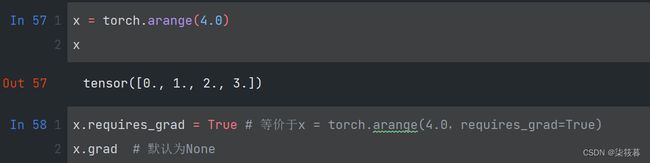
下面是一个自动微分的例子，假设我们想要对函数$y=2x^{T}x$关于列向量x求导，x作为自变量我们可以对其赋予一个初始值。在计算y关于x的梯度之前，需要一个区域来存储梯度，也就是指定requires_grad为True。注意，一个标量函数关于向量x的梯度是向量，并且与x具有相同的形状。

x = torch.arange(4.0)
x

x.requires_grad = True # 等价于x = torch.arange(4.0，requires_grad=True)
x.grad  # 默认为None

现在开始计算y。x是一个长度为4的向量，计算x与x的点积，得到了y的标量输出。接下来，通过调用反向传播函数自动计算得到y关于x的每个分量的梯度，其实也就是x的所有初始值对应在曲线$y=2x^2$上的切线的斜率。函数$y=2x^{T}x$关于x的梯度应为$4x$，我们可以通过逻辑运算快速验证结果是否正确。

y = 2 * torch.dot(x, x)
y

y.backward()  # 调用反向传播
x.grad

x.grad == 4 * x

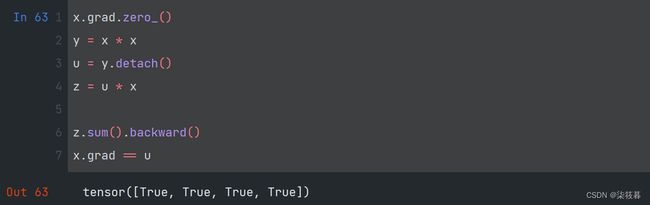
同时在默认情况下，PyTorch会累积梯度，所以我们需要将之前的梯度清零。这样我们需要让x参与其它运算时才不会被上一次遗留的梯度所影响。

x.grad.zero_()  # 梯度清除
y = x.sum()
y.backward()
x.grad

有时，我们需要采用分离计算的方式将某些计算移到记录的计算图之外。例如，假设y是作为x的函数计算的，而z则是作为y和x的函数计算的（如下图a区域所示，其中○代表函数，□代表变量）。我们想计算z关于x的梯度，但由于某种原因，希望将y视为一个常数，并且只考虑x在y被计算后发挥的作用。

a

b

c

y

x

x

z

x

x

x

z

u

x

这里可以分离y来返回一个新变量u（如上图b区域所示），该变量作为一个新的输入变量而不考虑它的内部变量，所以我们在分离计算后对x求偏导，u将会被看作是一个标量（如上图c区域所示），换句话说，梯度不会向后流经u到x。在下面的反向传播函数计算z=u*x关于x的偏导数，同时将u作为常数处理，而不是计算z=x*x*x关于x的偏导数。最后求得的梯度即为常数u。

x.grad.zero_()
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u

由于记录了y的计算结果，因此我们也可以通过调用反向传播函数得到y=x*x关于x的导数，即2x。

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x

四、概率论

4.1 基本概率论

生活中我们掷骰子其实也存在概率问题，如果骰子是公平的，那么所有6个结果{1,2,3,4,5,6}都有相同的可能性发生。因此，我们说1发生的概率为1/6。

对于一个骰子，我们将观察到{1,2,3,4,5,6}中的一个值，对于每个值，我们通常将它出现的次数除以投掷的总次数，叫做此事件（event）概率的估计值。在生活中，常常出现这么一个规律：随着投掷次数的增加，这个估计值会越来越接近真实的潜在概率。数学上我们将它称为大数定律（law of large numbers）。

在统计学中，我们把从概率分布中抽取样本的过程称为抽样（sampling），将概率分配给一些离散选择的分布称为多项分布（multinomial distribution）。借助计算机我们可以通过蒙特卡洛（Monte Carlo）模拟的方法来演示掷骰子问题。

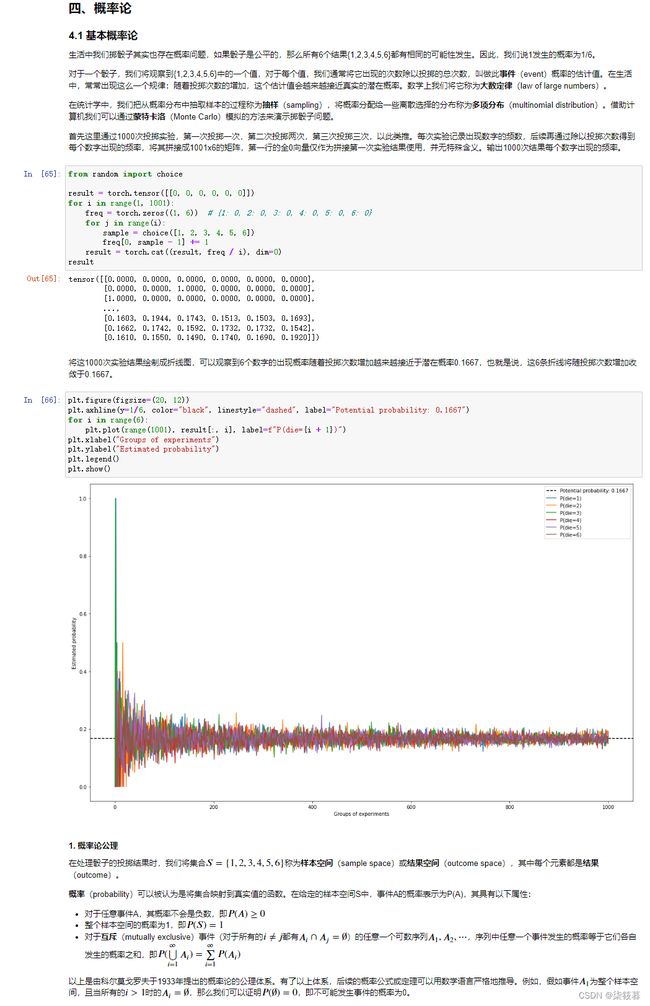
首先这里通过1000次投掷实验，第一次投掷一次，第二次投掷两次，第三次投掷三次，以此类推。每次实验记录出现数字的频数，后续再通过除以投掷次数得到每个数字出现的频率，将其拼接成1001x6的矩阵，第一行的全0向量仅作为拼接第一次实验结果使用，并无特殊含义。输出1000次结果每个数字出现的频率。

from random import choice

result = torch.tensor([[0, 0, 0, 0, 0, 0]])
for i in range(1, 501):
    freq = torch.zeros((1, 6))  # {1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0}
    for j in range(i):
        sample = choice([1, 2, 3, 4, 5, 6])
        freq[0, sample - 1] += 1
    result = torch.cat((result, freq / i), dim=0)
result

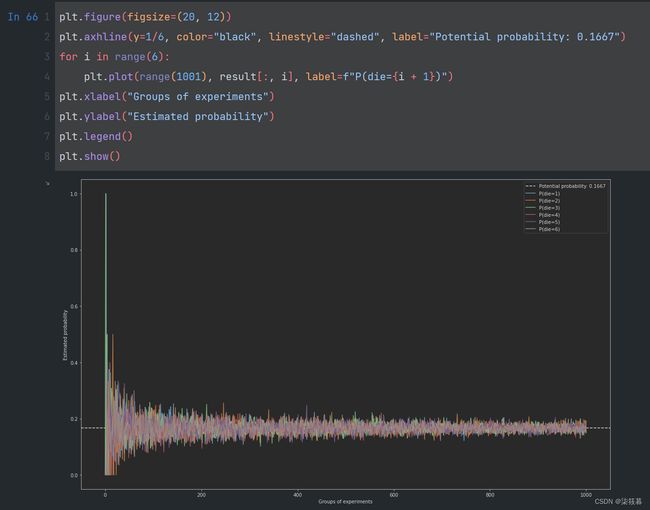
将这1000次实验结果绘制成折线图，可以观察到6个数字的出现概率随着投掷次数增加越来越接近于潜在概率0.1667，也就是说，这6条折线将随投掷次数增加收敛于0.1667。

plt.figure(figsize=(20, 12))
plt.axhline(y=1/6, color="black", linestyle="dashed", label="Potential probability: 0.1667")
for i in range(6):
    plt.plot(range(501), result[:, i], label=f"P(die={i + 1})")
plt.xlabel("Groups of experiments")
plt.ylabel("Estimated probability")
plt.legend()
plt.show()

1. 概率论公理

在处理骰子的投掷结果时，我们将集合$S=\{1,2,3,4,5,6\}$称为样本空间（sample space）或结果空间（outcome space），其中每个元素都是结果（outcome）。

概率（probability）可以被认为是将集合映射到真实值的函数。在给定的样本空间S中，事件A的概率表示为P(A)，其具有以下属性：

• 对于任意事件A，其概率不会是负数，即$P(A)\ge 0$
• 整个样本空间的概率为1，即$P(S)=1$
• 对于互斥（mutually exclusive）事件（对于所有的$i\ne j$都有$A_i\cap A_j=\varnothing$）的任意一个可数序列$A_1,A_2,\cdots$，序列中任意一个事件发生的概率等于它们各自发生的概率之和，即$P(\bigcup _{i=1}^{\infty }{A}_i)=\sum _{i=1}^{\infty }P(A_i)$

以上是由科尔莫戈罗夫于1933年提出的概率论的公理体系。有了以上体系，后续的概率公式或定理可以用数学语言严格地推导。例如，假如事件$A_1$为整个样本空间，且当所有的$i>1$时的$A_i=\varnothing$，那么我们可以证明$P(\varnothing )=0$，即不可能发生事件的概率为0。

2. 随机变量

在我们掷骰子的实验中，我们引入了随机变量（random variable）的概念。考虑一个随机变量X，其值在掷骰子的样本空间$S=\{1,2,3,4,5,6\}$中，我们可以把事件“投到点数为5”表示为{X=5}或X=5，其概率表示为$P(\{X=5\})$或$P(X=5)$。由于概率论中的事件是来自样本空间的一组结果，因此我们可以为随机变量指定值的取值范围，所以我们也可以使用$P(1\le X\le 3)$表示事件$(1\le X\le 3)$，即{X=1,2,3}的概率。

随机变量又分为离散（discrete）随机变量和连续（continuous）随机变量。骰子的每一面可以用离散随机变量表示，而现实生活中的身高和体重则可以用连续随机变量表示。在一些情况下，我们也可以将连续随机变量离散化，例如，把人的身高特征作为一个连续随机变量，当我们限定区间时，比如1.70m~1.79m，它将会被离散化处理。

4.2 多个随机变量

在很多时候，我们需要考虑多个随机变量。例如，在对做出房价预测时，我们需要考虑到影响房价的所有因素，就比如房屋面积或者楼层数，它们都可以是一个影响房价的随机变量。

1. 联合概率

我们把影响房价的因素之一房屋面积记为随机变量A，把影响房价的另一个因素楼层数记为随机变量B，那么它们的联合概率（joint probability）为$P(A=a,B=b)$，也可简单记为$P(AB)$。给定任意值a,b，联合概率可以解释为当A=a与B=b同时满足的概率是多少？同时因为需要满足的条件有两个，所以子事件发生的概率通常要大于两个事件同时发生的概率，并且所以子事件发生的概率的乘积即为事件A=a与B=b同时满足发生的概率（假设A，B相互独立）。即下面式子也将成立：

• $P(A)\ge P(AB)$且$P(B)\ge P(AB)$
• 当A，B相互独立时，$P(A)\times P(B)=P(AB)$

2. 条件概率

通过上面联合概率的不等式我们可以得到一个比率：$0\le \frac{P(A=a,B=b)}{P(A=a)}\le 1$。我们称这个比率为条件概率（conditional probability），并用$P(B=b|A=a)$或$P(B|A)$表示：它是事件B=b在事件A=a已发生的前提下发生的概率。记为：

$$P(B|A)=\frac{P(AB)}{P(A)}$$

3. 贝叶斯定理

使用条件概率的定义，我们可以得到统计学中有名的方程之一：贝叶斯定理（Bayes theorem）。根据乘法法则（multiplication rule）可得到$P(AB)=P(B|A)P(A)$。根据对称性，又可得到$P(AB)=P(A|B)P(B)$。假设$P(B)>0$，求解其中一个条件变量，我们得到：

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

其中P(A,B)是一个联合分布（joint distribution），P(A|B)是一个条件分布（conditional distribution），这种分布可以在给定值A=a，B=b上进行求值。

4. 边际化

为了进行事件概率求和，我们需要求和法则（sum rule），即B的概率相当于计算A的所有可能的选择，并将所有选择的联合概率聚合在一起：

$$P(B)=\sum _{A}P(AB)$$

这被称之为边际化（marginalization），边际化结果的概率或分布称为边际概率（marginal probability）或边际分布（marginal distribution）。

5. 独立性

依赖（dependence）和独立（independence）也是有用的属性。如果两个随机变量A和B是独立的，意味着事件A的发生跟事件B的发生无关，因为两个事件的发生互不影响，所以$P(A|B)$也可以直接写成$P(A)$。比如，连续投掷一个骰子，其每次投掷的结果都是相互独立的。相比之下，灯开关的位置和房间的亮度并不是相互独立的。

由于$P(A|B)=\frac{P(AB)}{P(B)}=P(A)$等价于$P(AB)=P(A)P(B)$（也就是联合概率的第二个式子），因此两个随机变量是独立的，当且仅当两个随机变量的联合分布是其各自分布的乘积。同样的，给定另一个随机变量C时，两个随机变量A和B是条件独立的（conditionally independent），当且仅当$P(A,B|C)=P(A|C)P(B|C)$。这个情况表示为$A\perp B|C$。

4.3 期望与方差

为了概括概率分布的关键特征，我们需要一些测量方法。一个随机变量X的期望（expectation）或平均值（average）表示为：

$$E(X)=\sum _{x}xP(X=x)$$

当函数f(x)的输入是从分布P中抽取的随机变量时，f(x)的期望为：

$$E_{x-P}[f(x)]=\sum _{x}f(x)P(x)$$

在许多情况下，我们希望衡量随机变量X与其期望的偏差。可以通过方差来量化：

$$Var(X)=E(X-E(X{)}^2)=E(X^2)-E(X{)}^2$$

方差的平方根被称为标准差（standard deviation）。随机变量函数的方差衡量的是，当从该随机变量分布中抽取不同值x时，函数值偏离该函数的期望的程度：

$$Var[f(x)]=E((f(x)-E(f(x)){)}^2)$$

边际分布*（marginal distribution）。

5. 独立性

依赖（dependence）和独立（independence）也是有用的属性。如果两个随机变量A和B是独立的，意味着事件A的发生跟事件B的发生无关，因为两个事件的发生互不影响，所以$P(A|B)$也可以直接写成$P(A)$。比如，连续投掷一个骰子，其每次投掷的结果都是相互独立的。相比之下，灯开关的位置和房间的亮度并不是相互独立的。

由于$P(A|B)=\frac{P(AB)}{P(B)}=P(A)$等价于$P(AB)=P(A)P(B)$（也就是联合概率的第二个式子），因此两个随机变量是独立的，当且仅当两个随机变量的联合分布是其各自分布的乘积。同样的，给定另一个随机变量C时，两个随机变量A和B是条件独立的（conditionally independent），当且仅当$P(A,B|C)=P(A|C)P(B|C)$。这个情况表示为$A\perp B|C$。

4.3 期望与方差

为了概括概率分布的关键特征，我们需要一些测量方法。一个随机变量X的期望（expectation）或平均值（average）表示为：

$$E(X)=\sum _{x}xP(X=x)$$

当函数f(x)的输入是从分布P中抽取的随机变量时，f(x)的期望为：

$$E_{x-P}[f(x)]=\sum _{x}f(x)P(x)$$

在许多情况下，我们希望衡量随机变量X与其期望的偏差。可以通过方差来量化：

$$Var(X)=E(X-E(X{)}^2)=E(X^2)-E(X{)}^2$$

方差的平方根被称为标准差（standard deviation）。随机变量函数的方差衡量的是，当从该随机变量分布中抽取不同值x时，函数值偏离该函数的期望的程度：

$$Var[f(x)]=E((f(x)-E(f(x)){)}^2)$$