Dijkstra算法以及它的堆优化

.Dijkstra算法用来干什么的？
. 生活中常常会遇到从一个点到另一个点有很多条路，但要选择一条最短的路。类似这样的求一个点到另一个点最短路劲的单源最短路径问题（都是正权），而Dijkstra就是解决这个问题的算法
.时间复杂度
数组实现 O( n² ）
二叉堆 O( ( V + E )lg V)
斐波那契堆 O( E + Vlg V ) —>实际意义不大知道就行
一.普通Dijkstra算法思路
1. Dijkstra算法采用的是一种贪心的策略，声明一个dis的数组来保存源点到其他点的最短路径长度，最开始都设为无穷大，以及一个已经找到最短路径的顶点的集合T。
2. 初始时我们将源点s到源点的路径长度置0，dis[s] = 0,将源点放进集合T中。找到源点所能到达的点（v,w） (v是源点能到的点，w是源点到v点的路长)令dis[v] = w。
3. 接下来从未在集合中的点的dis数值中选出最小的，将这个点加入到集合T中。
4. 接下来要进行判断新加入的结点所能到达的点的路径长度是否小于dis数组中的数值，如果小于，则将dis进行数值更新。
5. 重复3，4操作，直到T中包含了所有点。
二.普通Dijkstra算法代码实现

#include              //Dijkstra算法模板（邻接矩阵）
#include 

#define N 105
#define INF 9999

using namespace std;

int road[N][N];
int dis[N],vis[N];
int n,m,h;
int s;
int u,v,w;

void Dijkstra(int x)
{
    for(int i = 1; i <= n; i++)
    {
        dis[i] = road[x][i];
    }

    dis[x] = 0;
    vis[x] = 1;


    int next = 0;

    for(int i = 1; i <= n; i++)
    {
        int l = 1e10 + 10;

        for(int j = 1; j <= n; j++)
        {
            if(vis[j] == 0 && l > dis[j])
            {
                l = dis[j];
                next = j;

            }
        }

        vis[next] = 1;

        for(int j = 1; j <= n; j++)
        {
            if(vis[j] == 0 && dis[j] > road[next][j] + dis[next])
            {
                dis[j] = road[next][j] + dis[next];
            }
        }
    }
}

int main()
{
    while(~scanf("%d%d",&n,&m))              //这里输入有多少个城市,有多少条路
    {
        printf("请输入起始点：");
        scanf("%d",&s);                 //这里输入起始点（求的就是从这个点到其它点的最短路）

        memset(road,INF,sizeof(road));     //将点与点之间路的长度初始话为∞
        memset(dis,0,sizeof(dis));          
        memset(vis,0,sizeof(vis));
        h = road[1][1];

        for(int i = 1; i <= m; i++)
        {
            scanf("%d%d%d",&u,&v,&w);       //这里输入路的信息（两个点与它们路的长度）

            road[u][v] = road[v][u] = w;        //我这里写的是无向图
        }

        Dijkstra(s);

        for(int i = 1; i <= n; i++)
        {
            if(i == s)
            {
                continue;
            }

            if(dis[i] == h)
            {
                printf("点%d到点%d没有路\n",s,i);
                continue;
            }

            printf("点%d到点%d的最短路径为%d\n",s,i,dis[i]);
        }
    }
}

从普通的Dijkstra算法中我们可以看到有找到最小边这个步骤，那么我们可以运用优先队列来缩短这个过程。
二.Dijlstra的二叉堆优化
.思路图示

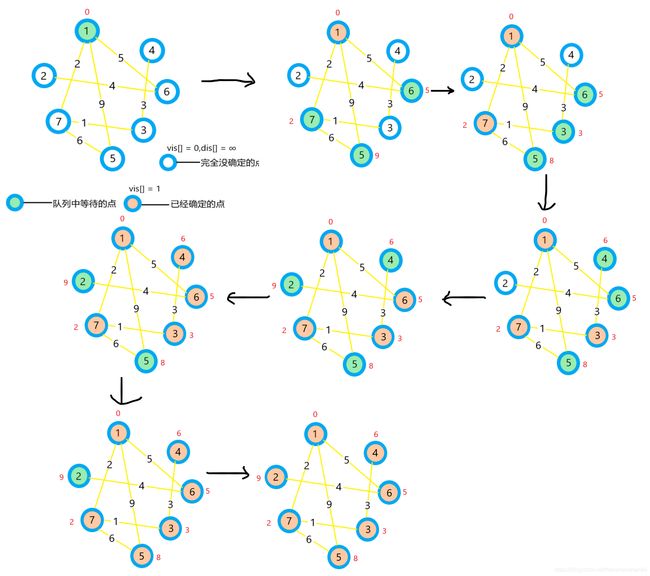
算法实现
邻接矩阵实现：

#include              //Dijkstra二叉堆优化算法模板（邻接矩阵）
#include 
#include 

#define N 105
#define INF 9999

using namespace std;

int road[N][N];
int dis[N];
int n,m;
int s;
int u,v,w;

struct Node
{
    int ss,ww;

    bool operator < (const Node &t) const
    {
        return t.ww < ww;
    }
};

void Dijkstra(int x)
{
    priority_queue<Node> p;

    dis[x] = 0;
    p.push({x,0});

    while(!p.empty())
    {
        Node q = p.top();
        p.pop();
        if(dis[q.ss] < q.ww)
        {
            continue;
        }

        for(int i = 1; i <= n; i++)
        {
            if(dis[i] > road[q.ss][i] + q.ww)     //dis数组数值更新（核心思想）
            {
                dis[i] = road[q.ss][i] + q.ww;
                p.push({i,dis[i]});    //将周围点与它们更新后的dis数值入队
            }
        }
    }

}

int main()
{
    while(~scanf("%d%d",&n,&m))              //这里输入有多少个城市,有多少条路
    {
        scanf("%d",&s);                 //这里输入起始点（求的就是从这个点到其它点的最短路）

        memset(road,INF,sizeof(road));     //将点与点之间路的长度初始话为∞
        for(int i = 1; i <= n; i++)       //将初始点到其他点的最短路初始化为∞
        {
            dis[i] = INF;
        }

        for(int i = 1; i <= m; i++)
        {
            scanf("%d%d%d",&u,&v,&w);       //这里输入路的信息（两个点与它们路的长度）

            road[u][v] = road[v][u] = w;        //我这里写的是无向图
        }

        Dijkstra(s);

        for(int i = 1; i <= n; i++)
        {
            if(i == s)
            {
                continue;
            }

            if(dis[i] == INF)
            {
                printf("点%d到点%d没有路\n",s,i);
                continue;
            }

            printf("点%d到点%d的最短路径为%d\n",s,i,dis[i]);
        }
    }
}

邻接表实现，因为基本上问题都是稀疏图，所以推荐用这个。

#include          //Dijkstra二叉堆优化算法模板（邻接表）
#include 
#include 

#define N 105
#define INF 9999

using namespace std;

int h[N*N],tot;
int dis[N];
int n,m;
int s;
int u,v,w;

struct Node
{
    int to,w,next;
}node[N*N];

struct Node2
{
    int ss,ww;

    bool operator < (const Node2 &t) const
    {
        return t.ww < ww;
    }
};

void add(int u,int v,int w)
{
    node[tot].to = v;
    node[tot].w = w;
    node[tot].next = h[u];
    h[u] = tot++;
}

void Dijkstra(int x)
{
    priority_queue<Node2> p;

    dis[x] = 0;
    p.push({x,0});

    while(!p.empty())
    {
        Node2 q = p.top();
        p.pop();

        if(dis[q.ss] < q.ww)
        {
            continue;
        }

        for(int i = h[q.ss]; i != -1; i = node[i].next)
        {
            int to = node[i].to;

            if(!vis[to] && dis[to] > node[i].w + q.ww)     //dis数组数值更新
            {
                dis[to] = node[i].w + q.ww;
                p.push({to,dis[to]});
            }
        }
    }
}

int main()
{
    while(~scanf("%d%d",&n,&m))              //这里输入有多少个城市,有多少条路
    {
        printf("输入起始点:");
        scanf("%d",&s);                 //这里输入起始点（求的就是从这个点到其它点的最短路）

        memset(h,-1,sizeof(h));
        tot = 1;

        for(int i = 1; i <= n; i++)       //将初始点到其他点的最短路初始化为∞
        {
            dis[i] = INF;
        }

        for(int i = 1; i <= m; i++)
        {
            scanf("%d%d%d",&u,&v,&w);       //这里输入路的信息（两个点与它们路的长度）

            add(u,v,w);        //我这里写的是无向图
            add(v,u,w);
        }

        Dijkstra(s);

        for(int i = 1; i <= n; i++)
        {
            if(i == s)
            {
                continue;
            }

            if(dis[i] == INF)
            {
                printf("点%d到点%d没有路\n",s,i);
                continue;
            }

            printf("点%d到点%d的最短路径为%d\n",s,i,dis[i]);
        }
    }
}