【读书笔记——开关电源】《精通开关电源设计》(1)
第一章 开关功率变换原理
文章目录
- 第一章 开关功率变换原理
-
- 前言
- 1.1 概念和基本术语
- 1.2 电感
-
- 电感充放电的基本原理
- 功率变化中的稳态与不同工作模式
- 伏秒定律与占空比
- 开关器件的使用与保护
- 1.3 开关拓扑的演变
-
- 通过二极管控制感应电压的尖峰
- 三种基本拓扑
-
- 升降压变化器
- 升压拓扑
- 降压拓扑
- 结语
前言
近期需要使用开关电源,阅读了一些资料,还是想打稳整个基础,故而在阅读《精通开关电源设计》一书时完成了如下笔记。计划在后续逐步更新,完成该书部分章节的阅读,也会结合一些其他资料辅助理解。我还计划完成一些开关电源的设计、绘制和实际调试工作,届时也会一并更新。
本人刚刚接触相关内容,第一次写博客,文章中一定免不了错误与纰漏,还请大家多多指出。
1.1 概念和基本术语
本段主要介绍基本概念及术语从书中1.1及1.2中提取,若已知或直接读起来较为疑惑可跳过不看,直接进入本文下一节。为方便查找,将本段提到的术语罗列如下——
DC-DC变换器、工况、电网调整、负载调整、环路响应(=交流响应)、功率损耗、线型调整器、低压降调整器(LDO)、MOSFET、BJT、寄生参数、DCR、ESR、ESL、开关损耗(=交叉损耗)、热管理、应力降频
-
DC-DC 变换器是现代高频开关电源的基本组成部分。顾名思义,它把直流(DC) 输人电压VIN 变换成更满足要求的或更有效的直流输出电压VO。
-
给定输出电压下的两种工况:
Vin在工作范围内变化时,保持输出电压稳定的过程——电网调整;Io在工作范围内变化时(轻载到重载),保持输出电压稳定的过程称为负载调整。 -
环路响应:
电源(在电网电压或负载突变时)的输出调整速率也很重要,变换器在外部扰动下的即速调整(校正)性能称为环路响应或交流响应。 -
功率损耗:
输入功率PIN;输出功率PO;功率损耗 P l o s s = P I N − P O P_{loss}=P_{IN}-P_{O} Ploss=PIN−PO,也可以用效率 η \eta η来表示。可以推得:
P l o s s = V I N ∗ ( I I N _ m e a s u r e − I I N _ i d e a l ) P_{loss}=V_{IN}*(I_{IN\_measure}-I_{IN\_ideal}) Ploss=VIN∗(IIN_measure−IIN_ideal) -
线性调整器:
相当于在电路中串联了可变电阻,该可变电阻对电路进行分压。当然在实际电路中,这个可变电阻为一个工作在可变电阻区(线性区)的三极管。- 有最小压差的限制,往往不能完成大压降,同时也仅仅能够降压。输入勉强高于输出就能工作的调整期叫做低压降调整器(LDO)。
- 该调整器效率不高,相比于开关器件。后者工作在开关状态,通过储能完成DC-DC转换,理想效率为100%。
- 较为安静,没有噪声问题
-
半导体开关器件(MOSFET与BJT的对比):
- 驱动MOSFET采用栅极电压,是压控型器件;BJT需要较大的基极电流注入才行。
- BJT的噪声、电磁干扰、纹波要比MOSFET有优势
-
电抗元件的储能:
电容存储静电能;电感存储磁能
W C = C V 2 2 ; W L = L I 2 2 W_C=\frac{CV^2}{2}; W_L=\frac{LI^2}{2} WC=2CV2;WL=2LI2 -
寄生参数的影响:
以下这些使得开关电源效率无法100%,但其存在也可以提高稳定性。
DCR——电感除了具有基本电感特性外,还具有一定的非零直流电阻
ESR——电容除了具有基本电容特性外,还具有阻值很小的等效串联电阻
ESL——电容引线、金属销及端子存在小电感,所以电容具有等效串联电感
-
高频开关的优劣
降低开关频率有利于提高效率,要尽可能选择在人类听觉频率(20Hz-2kHz)范围外的开关频率;提升开关频率可以减小元件尺寸,同时还可以增强环路响应(发生外部扰动时快速纠正的能力)。
综上:结合前文所述,提高开关频率的唯一阻碍就是开关损耗(也称交叉损耗)。
-
可靠性、使用寿命、热管理及应力降频
热管理——尽可能把电源产生的热量散发到周围环境中去,从而降低电源内部各工作元器件自身的温度。
失效率随时间的变化,有一条著名的经验法则—一温度每升高10℃ ,失效率加倍。
温度最终可看作热应力(物体因热力形变,而导致的物体内部之间的相互作用力),是失效率增加的原因之一。应力降额是优秀的设计人员用来降低元器件内部应力及其失效率的一种常用技术。
1.2 电感
本节中虽然标题为电感,但书中对该部分做了较多引申,本节是理解开关电源的关键一节,需要着重阅读。
电感充放电的基本原理
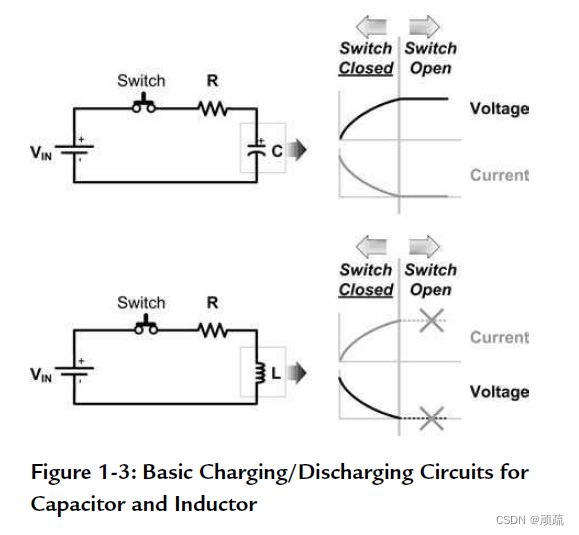
电容与电压的关系直接,有无数动画解释了两者的关系。我们通常会使用对偶定理来通过电容理解电感,但往往对该定理理解不足,导致错误使用该定理。为正确使用对偶定理,在讨论电感前,我们需要先对电容的充放电有所理解,如下图所示:
电容的电压与电流曲线都可以通过求解微分方程解得,链接中给出了详细推导,可以注意一下时间常数 τ \tau τ。开关打开后,电流被强迫为0,而电容电压则会保持原来状态。如果以此猜测对偶的曲线(如上图),那必定是错误的。真正的对偶电路应该如下图。
注:对偶原理涉及的拓扑变换有:电容和电感互换、电阻和电导互换、电流源和电压源互换。
接下来,我们尝试更加深入的理解电感,由上图可知,电感在电压源作用下进行充电,其电流不断增加,此时电感两端居然是存在电压的(但电感几乎没有电阻)?电感可以保持电压的原因是楞次定律和法拉第定律。
注:感应电流的磁通必须反抗引起它的磁通变化,感应电流具有的以及消耗的能量,必须从引起磁通变化的外界获取。
电感的感应电压可以与电容的位移电流进行类比,如上图,当电感放电迅速时(但不能突变),会产生一个极高的电压(产生电弧)。在研究电感时,由于其电压完全由电流决定,因此应该始终注意电感电流的表现。
要注意的是,在切断电流时,电感电压反向,此时可以将电感看作一个电压源(以试图保持原来的流向状态,保证电流连续), 可参考下图理解。
功率变化中的稳态与不同工作模式
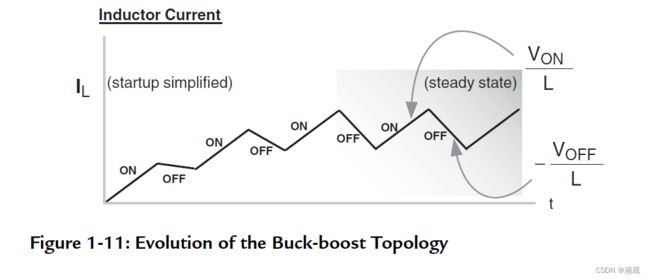
开关周期结束时,电感的状态很容易不稳定,即电流不回到周期开始时的初值。如若这样,在后续的开关中,该电流增量就会不断累加,使得电路持续变化。可知,如若想要达到稳态,就需要满足开关导通阶段的电流增量( Δ \Delta ΔION)等于关断阶段电流减量( Δ \Delta ΔIOFF),也即 Δ \Delta ΔION= Δ \Delta ΔIOFF。
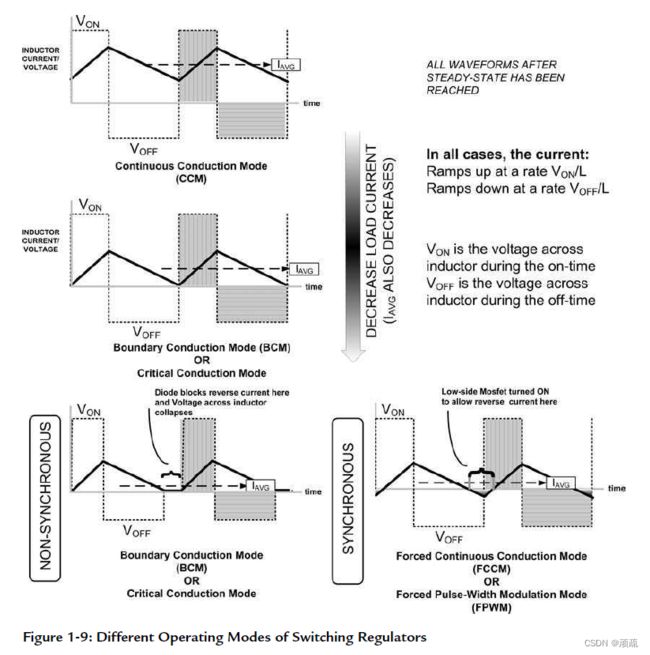
要注意的是,这里我们关心的只是增量,但并不关心每个阶段的电流绝对值是多少。事实上,每个开关周期电流都恢复到0的称为断续导通模式(DCM),而稳态电流无论如何变化,其值总大于0的称为连续导通模式(CCM),后者较为常见,如果正好为0则为临界导通模式(BCM),具体可见下图,图中的FCCM与FPWM采用的是栅极管而非二极管(即同步拓扑,后文中会提到),所以有负半轴的部分。
伏秒定律与占空比
伏秒定律——导通阶段的电感电压与其作用时间(即导通时间)的乘积必然等于关断阶段的电感电压与其作用时间的乘积。
V O N × t O N = V O F F × t O F F V_{ON} \times t_{ON}=V_{OFF} \times t_{OFF} VON×tON=VOFF×tOFF
该乘积称为伏秒积 E t Et Et,如果用电压曲线进行描述,可以视为导通与关断期间两个面积相等。实际应用中,由于尺度考虑,多使用伏微秒积。
占空比的定义是开关的导通时间与开关周期之比。也即:
D = t O N T D=\frac{t_{ON}}{T} D=TtON
若为连续导通模式,可以进一步有:
D = t O N t O N + t O F F D=\frac{t_{ON}}{t_{ON}+t_{OFF}} D=tON+tOFFtON
开关器件的使用与保护
为了防止开关器件(或变换器)过流,需要设置限流保护。这种情况下,将检测电感电流或开关器件电流,然后与设定的阙值相比较。如果在开关器件导通的某一瞬间过流,控制电路将迫使开关器件立刻关断直至周期结束,以求自保。
但下一周期不会记住前一周期所发生的任何事
件。因此,每一个开关周期都要重新连续检测电流,确保电流在安全范围内。不然的话,保护动作将重新开始。而且如果有必要,其后若干个周期内保护动作将重复进行,直至过流消失。
1.3 开关拓扑的演变
通过二极管控制感应电压的尖峰
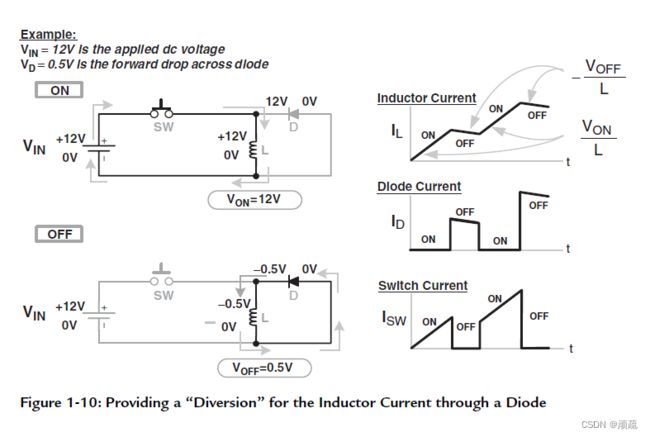
参考“电感充放电的基本原理”一节,我们需要解决——设法把感应电压控制在有限的水平。前文书说道,感应电压的产生仅仅与电流相关,故而需要给电流找到去处,有意识的提供续流回路。下图中给出了续流回路,该回路由二极管构成。
开关闭合时,走电源这个回路;断开时,如图可见,感应电压迫使二极管导通。在这样操作后,不可控的电压尖峰消除了,但电流的阶梯式上升并未解决。
解决阶梯式电流的方法是让电感完成复位,可以在二极管处放置电容,如下图。二极管电流向电容充电,电感上的压降此时比上图大,电流变化率也就更大,从而能够达到平衡。
三种基本拓扑
下图中给出了三种基本的拓扑,在所有拓扑中,电感的一端需连接到三个可用的直流端(输人、输出或地)之一。电感另一端的电压持续跳变,因此称为开关结点(SW点)。在设计电路板时,交换节点处不要铺设太多的铜,否则会形成有效的电场天线,向四周喷射放射状的射频干扰。
升降压变化器
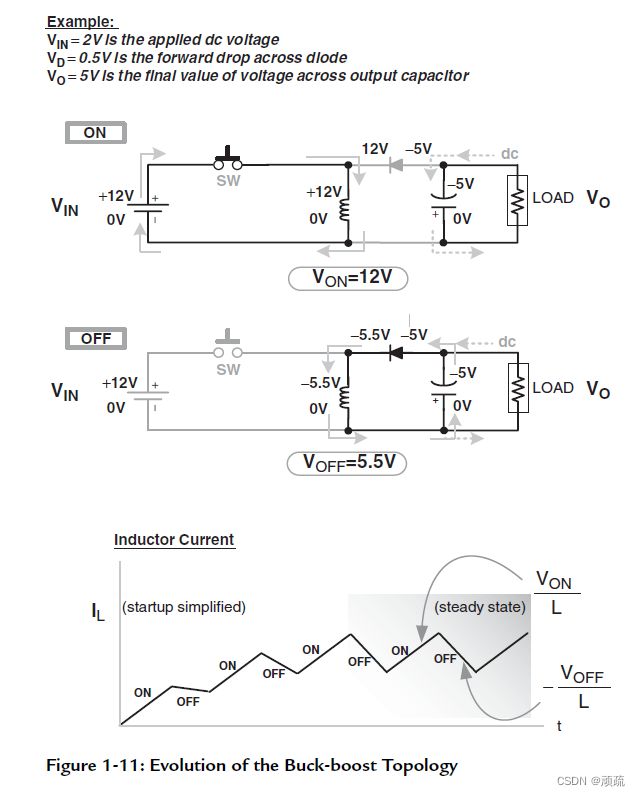
对于每个周期内,电流的上升阶段的斜率是不变的,等于 V I N / L V_{IN}/L VIN/L(原因是 V = L d I / d t V=LdI/dt V=LdI/dt)。下降段的初始斜率为 V D / L V_{D}/L VD/L,其中 V D V_{D} VD是二极管的压降,此时 Δ I O N > Δ I O F F \Delta I_{ON}>\Delta I_{OFF} ΔION>ΔIOFF,因此电流开始阶梯上升。但是当电源充电后,电流下降的斜率变得越来越大。最终达到稳态。
要注意的是,这种Buck-Boost电路的输出与输入是反向的,因此升降压变换器经常被称为反超性拓扑。
如下图所示,该拓扑的平均输入电流等于平均开关电流;平均输出电流等于平均二极管电流。这里可以结合电路图进行理解,根据节点电流法,电感电流 I L I_L IL等于在不同时间段开关与二极管电流的叠加。
对上述内容进行总结如下:
- 开关导通时,能量从输入直流电源通过开关传输给电感,没有能量传输给输出端。
- 开关断开时,电感储能通过二极管传输到输出端,没有直接来自输入直流电源的能量。
- 升降压拓扑是唯一的纯反激拓扑,所有从输入传输到输出传输的能量必须先存储在电感中。
- 发热量与电流有效值(RMS) 的平方成正比。由千斩波式波形的有效值较大,升降压变换器的效率并不是很高。而且,电路板上的噪声和纹波通常也比较大。因此,可能需要在升降压变换器的输人端外加滤波器,输出端通常也是如此。
- 虽然输出电容在开关关断时充电,在开关导通时为负载供电,但平均电容电流始终为零。事实上,根据定义,稳态时的平均电容电流必须为零,否则电容或充或放,直至达到稳态,就像电感电流一样。既然输出电容的平均电流为零,那么升降压变换器的平均二极管电流必然等于负载电流(否则电流从哪里来呢)。
平均电感电流 I L I_L IL、负载电流 I O I_O IO、二极管平均电流与电感电流额定值(其中1.2是系数,符合一般设计规则):
I D _ A V G = I O = I L × ( 1 − D ) I_{D\_AVG}=I_O=I_L\times(1-D) ID_AVG=IO=IL×(1−D)
额定电流值: 1.2 × I L = 1.2 × I O 1 − D 额定电流值:1.2\times I_L = 1.2\times\frac{I_O}{1-D} 额定电流值:1.2×IL=1.2×1−DIO
升压拓扑
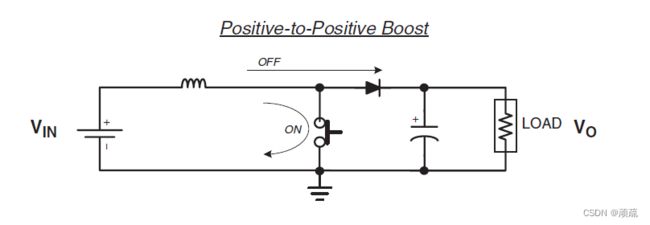
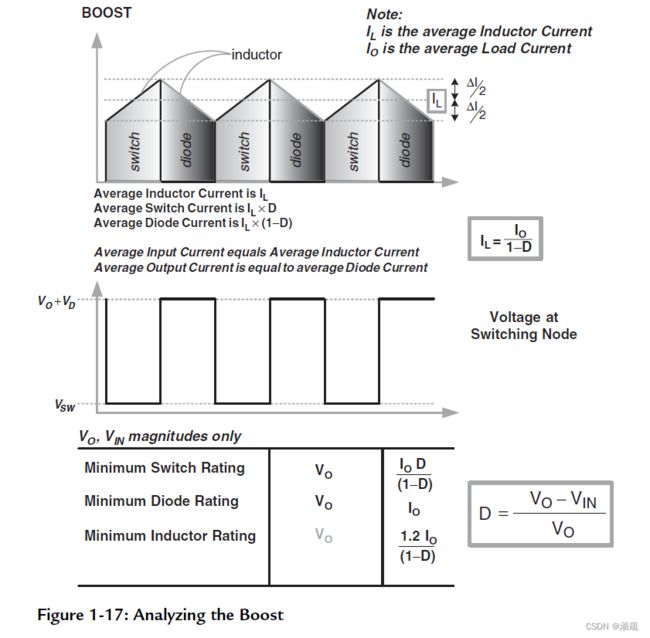
在了解了升降压电路的原理后,其余两种拓扑就比较容易理解了。下图中是一个Boost电路,可以对其进行分析如下:
- 开关关断时,电感储能(通过二极管)传输到输出。但是,输出中有一部分能量直接来自输入直流电源。
- 输入电容(直流源)电流是“平滑”的,因为输入电容与电感串联(电感可防止电流跳变)。
- 但输出电容电流是斩波式的,因为它与稳定的负载电流( I O U T I_{OUT} IOUT) 叠加构成二极管电流(它在所有拓扑中都是斩波式的)。
降压拓扑
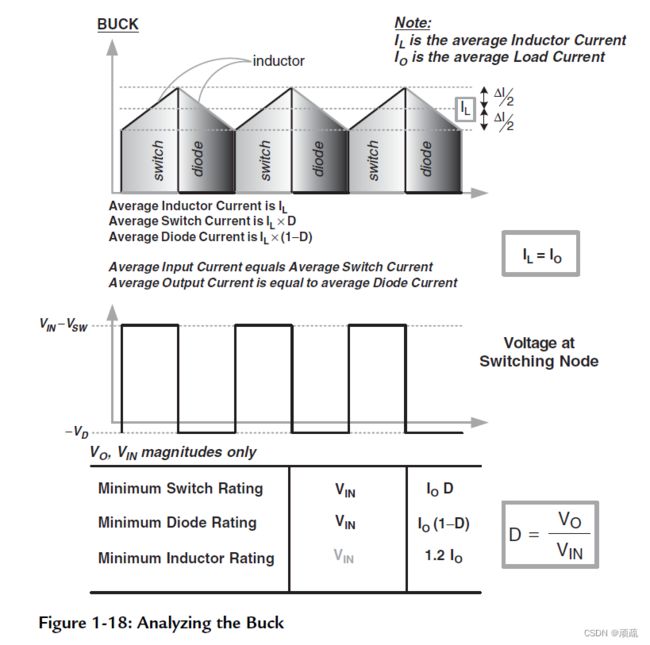
如下图,对降压拓扑做如下分析:
- 开关导通时,能量从输入直流电源(通过开关)传输给电感,同时有一部分能量直接传递到输出端。
- 开关关断时,电感储能(通过二极管)传输到输出,没有能量来自输人直流电源。
- 输入电容(直流源)电流是斩波式的。该电流与直流电源输出的稳定的直流( I I N I_{IN} IIN) 叠加构成开关电流(它在所有拓扑中都是斩波式的)。
- 但是,输出电容电流是“平滑"的,因为输出电容与电感串联(电感可防止电流跳变)。
- 既然输出电容的平均电流为零,那么降压变换器的平均电感电流必然等于负载电流(否则电流从哪里来呢)。
结语
至此。第一章的读书笔记撰写完成。这个写东西的流程还没跑熟,markdown插图片整的有点麻烦,下次搞个图床应该会好些,本地的md复制上来就能直接使用了。