代码随想录算法训练营Day9 | 28. 找出字符串中第一个匹配项的下标 | 459. 重复的子字符串
文章目录
- KMP 算法
-
- KMP:字符串匹配
- 相关定义
- 前缀表(prefix table)
- 前缀表与 next 数组
- 复杂度分析
- 构造 next 数组
-
- 初始化
- 前后缀不相同
- 前后缀相同
- 整体代码
- 28. 找出字符串中第一个匹配项的下标
- 459. 重复的子字符串
-
- 暴力解法
- 移动匹配
- KMP 应用
- 思路
KMP 算法
理论与实现 | 理论视频 | 实现视频
主要思想:当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。
KMP:字符串匹配
给定输入:文本串、模式串,判断模式串是否在文本串中出现。
例如:文本串 aabaabaafa
\hspace{5.5ex} 模式串 aabaaf
暴力算法的思路是,对文本串中的每个索引,如果匹配出现冲突,则模式串回到起点,文本串移到下一个索引开始匹配。
KMP 算法的优势是,当出现冲突的时候,不必从模式串的起点重新开始,也不必从文本串的下一个索引开始。
相关定义
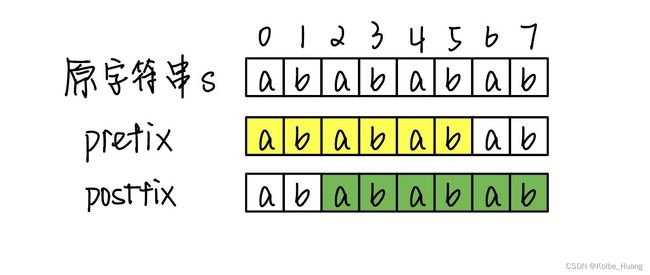
- 前缀:所有以第一个字符开头、不包含最后一个字符的连续子串。
- i.e.,
s[:i]where 0 ≤ i < n 0\leq i < n 0≤i<n
- i.e.,
- 后缀:所有以最后一个字符结尾、不包含第一个字符的连续子串
- i.e.,
s[i:]where 0 < i < n 0 < i < n 0<i<n
- i.e.,
- 前缀表:记录模式串中每个从头开始的子串的最长相同前后缀的长度
例如模式串 aabaaf 中的子串 aabaa,最长相同前后缀的长度是2,因为长度为3的前缀为 aab,长度为3的后缀为 baa,并不相同。
而子串 a 的最长相同前后缀的长度是0(不存在前后缀)。
前缀和后缀都是从左往右定义的,后缀不是从右往左定义!
前缀表(prefix table)
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 模式串 | a | a | b | a | a | f |
| 前缀表 | 0 | 1 | 0 | 1 | 2 | 0 |
在之前的例子中,当匹配到模式串的 f 时,出现了冲突,此时根据前缀表我们可以找到下标为 2 的元素,也就是 b,然后继续开始模式串的匹配(文本串中的指针从 index=6 开始移动,模式串中的指针从 index=2 开始移动)。
其中的思想是,在 f 之前的子串 aabaa 中,最长相同前后缀的长度为2(aa)。因此,冲突的字符 f 出现在最长后缀 aa 的后面,所以我们跳转到对应的最长前缀 aa 的后面,也就是下标为2的位置。此时,由于已知长度为2的前后缀相同,我们知道发生冲突的字符 f 前面肯定已经出现过 aa,所以模式串的匹配可以接着直接从最长前缀的后面(下标为2的位置)开始。
前缀表含义:令模式串为s,对于下标 i ,prefix[i] 代表了模式串中下标 i 之前(包括 i),即s[:i+1]中,的最大相同前后缀的长度。
前缀表与 next 数组
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 模式串 | a | a | b | a | a | f |
| 前缀表 | 0 | 1 | 0 | 1 | 2 | 0 |
| next 数组 1 | -1 | 0 | 1 | 0 | 1 | 2 |
| next 数组 2 | -1 | 0 | -1 | 0 | 1 | -1 |
可以看到,前缀表的写法是以上描述的思路,而 next 数组则略有不同。这样的不同主要是代码实现上的区别,含义没有发生大的变化:
- next 数组1 的写法代表着对于下标
i,代表了s[:i]中的最大相同前后缀的长度。 - next 数组2 的写法是前缀表中所有元素都减一。
复杂度分析
令文本串的长度为 n,模式串的长度为 m。
在匹配过程中,文本串的指针仅会遍历一次,时间复杂度为 O ( n ) O(n) O(n);同时需要遍历一次模式串生成 next 数组,时间复杂度为 O ( m ) O(m) O(m)。总的时间复杂度为 O ( m + n ) O(m+n) O(m+n),远超暴力算法的复杂度 O ( m n ) O(mn) O(mn)。
构造 next 数组
next[i] 代表了模式串中下标 i 之前(包括 i),即s[:i+1]中,的最大相同前后缀的长度。
我选择的方法是构造和前缀表完全相同的 next 数组。
- 初始化
- 处理前后缀不相同的情况
- 处理前后缀相同的情况
定义两个指针:
i:当前的子串尾(包括下标 i),个人希望命名为substring_end- 同时也代表着后缀的尾部
- 当前考虑的是子串
s[:i+1]
j:最大相同前后缀的长度,个人希望命名为max_equal_len- 同时也代表着最大相同前缀的尾部(不包括下标 j)
构造思路类似于 dynamic programming,充分利用已经计算过的情况。
初始化
根据定义,刚开始的时候考虑的子串仅包括模式串的第一个元素,此时最大相同前后缀的长度为0。
next[0] = 0 # string with one element has no prefix and postfix
j = 0 # current max equal prefix and postfix has length 0
i = 1 # no need to consider next[0], starting at i = 1
前后缀不相同
假设next[:i]的值都已经计算完毕,现在要计算next[i]。
此时已知的条件是,s[:i]中最长相同前后缀长度为j,对应的前缀是s[:j],对应的后缀是s[i-j: i]。尝试同时延长前后缀的长度,也就是比较s[j]和s[i]的值。
如果s[j] != s[i],代表着同时延展之前的前后缀的方案不可行,则需要回退 j。
while (j > 0 and s[i] != s[j]):
j = next[j - 1]
while loop 的条件很好理解,但是回退的条件较为复杂。正常情况下,回退似乎应该是一步一步进行的,但在这里 j -= 1 由于前后缀的特性,显然不能奏效。
我们进行回溯的基础是,希望之前已经找到的相同前后缀能够提供一些回溯时的优势。
例子1:
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 模式串 | a | a | a | a | b | a | a | a | c |
| 前缀表 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 |
在模式串 aaaabaaac 中,当遍历到 c 的时候,i=8, j=3。此时发现 s[j] != s[i],于是回溯 j = next[j-1] = next[2] = 2。
我们试图回溯 j 的时候,已知虽然 s[j] != s[i],但在 c 之前有长度为3的相同前后缀 aaa。我们希望在这个子串 aaa 中寻找相同前后缀。
如果
- 能找到这个子串(前后缀)中对称的部分,即下标范围为 [0, 1] 的子串 aa 与 下标范围为 [6, 7] 的子串 aa 相等,
- 同时找到
s[j] == s[i],则意味着还是存在长度为 2+1=3 的相同前后缀
所以,我们才会希望回溯 j = next[j - 1]。
例子2:
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 模式串 | a | b | c | d | e | a | b | c | f |
| 前缀表 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 |
在模式串 abcdeabcf 中,当遍历到 f 的时候,i=8, j=3。此时发现 s[j] != s[i],于是回溯 j = next[j-1] = next[2] = 0。
我们试图回溯 j 的时候,已知虽然 s[j] != s[i],但在 f 之前有长度为3的相同前后缀 abc。我们希望在这个子串 abc 中寻找相同前后缀。
遗憾的是,该子串中没有相同前后缀,这意味着当前的子串 abcdeabcf 必然不可能出现任何长度超过1的相同前后缀。
前后缀相同
尝试同时延长前后缀的长度,也就是比较s[j]和s[i]的值。
如果s[j] == s[i],代表着同时延展之前的前后缀的方案可行,可以直接更新 j 和 next[i]。
整体代码
next[0] = 0
j = 1
i = 0
for i in range(1, len(s)):
while (j > 0 and s[i] != s[j]):
j = next[j - 1]
if (s[i] == s[j]):
j += 1
next[i] = j
28. 找出字符串中第一个匹配项的下标
题目链接 | 解题思路
有了回溯表(即 next 数组)之后,解题变得直接:双指针!
0. 调用函数,获取 needle 的 next 数组
- 定义文本串 haystack 的指针、模式串 needle 的指针,分别从头开始
- 当出现冲突时,回溯模式串的指针,直到两个指针所指向的字符相同,或者模式串指针回归原点。
- 当
j = len(needle)时,代表已经找到了整个 needle;否则,needle 并非 haystack 的子串。
- 出现冲突时,必须要用 while loop 回溯模式串中的指针
- for loop 中的更新与判定的顺序十分重要
class Solution:
def getNext(self, s: str) -> list:
next = [0] * len(s)
j = 0 # length of current max prefix and postfix
for i in range(1, len(s)):
while (j > 0 and s[i] != s[j]):
j = next[j - 1]
if s[i] == s[j]:
j += 1
next[i] = j
return next
def strStr(self, haystack: str, needle: str) -> int:
if len(needle) == 0:
return -1
next = self.getNext(needle)
curr_idx = 0
for i in range(len(haystack)):
while (curr_idx > 0 and haystack[i] != needle[curr_idx]):
curr_idx = next[curr_idx - 1]
if haystack[i] == needle[curr_idx]:
curr_idx += 1
if curr_idx == len(needle):
return i - len(needle) + 1
return -1
459. 重复的子字符串
题目链接 | 解题思路
暴力解法
遍历每个前缀,在输入中对任意前缀进行 find,并在输入的字符串中删除找到的前缀。如果存在前缀能够导致输入字符串为空字符,则成功找到。
复杂度太高,没有实际价值。(几乎没有过)
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
temp_s = s
flag = False
for i in range(len(s) - 1):
curr_word = s[:i+1]
while (temp_s != ""):
if temp_s.find(curr_word) == 0:
temp_s = temp_s[len(curr_word):]
else:
break
if temp_s == "":
flag = True
temp_s = s
return flag
移动匹配
利用了符合条件的字符串的结构特殊:
如果一个字符串由重复的子字符串组成,那么将两个这样的数拼起来(注意去头去尾,否则肯定能搜索到原本),必定也能在新的拼接字符串中找到原本的字符串。
但要注意调用库函数的复杂度(一般判断子字符串的库函数的实现 O ( m + n ) O(m+n) O(m+n))
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
concatenation = s[1:] + s[:-1]
return s in concatenation
KMP 应用
在由重复子串组成的字符串中,最长相等前后缀不包含的子串就是最小重复子串。
以上结论直接决定了 KMP 算法在这道题中的应用。
- 为什么 prefix/postfix 中缺失的部分即是最小重复单元?
数归法可以解决,此处给出 base case 的解释:
假设最长相同前后缀的长度为k,缺失长度为r = len(s) - kprefix[0:r] = postfix[0:r]postfix[0:r] = s[r:2*r]- 可得到
s[0:r] = s[r:2*r] - ⋯ ⋯ \cdots \cdots ⋯⋯
- 得到最小重复单元之后,如何求解?
令最小重复单元为rs,len(s) = rs * n,即原字符串由 n n n 个重复的最小单元组成。此时知道最长相同前后缀的长度为(n-1) * rs,如果len(s) % len(rs) == 0成立,即可知原字符串的确由重复子串组成。
class Solution:
def getNext(self, s: str) -> list:
next = [0] * len(s)
j = 0
for i in range(1, len(s)):
while (j > 0 and s[i] != s[j]):
j = next[j-1]
if s[i] == s[j]:
j += 1
next[i] = j
return next
def repeatedSubstringPattern(self, s: str) -> bool:
if len(s) == 0:
return False
next = self.getNext(s)
max_prefix_len = next[-1]
if max_prefix_len == 0:
return False
return len(s) % (len(s) - max_prefix_len) == 0
思路
注意以上的推导过程都只是充分条件,即如果原字符串的确是由重复子串组成,则满足移动匹配、KMP 算法的条件。然而,必要条件没有被证明,即不是由重复子串组成的字符串不能满足这些条件。b站评论大神的证明放在文件夹里了。