树（Tree）——Java语言

一，简单介绍

树（Tree），这种数据结构，自己可能平时没有很注重算法的锻炼，因此对于树，大多存在于知道和会用的程度（不是很熟练），因此自己准备好好重新捋一捋。毕竟树这个数据结构太重要了。
总结的内容是基于《大话数据结构》一书，写的挺不错的，语言简洁，还有点小故事帮助你加深理解。图片主要来源《大话数据结构》和网络

二，什么是树（Tree）

  树是一种一对多的数据结构，线性表，栈，队列，串都是一对一的线性数据结构。

2.1 树的定义：

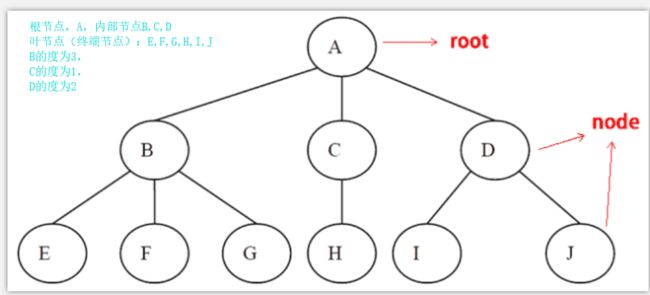
树（Tree）是n（n>=0）个结点的有限集。n=0时，称为空树。在任意一颗非空树中：
（1）有且仅有一个结点被称为根（Root）
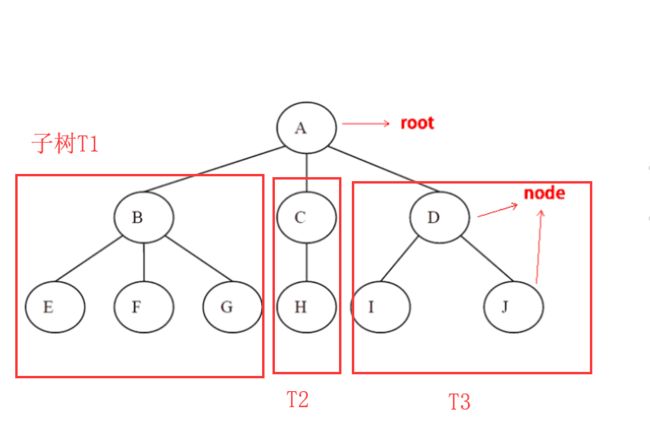
（2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1,T2,……,其中每一个集合本身又是一棵树，并且称为根的子树。
解释来源：《大话数据结构》

解释：

• 每个集合本身是一棵树：这本图中，表现为E,F,G和他们的根B构成了一棵树。

• 互不相交可以理解为，两个树之间不会有交叉，如果C到G有连线，就是错误的，因为他们交叉了。

2.2 结点的分类

树的结点包含一个数据元素及若干指向其子树的分支。

• 度：结点拥有的子树。
• 叶结点或终端结点：度为0的结点。
• 非终端结点或分支结点：度不为0的结点。
• 除根结点外，分支结点也称为内部结点。
• 树的度：树内各结点的度的最大值。
  

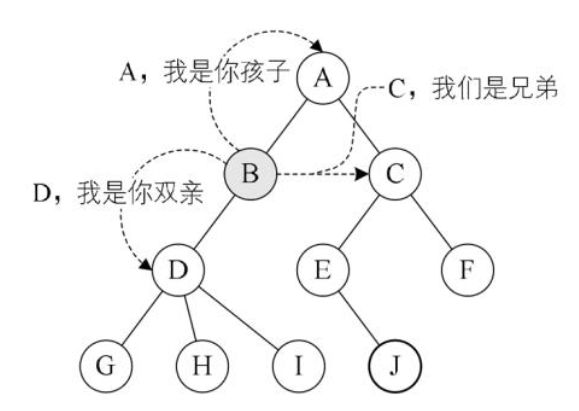
2.3 结点之间的关系

图片来源：《大话数据结构》

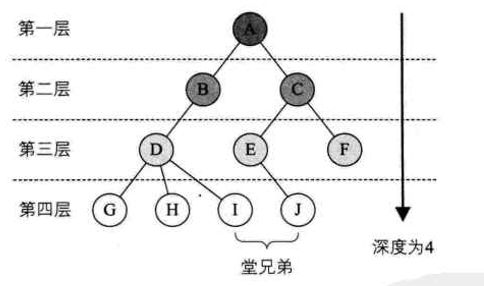
2.4 树的深度

树中结点的最大层次称为树的深度或高度。

2.4 森林

森林是m(m>=0)棵互不相交的树的集合。
树中每个结点而言，其子树的集合即为森林。T1,T2,T3即可理解为森林。

三，二叉树

  首先，java中有树这种封装好的数据结构吗？
答案是：肯定是有的。很多地方都蕴含在树这种数据结构，TreeMap，TreeSet,TreeNode，很多其他的数据结构中也使用了树这种数据结构。但是，这些蕴含树的封装好的类，和我们需要使用的，那种较为简单的树有相比，复杂的多。因此，二叉树还是需要自己进行构建。

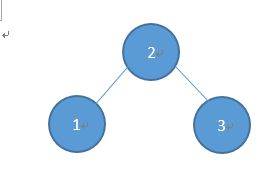
3.1 用java构建一个二叉树：

• 结点定义

public class TreeNode {
    private int value;//结点的值
    private TreeNode node;
    private TreeNode left;//左子结点
    private TreeNode right;//右子结点

    /**
     *getter and setter方法
     */
}

public class TreeDemo {
    public static void main(String[] args) {
        //二叉树的组装
        TreeNode treeNode = new TreeNode(2);
        TreeNode treeNode1 = new TreeNode(1);
        TreeNode treeNode2 = new TreeNode(3);
        treeNode.setLeft(treeNode1);
        treeNode.setRight(treeNode2);
    }
}

这样的代码就完成了一个如图的二叉树的构建。

3.2 二叉树的定义

二叉树是n (n>=0) 个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两棵互不相交的，分别称为根结点的左子树和右子树的二叉树组成。

二叉树适合的建模场景:开关，0和1，真和假，上和下，对与错，正面与反面。

3.3 二叉树特点

• 每个结点只有最多两棵子树，所以二叉树中不存在度大于2的结点。
• 左子树和右子树是有顺序的。左小右大。
• 即使只有一个子树也需要区别是左子树还是右子树。

3.4 特殊二叉树

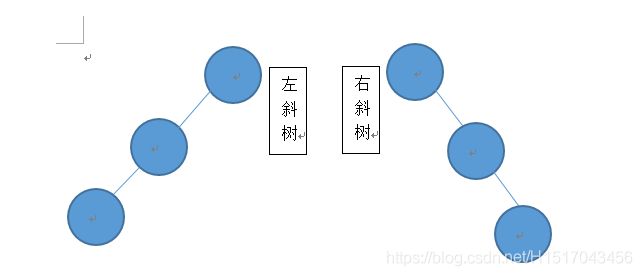
3.4.1 斜树

  所有的结点都只有左子树的二叉树叫左斜树。反之，称为右斜树。结点个数 = 结点深度

3.4.2 满二叉树

一棵二叉树中，所有的分支节点都存在左右子树，并且所有的叶子都在同一层上，这样的二叉树称为满二叉树。

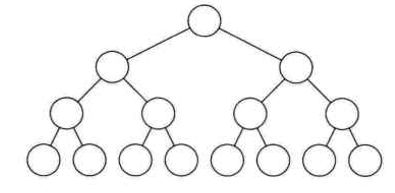
特点：（1）叶子在最下一层（2）非叶子节点的度一定是2.（3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子个数最多。

3.4.3 完全二叉树

对于一棵具有n个结点的二叉树按层序编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这颗二叉树称为完全二叉树。完全二叉树在缺失时，只能缺失右结点。

四、遍历二叉树

4.1 前序遍历

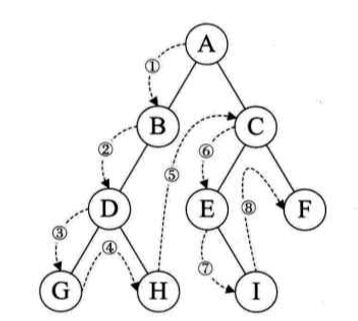
遍历规则：若二叉树是空树，则空操作返回，否则先访问根结点，然后前序遍历左子树，在前序遍历右子树。（根—》左—》右）

顺序：

代码：

public class TreeDemo {
    public static void main(String[] args) {
        //二叉树的组装
        TreeNode treeNodeA = new TreeNode("A");
        TreeNode treeNodeB = new TreeNode("B");
        TreeNode treeNodeC = new TreeNode("C");
        TreeNode treeNodeD = new TreeNode("D");
        TreeNode treeNodeE= new TreeNode("E");
        TreeNode treeNodeF = new TreeNode("F");
        TreeNode treeNodeG = new TreeNode("G");
        TreeNode treeNodeH = new TreeNode("H");
        TreeNode treeNodeI = new TreeNode("I");
        treeNodeA.setLeft(treeNodeB);
        treeNodeA.setRight(treeNodeC);
        treeNodeB.setLeft(treeNodeD);
        treeNodeD.setLeft(treeNodeG);
        treeNodeD.setRight(treeNodeH);
        treeNodeC.setLeft(treeNodeE);
        treeNodeC.setRight(treeNodeF);
        treeNodeE.setRight(treeNodeI);
        preOrderTraverse(treeNodeA);
    }
    //前序遍历法,递归实现
    static void preOrderTraverse(TreeNode node){
        if(node==null){
            return;
        }
        System.out.print(node.getValue()+"->");
        preOrderTraverse(node.getLeft());
        preOrderTraverse(node.getRight());
    }
}

4.2 中序遍历算法

遍历规则：中序遍历根节点的左子树，然后访问根节点，最后在是右子树。（顺序：左—》中—》右）

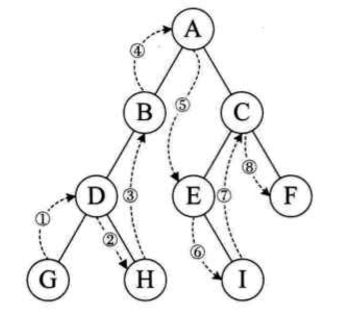
代码：

    //中序遍历，递归实现
    static void InOrderTraverse(TreeNode node){
        if(node==null){
            return;
        }
        InOrderTraverse(node.getLeft());
        System.out.print(node.getValue()+"->");
        InOrderTraverse(node.getRight());
    }

4.3 后序遍历

规则：若树是空，则返回空操作，否则就是从左到右先叶子节点后根节点的顺序。（左——》右——》根）

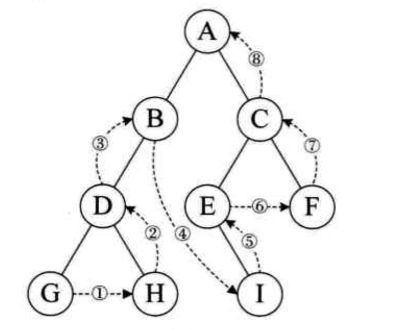
代码：

    //后序遍历
    static void PostOrderTraver(TreeNode node){
        if(node == null){
            return;
        }
        PostOrderTraver(node.getLeft());
        PostOrderTraver(node.getRight());
        System.out.print(node.getValue()+"->");
    }

五、一道根据前中序遍历重构二叉树的面试题

题目描述：
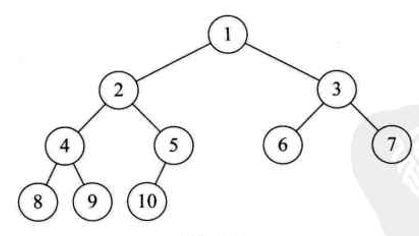
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。
来源：牛客网

5.1思路解析：

前序遍历：根，左，右（前序遍历来确定根）
中序遍历：左，中，右（中序遍历确定左右孩子）

5.1.1 左边子树的确定

1，首先，根据前序遍历找到整个树的根结点。题中为 1。
2，由中序遍历通过根结点分割左右子树。1的左子树的结点有：4,7，2。有子树的结点有5,3,8,6。
3，对于左子树的结点：4,7,2。由前序遍历1,2可知，2是1的左孩子结点，而4,7则应该为孙子结点，同时，4,7，应该是2的子结点或孙子结点。
4，由前序遍历2,4可知，4为2的左孩子。
5，由前序遍历1,2,4,7可知，7为4的子节点。由中序遍历4,7可知，7在4的右边，为4的右孩子。
至此，左边子树构建完成：

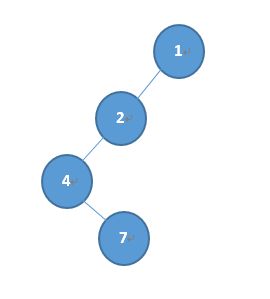
5.1.2右边子树的确定

1，由根结点在中序遍历中的位置：4,7,2,1,5,3,8,6。可知，右边子树的节点还剩5,3,8,6。
2，根据前序遍历：1,2,4,7,3,5,8,6可知，3是1的右子结点。

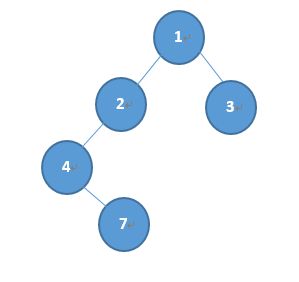
3，,由3在中序遍历5,3,8,6的结果可知，5是3的左子结点。而8和6的位置，这里可能需要特别区分一下。不能根据8在3的右边就判断为右子树。
4，在前序遍历3,5,6,8中可以看到6在8的前面即6为8的双亲节点。而由中序遍历5,3,8,6可知，8为6的左子节点。

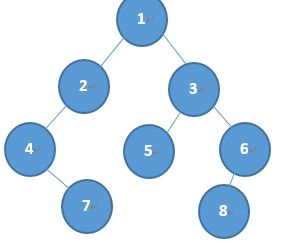
代码实现

这里我们用了一个类似于递归的思想，先通过先序遍历找根，再通过中序遍历找左右子结点，这样循环往复。
因此，重建的代码可以这样来设计：

    public static TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        if(pre.length==0&&in.length==0){
            return null;
        }
        //前序遍历序列{1,2,4,7,3,5,6,8}       中序遍历序列{4,7,2,1,5,3,8,6}
        //由前序获得根节点
        TreeNode treeRoot = new TreeNode(pre[0]);
        //在通过中序遍历来分割左右子树
        for(int i = 0;i<in.length;i++){
            if(pre[0] == in[i]){
                //递归的进行左右子树的根，左结点，右结点的分割
                //进行左子树的构建和分割
                treeRoot.left = reConstructBinaryTree(Arrays.copyOfRange(pre,1,i+1),Arrays.copyOfRange(in,0,i));
                treeRoot.right = reConstructBinaryTree(Arrays.copyOfRange(pre,i+1,pre.length),Arrays.copyOfRange(in,i+1,in.length));
            }
        }
        return treeRoot;
    }