java 表达式树_Java基础——表达式二叉树的Java实现构建(构建+前序、中序、后序遍历)...
1 表达式二叉树
1.1 定义
二叉树:在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
表达式二叉树:存储表达式的二叉树。
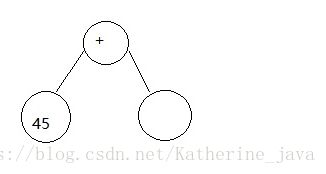
首先取出第一个数字45放在叶子节点,遇到“+”后将其放到分支节点,
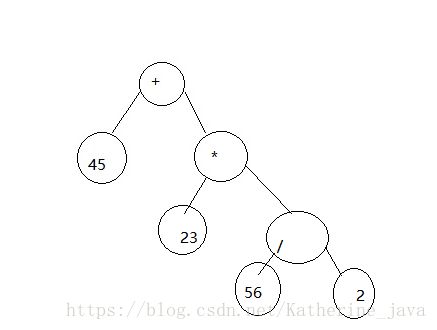
然后将“23”、“*”、“56”、“/”、“2”依次放入,
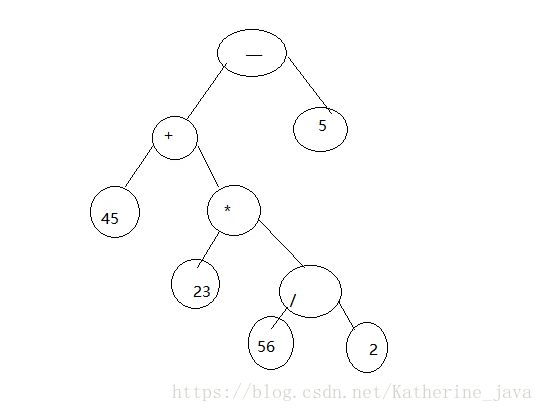
最后放入“-”、“5”,
1.2 构建步骤
1.创建节点对象;
2.辨析出操作符与数据,存放在相应的数组队列(类型为BinaryNode)中;
3.取出前两个数字和一个操作符,组成一个新的数字节点;
4.重复第3步,直到操作符取完为止;
5.让根节点等于最后一个节点。
2 构建
1.1 节点类
节点类包括三个参数:
private String data;
private BinaryNode left;
private BinaryNode right;
方法包括:
有参构造方法:在创建时必须初始化data
public BinaryNode(String data) {
this.data = data;
}
参数的set、get方法:
构建节点时,需要set其左右子树;
遍历二叉树时,需要get其左右子树、以及get其data。
1.2 二叉树类
package com.java8.binarytree;
import java.util.ArrayList;
import java.util.Stack;
/**
* 二叉树类
* 拥有属性为root,其构建后为数的根节点
*/
public class BinaryTree {
//根节点
private BinaryNode root = new BinaryNode(null);
public BinaryNode getRoot() {
return root;
}
//—————————————————————————————————创建 和 输出 1 ———————————————————————————————————————
/**
* 创建表达式二叉树
* @param str :输入为字符串
*/
public void build(String str) {
// numbers存储数字和节点,operations存储运算符号
// binaryNode用于构建数,snum用于接受个位十位百位数字
ArrayList numbers = new ArrayList<>();
ArrayList operations = new ArrayList<>();
BinaryNode binaryNode;
String snum = "";
//1.遍历str,找出所有的运算符和数字,存入numbers和operations数组队列
for (int i = 0; i < str.length(); i++) {
//1.1 取出字符串的各个字符
char ch = str.charAt(i);
//1.2 判断为符号还是数字,若为数字,则将s+=ch(防止数字为十位百位数)
if (ch >= '0' && ch <= '9') {
snum += ch + "";
}
//1.3 若为运算符,则将s和ch分别放入numbers、operations数组队列
else {
numbers.add(new BinaryNode(snum));
operations.add(new BinaryNode(ch + " "));
snum = "";
}
}
//1.4 将最后一位数字放入numbers数组队列
numbers.add(new BinaryNode(snum));
//2. 循环构建树,直至operations队列为空结束
while(!operations.isEmpty()) {
// 2.1从运算符中取出第一个作为node的数据;
binaryNode = operations.get(0);
operations.remove(0);
//2.2从数字取出第一个、第二个作为左、右;
binaryNode.setLeft(numbers.get(0));
binaryNode.setRight(numbers.get(1));
numbers.remove(0);
numbers.remove(0);
//2.3构建node,将其作为根节点root放回数字列表
root = binaryNode;
numbers.add(0, binaryNode);
}
}
/**
* 选择方式遍历输出表达式二叉树
* @param i:1——先序 2——中序 3——后序
*/
public void output(int i) {
switch (i) {
case 1:
System.out.println("输出——先序遍历:");
preOrder(root);
System.out.println("");
break;
case 2:
System.out.println("输出——中序遍历:");
midOrder(root);
System.out.println("");
break;
case 3:
System.out.println("输出——后序遍历:");
posOrder(root);
System.out.println("");
break;
}
}
//—————————————————————————————————遍历 3———————————————————————————————————————
/**
* 递归方法 —— 前序遍历的规则:
* (1)访问根节点
* (2)前序遍历左子树
* (3)前序遍历右子树
*/
public void preOrder(BinaryNode node) {
if (node != null) {
System.out.print(node.getData() + " ");
preOrder(node.getLeft());
preOrder(node.getRight());
}
}
/**
* 递归方法 —— 中序遍历的规则:
* (1)中序遍历左子树
* (2)访问根节点
* (3)中序遍历右子树
*/
public void midOrder(BinaryNode node) {
if (node != null) {
midOrder(node.getLeft());
System.out.print(node.getData() + " ");
midOrder(node.getRight());
}
}
/**
* 递归方法 —— 后序遍历的规则:
* (1)后序遍历左子树
* (2)后序遍历右子树
* (3)访问根节点
*/
public void posOrder(BinaryNode node) {
if (node != null) {
posOrder(node.getLeft());
posOrder(node.getRight());
System.out.print(node.getData() + " ");
}
}
/**
* 非递归方法 —— 前序遍历的规则:
* (1)访问根节点
* (2)前序遍历左子树
* (3)前序遍历右子树
*/
public void preOrder2() {
BinaryNode node = root;
Stack stack = new Stack<>();
ArrayList preList = new ArrayList<>();
while (node != null || stack.size() != 0) {
while (node != null) {
stack.push(node);
preList.add(node.getData());
node = node.getLeft();
}
if (stack.size() != 0) {
node = stack.pop();
node = node.getRight();
}
}
System.out.println("非递归——先序遍历:" + preList.toString());
}
/**
* 非递归方法 —— 中序遍历的规则:
* (1)中序遍历左子树
* (2)访问根节点
* (3)中序遍历右子树
*/
public void midOrder2() {
Stack stack = new Stack<>();
ArrayList midList = new ArrayList<>();
BinaryNode node = root;
while (node != null || stack.size() != 0) {
while (node != null) {
stack.push(node);
node = node.getLeft();
}
if (stack.size() != 0) {
node = stack.pop();
midList.add(node.getData());
node = node.getRight();
}
}
System.out.println("非递归——中序遍历: " + midList.toString());
}
//—————————————————————————————————测试 2———————————————————————————————————————
/**
* 输出检验函数,查看numbers和operations是否已经存入数据
* @param list:Node列表
*/
public void printList(ArrayList list) {
for (int i = 0; i < list.size(); i++) {
System.out.print(list.get(i));
System.out.print(" ");
}
}
/**
* 输出检验函数,Stack是否已经存入数据
* @param list:Node列表
*/
public void printList(Stack list) {
for (int i = 0; i < list.size(); i++) {
System.out.print(list.get(i).getData());
System.out.print(" ");
}
}
}
3 遍历
3.1 遍历方式
例子:45+23*56/2-5
先序遍历:- / * + 45 23 56 2 5
/**
* 递归方法 —— 前序遍历的规则:
* (1)访问根节点
* (2)前序遍历左子树
* (3)前序遍历右子树
*/
中序遍历:45 + 23 * 56 / 2 - 5
/**
* 递归方法 —— 中序遍历的规则:
* (1)中序遍历左子树
* (2)访问根节点
* (3)中序遍历右子树
*/
后序遍历:45 23 + 56 * 2 / 5 -
/**
* 递归方法 —— 后序遍历的规则:
* (1)后序遍历左子树
* (2)后序遍历右子树
* (3)访问根节点
*/
代码:
2.2中的BinaryTree中的第二部分
4 测试类
package com.java8.binarytree;
public class Manage {
public static void main(String[] args) {
//创建binaryTree对象,其初始包含data为null的root节点
BinaryTree binaryTree = new BinaryTree();
//build二叉树时,需要输入表达式的String
binaryTree.build("45+23*56/2-5");
//查看是否构建完成,获取现在的root节点
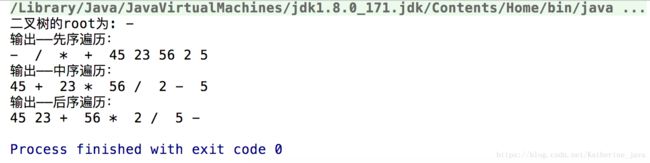
System.out.println("二叉树的root为: "+binaryTree.getRoot().getData());
binaryTree.output(1);
binaryTree.output(2);
binaryTree.output(3);
}
}