(七)Cauchy 积分公式及其推论
本文主要内容包括:
- 1. Cauchy 积分公式
- 2. Cauchy 积分公式的重要推论
-
- 2.1. 平均值定理
- 2.2. 最大模原理
1. Cauchy 积分公式
定理:设区域 D 的边界为复/单周线 Γ = C 0 ∪ C 1 − ⋯ \Gamma=C_0\cup C_1^-\cdots Γ=C0∪C1−⋯,函数 f ( z ) f(z) f(z) 在区域 D 内解析,在 D ‾ = D ∪ Γ \overline D=D\cup\Gamma D=D∪Γ 上连续,则有:
f ( z 0 ) = 1 2 π i ∮ Γ f ( z ) z − z 0 d z ( z 0 ∈ D ) f(z_0)=\dfrac{1}{2\pi i}\oint_\Gamma\dfrac{f(z)}{z-z_0}dz\qquad(z_0\in D) f(z0)=2πi1∮Γz−z0f(z)dz(z0∈D)右侧积分称作 Cauchy 积分。
证明:以 z 0 z_0 z0 为圆心,充分小的 ρ > 0 \rho>0 ρ>0 为半径作圆周 γ ρ \gamma_\rho γρ,使得 γ ρ \gamma_\rho γρ 完全含于 D,如图: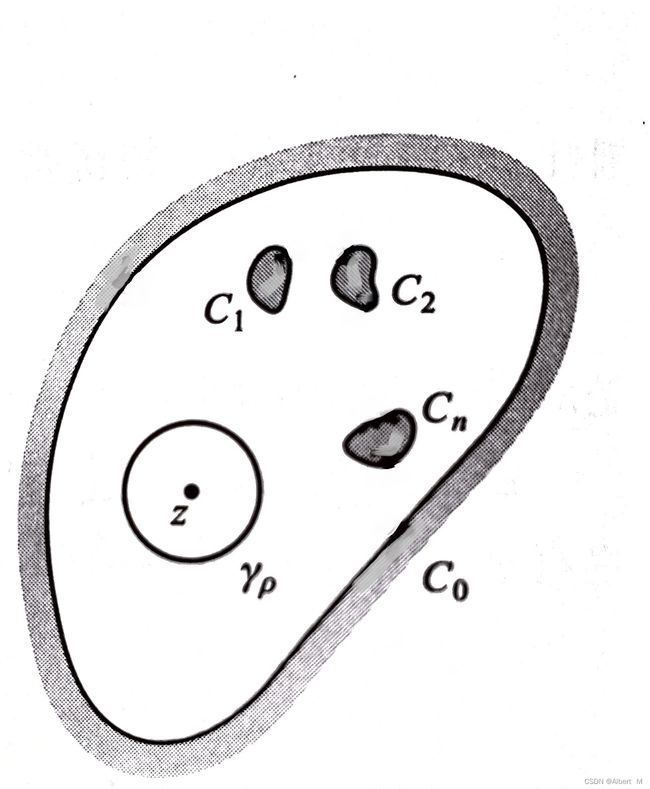
由于函数 f ( z ) f(z) f(z) 在 D D D 上连续,故
F o r ∀ ε > 0 , ∃ δ > 0 , s . t . w h e n ∣ z − z 0 ∣ = ρ < δ , ∣ f ( z ) − f ( z 0 ) ∣ < ε 2 π For~ \forall\varepsilon>0,\exist~\delta>0,~s.t.~when~ |z-z_0|=\rho<\delta,~|f(z)-f(z_0)|<\dfrac{\varepsilon}{2\pi} For ∀ε>0,∃ δ>0, s.t. when ∣z−z0∣=ρ<δ, ∣f(z)−f(z0)∣<2πε 又函数 f ( z ) z − z 0 \dfrac{f(z)}{z-z_0} z−z0f(z) 在 D \ { z 0 } D\backslash \{z_0\} D\{z0} 上解析,根据复合闭路原理有:
∮ Γ f ( z ) z − z 0 d z = ∮ γ ρ f ( z ) z − z 0 d z = ∮ γ ρ f ( z ) − f ( z 0 ) + f ( z 0 ) z − z 0 d z = ∮ γ ρ f ( z ) − f ( z 0 ) z − z 0 d z + f ( z 0 ) ∮ γ ρ 1 z − z 0 d z = ∮ γ ρ f ( z ) − f ( z 0 ) z − z 0 d z + f ( z 0 ) 2 π i \begin{aligned} \oint_\Gamma\dfrac{f(z)}{z-z_0}dz&=\oint_{\gamma_\rho}\dfrac{f(z)}{z-z_0}dz\\\\ &=\oint_{\gamma_\rho}\dfrac{f(z)-f(z_0)+f(z_0)}{z-z_0}dz\\\\ &=\oint_{\gamma_\rho}\dfrac{f(z)-f(z_0)}{z-z_0}dz+f(z_0)\oint_{\gamma_\rho}\dfrac{1}{z-z_0}dz\\\\ &=\oint_{\gamma_\rho}\dfrac{f(z)-f(z_0)}{z-z_0}dz+f(z_0)2\pi i \end{aligned} ∮Γz−z0f(z)dz=∮γρz−z0f(z)dz=∮γρz−z0f(z)−f(z0)+f(z0)dz=∮γρz−z0f(z)−f(z0)dz+f(z0)∮γρz−z01dz=∮γρz−z0f(z)−f(z0)dz+f(z0)2πi
那么
∣ ∮ γ ρ f ( z ) z − z 0 d z − f ( z 0 ) 2 π i ∣ = ∣ ∮ γ ρ f ( z ) − f ( z 0 ) z − z 0 d z ∣ ⩽ ∮ γ ρ ∣ f ( z ) − f ( z 0 ) z − z 0 ∣ ∣ d z ∣ < 1 ρ ε 2 π ⋅ 2 π ρ = ε \begin{aligned} \left|\oint_{\gamma_\rho}\dfrac{f(z)}{z-z_0}dz-f(z_0)2\pi i\right| &=\left|\oint_{\gamma_\rho}\dfrac{f(z)-f(z_0)}{z-z_0}dz\right| \\\\ &\leqslant\oint_{\gamma_\rho}\left|\dfrac{f(z)-f(z_0)}{z-z_0}\right||dz| \\\\ &<\dfrac{1}{\rho}\dfrac{\varepsilon}{2\pi}\cdot2\pi\rho=\varepsilon \end{aligned} ∮γρz−z0f(z)dz−f(z0)2πi = ∮γρz−z0f(z)−f(z0)dz ⩽∮γρ z−z0f(z)−f(z0) ∣dz∣<ρ12πε⋅2πρ=ε即
∮ Γ f ( z ) z − z 0 d z = lim ρ → 0 ∮ γ ρ f ( z ) z − z 0 d z = f ( z 0 ) 2 π i \oint_\Gamma\dfrac{f(z)}{z-z_0}dz=\lim_{\rho\rightarrow0}\oint_{\gamma_\rho}\dfrac{f(z)}{z-z_0}dz=f(z_0)2\pi i ∮Γz−z0f(z)dz=ρ→0lim∮γρz−z0f(z)dz=f(z0)2πi故定理得证。
2. Cauchy 积分公式的重要推论
2.1. 平均值定理
定理(平均值定理): 设函数在圆盘 D : ∣ z − z 0 ∣ < R D:|z-z_0|
D:∣z−z0∣<R 内解析,在闭圆盘 D ‾ = D ∪ ∂ D \overline D=D\cup\partial D D=D∪∂D 上连续,则 圆心处的函数值等于函数在圆周上值的算数平均值,即
f ( z 0 ) = 1 2 π ∫ 0 2 π f ( z 0 + R e i ϕ ) d ϕ f(z_0)=\dfrac{1}{2\pi}\int_0^{2\pi}f(z_0+Re^{i\phi})d\phi f(z0)=2π1∫02πf(z0+Reiϕ)dϕ
证明:圆周线的参数方程为: ζ = z 0 + R e i ϕ , ( 0 ⩽ ϕ ⩽ 2 π ) \zeta=z_0+Re^{i\phi},\quad(0\leqslant \phi\leqslant 2\pi) ζ=z0+Reiϕ,(0⩽ϕ⩽2π)则
d ζ = i R e i ϕ d ϕ d\zeta=iRe^{i\phi}d\phi dζ=iReiϕdϕ根据 Cauchy 积分公式
f ( z 0 ) = 1 2 π i ∮ ∂ D ( ζ ) ζ − z 0 d ζ = 1 2 π i ∫ 0 2 π f ( z 0 + R e i ϕ ) R e i ϕ i R e i ϕ d ϕ = 1 2 π ∫ 0 2 π f ( z 0 + R e i ϕ ) d ϕ f(z_0)=\dfrac{1}{2\pi i}\oint_{\partial D}\dfrac{(\zeta)}{\zeta-z_0}d\zeta= \dfrac{1}{2\pi i}\int_0^{2\pi}\dfrac{f(z_0+Re^{i\phi})}{Re^{i\phi}}iRe^{i\phi}d\phi= \dfrac{1}{2\pi}\int_0^{2\pi}f(z_0+Re^{i\phi})d\phi f(z0)=2πi1∮∂Dζ−z0(ζ)dζ=2πi1∫02πReiϕf(z0+Reiϕ)iReiϕdϕ=2π1∫02πf(z0+Reiϕ)dϕ(证毕).
2.2. 最大模原理
引理:设函数在圆盘 D : ∣ z − z 0 ∣ < R D:|z-z_0|
D:∣z−z0∣<R 内解析,在闭圆盘 D ‾ = D ∪ ∂ D \overline D=D\cup\partial D D=D∪∂D 上连续,若 ∣ f ( z 0 ) ∣ = max z ∈ D ( ∣ f ( z ) ∣ ) = M |f(z_0)|=\max_{z\in D}(|f(z)|)=M ∣f(z0)∣=z∈Dmax(∣f(z)∣)=M则在圆盘 D 内,复函数 f ( z ) f(z) f(z) 为常数。
证明:(反证法)由于函数在圆盘内解析,若它的模在圆盘内为常数,则它本身在圆盘上也为常数。
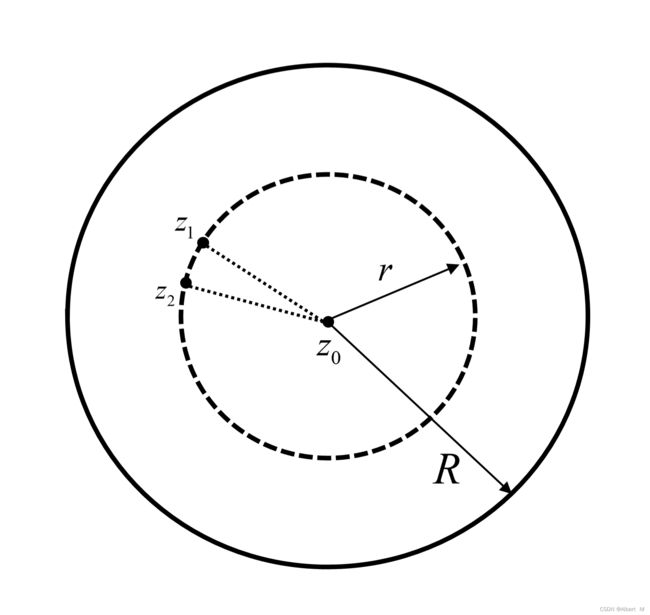
设 ∃ z 1 = z 0 + r e i θ 1 ∈ D \ { z 0 } , s . t . ∣ f ( z 1 ) ∣ < ∣ f ( z 0 ) ∣ = M \exist~z_1=z_0+re^{i\theta_1}\in D\backslash\{z_0\},~s.t.~|f(z_1)|<|f(z_0)|=M ∃ z1=z0+reiθ1∈D\{z0}, s.t. ∣f(z1)∣<∣f(z0)∣=M记
∣ f ( z 1 ) ∣ = M − p ( p > 0 ) |f(z_1)|=M-p\quad(p>0) ∣f(z1)∣=M−p(p>0)由于 f ( z ) f(z) f(z) 在 ∣ z − z 0 ∣ = r |z-z_0|=r ∣z−z0∣=r 上连续,故 ∣ f ( z ) ∣ |f(z)| ∣f(z)∣ 在该圆上也连续,取 z 2 = z 0 + r e i θ 2 z_2=z_0+re^{i\theta_2} z2=z0+reiθ2
∀ ε > 0 , ∃ δ > 0 , s . t . w h e n ∣ θ 1 − θ 2 ∣ < δ , ∣ ∣ f ( z 2 ) ∣ − ∣ f ( z 1 ) ∣ ∣ < ε 2 \forall\varepsilon>0,~\exist~\delta>0,s.t.~when~|\theta_1-\theta_2|<\delta,~|~|f(z_2)|-|f(z_1)|~|<\dfrac{\varepsilon}{2} ∀ε>0, ∃ δ>0,s.t. when ∣θ1−θ2∣<δ, ∣ ∣f(z2)∣−∣f(z1)∣ ∣<2ε不妨取 ε = p \varepsilon=p ε=p,此时有:
∣ f ( z 2 ) ∣ < M − p 2 |f(z_2)|
M = ∣ f ( z 0 ) ∣ = 1 2 π ∣ ∫ 0 2 π f ( z ) d θ ∣ ⩽ 1 2 π ∫ 0 2 π ∣ f ( z ) ∣ d θ = 1 2 π ∫ θ 1 − δ θ 2 + δ ∣ f ( z ) ∣ d θ + 1 2 π ∫ [ 0 , 2 π ] \ [ θ 1 − δ , θ 1 + δ ] ∣ f ( z ) ∣ d θ < 1 2 π ∫ θ 1 − δ θ 2 + δ ( M − p 2 ) d θ + 1 2 π ∫ [ 0 , 2 π ] \ [ θ 1 − δ , θ 1 + δ ] M d θ = ( M − p 2 ) δ π + ( π − δ ) M π = M − p δ 2 π < M \begin{aligned} M=|f(z_0)|&=\dfrac{1}{2\pi}\left|\int_0^{2\pi}f(z)d\theta\right|\\\\ &\leqslant\dfrac{1}{2\pi}\int_0^{2\pi}\left|f(z)\right|d\theta\\\\ &=\dfrac{1}{2\pi}\int_{\theta_1-\delta}^{\theta_2+\delta}\left|f(z)\right|d\theta+\dfrac{1}{2\pi}\int_{[0,2\pi]\backslash[\theta_1-\delta,\theta_1+\delta]}\left|f(z)\right|d\theta \\\\ &<\dfrac{1}{2\pi}\int_{\theta_1-\delta}^{\theta_2+\delta}\left(M-\dfrac{p}{2}\right)d\theta+\dfrac{1}{2\pi}\int_{[0,2\pi]\backslash[\theta_1-\delta,\theta_1+\delta]}Md\theta \\\\ &=\left(M-\dfrac{p}{2}\right)\dfrac{\delta}{\pi}+\left(\pi-\delta\right)\dfrac{M}{\pi}\\\\ &=M-\dfrac{p\delta}{2\pi}
\quad
定理(最大模原理):设函数 f ( z ) f(z) f(z) 在区域 D 内解析,又 f ( z ) f(z) f(z) 不是常函数,则 ∣ f ( z ) ∣ |f(z)| ∣f(z)∣ 在区域 D 内没有最大值。
证明:(反证法)记
max z ∈ D ∣ f ( z ) ∣ = M \max_{z\in D}|f(z)|=M z∈Dmax∣f(z)∣=M若 M = + ∞ M=+\infty M=+∞,则定理成立,若 M < + ∞ M<+\infty M<+∞,设
∃ z 0 ∈ D , s . t . ∣ f ( z 0 ) ∣ = M \exist~z_0\in D,~s.t.~|f(z_0)|=M ∃ z0∈D, s.t. ∣f(z0)∣=M 那么,根据引理可得在圆盘 C 1 = { z ∣ ∣ z − z 0 ∣ < r 1 } ⊂ D C_1=\{z|~|z-z_0|

那么所有圆盘 C k : ∣ z − z k ∣ < d C_k:|z-z_k|
∣ f ( z ∗ ) ∣ = ∣ f ( z 0 ) ∣ = M |f(z^*)|=|f(z_0)|=M ∣f(z∗)∣=∣f(z0)∣=M根据 z ∗ z^* z∗ 的任意性可知:
∣ f ( z ) ∣ = M , ( z ∈ D ) ⇒ f ( z ) = C o n s t |f(z)|=M,~(z\in D)\Rightarrow f(z)=Const ∣f(z)∣=M, (z∈D)⇒f(z)=Const矛盾,故原命题成立。
\quad
Remark:
\quad
1)在区域 D 内解析的函数,若其模在 D 内达到最大值,则此函数必为常数;
\quad
2)若 f ( z ) f(z) f(z) 在有界区域 D 内解析,在 D ‾ \overline D D 上连续,则 ∣ f ( z ) ∣ |f(z)| ∣f(z)∣ 必在闭区域的边界上有最大模。