C++ 最大公约数与最小公倍数
(一)简单的两个正整数 求 最大公约数 (引入专题)
思路:
根据 “欧几里得算法” ,即 “辗转相除法” 原理如下:
| 题意: 求出 a , b 两个正整数的最大公约数 设 k = a / b, r = a % b 即 a = k * b + r 又设 d 为 a 和 b 的一个公约数 那么由 r = a - k * b, 可知 d 也是 r 的一个公约数 所以 d 是 b 和 r 的一个公约数 又因为 r = a % b, 所以 d 也是 b 和 a % b 的一个公约数 所以 d 是 a 和 b 的公约数,也是 b 和 a % b 的公约数 因为 d 的任意性,所以 a 和 b 的公约数 都是 b 和 a % b 的公约数 由 a = k * b + r ,同理可以证明: b 和 a % b 的公约数 都是 a 和 b 的公约数 所以 a 和 b 的公约数与 b 和 a % b 的公约数 全部相等,所以最大公约数也相等。 所以 Gcd(a,b) == Gcd(b,a % b) |
根据以上证明,得出规律:
如果 a < b 那么结果是 a 和 b 之间的数值交换 即 a % b = a, Gcd(b, a % b) == Gcd(b,a)
如果 a > b 那么 根据 Gcd(a,b) == (b, a%b) 进行规模的减小,此时需要一个递归边界
这个递归边界就是 : Gcd(a,0) 因为 0 和任意一个整数 a 的最大公约数 就是 a (注:不是 0)
所以总结如下:
1、 递归方式:Gcd(a,b) == Gcd(b,a % b)
2、递归边界: Gcd(a,0) == a
函数代码实现如下:
int Gcd(int a, int b)
{
if (b == 0)
return a;
else
return Gcd(b, a % b);
}化简写法:
int Gcd(int a, int b)
{
return !b ? a : Gcd(b, a % b);
}(一)解题源码:
#include
using namespace std;
int Gcd(int a, int b)
{
return !b ? a : Gcd(b, a % b);
}
int main()
{
int a, b;
cin >> a >> b;
cout << Gcd(a, b) << endl;
return 0;
} (二)求 多个数值 的最大公约数
思路:
根据 (一)简单的两个正整数 求 最大公约数 (引入专题) 的 对两个正整数的最大公约数 证明详解,我们可以得知:
设 求出 a,b,c 三个数值的 最大公约数
我们 根据 (一) 最后得出 Gcd(a,b) == d ,最后 b == 0
这时,我们可以换个角度去理解 求出了 a 和 b 最大公约数 d 后,令 b == c
此时 b != 0,继续 辗转相除 最后 b == 0,得出 最终就可以得出 a,b,c 三个数值的 最大公约数了
代码实现如下:
#include
using namespace std;
int Gcd(int a, int b)
{
return !b ? a : Gcd(b, a % b);
}
int main()
{
int n;
int num; // 需求的数字
int a = 0, b = 0;
int gcd = 0; // 存储 结果 最大公约数
cin >> n; // 输入 需求 的 n 个整数
for (int i = 0; i < n; i++) {
cin >> num; // 输入 需求的数字
if (!a) // 判断 a 是否为 0,是 则 赋值新的需求数字
a = num;
else
b = num; // 判断 b 是否为 0,是 则 赋值新的需求数字
if (i >= 1) { // 输入完 两个 需求的数字后 开始 求 公约数
gcd = Gcd(a, b); // 求得公约数后,存储好结果
a = gcd; // 由于函数的性质,变的是形参a,所以我们要 做到 实参与形参一致
b = 0; // 由于函数的性质,变的是形参b,所以我们要 做到 实参与形参一致
}
}
cout << gcd << endl; // 输出结果
return 0;
} (三) 求两个正整数的最小公倍数
思路:
最小公倍数的求解,是在最大公约数的基础上进行的,当得到 a 和 b 的最大公约数 d 后,
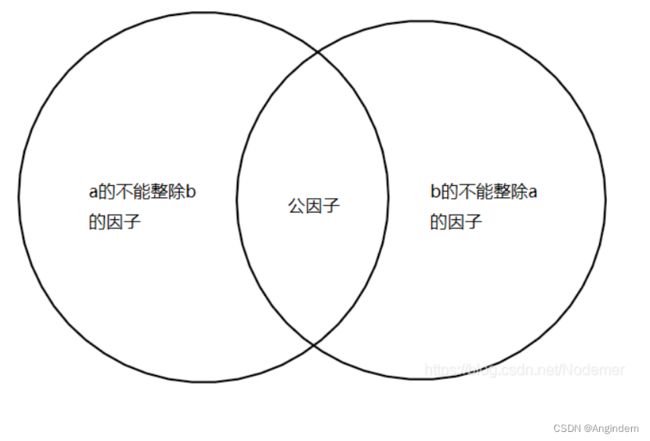
我们的最小公倍数就是 a * b / d,这个公式我们可以通过集合去理解:
通过上面的图,我们可以知道, 最大公约数 d 是 a 和 b 的交集,而 最小公倍数 就是我们 a 和 b的并集,所以要得到最小公倍数,a * b 时,会使 公因子 多计算了一遍,因此要除掉一次公因子,所以就得到了 最小公倍数: a * b / d
又由于 a * b 时,当数值比较大时,可能会使 计算结果溢出,所以更恰当的写法是:a / d * b
因为 d 为 a 和 b 的最大公约数,所以, a / d 一定可以整除。
所以最小公倍数的函数是:
int Lcm(int a, int b)
{
return a / Gcd(a, b) * b;
}所以代码实现如下:
#include
using namespace std;
int Gcd(int a, int b)
{
return !b ? a : Gcd(b, a % b);
}
int Lcm(int a, int b)
{
return a / Gcd(a, b) * b;
}
int main()
{
int a, b;
cin >> a >> b;
cout << Lcm(a, b) << endl;
return 0;
} (四)求多个正整数的最小公倍数
思路:
与求多个数值的最大公约数的思路大致相似,当我们求出其中的两个数值的最小公倍数后,将该最小公倍数看做独立的一个数值,相继与剩余的多个数值,进行相继的求最小公倍数数值,最后得出结果多个数值的最小公倍数。
代码实现如下:
#include
using namespace std;
int Gcd(int a, int b)
{
return !b ? a : Gcd(b, a % b);
}
int Lcm(int a, int b)
{
return a / Gcd(a, b) * b;
}
int main()
{
int n;
int num;
int lcm = 0;
int a = 0, b = 0;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> num;
if (!a)
a = num;
else
b = num;
if (i >= 1) {
lcm = Lcm(a, b);
a = lcm;
b = 0;
}
}
cout << lcm << endl;
return 0;
}