Go语言-数据结构与算法

Go语言 数据结构与算法

20.4 稀疏 sparsearray 数组

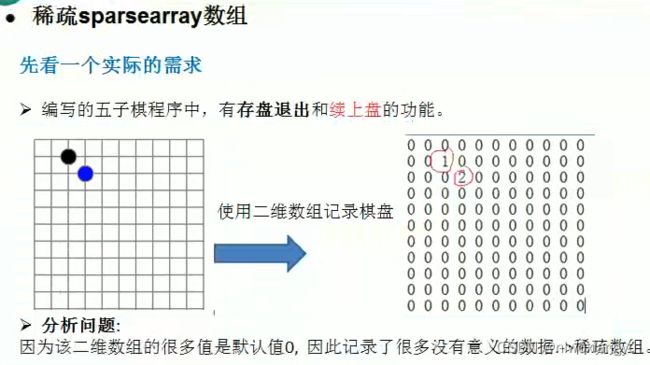
20.4.1 先看一个实际的需求

 编写的五子棋程序中，有存盘退出和续上盘的功能

稀疏数组的处理方法是 :

1) 记录数组一共有几行几列，有多少个不同的值

2) 思想：把具有不同值的元素的行列及值记录在一个小规模的数组中，从而 缩小程序 的规模

20.4.4 应用实例

1) 使用稀疏数组，来保留类似前面的二维数组 ( 棋盘、地图等等 )

2) 把稀疏数组存盘，并且可以从新恢复原来的二维数组数

3) 整体思路分析

4) 代码实现

package main

import "fmt"

type ValNode struct {
	row int
	col int
	val int
}

func main() {
	//1. 先创建一个原始数组
	var chessMap [11][11]int
	chessMap[1][2] = 1 // 黑子
	chessMap[2][3] = 2 // 蓝子
	//2. 输出看看原始的数组
	for _, v := range chessMap {
		for _, v2 := range v {
			fmt.Printf("%d\t", v2)
		}
		fmt.Println()
	}
	//3. 转成稀疏数组。想-> 算法
	// 思路
	//(1). 遍历 chessMap, 如果我们发现有一个元素的值不为 0，创建一个 node 结构体
	//(2). 将其放入到对应的切片即可
	var sparseArr []ValNode

	//标准的一个稀疏数组应该还有一个 记录元素的二维数组的规模(行和列，默认值)
	//创建一个 ValNode 值结点
	valNode := ValNode{
		row: 11,
		col: 11,
		val: 0,
	}

	sparseArr = append(sparseArr, valNode)
	for i, v := range chessMap {
		for j, v2 := range v {
			if v2 != 0 {
				//创建一个 ValNode 值结点
				valNode := ValNode{
					row: i,
					col: j,
					val: v2,
				}
				sparseArr = append(sparseArr, valNode)
			}
		}
	}

	//输出稀疏数组
	fmt.Println("当前的稀疏数组是:::::")
	for i, valNode := range sparseArr {
		fmt.Printf("%d:%d %d %d\n", i, valNode.row, valNode.col, valNode.val)
	}

	//将这个稀疏数组，存盘 d:/chessmap.data

	//如何恢复原始的数组

	//1. 打开这个 d:/chessmap.data => 恢复原始数组.
	//2. 这里使用稀疏数组恢复

	// 先创建一个原始数组
	var chessMap2 [11][11]int

	// 遍历 sparseArr [遍历文件每一行]
	for i, valNode := range sparseArr {
		if i != 0 {
			//跳过第一行记录值
			chessMap2[valNode.row][valNode.col] = valNode.val
		}
	}

	// 看看 chessMap2 是不是恢复
	fmt.Println("恢复后的原始数据......")
	for _, v := range chessMap2 {
		for _, v2 := range v {
			fmt.Printf("%d\t", v2)
		}
		fmt.Println()
	}
}

PS D:\Workspace\Go\src\projects\gin-demo> go run test.go
0       0       0       0       0       0       0       0       0       0       0
0       0       1       0       0       0       0       0       0       0       0
0       0       0       2       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
当前的稀疏数组是:::::
0:11 11 0 %!d(MISSING)
1:1 2 1 %!d(MISSING)
2:2 3 2 %!d(MISSING)
恢复后的原始数据......
0       0       0       0       0       0       0       0       0       0       0
0       0       1       0       0       0       0       0       0       0       0
0       0       0       2       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0
0       0       0       0       0       0       0       0       0       0       0

对老师的稀疏数组的改进

1) 将构建的稀疏数组，存盘 chessmap.data

2) 在恢复原始二维数组，要求从文件 chessmap.data 读取。

20.5 队列(queue)

20.5.1 队列的应用场景

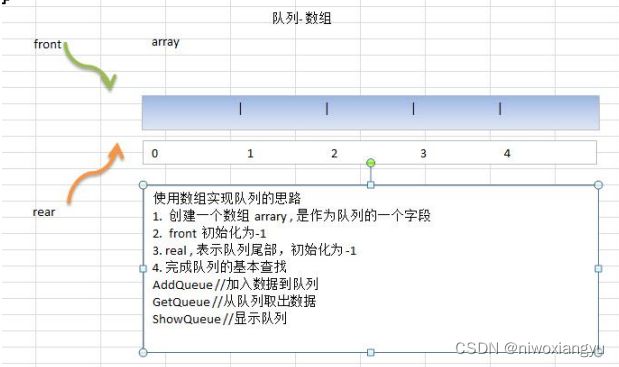
20.5.3 数组模拟队列

先完成一个非环形的队列 ( 数组来实现 )

思路分析：

 代码实现：

package main

import (
	"errors"
	"fmt"
	"os"
)

//使用一个结构体管理队列
type Queue struct {
	maxSize int
	array   [5]int // 数组=>模拟队列
	front   int    // 表示指向队列首
	rear    int    // 表示指向队列的尾部
}

//添加数据到队列
func (this *Queue) AddQueue(val int) (err error) {
	//先判断队列是否已满
	if this.rear == this.maxSize-1 { //重要重要的提示; rear 是队列尾部(含最后元素)
		return errors.New("queue full")
	}

	this.rear++ // rear 后移
	this.array[this.rear] = val
	return
}

//从队列中取出数据
func (this *Queue) GetQueue() (val int, err error) {
	//先判断队列是否为空
	if this.rear == this.front { //队空
		return -1, errors.New("queue empty")
	}
	this.front++
	val = this.array[this.front]
	return val, err
}

//显示队列, 找到队首，然后到遍历到队尾
func (this *Queue) ShowQueue() {
	fmt.Println("队列当前的情况是:")
	//this.front 不包含队首的元素
	for i := this.front + 1; i <= this.rear; i++ {
		fmt.Printf("array[%d]=%d\t", i, this.array[i])
	}
	fmt.Println()
}

//编写一个主函数测试，测试
func main() {
	//先创建一个队列
	queue := &Queue{
		maxSize: 5, front: -1, rear: -1,
	}

	var key string
	var val int
	for {
		fmt.Println("1. 输入 add 表示添加数据到队列")
		fmt.Println("2. 输入 get 表示从队列获取数据")
		fmt.Println("3. 输入 show 表示显示队列")
		fmt.Println("4. 输入 exit 表示退出")

		fmt.Scanln(&key)
		switch key {
		case "add":
			fmt.Println("输入你要入队列数")
			fmt.Scanln(&val)
			err := queue.AddQueue(val)
			if err != nil {
				fmt.Println(err.Error())
			} else {
				fmt.Println("加入队列ok")
			}
		case "get":
			val, err := queue.GetQueue()
			if err != nil {
				fmt.Println(err.Error())
			} else {
				fmt.Println("从队列中取出了一个数=", val)
			}
		case "show":
			queue.ShowQueue()
		case "exit":
			os.Exit(0)
		}
	}
}

PS D:\Workspace\Go\src\projects\gin-demo> go run test.go
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
1
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
add
输入你要入队列数
1
加入队列ok
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
get
从队列中取出了一个数= 1
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
4. 输入 exit 表示退出程序
show
队列当前的情况是:

1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
队列当前的情况是:
exit status 0xc000013a
PS D:\Workspace\Go\src\projects\gin-demo> go run test.go
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
add
输入你要入队列数
1
加入队列ok
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
get
从队列中取出了一个数= 1
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
show
队列当前的情况是:

1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出程序
exit
PS D:\Workspace\Go\src\projects\gin-demo>

对上面代码的小结和说明 ：

1 ） 上面代码实现了基本队列结构，但是 没有有效的利用数组 空间

2 ） 请思考，如何使用数组 实现一个环形的队列

20.5.4 数组模拟环形队列

分析思路 :

1) 什么时候表示队列满 (tail + 1) % maxSize hea d

2) tail == head 表示空

3) 初始化时， tail = 0 head = 0

4) 怎么统计该队列有多少个元素 (tail + maxSize - head ) % maxSize

代码实现 ：

package main

import (
	"errors"
	"fmt"
	"os"
)

//使用一个结构体管理环形队列
type CircleQueue struct {
	maxSize int    // 4
	array   [5]int // 数组
	head    int    // 指向队列队首 0
	tail    int    // 指向队尾
}

//如队列 AddQueue(push) GetQueue(pop)
//入队列
func (this *CircleQueue) Push(val int) (err error) {
	if this.IsFull() {
		return errors.New("queue full")
	}
	//分析出 this.tail 在队列尾部，但是包含最后的元素
	this.array[this.tail] = val // 把值给尾部
	this.tail = (this.tail + 1) % this.maxSize
	return
}

//出队列
func (this *CircleQueue) Pop() (val int, err error) {
	if this.IsEmpty() {
		return 0, errors.New("queue empty")
	}

	//取出,head 是指向队首，并且含队首元素
	val = this.array[this.head]
	this.head = (this.head + 1) % this.maxSize
	return
}

//显示队列
func (this *CircleQueue) ListQueue() {
	fmt.Println("环形队列情况如下：")
	//取出当前队列有多少个元素
	size := this.Size()
	if size == 0 {
		fmt.Println("队列为空")
	}
	//设计一个辅助的变量，指向 head
	tempHead := this.head
	for i := 0; i < size; i++ {
		fmt.Printf("arr[%d]=%d\t", tempHead, this.array[tempHead])
		tempHead = (tempHead + 1) % this.maxSize
	}
	fmt.Println()
}

//判断环形队列为满
func (this *CircleQueue) IsFull() bool {
	return (this.tail+1)%this.maxSize == this.head
}

//判断环形队列是空
func (this *CircleQueue) IsEmpty() bool {
	return this.tail == this.head
}

//取出环形队列有多少个元素
func (this *CircleQueue) Size() int {
	//这是一个关键的算法.
	return (this.tail + this.maxSize - this.head) % this.maxSize
}

//编写一个主函数测试，测试
func main() {
	//先创建一个队列
	queue := &CircleQueue{
		maxSize: 5, head: 0, tail: 0,
	}

	var key string
	var val int
	for {
		fmt.Println("1. 输入 add 表示添加数据到队列")
		fmt.Println("2. 输入 get 表示从队列获取数据")
		fmt.Println("3. 输入 show 表示显示队列")
		fmt.Println("4. 输入 exit 表示退出程序")

		fmt.Scanln(&key)
		switch key {
		case "add":
			fmt.Println("输入你要入队列数")
			fmt.Scanln(&val)
			err := queue.Push(val)
			if err != nil {
				fmt.Println(err.Error())
			} else {
				fmt.Println("加入队列ok")
			}
		case "get":
			val, err := queue.Pop()
			if err != nil {
				fmt.Println(err.Error())
			} else {
				fmt.Println("从队列中取出了一个数=", val)
			}
		case "show":
			queue.ListQueue()
		case "exit":
			os.Exit(0)
		}
	}
}

PS D:\Workspace\Go\src\projects\gin-demo> go run test.go
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
add
输入你要入队列数
1
加入队列ok
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
add
输入你要入队列数
4
加入队列ok
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
add
输入你要入队列数
7
加入队列ok
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
show
环形队列情况如下：
arr[0]=1        arr[1]=4        arr[2]=7
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
get
从队列中取出了一个数= 1
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
get
从队列中取出了一个数= 4
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
get
从队列中取出了一个数= 7
1. 输入 add 表示添加数据到队列
2. 输入 get 表示从队列获取数据
3. 输入 show 表示显示队列
4. 输入 exit 表示退出
exit

20.6 链表

20.6.3 单链表的应用实例

 案例的说明：

使用带 head 头的单向链表实现 –水浒英雄排行榜管理

完成对英雄人物的增删改查操作， 注 : 删除和修改 , 查找可以考虑学员独立完成

 第一种方法在添加英雄时，直接添加到链表的尾部

 代码实现：

package main

import "fmt"

//定义一个 HeroNode
type HeroNode struct {
	no       int
	name     string
	nickname string
	next     *HeroNode //这个表示指向下一个结点
}

//给链表插入一个结点
//编写第一种插入方法，在单链表的最后加入.[简单]
func InsertHreoNode(head *HeroNode, newHeroNode *HeroNode) {
	//思路
	//1. 先找到该链表的最后这个结点
	//2. 创建一个辅助结点[跑龙套, 帮忙]
	temp := head
	for {
		if temp.next == nil { //表示找到最后
			break
		}
		temp = temp.next // 让 temp 不断的指向下一个结点
	}

	//3. 将 newHeroNode 加入到链表的最后
	temp.next = newHeroNode
}

//给链表插入一个结点
//编写第 2 种插入方法，根据 no 的编号从小到大插入..【实用】
func InsertHreoNode2(head *HeroNode, newHeroNode *HeroNode) {
	//思路
	//1. 找到适当的结点
	//2. 创建一个辅助结点[跑龙套, 帮忙]
	temp := head
	flag := true
	//让插入的结点的 no，和 temp 的下一个结点的 no 比较
	for {
		if temp.next == nil { //说明到链表的最后
			break
		} else if temp.next.no >= newHeroNode.no {
			//说明 newHeroNode 就应该插入到 temp 后面
			break
		} else if temp.next.no == newHeroNode.no {
			//说明我们额链表中已经有这个 no,就不然插入.
			flag = false
			break
		}
		temp = temp.next
	}
	if !flag {
		fmt.Println("对不起，已经存在 no=", newHeroNode.no)
		return
	} else {
		newHeroNode.next = temp.next
		temp.next = newHeroNode
	}
}

//显示链表的所有结点信息
func ListHeroNode(head *HeroNode) {
	//1. 创建一个辅助结点[跑龙套, 帮忙]
	temp := head

	// 先判断该链表是不是一个空的链表
	if temp.next == nil {
		fmt.Println("空空如也")
		return
	}
	//2. 遍历这个链表
	for {
		fmt.Printf("[%d, %s, %s]==>", temp.next.no, temp.next.name, temp.next.nickname)
		// 判断是否是链表最后
		temp = temp.next
		if temp.next == nil {
			break
		}
	}
}

// 删除一个结点：
func DelHeroNode(head *HeroNode, id int) {
	temp := head
	flag := false
	// 找到要删除结点的no，和temp的下一个结点的no比较
	for {
		if temp.next == nil { // 说明到链表的最后
			break
		} else if temp.next.no == id {
			// 说明我们找到了
			flag = true
			break
		}
		temp = temp.next
	}
	if flag { // 找到，删除
		temp.next = temp.next.next
	} else {
		fmt.Println("sorry, 要删除的id不存在")
	}
}

func main() {
	//1. 先创建一个头结点
	head := &HeroNode{}

	//2. 创建一个新的 HeroNode
	hero1 := &HeroNode{
		no:       1,
		name:     "宋江",
		nickname: "及时雨",
	}

	hero2 := &HeroNode{
		no: 2, name: "卢俊义", nickname: "玉麒麟",
	}

	hero3 := &HeroNode{
		no: 3, name: "林冲", nickname: "豹子头",
	}

	hero4 := &HeroNode{
		no: 3, name: "吴用", nickname: "智多星",
	}

	//3. 加入
	InsertHreoNode2(head, hero3)
	InsertHreoNode2(head, hero1)
	InsertHreoNode2(head, hero2)
	InsertHreoNode2(head, hero4)

	// 4. 显示
	ListHeroNode(head)

}

PS D:\Workspace\Go\src\projects\gin-demo> go run test.go
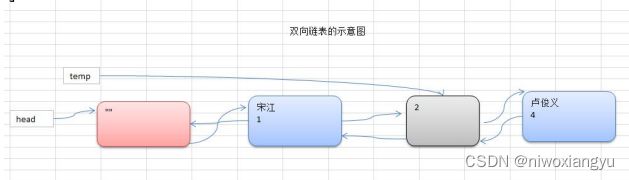
[1, 宋江, 及时雨]==>[2, 卢俊义, 玉麒麟]==>[3, 吴用, 智多星]==>[3, 林冲, 豹子头]==>

20.6.4 双向链表的应用实例

 示意图

代码实现

package main

import "fmt"

//定义一个 HeroNode
type HeroNode struct {
	no       int
	name     string
	nickname string
	pre      *HeroNode // 这个表示指向前一个结点
	next     *HeroNode // 这个表示指向下一个结点
}

//给双向链表插入一个结点
//编写第一种插入方法，在单链表的最后加入.[简单]
func InsertHreoNode(head *HeroNode, newHeroNode *HeroNode) {
	//思路
	//1. 先找到该链表的最后这个结点
	//2. 创建一个辅助结点[跑龙套, 帮忙]
	temp := head
	for {
		if temp.next == nil { //表示找到最后
			break
		}
		temp = temp.next // 让 temp 不断的指向下一个结点
	}

	//3. 将 newHeroNode 加入到链表的最后
	temp.next = newHeroNode
	newHeroNode.pre = temp
}

//给双向链表插入一个结点
//编写第 2 种插入方法，根据 no 的编号从小到大插入..【实用】
func InsertHreoNode2(head *HeroNode, newHeroNode *HeroNode) {
	//思路
	//1. 找到适当的结点
	//2. 创建一个辅助结点[跑龙套, 帮忙]
	temp := head
	flag := true
	//让插入的结点的 no，和 temp 的下一个结点的 no 比较
	for {
		if temp.next == nil { //说明到链表的最后
			break
		} else if temp.next.no >= newHeroNode.no {
			//说明 newHeroNode 就应该插入到 temp 后面
			break
		} else if temp.next.no == newHeroNode.no {
			//说明我们额链表中已经有这个 no,就不然插入.
			flag = false
			break
		}
		temp = temp.next
	}
	if !flag {
		fmt.Println("对不起，已经存在 no=", newHeroNode.no)
		return
	} else {
		newHeroNode.next = temp.next // ok
		newHeroNode.pre = temp       // ok
		if temp.next != nil {
			temp.next.pre = newHeroNode // ok
		}
		temp.next = newHeroNode // ok
	}
}

//显示链表的所有结点信息
//这里仍然使用单向的链表显示方式
func ListHeroNode(head *HeroNode) {
	//1. 创建一个辅助结点[跑龙套, 帮忙]
	temp := head

	// 先判断该链表是不是一个空的链表
	if temp.next == nil {
		fmt.Println("空空如也")
		return
	}
	//2. 遍历这个链表
	for {
		fmt.Printf("[%d, %s, %s]==>", temp.next.no, temp.next.name, temp.next.nickname)
		// 判断是否是链表最后
		temp = temp.next
		if temp.next == nil {
			break
		}
	}
}

func ListHeroNode2(head *HeroNode) {
	//1. 创建一个辅助结点[跑龙套, 帮忙]
	temp := head
	// 先判断该链表是不是一个空的链表
	if temp.next == nil {
		fmt.Println("空空如也。。。。")
		return
	}
	//2. 让 temp 定位到双向链表的最后结点
	for {
		if temp.next == nil {
			break
		}
		temp = temp.next
	}
	//2. 遍历这个链表
	for {
		fmt.Printf("[%d , %s , %s]==>", temp.no, temp.name, temp.nickname)
		//判断是否链表头
		temp = temp.pre
		if temp.pre == nil {
			break
		}
	}
}

// 删除一个结点：[双向链表删除一个结点]
func DelHeroNode(head *HeroNode, id int) {
	temp := head
	flag := false
	// 找到要删除结点的no，和temp的下一个结点的no比较
	for {
		if temp.next == nil { // 说明到链表的最后
			break
		} else if temp.next.no == id {
			// 说明我们找到了
			flag = true
			break
		}
		temp = temp.next
	}
	if flag { // 找到，删除
		temp.next = temp.next.next
		if temp.next != nil {
			temp.next.pre = temp
		}
	} else {
		fmt.Println("sorry, 要删除的id不存在")
	}
}

func main() {
	//1. 先创建一个头结点
	head := &HeroNode{}

	//2. 创建一个新的 HeroNode
	hero1 := &HeroNode{
		no:       1,
		name:     "宋江",
		nickname: "及时雨",
	}

	hero2 := &HeroNode{
		no: 2, name: "卢俊义", nickname: "玉麒麟",
	}

	hero3 := &HeroNode{
		no: 3, name: "林冲", nickname: "豹子头",
	}

	//3. 加入
	InsertHreoNode2(head, hero1)
	InsertHreoNode2(head, hero2)
	InsertHreoNode2(head, hero3)

	// 4. 显示
	ListHeroNode(head)
	fmt.Println()
	fmt.Println("逆序打印")
	ListHeroNode2(head)

}

PS D:\Workspace\Go\src\projects\gin-demo> go run test.go
[1, 宋江, 及时雨]==>[2, 卢俊义, 玉麒麟]==>[3, 林冲, 豹子头]==>
逆序打印
[3 , 林冲 , 豹子头]==>[2 , 卢俊义 , 玉麒麟]==>[1 , 宋江 , 及时雨]==>

20.6.5 单向环形链表的应用场景

20.6.6 环形单向链表介绍

20.6.7 环形的单向链表的案例

完成对单向环形链表的 添加结点 ， 删除结点 和 显示

package main

import "fmt"

//定义猫的结构体结点
type CatNode struct {
	no   int // 猫猫的编号
	name string
	next *CatNode
}

func InsertCatNode(head *CatNode, newCatNode *CatNode) {
	//判断是不是添加第一只猫
	if head.next == nil {
		head.no = newCatNode.no
		head.name = newCatNode.name
		head.next = head // 构成一个环形
		fmt.Println(newCatNode, "加入到环形的链表")
		return
	}

	//定义一个临时变量，帮忙,找到环形的最后结点
	temp := head
	for {
		if temp.next == head {
			break
		}
		temp = temp.next
	}
	//加入到链表中
	temp.next = newCatNode
	newCatNode.next = head
}

//输出这个环形的链表
func ListCircleLink(head *CatNode) {
	fmt.Println("环形链表的情况如下：")
	temp := head
	if temp.next == nil {
		fmt.Println("空空如也的环形链表...")
		return
	}
	for {
		fmt.Printf("猫的信息为为=[id=%d name=%s] ->\n", temp.no, temp.name)
		if temp.next == head {
			break
		}
		temp = temp.next
	}
}

//删除一只猫
func DelCatNode(head *CatNode, id int) *CatNode {
	temp := head
	helper := head
	//空链表
	if temp.next == nil {
		fmt.Println("这是一个空的环形链表，不能删除")
		return head
	}
	//如果只有一个结点
	if temp.next == head { //只有一个结点
		if temp.no == id {
			temp.next = nil
		}
		return head
	}

	//将 helper 定位到链表最后
	for {
		if helper.next == head {
			break
		}
		helper = helper.next

	}
	//如果有两个包含两个以上结点
	flag := true
	for {
		if temp.next == head { //如果到这来，说明我比较到最后一个【最后一个还没比较】
			break
		}
		if temp.no == id {
			if temp == head { //说明删除的是头结点
				head = head.next
			}
			//恭喜找到., 我们也可以在直接删除
			helper.next = temp.next
			fmt.Printf("猫猫猫=%d\n", id)
			flag = false
			break
		}
		temp = temp.next     // 移动 【比较】
		helper = helper.next // 移动 【一旦找到要删除的结点 helper】
	}
	//这里还有比较一次
	if flag { //如果 flag 为真，则我们上面没有删除
		if temp.no == id {
			helper.next = temp.next
			fmt.Printf("猫猫=%d\n", id)
		} else {
			fmt.Printf("对不起，没有 no=%d\n", id)
		}
	}
	return head
}

func main() {
	//这里我们初始化一个环形链表的头结点
	head := &CatNode{}
	//创建一只猫
	cat1 := &CatNode{
		no:   1,
		name: "tom",
	}
	cat2 := &CatNode{
		no: 2, name: "tom2",
	}
	cat3 := &CatNode{
		no: 3, name: "tom3",
	}
	InsertCatNode(head, cat1)
	InsertCatNode(head, cat2)
	InsertCatNode(head, cat3)
	ListCircleLink(head)

	head = DelCatNode(head, 30)

	fmt.Println()
	fmt.Println()
	fmt.Println()

	ListCircleLink(head)
}

PS D:\Workspace\Go\src\projects\gin-demo> go run test.go
&{1 tom } 加入到环形的链表
环形链表的情况如下：
猫的信息为为=[id=1 name=tom] ->
猫的信息为为=[id=2 name=tom2] ->
猫的信息为为=[id=3 name=tom3] ->
对不起，没有 no=30



环形链表的情况如下：
猫的信息为为=[id=1 name=tom] ->
猫的信息为为=[id=2 name=tom2] ->
猫的信息为为=[id=3 name=tom3] ->

20.6.8 环形单向链表的应用实例

 Josephu 问题

Josephu 问题为：设编号为 1 ， 2 ，… n 的 n 个人围坐一圈，约定编号为 k （ 1<=k<=n ）的人从 1

开始报数，数到 m 的那个人出列，它的下一位又从 1 开始报数，数到 m 的那个人又出列，依次类推，

直到所有人出列为止，由此产生一个出队编号的序列。

提示

用一个不带头结点的循环链表来处理 Josephu 问题：先构成一个有 n 个结点的单循环链表，然后

由 k 结点起从 1 开始计数，计到 m 时，对应结点从链表中删除，然后再从被删除结点的下一个结点又 从 1 开始计数，直到最后一个结点从链表中删除算法结束。

示意图说明

代码：

package main

import "fmt"

//小孩的结构体
type Boy struct {
	No   int  // 编号
	Next *Boy // 指向下一个小孩的指针[默认值是 nil]
}

// 编写一个函数，构成单向的环形链表
// num ：表示小孩的个数
// *Boy : 返回该环形的链表的第一个小孩的指针
func AddBoy(num int) *Boy {
	first := &Boy{}  // 空结点
	curBoy := &Boy{} // 空结点

	// 判断
	if num < 1 {
		fmt.Println("num 的值不对")
		return first
	}
	// 循环的构建这个环形链表
	for i := 1; i <= num; i++ {
		boy := &Boy{
			No: i,
		}
		//分析构成循环链表，需要一个辅助指针[帮忙的]
		//1. 因为第一个小孩比较特殊
		if i == 1 { //第一个小孩
			first = boy // 不要动
			curBoy = boy
			curBoy.Next = first
		} else {
			curBoy.Next = boy
			curBoy = boy
			curBoy.Next = first // /构造环形链表
		}
	}
	return first
}

//显示单向的环形链表[遍历]
func ShowBoy(first *Boy) {
	//处理一下如果环形链表为空
	if first.Next == nil {
		fmt.Println("链表为空，没有小孩...")
		return
	}
	//创建一个指针，帮助遍历.[说明至少有一个小孩]
	curBoy := first
	for {
		fmt.Printf("小孩编号=%d->", curBoy.No)
		// 退出的条件?curBoy.Next == first
		if curBoy.Next == first {
			break
		}
		//curBoy 移动到下一个
		curBoy = curBoy.Next
	}
}

/*
设编号为 1，2，… n 的 n 个人围坐一圈，约定编号为 k（1<=k<=n）
的人从 1 开始报数，数到 m 的那个人出列，它的下一位又从 1 开始报数，
数到 m 的那个人又出列，依次类推，直到所有人出列为止，由此产生一个出队编号的序列
*/

//分析思路
//1. 编写一个函数，PlayGame(first *Boy, startNo int, countNum int)
//2. 最后我们使用一个算法，按照要求，在环形链表中留下最后一个人
func PlayGame(first *Boy, startNo int, countNum int) {
	// 空的链表我们单独的处理
	if first.Next == nil {
		fmt.Println("空的链表，没有小孩")
		return
	}
	//留一个，判断 startNO <= 小孩的总数
	//2. 需要定义辅助指针，帮助我们删除小孩
	tail := first
	//3. 让 tail 执行环形链表的最后一个小孩,这个非常的重要
	//因为 tail 在删除小孩时需要使用到
	for {
		if tail.Next == first { //说明 tail 到了最后的小孩
			break
		}
		tail = tail.Next
	}
	//4. 让 first 移动到 startNo [后面我们删除小孩，就以 first 为准]
	for i := 1; i <= startNo-1; i++ {
		first = first.Next
		tail = tail.Next
	}
	fmt.Println()
	//5. 开始数 countNum, 然后就删除 first 指向的小孩
	for {
		//开始数 countNum-1 次
		for i := 1; i <= countNum-1; i++ {
			first = first.Next
			tail = tail.Next
		}
		fmt.Printf("小孩编号为%d 出圈 \n", first.No)
		//删除 first 指向的小孩
		first = first.Next
		tail = tail.Next
		//判断如果 tail == first, 圈子中只有一个小孩.
		if tail == first {
			break
		}
	}
	fmt.Printf("小孩小孩编号为%d 出圈 \n", first.No)
}

func main() {
	first := AddBoy(500)
	// 显示
	ShowBoy(first)
	PlayGame(first, 20, 31)
}

20.7 排序算法

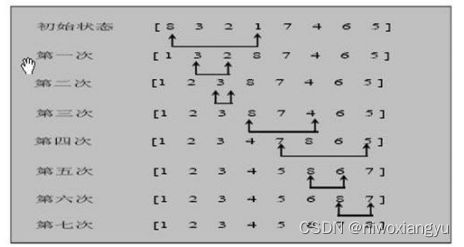
20.7.2 冒泡排序

20.7.3 选择排序基本介绍

选择排序（select sorting）也是一种简单的排序方法。它的基本思想是：第一次从 R[0]~R[n-1] 中选 取最小值，与 R[0] 交换，第二次从 R[1]~R[n-1] 中选取最小值，与 R[1] 交换，第三次从 R[2]~R[n-1] 中选 取最小值，与 R[2] 交换，…，第 i 次从 R[i-1]~R[n-1] 中选取最小值，与 R[i-1] 交换，… , 第 n-1 次从 R[n-2]~R[n-1]中选取最小值，与 R[n-2] 交换，总共通过 n-1 次，得到一个按排序码从小到大排列的有序序列

代码实现

func SelectSort(arr *[6]int) {
	// 标准的访问方式
	// (*arr)[1] = 600 等价于 arr[1] = 900
	// arr[1] = 900
	// 1.先完成将第一个最大值和arr[0]=>先易后难

	// 1 假设 arr[0]最大值
	for j := 0; j < len(arr)-1; j++ {
		max := arr[j]
		maxIndex := j
		// 2.遍历后面 1---[len(arr)-1]比较
		for i := j + 1; i < len(arr); i++ {
			if max < arr[i] { // 找到真正的最大值
				max = arr[i]
				maxIndex = i
			}
		}
		// 交换
		if maxIndex != j {
			arr[j], arr[maxIndex] = arr[maxIndex], arr[j]
		}
		fmt.Printf("第%d次 %v\n ", j+1, *arr)
	}
}

20.7.7 插入排序法介绍:

插入排序（Insertion Sorting）的基本思想是：把 n 个待排序的元素看成为一个有序表和一个无序表， 开始时有序表中只包含一个元素，无序表中包含有 n-1 个元素，排序过程中每次从无序表中取出第一个 元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的适当位置，使之成 为新的有序表。

20.7.10 插入排序法应用实例

20.7.11 插入排序的代码实现

package main

import (
	"fmt"
)

func InsertSort(arr *[7]int) {
	// 完成第一次，给第二个元素找到合适的位置并插入
	for i := 1; i < len(arr); i++ {
		insertVal := arr[i]
		insertIndex := i - 1 // 下标

		// 从大到小
		for insertIndex >= 0 && arr[insertIndex] < insertVal {
			arr[insertIndex+1] = arr[insertIndex] // 数据后移
			insertIndex--
		}
		// 插入
		if insertIndex+1 != i {
			// 插入到insertIndex + 1这个位置
			arr[insertIndex+1] = insertVal
		}
		fmt.Printf("第%d次插入后 %v\n", i, *arr)
	}
}

func main() {
	array1 := [7]int{23, 0, 12, 56, 34}
	InsertSort(&array1)
}

PS D:\Workspace\Go\src\projects\testorm> go run main.go
第1次插入后 [23 0 12 56 34]
第2次插入后 [23 12 0 56 34]
第3次插入后 [56 23 12 0 34]
第4次插入后 [56 34 23 12 0]

20.7.12 快速排序法介绍

快速排序（ Quicksort ）是对冒泡排序的一种改进。基本思想是：通过一趟排序将要排序的数据分

割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列.

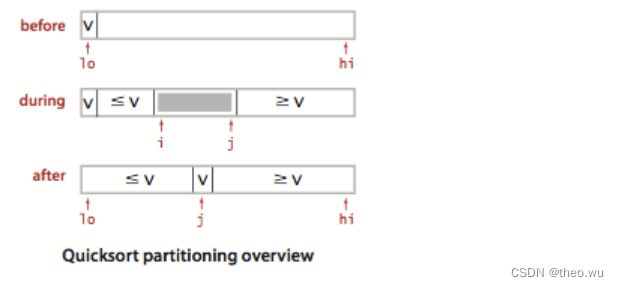
20.7.13 快速排序法示意图

 20.7.14 快速排序法应用实例

20.7.15 快速排序法的代码实现

package main

import (
	"fmt"
)

//快速排序
//说明
//1. left 表示 数组左边的下标
//2. right 表示数组右边的下标
//3 array 表示要排序的数组
func QuickSort(left int, right int, array *[9]int) {
	l := left
	r := right
	// pivot 是中轴， 支点
	pivot := array[(left+right)/2]
	temp := 0
	//for 循环的目标是将比 pivot 小的数放到 左边
	// 比 pivot 大的数放到 右边
	for l < r {
		//从 pivot 的左边找到大于等于 pivot 的值
		for array[l] < pivot {
			l++
		}
		//从 pivot 的右边边找到小于等于 pivot 的值
		for array[r] > pivot {
			r--
		}
		// 1 >= r 表明本次分解任务完成, break
		if l >= r {
			break
		}
		//交换
		temp = array[l]
		array[l] = array[r]
		array[r] = temp
		//优化
		if array[l] == pivot {
			r--
		}
		if array[r] == pivot {
			l++
		}
	}
	// 如果 1== r, 再移动下
	if l == r {
		l++
		r--
	}
	// 向左递归
	if left < r {
		QuickSort(left, r, array)
	}
	// 向右递归
	if right > l {
		QuickSort(l, right, array)
	}
}

func main() {
	arr := [9]int{-9, 78, 0, 23, -567, 70, 123, 90, -23}
	fmt.Println("初始", arr)
	//调用快速排序
	QuickSort(0, len(arr)-1, &arr)
	fmt.Println("main..")
	fmt.Println(arr)
}

PS D:\Workspace\Go\src\projects\testorm> go run main.go
初始 [-9 78 0 23 -567 70 123 90 -23]
main..
[-567 -23 -9 0 23 70 78 90 123]

20.8 栈

20.8.1 看一个实际需求

 20.8.3 栈的入栈和出栈的示意图

 20.8.4 栈的应用场景

1) 子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再

将地址取出，以回到原来的程序中。

2) 处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外，也将参数、区域变

量等数据存入堆栈中。

3) 表达式的转换与求值。

4) 二叉树的遍历。

5) 图形的深度优先 (depth 一 first) 搜索法。

20.8.5 栈的案例

 代码实现

package main

import (
	"errors"
	"fmt"
)

// 使用数组来模拟一个栈的使用
type Stack struct {
	MaxTop int    // 表示我们栈最大可以存放数个数
	Top    int    // 表示栈顶，因为栈顶固定，因此我们直接使用Top
	arr    [5]int // 数组模拟栈
}

// 入栈
func (this *Stack) Push(val int) (err error) {
	// 先判断栈是否满了
	if this.Top == this.MaxTop-1 {
		fmt.Println("stack full")
		return errors.New("stack full")
	}
	this.Top++
	// 放入数据
	this.arr[this.Top] = val
	return
}

// 出栈
func (this *Stack) Pop() (val int, err error) {
	// 判断栈是否为空
	if this.Top == -1 {
		fmt.Println("stack empty!")
		return 0, errors.New("stack empty")
	}

	// 先取值，再this.Top--
	val = this.arr[this.Top]
	this.Top--
	return val, nil
}

// 遍历栈，注意需要从栈顶开始遍历
func (this *Stack) List() {
	// 先判断栈是否为空
	if this.Top == -1 {
		fmt.Println("stack empty")
		return
	}
	fmt.Println("栈的情况如下：")
	for i := this.Top; i >= 0; i-- {
		fmt.Printf("arr[%d]%d\n", i, this.arr[i])
	}
}

20.8.6 栈实现综合计算器

 分析了实现的思路

 代码实现

package main

import (
	"errors"
	"fmt"
	"strconv"
)

// 使用数组来模拟一个栈的使用
type Stack struct {
	MaxTop int    // 表示我们栈最大可以存放数个数
	Top    int    // 表示栈顶，因为栈顶固定，因此我们直接使用Top
	arr    [5]int // 数组模拟栈
}

// 入栈
func (this *Stack) Push(val int) (err error) {
	// 先判断栈是否满了
	if this.Top == this.MaxTop-1 {
		fmt.Println("stack full")
		return errors.New("stack full")
	}
	this.Top++
	// 放入数据
	this.arr[this.Top] = val
	return
}

// 出栈
func (this *Stack) Pop() (val int, err error) {
	// 判断栈是否为空
	if this.Top == -1 {
		fmt.Println("stack empty!")
		return 0, errors.New("stack empty")
	}

	// 先取值，再this.Top--
	val = this.arr[this.Top]
	this.Top--
	return val, nil
}

// 遍历栈，注意需要从栈顶开始遍历
func (this *Stack) List() {
	// 先判断栈是否为空
	if this.Top == -1 {
		fmt.Println("stack empty")
		return
	}
	fmt.Println("栈的情况如下：")
	for i := this.Top; i >= 0; i-- {
		fmt.Printf("arr[%d]%d\n", i, this.arr[i])
	}
}

//判断一个字符是不是一个运算符[+, - , * , /]
func (this *Stack) IsOper(val int) bool {
	if val == 42 || val == 43 || val == 45 || val == 47 {
		return true
	} else {
		return false
	}
}

//运算的方法
func (this *Stack) Cal(num1 int, num2 int, oper int) int {
	res := 0
	switch oper {
	case 42:
		res = num2 * num1
	case 43:
		res = num2 + num1
	case 45:
		res = num2 - num1
	case 47:
		res = num2 / num1
	default:
		fmt.Println("运算符错误.")
	}
	return res
}

//编写一个方法，返回某个运算符的优先级[程序员定义]
//[* / => 1 + - => 0]
func (this *Stack) Priority(oper int) int {
	res := 0
	if oper == 42 || oper == 47 {
		res = 1
	} else if oper == 43 || oper == 45 {
		res = 0
	}
	return res
}

func main() {
	//数栈
	numStack := &Stack{
		MaxTop: 20,
		Top:    -1,
	}
	//符号栈
	operStack := &Stack{
		MaxTop: 20,
		Top:    -1,
	}

	exp := "30+30*6-4-6"
	//定义一个 index ，帮助扫描 exp
	index := 0
	//为了配合运算，我们定义需要的变量
	num1 := 0
	num2 := 0
	oper := 0
	result := 0
	keepNum := ""

	for {
		//这里我们需要增加一个逻辑，
		//处理多位数的问题
		ch := exp[index : index+1] // 字符串
		//ch ==>"+" ===> 43
		temp := int([]byte(ch)[0])  // 就是字符对应的 ASCiI 码
		if operStack.IsOper(temp) { // 说明是符号
			//如果 operStack 是一个空栈， 直接入栈
			if operStack.Top == -1 { //空栈
				operStack.Push(temp)
			} else {
				//如果发现 opertStack 栈顶的运算符的优先级大于等于当前准备入栈的运算符的优先级
				//，就从符号栈 pop 出，并从数栈也 pop 两个数，进行运算，运算后的结果再重新入栈
				//到数栈， 当前符号再入符号栈
				if operStack.Priority(operStack.arr[operStack.Top]) >=
					operStack.Priority(temp) {
					num1, _ := numStack.Pop()
					num2, _ := numStack.Pop()
					oper, _ := operStack.Pop()
					result = operStack.Cal(num1, num2, oper)
					//将计算结果重新入数栈
					numStack.Push(result)
					//当前的符号压入符号栈
					operStack.Push(temp)
				} else {
					operStack.Push(temp)
				}
			}
		} else { //说明是数
			//处理多位数的思路
			//1.定义一个变量 keepNum string, 做拼接
			keepNum += ch
			//2.每次要向 index 的后面字符测试一下，看看是不是运算符，然后处理
			//如果已经到表达最后，直接将 keepNum
			if index == len(exp)-1 {
				val, _ := strconv.ParseInt(keepNum, 10, 64)
				numStack.Push(int(val))
			} else {
				//向 index 后面测试看看是不是运算符 [index]
				if operStack.IsOper(int([]byte(exp[index+1 : index+2])[0])) {
					val, _ := strconv.ParseInt(keepNum, 10, 64)
					numStack.Push(int(val))
					keepNum = ""
				}
			}
		}
		//继续扫描
		//先判断 index 是否已经扫描到计算表达式的最后
		if index+1 == len(exp) {
			break
		}
		index++
	}
	//如果扫描表达式 完毕，依次从符号栈取出符号，然后从数栈取出两个数，
	//运算后的结果，入数栈，直到符号栈为空
	for {
		if operStack.Top == -1 {
			break // 退出条件
		}
		num1, _ = numStack.Pop()
		num2, _ = numStack.Pop()
		oper, _ = operStack.Pop()
		result = operStack.Cal(num1, num2, oper)
		//将计算结果重新入数栈
		numStack.Push(result)
	}
	//如果我们的算法没有问题，表达式也是正确的，则结果就是 numStack 最后数
	res, _ := numStack.Pop()
	fmt.Printf("表达式%s = %v", exp, res)
}

PS D:\Workspace\Go\src\projects\testorm> go run main.go
表达式30+30*6-4-6 = 200

20.9 递归

20.9.1 递归的一个应用场景[迷宫问题]

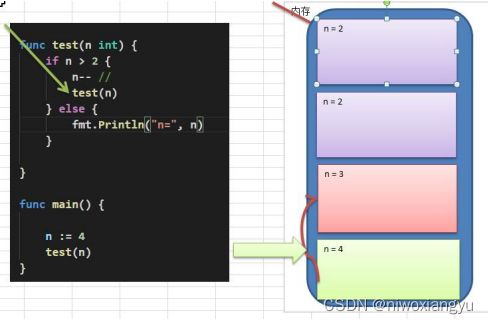
 20.9.2 递归的概念

简单的说 : 第归就是函数 / 方法 自己调用自己 , 每次调用时传入不同的变量 . 第归有助于编程者解决

复杂的问题 , 同时可以让代码变得简洁。

20.9.3 递归快速入门

1) 打印问题

2) 阶乘问题

3) 快速入门的示意图

20.9.4 递归用于解决什么样的问题

1 ） 各种数学问题如 : 8 皇后问题 , 汉诺塔 , 阶乘问题 , 迷宫问题 , 球和篮子的问题 (google 编程大

赛 )

2 ） 将用栈解决的问题 --> 第归代码比较简洁

20.9.5 递归需要遵守的重要原则

1) 执行一个函数时，就创建一个新的受保护的 独立空间 ( 新函数栈 )

2) 函数的局部变量是独立的，不会相互影响 , 如果希望各个函数栈使用同一个数据，使用引用传递

3) 递归必须向 退出递归的条件逼近【程序员自己必须分析】 ，否则就是无限递归，死龟了 :)

4) 当一个函数执行完毕，或者遇到 return，就会返回，遵守谁调用，就将结果返回给谁，同时当函数执行完毕或者返回时，该函数本身也会被系统销毁

20.9.6 举一个比较综合的案例,迷宫问题

 代码

package main

import "fmt"

//编写一个函数，完成老鼠找路
//myMap *[8][7]int:地图，保证是同一个地图，使用引用
//i,j 表示对地图的哪个点进行测试
func SetWay(myMap *[8][7]int, i int, j int) bool {
	//分析出什么情况下，就找到出路
	//myMap[6][5] == 2
	if myMap[6][5] == 2 {
		return true
	} else {
		//说明要继续找
		if myMap[i][j] == 0 { //如果这个点是可以探测
			//假设这个点是可以通, 但是需要探测 上下左右
			//换一个策略 下右上左
			myMap[i][j] = 2
			if SetWay(myMap, i+1, j) { // 下
				return true
			} else if SetWay(myMap, i, j+1) { // 右
				return true
			} else if SetWay(myMap, i-1, j) { // 上
				return true
			} else if SetWay(myMap, i, j-1) { // 左
				return true
			} else { // 死路
				myMap[i][j] = 3
				return false
			}

		} else { // 说明这个点不能探测，为 1，是墙
			return false
		}
	}
}

func main() {
	//先创建一个二维数组，模拟迷宫
	//规则
	//1. 如果元素的值为 1 ，就是墙
	//2. 如果元素的值为 0, 是没有走过的点
	//3. 如果元素的值为 2, 是一个通路
	//4. 如果元素的值为 3， 是走过的点，但是走不通
	var myMap [8][7]int

	//先把地图的最上和最下设置为 1
	for i := 0; i < 7; i++ {
		myMap[0][i] = 1
		myMap[7][i] = 1
	}
	//先把地图的最左和最右设置为 1
	for i := 0; i < 8; i++ {
		myMap[i][0] = 1
		myMap[i][6] = 1
	}
	myMap[3][1] = 1
	myMap[3][2] = 1
	myMap[1][2] = 1
	myMap[2][2] = 1
	//输出地图
	for i := 0; i < 8; i++ {
		for j := 0; j < 7; j++ {
			fmt.Print(myMap[i][j], "")
		}
		fmt.Println()
	}
	//使用测试
	SetWay(&myMap, 1, 1)
	fmt.Println("探测完毕....")
	//输出地图
	for i := 0; i < 8; i++ {
		for j := 0; j < 7; j++ {
			fmt.Print(myMap[i][j], "")
		}
		fmt.Println()
	}
}

PS D:\Workspace\Go\src\projects\testorm> go run main.go
1111111
1010001
1010001
1110001
1000001
1000001
1000001
1111111
探测完毕....
1111111
1310001
1310001
1110001
1000001
1000001
1000001
1111111

课后思考题：

思考 : 如何求出最短路径 ?

20.10 哈希表(散列)

20.10.1 实际的需求

google 公司的一个上机题 :

有一个公司 , 当有新的员工来报道时 , 要求将该员工的信息加入 (id, 性别 , 年龄 , 住址 ..), 当输入该员工

的 id 时 , 要求查找到该员工的 所有信息 .

要求 : 不使用数据库 , 尽量节省内存 , 速度越快越好 => 哈希表 ( 散列 )

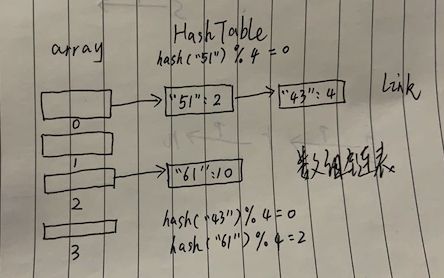
20.10.2 哈希表的基本介绍

散列表（ Hash table ，也叫哈希表），是根据关键码值 (Key value) 而直接进行访问的数据结构。也

就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做 散列函数，存放记录的数组叫做散列表。

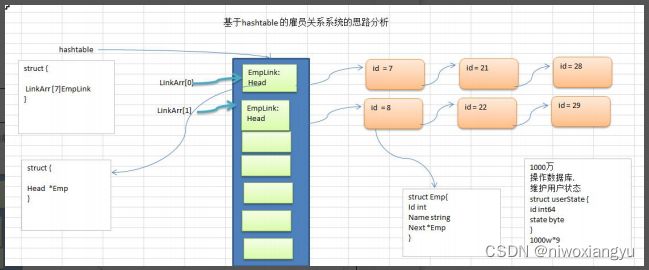
20.10.3 使用 hashtable 来实现一个雇员的管理系统[增删改查]

 应用实例 google 公司的一个上机题 :

有一个公司 , 当有新的员工来报道时 , 要求将该员工的信息加入 (id, 性别 , 年龄 , 住址 ..), 当输入该员工

的 id 时 , 要求查找到该员工的 所有信息 .

 要求 :

1) 不使用数据库 , 尽量节省内存 , 速度越快越好 => 哈希表 ( 散列 )

2) 添加时，保证按照雇员的 id 从低到高插入

 思路分析

1) 使用链表来实现哈希表 , 该 链表不带 表头

[ 即 : 链表的第一个结点就存放雇员信息 ]

2) 思路分析并画出示意图

3) 代码实现[增删改查(显示所有员工，按 id 查询)]

package main

import "fmt"

//定义 emp
type Emp struct {
	Id   int
	Name string
	Next *Emp
}

//定义 EmpLink
//我们这里的 EmpLink 不带表头,即第一个结点就存放雇员
type EmpLink struct {
	Head *Emp
}

//1. 添加员工的方法, 保证添加时，编号从小到大
func (this *EmpLink) Insert(emp *Emp) {
	cur := this.Head   // 这是辅助指针
	var pre *Emp = nil // 这是一个辅助指针 p
	//如果当前的 EmpLink 就是一个空链表
	if cur == nil {
		this.Head = emp // 完成
		return
	}
	//如果不是一个空链表,给 emp 找到对应的位置并插入
	//思路是 让 cur 和 emp 比较，然后让 pre 保持在 cur 前面
	for {
		if cur != nil {
			//比较
			if cur.Id > emp.Id {
				//找到位置
				break
			}
			pre = cur // 保证同步
			cur = cur.Next
		} else {
			break
		}
	}
	//退出时，我们看下是否将 emp 添加到链表最后
	pre.Next = emp
	emp.Next = cur
}

//显示链表的信息
func (this *EmpLink) ShowLink(no int) {
	if this.Head == nil {
		fmt.Printf("链表%d 为空\n", no)
		return
	}
	//变量当前的链表，并显示数据
	cur := this.Head // 辅助的指针
	for {
		if cur != nil {
			fmt.Printf("链表%d 雇员 id=%d 名字=%s ->", no, cur.Id, cur.Name)
			cur = cur.Next
		} else {
			break
		}
	}
	fmt.Println() //换行处理
}

//定义 hashtable ,含有一个链表数组
type HashTable struct {
	LinkArr [7]EmpLink
}

//给 HashTable 编写 Insert 雇员的方法
func (this *HashTable) Insert(emp *Emp) {
	//使用散列函数，确定将该雇员添加到哪个链表
	linkNo := this.HashFun(emp.Id)
	//使用对应的链表添加
	this.LinkArr[linkNo].Insert(emp)
}

//编写方法，显示 hashtable 的所有雇员
func (this *HashTable) ShowAll() {
	for i := 0; i < len(this.LinkArr); i++ {
		this.LinkArr[i].ShowLink(i)
	}
}

//编写一个散列方法
func (this *HashTable) HashFun(id int) int {
	return id % 7 //得到一个值，就是对于的链表的下标
}

func main() {
	key := ""
	id := 0
	name := ""
	var hashtable HashTable
	for {
		fmt.Println("===============雇员系统菜单============")
		fmt.Println("input 表示添加雇员")
		fmt.Println("show 表示显示雇员")
		fmt.Println("find 表示查找雇员")
		fmt.Println("exit 表示退出系统")
		fmt.Println("请输入你的选择")
		fmt.Scanln(&key)
		switch key {
		case "input":
			fmt.Println("输入雇员 id")
			fmt.Scanln(&id)
			fmt.Println("输入雇员 name")
			fmt.Scanln(&name)
			emp := &Emp{
				Id:   id,
				Name: name,
			}
			hashtable.Insert(emp)
		case "show":
			hashtable.ShowAll()
		case "exit":
            os.Exit(-1)
		default:
			fmt.Println("输入错误")
		}
	}
}

PS D:\Workspace\Go\src\projects\testorm> go run main.go
===============雇员系统菜单============
input 表示添加雇员
show 表示显示雇员
find 表示查找雇员
exit 表示退出系统
请输入你的选择
input
输入雇员 id
1
输入雇员 name
wu
===============雇员系统菜单============
input 表示添加雇员
show 表示显示雇员
find 表示查找雇员
exit 表示退出系统
请输入你的选择
input
输入雇员 id
2
输入雇员 name
ku
===============雇员系统菜单============
input 表示添加雇员
show 表示显示雇员
find 表示查找雇员
exit 表示退出系统
请输入你的选择
input
输入雇员 id
3
输入雇员 name
lu
===============雇员系统菜单============
input 表示添加雇员
show 表示显示雇员
find 表示查找雇员
exit 表示退出系统
请输入你的选择
show
链表0 为空
链表1 雇员 id=1 名字=wu ->
链表2 雇员 id=2 名字=ku ->
链表3 雇员 id=3 名字=lu ->
链表4 为空
链表5 为空
链表6 为空

数据结构和算法（Golang实现）

基础知识

一、什么是算法

汉诺塔问题可以描述为：

有三根杆 ( 编号 A 、 B 、 C ) ，在 A 杆自下而上、由大到小按顺序放置 64 个金盘 ( 如下

图 ) 。游戏的目标：把 A 杆上的金盘全部移到 C 杆上，并仍保持原有顺序叠好。

操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作

过程中盘子可以置于 A 、 B 、 C 任一杆上。

我们很自然想到一个算法：

1. 我们必须先借助 C 杆，将 A 杆前面 N-1 个盘子，移动到 B 杆后，将 A 杆剩下

的一个盘子，直接移动到 C 杆，这时候 A 空了。

2. 然后借助 A 杆，将 B 杆的 N-1 个盘子，移动到 C 杆，任务就完成了。

十分朴素的思路，我们用编程语言来实现：

package main

import "fmt"

var total = 0

// 汉诺塔
// 一开始A杆上有N个盘子，B和C杆都没有盘子。
func main() {
	n := 4   // 64 个盘子
	a := "a" // 杆子A
	b := "b" // 杆子B
	c := "c" // 杆子C
	tower(n, a, b, c)

	// 当 n=1 时，移动次数为 1
	// 当 n=2 时，移动次数为 3
	// 当 n=3 时，移动次数为 7
	// 当 n=4 时，移动次数为 15
	fmt.Println(total)
}

// 表示将N个盘子，从 a 杆，借助 b 杆移到 c 杆
func tower(n int, a, b, c string) {
	if n == 1 {
		total = total + 1
		fmt.Println(a, "->", c)
		return
	}

	tower(n-1, a, c, b)
	total = total + 1
	fmt.Println(a, "->", c)
	tower(n-1, b, a, c)
}

PS D:\Workspace\Go\src\projects\demo> go run main.go
a -> b
a -> c
b -> c
a -> b
c -> a
c -> b
a -> b
a -> c
b -> c
b -> a
c -> a
b -> c
a -> b
a -> c
b -> c
15

通过归纳，我们可以知道移动次数 Total(N) 的关系是 Total(N)=2*Total(N-1)+1 ，每多一

个盘子，移动次数就会翻倍加一，我们通过相关的数列数学方法可以知道 Total(N)=2^N-1 ，也就

是移动次数是一个指数方程 : 2 的 N 次方 , 指数等于盘子的数量。

我们计算出 2^64-1=18446744073709551615 ，可以知道一个人日夜不停，一秒移动一

次： 18446744073709551615/3600/24/365/100000000=5849 ，要 5849 亿年时间才可以完成这件

事，那时候世界确实可能已经毁灭。

在计算机科学中，因为所有的算法都是人定义的规则，规则是死的，所以不要担心学不会。当你学会了

这些算法，你将会觉得，哇，一切都那么简单。

二、什么是数据结构

数据结构，顾名思义就是存放数据的结构，也可以认为是存放数据的容器。比如，你要找出 1000 个数字 中的最大值，首先你要将1000 个数字记在某些卡片上，然后对卡片进行排序。

大多数算法都需要组织数据，所以产生了数据结构。数据结构在计算机中，主要是用来实现各种算法的 基础，当然数据结构本身也是算法的一部分。

基本的数据结构有：链表，栈和队列，树和图。

链表，就是把数据链接起来，关联起来，一个数据节点指向另外一个数据节点，像自然界的一条条铁链，大部分

数据结构，都是由链表的若干变种来表示。

在每种编程语言中，数组作为基本数据类型提供，数组是连续的内存存储空间，通过下标 0 ， 1 ， 2 可以迅速获取

到数组指定位置的数据。链表也可以用数组来实现，但一般情况下，因为数组是连续的，在链表增加和删除节点

时容易造成冗余，效果不佳。所以链表在不同编程语言实现是这样的： C 、 C++ 是用指针来实现

的， Java 是用类来实现的，而 Golang 是用结构体引用来实现。

栈和队列，主要用来存储多个数据，只不过一个是先进后出，一个先进先出。比如下压栈，先入栈的数据是最后

才能出来，而我们熟知的队列，先排队的人肯定先获得服务。

其次是树和图，树就是有一个树根节点，存放着数据，下面有很多子节点，也存放着数据，类比自然界的树。图

则可以类比自然界的地图，多个点指向多个点，点和点之间有一条或多条边，而这些点存放着数据，边也可以存

放着数据，比如距离等。

围绕这几种数据结构，有若干延伸，加上一些排序，查找逻辑，就形成了更高层次的高级数据结构。

数据结构是算法实现的辅助，是为了更高效组织数据的结构，所以数据结构和算法其实密切联系，并不需要分得太清，大家可以把数据结构等同于算法。

三、什么叫好的数据结构和好的算法

学习算法的原因，是好的算法可以节约资源，但是选择合适的算法很难。我们要进行复杂的数学分析才能知道，什么叫做好的，在计算机里，我们把这种数学分析这叫做算法分析。

什么是好的数据结构和好的算法？

1. 计算机资源是有限 的，所以占用计算机资源越少的数据结构和算法越好。

2. 人的生命是有限的 的，等待时间是有忍耐度的，所以能辅助程序越快完成工作的数据结构和算法越好。

所以出了个理论：时间和空间算法复杂度理论。

程序执行过程中，要么空间换时间，要么时间换空间，空间可以认为是一种计算机资源如内存使用情 况，而时间是人类感知的第四个维度，就是慢还是快，两者一般不能兼得，如果发现居然兼得了，那就 是发明了一种更好的算法。

在计算机科学发展的四五十年，这种既省资源又省时间的发明还是比较少的，比如数据压缩算法，因为发明了超高效的无损数据压缩算法，我们网上看视频的时候，既不失真，也不卡顿，又快又好，这种就叫好算法。

目前有一种新型的计算方式正在研究中，叫量子计算，可以在非常小的空间，使用非常少的资源，短时间内计算超级大量的数据，让我们期待能成功量产的那天，到了那时候，人类生产力将极大被解放。

四、总结

程序设计在一般程度上，很多人都认为 = 数据结构 + 算法。

我们学习数据结构和算法，是为了更高效率写出更快，更好的代码。

因为学习过，所以我们不需要从零开始设计，工作效率就提高了。

因为知道每种数据结构和算法的复杂度和适用场景，自由选择组合，我们写出的代码计算速度变快了，占用的资源更少了。

所以我们要好好学习和理解常见的数据结构和算法。

分治法和递归

在计算机科学中，分治法是一种很重要的算法。

字面上的解释是 分而治之 ，就是把一个复杂的问题分成两个或更多的相同或相似的子问题。

直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

分治法一般使用递归来求问题的解。

一、递归

递归就是不断地调用函数本身。

比如我们求阶乘 1 * 2 * 3 * 4 * 5 *...* N ：

package main

import "fmt"

func Rescuvie(n int) int {
	if n == 0 {
		return 1
	}
	return n * Rescuvie(n-1)
}
func main() {
	fmt.Println(Rescuvie(5))
}

会反复进入一个函数，它的过程如下 :

Rescuvie(5)
{5 * Rescuvie(4)}
{5 * {4 * Rescuvie(3)}}
{5 * {4 * {3 * Rescuvie(2)}}}
{5 * {4 * {3 * {2 * Rescuvie(1)}}}}
{5 * {4 * {3 * {2 * 1}}}}
{5 * {4 * {3 * 2}}}
{5 * {4 * 6}}
{5 * 24}
120

函数不断地调用本身，并且还乘以一个变量：n * Rescuvie(n-1)，这是一个递归的过程。

很容易看出, 因为递归式使用了运算符，每次重复的调用都使得运算的链条不断加长，系统不得不使用栈进行数据保存和恢复。

如果每次递归都要对越来越长的链进行运算，那速度极慢，并且可能栈溢出，导致程序奔溃。

所以有另外一种写法，叫尾递归：

package main

import "fmt"

func RescuvieTail(n int, a int) int {
	if n == 1 {
		return a
	}
	return RescuvieTail(n-1, a*n)
}
func main() {
	fmt.Println(RescuvieTail(5, 1))
}

他的递归过程如下 :

RescuvieTail(5, 1)
RescuvieTail(4, 1*5)=RescuvieTail(4, 5)
RescuvieTail(3, 5*4)=RescuvieTail(3, 20)
RescuvieTail(2, 20*3)=RescuvieTail(2, 60)
RescuvieTail(1, 60*2)=RescuvieTail(1, 120)
120

尾部递归是指递归函数在调用自身后直接传回其值，而不对其再加运算，效率将会极大的提高。

如果一个函数中所有递归形式的调用都出现在函数的末尾，我们称这个递归函数是尾递归的。当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时，这个递归调用就是尾递归。

尾递归函数的特点是在回归过程中不用做任何操作，这个特性很重要，因为大多数现代的编译器会利用 这种特点自动生成优化的代码。— 来自百度百科。

尾递归函数，部分高级语言编译器会进行优化，减少不必要的堆栈生成，使得程序栈维持固定的层数，不会出现栈溢出的情况。

我们将会举多个例子说明。

二、例子：斐波那契数列

斐波那契数列是指，后一个数是前两个数的和的一种数列。如下：

1 1 2 3 5 8 13 21 ... N-1 N 2N-1

尾递归的求解为：

package main

import "fmt"

func F(n int, a1, a2 int) int {
	if n == 0 {
		return a1
	}
	return F(n-1, a2, a1+a2)
}
func main() {
	fmt.Println(F(1, 1, 1))
	fmt.Println(F(2, 1, 1))
	fmt.Println(F(3, 1, 1))
	fmt.Println(F(4, 1, 1))
	fmt.Println(F(5, 1, 1))
}

输出：

1
2
3
5
8

当 n=5 的递归过程如下:

F(5,1,1)
F(4,1,1+1)=F(4,1,2)
F(3,2,1+2)=F(3,2,3)
F(2,3,2+3)=F(2,3,5)
F(1,5,3+5)=F(1,5,8)
F(0,8,5+8)=F(0,8,13)
8

三、例子：二分查找

在一个已经排好序的数列，找出某个数，如：

1 5 9 15 81 89 123 189 333

从上面排好序的数列中找出数字 189。

二分查找的思路是，先拿排好序数列的中位数与目标数字 189 对比，如果刚好匹配目标，结束。

如果中位数比目标数字大，因为已经排好序，所以中位数右边的数字绝对都比目标数字大，那么从中位数的左边找。

如果中位数比目标数字小，因为已经排好序，所以中位数左边的数字绝对都比目标数字小，那么从中位数的右边找。

这种分而治之，一分为二的查找叫做二分查找算法。

递归解法：

package main

import "fmt"

// 二分查找递归解法
func BinarySearch(array []int, target int, l, r int) int {
	if l > r {
		// 出界了，找不到
		return -1
	}
	//
	mid := (l + r) / 2
	middleNum := array[mid]

	if middleNum == target {
		return mid // 找到了
	} else if middleNum > target {
		// 中间的数比目标还大，从左边找
		return BinarySearch(array, target, 0, mid-1)
	} else {
		// 中间的数比目标还小，从右边找
		return BinarySearch(array, target, mid+1, r)
	}
}
func main() {
	array := []int{1, 5, 9, 15, 81, 89, 123, 189, 333}
	target := 500
	result := BinarySearch(array, target, 0, len(array)-1)
	fmt.Println(target, result)

	target = 189
	result = BinarySearch(array, target, 0, len(array)-1)
	fmt.Println(target, result)
}

输出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
500 -1
189 7

可以看到，189 这个数字在数列的下标 7 处，而 500 这个数找不到。

当然，递归解法都可以转化为非递归，如：

package main

import "fmt"

// 二分查找非递归解法
func BinarySearch2(array []int, target int, l, r int) int {
	ltemp := l
	rtemp := r

	for {
		if ltemp > rtemp {
			// 出界了，找不到
			return -1
		}
		// 从中间开始找
		mid := (ltemp + rtemp) / 2
		middleNum := array[mid]

		if middleNum == target {
			return mid // 找到了
		} else if middleNum > target {
			// 中间的数比目标还大，从左边找
			rtemp = mid - 1
		} else {
			// 中间的数比目标还小，从右边找
			ltemp = mid + 1
		}
	}
}
func main() {
	array := []int{1, 5, 9, 15, 81, 89, 123, 189, 333}
	target := 500
	result := BinarySearch2(array, target, 0, len(array)-1)
	fmt.Println(target, result)

	target = 189
	result = BinarySearch2(array, target, 0, len(array)-1)
	fmt.Println(target, result)
}

很多计算机问题都可以用递归来简化求解，理论上，所有的递归方式都可以转化为非递归的方式，只不过使用递归，代码的可读性更高。

算法复杂度及渐进符号

一、算法复杂度

首先每个程序运行过程中，都要占用一定的计算机资源，比如内存，磁盘等，这些是空间，计算过程中需要判断，循环执行某些逻辑，周而反复，这些是时间。

那么一个算法有多好，多快，怎么衡量一个算法的好坏？所以，计算机科学在算法分析过程中，提出了算法复杂度理论，这套理论可以量化算法的效率，以此作为标准，方便我们能衡量到底选择哪一种算法。

复杂度有两个维度：时间和空间。

我们说，一个实现了某算法的程序：

1. 如果计算的速度越快，那么这个算法时间复杂度越低。
2. 如果占用的计算资源越少，那么空间复杂度越低。

我们要选择复杂度低的算法，衡量好空间和时间的消耗，选出适合特定场景的算法。

这两个复杂度维度的量化过程都是一样的，所以我们这里主要介绍时间复杂度。

二、算法规模

我们要计算公式 1 + 2 + 3 + ... + 100，那么按照最直观的算法来写：

package main

import "fmt"

func sum(n int) int {
	total := 0
	// 从1加到N, 1+2+3+4+5+..+N
	for i := 1; i <= n; i++ {
		total = total + i
	}
	return total
}

func main() {
	fmt.Println(sum(100))
}

当 n = 10 时就等于我们要计算的公式。这个算法要循环 n-1 次，当 n 很小时，计算很快，但当 n 无限大的时候，计算很慢。

所以，算法衡量要衡量的是在不同 问题规模 n 下，算法的速度。

在这里，因为要循环计算 n-1 次，而当 n 无限大时，常数项基本忽略不计，所以这个算法的时间复杂度，我们用 O(n) 来表示。

我们有另外一种计算方式：

func sum2(n int) int {
	total := ((1 + n) * n) / 2
	return total
}

这次算法只需执行 1 次，所以这个算法的时间复杂度是 O(1)。可以看出，时间复杂度为 O(1) 的算法优于复杂度为 O(n) 的算法。

当然，还有指数级别的比如之前的汉诺塔算法，对数级别的，阶乘级别的复杂度，如 O(2^n)，O(n!)，O(logn) 等。

算法的优先级排列如下，一般排在上面的要优于排在下面的：

1. 常数复杂度：O(1)
2. 对数复杂度：O(logn)
3. 一次方复杂度：O(n)
4. 一次方乘对数复杂度：O(nlogn)
5. 乘方复杂度：O(n^2)，O(n^3)
6. 指数复杂度：O(2^n)
7. 阶乘复杂度：O(n!)
8. 无限大指数复杂度：O(n^n)

三、渐进符号

如何量化一个复杂度，到底有多复杂，计算机科学抽象出了几个复杂度渐进符号。

渐进符号如下：

O，ο，Θ，Ω，ω

分别读作：Omicron（大欧），omicron（小欧），Theta（西塔），Omega（大欧米伽），omega（小欧米伽）。

总结

记号	含义	通俗理解
Θ	紧确界	相当于"="
O	上界	相当于"<="
ο	非紧的上界	相当于"<"
Ω	下界	相当于">="
ω	非紧的下界	相当于">"

我们一般用 O 渐进上界来评估一个算法的时间复杂度，表示逼近的最坏情况。其他渐进符合基本不怎么使用。

算法复杂度主方法

有时候，我们要评估一个算法的复杂度，但是算法被分散为几个递归的子问题，这样评估起来很难，有一个数学公式可以很快地评估出来。

一、复杂度主方法

主方法，也可以叫主定理。对于那些用分治法，有递推关系式的算法，可以很快求出其复杂度。

定义如下：

如果对证明感兴趣的可以翻阅书籍：《算法导论》。如果觉得太难思考，可以跳过该节。

由于主定理的公式十分复杂，所以这里有一种比较简化的版本来计算：

二、举例

1. 二分搜索，每次问题规模减半，只查一个数，递推过程之外的查找复杂度为 O(1)，递推运算时间公式为：T(n) = T(n/2) + O(1)。
2. 快速排序，每次随机选一个数字作为划分进行排序，每次问题规模减半，递推过程之外的排序复杂度为 O(n)，递推运算时间递推公式为：T(n) = 2T(n/2) + O(n)。

按照简化版的主定理，可以知道：

二分查找：a = 1，b = 2，d = 0，可以知道 a = b^d，所以二分查找的时间复杂度为：O(logn)。

快速排序：a = 2，b = 2，d = 1，可以知道 a = b^d，所以快速排序的时间复杂度为：O(nlogn)。

强调：并非所有递推关系式都可应用主定理，但是大部分情况下都可以。

因为需要较多的数学知识，所以我们只简单介绍到这里。

常见数据结构及算法

数据结构主要用来组织数据，也作为数据的容器，载体。

各种各样的算法，都需要使用一定的数据结构来组织数据。

常见的典型数据结构有：

1. 链表
2. 栈和队列
3. 树
4. 图

上述可以延伸出各种各样的术语和结构，如列表，集合，哈希表，堆，优先队列，二叉树，红黑树，B+树以及各种变种等。

我们区别开数据结构和算法，是因为算法是更高层次的一种智慧结晶，目的就是为了解决问题，基本的算法分类有：

1. 排序算法
2. 查找算法
3. 图相关的算法
4. 其他的算法

计算机科学作为数学的一个分支，大部分的数学知识都是离散数学。我们学习微积分，都是连续的量，可是计算机处理的都是离散的量，数据不存在渐变，都是一个个离散数据。

所以针对离散的计算机科学来说，很多算法都是很简单，也是富含哲学的。 也就是说，现在已知的所有算法，都是严格定义的，是死的，是千篇一律的。作为解决日常生活的一种思路，不需要纠结算法是什么分类，只要知道有这种方法，在什么时候需要使用它就行了。

一般在日常工程开发中，也就是做软件，做网站，基本只使用到排序和查找算法，甚至有些情况下不需要使用。100%的日常开发场景是，我拿到一个数据存在数据库，你需要这个数据，我再帮你找出来。

我们会在后面的篇章介绍这些数据结构和算法。

链表

讲数据结构就离不开讲链表。因为数据结构是用来组织数据的，如何将一个数据关联到另外一个数据呢？链表可以将数据和数据之间关联起来，从一个数据指向另外一个数据。

一、链表

定义：

链表由一个个数据节点组成的，它是一个递归结构，要么它是空的，要么它存在一个指向另外一个数据节点的引用。

链表，可以说是最基础的数据结构。

最简单的链表如下：

package main

import "fmt"

type LinkNode struct {
	Data     int64
	NextNode *LinkNode
}

func main() {
	// 新的节点
	node := new(LinkNode)
	node.Data = 2

	// 新的节点
	node1 := new(LinkNode)
	node1.Data = 3
	node.NextNode = node1 // node1 链接到 node 节点上

	// 新的节点
	node2 := new(LinkNode)
	node2.Data = 4
	node1.NextNode = node2 // node2 链接到 node1 节点上
	// 按顺序打印数据
	nowNode := node
	for {
		if nowNode != nil {
			// 打印节点值
			fmt.Println(nowNode.Data)
			// 获取下一个节点
			nowNode = nowNode.NextNode
			continue
		}
		// 如果下一个节点为空，表示链表结束了
		break
	}

}

打印出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
2
3
4

结构体 LinkNode 有两个字段，一个字段存放数据 Data，另一个字典指向下一个节点 NextNode 。这种从一个数据节点指向下一个数据节点的结构，都可以叫做链表。

有些书籍，把链表做了很细的划分，比如单链表，双链表，循环单链表，循环双链表，其实没有必要强行分类，链表就是从一个数据指向另外一个数据，一种将数据和数据关联起来的结构而已。

好吧，我们还是要知道是什么。

1. 单链表，就是链表是单向的，像我们上面这个结构一样，可以一直往下找到下一个数据节点，它只有一个方向，它不能往回找。
2. 双链表，每个节点既可以找到它之前的节点，也可以找到之后的节点，是双向的。
3. 循环链表，就是它一直往下找数据节点，最后回到了自己那个节点，形成了一个回路。循环单链表和循环双链表的区别就是，一个只能一个方向走，一个两个方向都可以走。

我们来实现一个循环链表 Ring（集链表大成者），参考 Golang 标准库 container/ring：：

// 循环链表
type Ring struct {
	next, prev *Ring       // 前驱和后驱节点
	Value      interface{} // 数据
}

该循环链表有一个三个字段，next 表示后驱节点，prev 表示前驱节点，Value 表示值。

我们来分析该结构各操作的时间复杂度。

1.1.初始化循环链表

初始化一个空的循环链表：

package main

// 循环链表
type Ring struct {
	next, prev *Ring       // 前驱和后驱节点
	Value      interface{} // 数据
}

// 初始化空的循环链表，前驱和后驱都指向自己，因为是循环的
func (r *Ring) init() *Ring {
	r.next = r
	r.prev = r
	return r
}
func main() {
	r := new(Ring)
	r.init()
}

因为绑定前驱和后驱节点为自己，没有循环，时间复杂度为：O(1)。

创建一个指定大小 N 的循环链表，值全为空：

// 创建N个节点的循环链表
func New(n int) *Ring {
	if n <= 0 {
		return nil
	}
	r := new(Ring)
	p := r
	for i := 1; i < n; i++ {
		p.next = &Ring{prev: p}
		p = p.next
	}
	p.next = r
	r.prev = p
	return r
}

会连续绑定前驱和后驱节点，时间复杂度为：O(n)。

1.2.获取上一个或下一个节点

// 获取下一个节点
func (r *Ring) Next() *Ring {
	if r.next == nil {
		return r.init()
	}
	return r.next
}
// 获取上一个节点
func (r *Ring) Prev() *Ring {
	if r.next == nil {
		return r.init()
	}
	return r.prev
}

获取前驱或后驱节点，时间复杂度为：O(1)。

1.2.获取第 n 个节点

因为链表是循环的，当 n 为负数，表示从前面往前遍历，否则往后面遍历：

func (r *Ring) Move(n int) *Ring {
	if r.next == nil {
		return r.init()
	}
	switch {
	case n < 0:
		for ; n < 0; n++ {
			r = r.prev
		}
	case n > 0:
		for ; n > 0; n-- {
			r = r.next
		}
	}
	return r
}

因为需要遍历 n 次，所以时间复杂度为：O(n)。

1.3.添加节点

// 往节点A，链接一个节点，并且返回之前节点A的后驱节点
func (r *Ring) Link(s *Ring) *Ring {
	n := r.Next()
	if s != nil {
		p := s.Prev()
		r.next = s
		s.prev = r
		n.prev = p
		p.next = n
	}
	return n
}

添加节点的操作比较复杂，如果节点 s 是一个新的节点。

那么也就是在 r 节点后插入一个新节点 s，而 r 节点之前的后驱节点，将会链接到新节点后面，并返回 r 节点之前的第一个后驱节点 n，图如下：

可以看到插入新节点，会重新形成一个环，新节点 s 被插入了中间。

执行以下程序：

func linkNewTest() {
	// 第一个节点
	r := &Ring{Value: -1}
	// 链接新的五个节点
	r.Link(&Ring{Value: 1})
	r.Link(&Ring{Value: 2})
	r.Link(&Ring{Value: 3})
	r.Link(&Ring{Value: 4})

	node := r
	for {
		// 打印节点值
		fmt.Println(node.Value)

		// 移到下一个节点
		node = node.Next()
		//  如果节点回到了起点，结束
		if node == r {
			return
		}
	}
}

func main() {
	linkNewTest()
}

PS D:\Workspace\Go\src\projects\demo> go run main.go
-1
4
3
2
1

每次链接的是一个新节点，那么链会越来越长，仍然是一个环。因为只是更改链接位置，时间复杂度为：O(1)。

1.4.删除节点

// 删除节点后面的 n 个节点
func (r *Ring) Unlink(n int) *Ring {
	if n < 0 {
		return nil
	}
	return r.Link(r.Move(n + 1))
}

将循环链表的后面几个节点删除。

执行：

func deleteTest() {
	// 第一个节点
	r := &Ring{Value: -1}

	// 链接新的五个节点
	r.Link(&Ring{Value: 1})
	r.Link(&Ring{Value: 2})
	r.Link(&Ring{Value: 3})
	r.Link(&Ring{Value: 4})

	temp := r.Unlink(3) // 解除了后面两个节点
	// 打印原来的节点
	node := r
	for {
		// 打印节点值
		fmt.Println(node.Value)
		// 移到下一个节点
		node = node.Next()
		//  如果节点回到了起点，结束
		if node == r {
			break
		}
	}
	fmt.Println("------")
	// 打印被切断的节点
	node = temp
	for {
		// 打印节点值
		fmt.Println(node.Value)
		// 移到下一个节点
		node = node.Next()

		//  如果节点回到了起点，结束
		if node == temp {
			break
		}
	}
}
func main() {
	deleteTest()
}

输出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
-1
1
------
4
3
2

删除循环链表后面的三个节点：r.Unlink(3)。

可以看到节点 r 后面的两个节点被切断了，然后分成了两个循环链表，r 所在的链表变成了 -1，1。

而切除的那部分形成一个新循环链表是 4 3 2，并且返回给了用户。

因为只要定位要删除的节点位置，然后进行链接：r.Link(r.Move(n + 1))，所以时间复杂度为：O(n)+O(1)=O(n)

1.5.获取链表长度

// 查看循环链表长度
func (r *Ring) Len() int {
	n := 0
	if r != nil {
		n = 1
		for p := r.Next(); p != r; p = p.next {
			n++
		}
	}
	return n
}

通过循环，当引用回到自己，那么计数完毕，时间复杂度：O(n)。

因为循环链表还不够强壮，不知道起始节点是哪个，计数链表长度还要遍历，所以用循环链表实现的双端队列就出现了，一般具体编程都使用更高层次的数据结构。

详细可查看栈和队列章节。

二、数组和链表

数组是编程语言作为一种基本类型提供出来的，相同数据类型的元素按一定顺序排列的集合。

它的作用只有一种：存放数据，让你很快能找到存的数据。如果你不去额外改进它，它就只是存放数据而已，它不会将一个数据节点和另外一个数据节点关联起来。比如建立一个大小为5的数组 array:

package main

import "fmt"

//  打印出：
//  [0 0 0 0 0]
//  [8 9 7 0 0]
//  7
func main() {
	array := [5]int64{}
	fmt.Println(array)
	array[0] = 8
	array[1] = 9
	array[2] = 7
	fmt.Println(array)
	fmt.Println(array[2])
}

我们可以通过下标 0，1，2 来获取到数组中的数据，下标 0，1，2 就表示数据的位置，排第一位，排第二位，我们也可以把指定位置的数据替换成另外一个数据。

数组这一数据类型，是被编程语言高度抽象封装的结构，下标 会转换成 虚拟内存地址，然后操作系统会自动帮我们进行寻址，这个寻址过程是特别快的，所以往数组的某个下标取一个值和放一个值，时间复杂度都为 O(1)。

它是一种将 虚拟内存地址 和 数据元素 映射起来的内置语法结构，数据和数据之间是挨着，存放在一个连续的内存区域，每一个固定大小（8字节）的内存片段都有一个虚拟的地址编号。当然这个虚拟内存不是真正的内存，每个程序启动都会有一个虚拟内存空间来映射真正的内存，这是计算机组成的内容，和数据结构也有点关系，我们会在另外的高级专题讲，这里就不展开了。

用数组也可以实现链表，比如定义一个数组 [5]Value，值类型为一个结构体 Value ：

package main

import "fmt"

func ArrayLink() {
	type Value struct {
		Data      string
		NextIndex int64
	}

	var array [5]Value          // 五个节点的数组
	array[0] = Value{"I", 3}    // 下一个节点的下标为3
	array[1] = Value{"Army", 4} // 下一个节点的下标为4
	array[2] = Value{"You", 1}  // 下一个节点的下标为1
	array[3] = Value{"Love", 2} // 下一个节点的下标为2
	array[4] = Value{"!", -1}   // -1表示没有下一个节点
	node := array[0]
	for {
		fmt.Println(node.Data)
		if node.NextIndex == -1 {
			break
		}
		node = array[node.NextIndex]
	}
}

func main() {
	ArrayLink()
}

打印出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
I
Love
You
Army
!

获取某个 下标 的数据，通过该数据可以知道 下一个数据的下标 是什么，然后拿出该下标的数据，继续往下做。问题是，有时候需要做删除，移动等各种操作，而数组的大小是固定的，需要大量空间移动，所以某些情况下，数组的效率很低。

数组和链表是两个不同的概念。一个是编程语言提供的基本数据类型，表示一个连续的内存空间，可通过一个索引访问数据。另一个是我们定义的数据结构，通过一个数据节点，可以定位到另一个数据节点，不要求连续的内存空间。

数组的优点是占用空间小，查询快，直接使用索引就可以获取数据元素，缺点是移动和删除数据元素要大量移动空间。

链表的优点是移动和删除数据元素速度快，只要把相关的数据元素重新链接起来，但缺点是占用空间大，查找需要遍历。

很多其他的数据结构都由数组和链表配合实现的。

三、总结

链表 和 数组 可以用来辅助构建各种基本数据结构。

数据结构名字特别多，在以后的计算机生涯中，有些自己造的数据结构，或者不常见的别人造的数据结构，不知道叫什么名字是很正常的。我们只需知道常见的数据结构即可，方便与其他程序员交流。

可变长数组

因为数组大小是固定的，当数据元素特别多时，固定的数组无法储存这么多的值，所以可变长数组出现了，这也是一种数据结构。在 Golang 语言中，可变长数组被内置在语言里面：切片 slice。

slice 是对底层数组的抽象和控制。它是一个结构体：

type slice struct {
	array unsafe.Pointer
	len int
	cap int
}

1. 指向底层数组的指针。( Golang 语言是没有操作原始内存的指针的，所以 unsafe 包提供相关的对内存指针的操作，一般情况下非专业人员勿用)
2. 切片的真正长度，也就是实际元素占用的大小。
3. 切片的容量，底层固定数组的长度。

每次可以初始化一个固定容量的切片，切片内部维护一个固定大小的数组。当 append 新元素时，固定大小的数组不够时会自动扩容，如：

package main

import (
	"fmt"
	"unsafe"
)

type slice struct {
	array unsafe.Pointer
	len   int
	cap   int
}

func main() {
	// 创建一个容量为2的切片
	array := make([]int, 0, 2)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
	// 虽然 append 但是没有赋予原来的变量 array
	_ = append(array, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
	_ = append(array, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
	_ = append(array, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)

	fmt.Println("-------")
	// 赋予回原来的变量
	array = append(array, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
	array = append(array, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
	array = append(array, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
	array = append(array, 1, 1, 1, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
	array = append(array, 1, 1, 1, 1, 1, 1, 1, 1, 1)
	fmt.Println("cap", cap(array), "len", len(array), "array:", array)
}

输出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
cap 2 len 0 array: []
cap 2 len 0 array: []
cap 2 len 0 array: []
cap 2 len 0 array: []
-------
cap 2 len 1 array: [1]
cap 2 len 2 array: [1 1]
cap 4 len 3 array: [1 1 1]
cap 8 len 7 array: [1 1 1 1 1 1 1]
cap 16 len 16 array: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]

我们可以看到 Golang 的切片无法原地 append，每次添加元素时返回新的引用地址，必须把该引用重新赋予之前的切片变量。并且，当容量不够时，会自动倍数递增扩容。事实上，Golang 在切片长度大于 1024 后，会以接近于 1.25 倍进行容量扩容。

具体可参考标准库 runtime 下的 slice.go 文件。

一、实现可变长数组

我们来实现一个简单的，存放整数的，可变长的数组版本。

因为 Golang 的限制，不允许使用 [n]int 来创建一个固定大小为 n 的整数数组，只允许使用常量来创建大小。

所以我们这里会使用切片的部分功能来代替数组，虽然切片本身是可变长数组，但是我们不会用到它的 append 功能，只把它当数组用。

import "sync"

// Array 可变长数组
type Array struct {
	array []int      // 固定大小的数组，用满容量和满大小的切片来代替
	len   int        // 真正长度
	cap   int        // 容量
	lock  sync.Mutex // 为了并发安全使用的锁
}

1.1. 初始化数组

创建一个 len 个元素，容量为 cap 的可变长数组：

// Make 新建一个可变长数组
func Make(len, cap int) *Array {
	s := new(Array)
	if len > cap {
		panic("len large than cap")
	}
	// 把切片当数组用
	array := make([]int, cap, cap)

	// 元数据
	s.array = array
	s.cap = cap
	s.len = 0
	return s
}

主要利用满容量和满大小的切片来充当固定数组，结构体 Array 里面的字段 len 和 cap 来控制值的存取。不允许设置 len > cap 的可变长数组。

时间复杂度为：O(1)，因为分配内存空间和设置几个值是常数时间。

1.2. 添加元素

// Append 增加一个元素
func (a *Array) Append(element int) {
	// 并发锁
	a.lock.Lock()
	defer a.lock.Lock()

	// 大小等于容量，表示没多余位置了
	if a.len == a.cap {
		// 没容量，数组要扩容，扩容到两倍
		newCap := 2 * a.len

		// 如果之前的容量为0，那么新容量为1
		if a.cap == 0 {
			newCap = 1
		}
		newArray := make([]int, newCap, newCap)

		// 把老数组的数据移动到新数组
		for k, v := range a.array {
			newArray[k] = v
		}

		// 替换数组
		a.array = newArray
		a.cap = newCap
	}
	// 把元素放在数组里
	a.array[a.len] = element
	// 真实长度+1
	a.len = a.len + 1
}

首先添加一个元素到可变长数组里，会加锁，这样会保证并发安全。然后将值放在数组里：a.array[a.len] = element，然后 len + 1，表示真实大小又多了一个。

当真实大小 len = cap 时，表明位置都用完了，没有多余的空间放新值，那么会创建一个固定大小 2*len 的新数组来替换老数组：a.array = newArray，当然容量也会变大：a.cap = newCap。如果一开始设置的容量 cap = 0，那么新的容量会是从 1 开始。

添加元素中，耗时主要在老数组中的数据移动到新数组，时间复杂度为：O(n)。当然，如果容量够的情况下，时间复杂度会变为：O(1)。

如何添加多个元素：

// AppendMany 增加多个元素
func (a *Array) AppendMany(element ...int) {
	for _, v := range element {
		a.Append(v)
	}
}

只是简单遍历一下，调用 Append 函数。其中 ...int 是 Golang 的语言特征，表示多个函数变量。

1.3. 获取指定下标元素

// Get 获取某个下标的元素
func (a *Array) Get(index int) int {
	// 越界了
	if a.len == 0 || index >= a.len {
		panic("index over len")
	}
	return a.array[index]
}

当可变长数组的真实大小为0，或者下标 index 超出了真实长度 len ，将会 panic 越界。

因为只获取下标的值，所以时间复杂度为 O(1)。

1.4. 获取真实长度和容量

// Len 返回真实长度
func (a *Array) Len() int {
	return a.len
}

// Cap 返回容量
func (a *Array) Cap() int {
	return a.cap
}

时间复杂度为 O(1)。

1.5. 示例

现在我们来运行完整的可变长数组的例子：

package main

import (
	"fmt"
	"sync"
)

// Array 可变长数组
type Array struct {
	array []int      // 固定大小的数组，用满容量和满大小的切片来代替
	len   int        // 真正长度
	cap   int        // 容量
	lock  sync.Mutex // 为了并发安全使用的锁
}

// Make 新建一个可变长数组
func Make(len, cap int) *Array {
	s := new(Array)
	if len > cap {
		panic("len large than cap")
	}
	// 把切片当数组用
	array := make([]int, cap, cap)

	// 元数据
	s.array = array
	s.cap = cap
	s.len = 0
	return s
}

// Append 增加一个元素
func (a *Array) Append(element int) {
	// 并发锁
	a.lock.Lock()
	defer a.lock.Unlock()

	// 大小等于容量，表示没多余位置了
	if a.len == a.cap {
		// 没容量，数组要扩容，扩容到两倍
		newCap := 2 * a.len

		// 如果之前的容量为0，那么新容量为1
		if a.cap == 0 {
			newCap = 1
		}
		newArray := make([]int, newCap, newCap)

		// 把老数组的数据移动到新数组
		for k, v := range a.array {
			newArray[k] = v
		}

		// 替换数组
		a.array = newArray
		a.cap = newCap
	}
	// 把元素放在数组里
	a.array[a.len] = element
	// 真实长度+1
	a.len = a.len + 1
}

// AppendMany 增加多个元素
func (a *Array) AppendMany(element ...int) {
	for _, v := range element {
		a.Append(v)
	}
}

// Get 获取某个下标的元素
func (a *Array) Get(index int) int {
	// 越界了
	if a.len == 0 || index >= a.len {
		panic("index over len")
	}
	return a.array[index]
}

// Len 返回真实长度
func (a *Array) Len() int {
	return a.len
}

// Cap 返回容量
func (a *Array) Cap() int {
	return a.cap
}

// Print 辅助打印
func Print(array *Array) (result string) {
	result = "["
	for i := 0; i < array.Len(); i++ {
		// 第一个元素
		if i == 0 {
			result = fmt.Sprintf("%s%d", result, array.Get(i))
			continue
		}
		result = fmt.Sprintf("%s %d", result, array.Get(i))
	}
	result = result + "]"
	return
}
func main() {
	// 创建一个容量为3的动态数组
	a := Make(0, 3)
	fmt.Println("cap", a.Cap(), "len", a.Len(), "array:", Print(a))
	// 增加一个元素
	a.Append(10)
	fmt.Println("cap", a.Cap(), "len", a.Len(), "array:", Print(a))

	// 增加一个元素
	a.Append(9)
	fmt.Println("cap", a.Cap(), "len", a.Len(), "array:", Print(a))

	// 增加多个元素
	a.AppendMany(8, 7)
	fmt.Println("cap", a.Cap(), "len", a.Len(), "array:", Print(a))
}

将打印出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
cap 3 len 0 array: []
cap 3 len 1 array: [10]      
cap 3 len 2 array: [10 9]    
cap 6 len 4 array: [10 9 8 7]

可以看到，容量会自动翻倍。

二、总结

可变长数组在实际开发上，经常会使用到，其在固定大小数组的基础上，会自动进行容量扩展。

因为这一数据结构的使用频率太高了，所以，Golang 自动提供了这一数据类型：切片（可变长数组）。大家一般开发过程中，直接使用这一类型即可。

栈和队列

一、栈 Stack 和队列 Queue

二、实现数组栈 ArrayStack

数组形式的下压栈，后进先出:

主要使用可变长数组来实现。

// 数组栈，后进先出
type ArrayStack struct {
	array []string   // 底层切片
	size  int        // 栈的元素数量
	lock  sync.Mutex // 为了并发安全使用的锁
}

我们来分析它的各操作。

2.1.入栈

// 入栈
func (stack *ArrayStack) Push(v string) {
	stack.lock.Lock()
	defer stack.lock.Unlock()

	// 放入切片中，后进的元素放在数组最后面
	stack.array = append(stack.array, v)

	// 栈中元素数量+1
	stack.size = stack.size + 1
}

将元素入栈，会先加锁实现并发安全。

入栈时直接把元素放在数组的最后面，然后元素数量加 1。性能损耗主要花在切片追加元素上，切片如果容量不够会自动扩容，底层损耗的复杂度我们这里不计，所以时间复杂度为 O(1)。

2.2.出栈

// 出栈
func (stack *ArrayStack) Pop() string {
	stack.lock.Lock()
	defer stack.lock.Unlock()

	// 栈中元素已空
	if stack.size == 0 {
		panic("empty")
	}
	// 栈顶元素
	v := stack.array[stack.size-1]

	// 切片收缩，但可能占用空间越来越大
	// stack.array = stack.array[0 : stack.size-1]

	// 创建新的数组，空间占用不会越来越大，但可能移动元素次数过多
	newArray := make([]string, stack.size-1, stack.size-1)
	for i := 0; i < stack.size-1; i++ {
		newArray[i] = stack.array[i]
	}
	stack.array = newArray

	// 栈中元素数量-1
	stack.size = stack.size - 1
	return v
}

元素出栈，会先加锁实现并发安全。

如果栈大小为0，那么不允许出栈，否则从数组的最后面拿出元素。

元素取出后:

1. 如果切片偏移量向前移动 stack.array[0 : stack.size-1]，表明最后的元素已经不属于该数组了，数组变相的缩容了。此时，切片被缩容的部分并不会被回收，仍然占用着空间，所以空间复杂度较高，但操作的时间复杂度为：O(1)。
2. 如果我们创建新的数组 newArray，然后把老数组的元素复制到新数组，就不会占用多余的空间，但移动次数过多，时间复杂度为：O(n)。

最后元素数量减一，并返回值。

2.3.获取栈顶元素

// 获取栈顶元素
func (stack *ArrayStack) Peek() string {
	// 栈中元素已空
	if stack.size == 0 {
		panic("empty")
	}

	// 栈顶元素值
	v := stack.array[stack.size-1]
	return v
}

获取栈顶元素，但不出栈。和出栈一样，时间复杂度为：O(1)。

2.4.获取栈大小和判定是否为空

// 栈大小
func (stack *ArrayStack) Size() int {
	return stack.size
}

// 栈是否为空
func (stack *ArrayStack) IsEmpty() bool {
	return stack.size == 0
}

一目了然，时间复杂度都是：O(1)。

2.5.示例

func main() {
	arrayStack := new(ArrayStack)
	arrayStack.Push("cat")
	arrayStack.Push("dog")
	arrayStack.Push("hen")
	fmt.Println("size:", arrayStack.Size())
	fmt.Println("pop:", arrayStack.Pop())
	fmt.Println("pop:", arrayStack.Pop())
	fmt.Println("size:", arrayStack.Size())
	arrayStack.Push("drag")
	fmt.Println("pop:", arrayStack.Pop())
}

PS D:\Workspace\Go\src\projects\demo> go run main.go
size: 3
pop: hen
pop: dog
size: 1
pop: drag

三、实现链表栈 LinkStack

链表形式的下压栈，后进先出：

// 链表栈，后进先出
type LinkStack struct {
	root *LinkNode  // 链表起点
	size int        // 栈的元素数量
	lock sync.Mutex // 为了并发安全使用的锁
}

// 链表节点
type LinkNode struct {
	Next *LinkNode
	Value string
}

我们来分析它的各操作。

3.1.入栈

// 入栈
func (stack *LinkStack) Push(v string) {
	stack.lock.Lock()
	defer stack.lock.Unlock()

	// 如果栈顶为空，那么增加节点
	if stack.root == nil {
		stack.root = new(LinkNode)
		stack.root.Value = v
	} else {
		// 否则新元素插入链表的头部
		// 原来的链表
		preNode := stack.root

		// 新节点
		newNode := new(LinkNode)
		newNode.Value = v

		// 原来的链表链接到新元素后面
		newNode.Next = preNode

		// 将新节点放在头部
		stack.root = newNode
	}

	// 栈中元素数量+1
	stack.size = stack.size + 1
}

将元素入栈，会先加锁实现并发安全。

如果栈里面的底层链表为空，表明没有元素，那么新建节点并设置为链表起点：stack.root = new(LinkNode)。

否则取出老的节点：preNode := stack.root，新建节点：newNode := new(LinkNode)，然后将原来的老节点链接在新节点后面： newNode.Next = preNode，最后将新节点设置为链表起点 stack.root = newNode。

时间复杂度为：O(1)。

3.2.出栈

// 出栈
func (stack *LinkStack) Pop() string {
	stack.lock.Lock()
	defer stack.lock.Unlock()

	// 栈中元素已空
	if stack.size == 0 {
		panic("empty")
	}

	// 顶部元素要出栈
	topNode := stack.root
	v := topNode.Value

	// 将顶部元素的后继链接链上
	stack.root = topNode.Next
	
	// 栈中元素数量-1
	stack.size = stack.size - 1
	return v
}

元素出栈。如果栈大小为0，那么不允许出栈。

直接将链表的第一个节点 topNode := stack.root 的值取出，然后将表头设置为链表的下一个节点：stack.root = topNode.Next，相当于移除了链表的第一个节点。

时间复杂度为：O(1)。

3.3.获取栈顶元素

// 获取栈顶元素
func (stack *LinkStack) Peek() string {
	// 栈中元素已空
	if stack.size == 0 {
		panic("empty")
	}

	// 栈顶元素值
	v := stack.root.Value
	return v
}

获取栈顶元素，但不出栈。和出栈一样，时间复杂度为：O(1)。

3.4.获取栈大小和判定是否为空

// 栈大小
func (stack *LinkStack) Size() int {
	return stack.size
}

// 栈是否为空
func (stack *LinkStack) IsEmpty() bool {
	return stack.size == 0
}

3.5.示例

func main() {
	arrayStack := new(LinkStack)
	arrayStack.Push("cat")
	arrayStack.Push("dog")
	arrayStack.Push("hen")
	fmt.Println("size:", arrayStack.Size())
	fmt.Println("pop:", arrayStack.Pop())
	fmt.Println("pop:", arrayStack.Pop())
	fmt.Println("size:", arrayStack.Size())
	arrayStack.Push("drag")
	fmt.Println("pop:", arrayStack.Pop())
}

输出：

size: 3
pop: hen
pop: dog
size: 1
pop: drag

四、实现数组队列 ArrayQueue

队列先进先出，和栈操作顺序相反，我们这里只实现入队，和出队操作，其他操作和栈一样。

// 数组队列，先进先出
type ArrayQueue struct {
	array []string   // 底层切片
	size  int        // 队列的元素数量
	lock  sync.Mutex // 为了并发安全使用的锁
}

4.1.入队

// 入队
func (queue *ArrayQueue) add(v string) {
	queue.lock.Lock()
	defer queue.lock.Unlock()

	// 放入切片中，后进的元素放在数组最后面
	queue.array = append(queue.array, v)

	// 队中元素数量+1
	queue.size = queue.size + 1
}

直接将元素放在数组最后面即可，和栈一样，时间复杂度为：O(n)。

4.2.出队

// 出队
func (queue *ArrayQueue) Remove() string {
	queue.lock.Lock()
	defer queue.lock.Unlock()

	// 队中元素已空
	if queue.size == 0 {
		panic("empty")
	}

	// 队列最前面元素
	v := queue.array[0]
	/*	直接原位移动，但缩容后继的空间不会被释放
		for i := 1; i < queue.size; i++ {
			// 从第一位开始进行数据移动
			queue.array[i-1] = queue.array[i]
		}
		// 原数组缩容
		queue.array = queue.array[0 : queue.size-1]
	*/

	// 创建新的数组，移动次数过多
	newArray := make([]string, queue.size-1, queue.size-1)
	for i := 1; i < queue.size; i++ {
		// 从老数组的第一位开始进行数据移动
		newArray[i-1] = queue.array[i]
	}
	queue.array = newArray

	// 队中元素数量-1
	queue.size = queue.size - 1
	return v
}

出队，把数组的第一个元素的值返回，并对数据进行空间挪位，挪位有两种：

1. 原地挪位，依次补位 queue.array[i-1] = queue.array[i]，然后数组缩容：queue.array = queue.array[0 : queue.size-1]，但是这样切片缩容的那部分内存空间不会释放。
2. 创建新的数组，将老数组中除第一个元素以外的元素移动到新数组。

时间复杂度是：O(n)。

五、实现链表队列 LinkQueue

队列先进先出，和栈操作顺序相反，我们这里只实现入队，和出队操作，其他操作和栈一样。

// 链表队列，先进先出
type LinkQueue struct {
	root *LinkNode // 链表起点
	size int // 队列的元素数量
	lock sync.Mutex // 为了并发安全使用的锁
}

// 链表结点
type LinkNode struct {
	Next *LinkNode
	Value string
}

5.1.入队

// 入队
func (queue *LinkQueue) Add(v string) {
	queue.lock.Lock()
	defer queue.lock.Unlock()
	// 如果栈顶为空，那么增加节点
	if queue.root == nil {
		queue.root = new(LinkNode)
		queue.root.Value = v
	} else {
		// 否则新元素插入链表的末尾
		// 新节点
		newNode := new(LinkNode)
		newNode.Value = v

		// 一直遍历到链表尾部
		nowNode := queue.root
		for nowNode.Next != nil {
			nowNode = nowNode.Next
		}
		// 新节点放在链表尾部
		nowNode.Next = newNode
	}

	// 队中元素数量+1
	queue.size = queue.size + 1
}

将元素放在链表的末尾，所以需要遍历链表，时间复杂度为：O(n)。

5.2.出队

// 出队
func (queue *LinkQueue) Remove() string {
	queue.lock.Lock()
	defer queue.lock.Unlock()

	// 队中元素已空
	if queue.size == 0 {
		panic("empty")
	}

	// 顶部元素要出队
	topNode := queue.root
	v := topNode.Value

	// 将顶部元素的后继链接链上
	queue.root = topNode.Next

	// 队中元素数量-1
	queue.size = queue.size - 1

	return v
}

链表第一个节点出队即可，时间复杂度为：O(1)。

列表

一、列表 List

我们又经常听到 列表 List 数据结构，其实这只是更宏观的统称，表示存放数据的队列。

列表 List：可以存放数据的数据结构，数据按顺序排列，可以依次入队和出队，

列表有序号关系，可以取出某个序号的数据。先进先出的 队列 (queue) 和先进后出的 栈（stack） 都是列表。

大家也经常听说一种叫 线性表 的数据结构，表示具有相同特性的数据元素的有限序列，实际上就是 列表 的同义词。

我们一般写算法进行数据计算，数据处理，都需要有个地方来存数据，我们可以使用封装好的数据结构 List。

列表的实现有 顺序表示 或 链式表示。

顺序表示：指的是用一组 地址连续的存储单元 依次存储线性表的数据元素，称为线性表的 顺序存储结构。它以 物理位置相邻 来表示线性表中数据元素间的逻辑关系，可随机存取表中任一元素。顺序表示的又叫 顺序表，也就是用数组来实现的列表。

链式表示：指的是用一组 任意的存储单元 存储线性表中的数据元素，称为线性表的 链式存储结构。它的存储单元可以是连续的，也可以是不连续的。在表示数据元素之间的逻辑关系时，除了存储其本身的信息之外，还需存储一个指示其直接后继的信息，也就是用链表来实现的列表。

我们在前面已经实现过这两种表示的数据结构：先进先出的 队列 (queue) 和先进后出的 栈（stack）。

接下来我们会来实现链表形式的双端列表，也叫双端队列，这个数据结构应用场景更广泛一点。在实际工程应用上，缓存数据库 Redis 的 列表List 基本类型就是用它来实现的。

二、实现双端列表

双端列表，也可以叫双端队列。

我们会用双向链表来实现这个数据结构：

// DoubleList 双端列表，双端队列
type DoubleList struct {
	head *ListNode  // 指向链表头部
	tail *ListNode  // 指向链表尾部
	len  int        // 列表长度
	lock sync.Mutex // 为了进行并发安全pop弹出操作
}

// ListNode 列表节点
type ListNode struct {
	pre   *ListNode // 前驱节点
	next  *ListNode // 后驱节点
	value string    // 值
}

设计结构体 DoubleList 指向队列头部 head 和尾部 tail 的指针字段，方便找到链表最前和最后的节点。

链表节点之间是双向链接的，链表的第一个元素的前驱节点为 nil，最后一个元素的后驱节点也为 nil。

我们实现的双端列表和 Golang 标准库 container/list 中实现的不一样，感兴趣的可以阅读标准库的实现。

2.1.列表节点普通操作

// GetValue 获取节点值
func (node *ListNode) GetValue() string {
	return node.value
}

// GetPre 获取节点前驱节点
func (node *ListNode) GetPre() *ListNode {
	return node.pre
}

// GetNext 获取节点后驱节点
func (node *ListNode) GetNext() *ListNode {
	return node.next
}

// HashNext 是否存在后驱节点
func (node *ListNode) HashNext() bool {
	return node.pre != nil
}

// HashNext 是否存在后驱节点
func (node *ListNode) HashPre() bool {
	return node.next != nil
}

// IsNil 是否为空节点
func (node *ListNode) IsNil() bool {
	return node.next != nil
}

// Len 返回列表长度
func (list *DoubleList) Len() int {
	return list.len
}

以上是对节点结构体 ListNode 的操作，主要判断节点是否为空，有没有后驱和前驱节点，返回值等，时间复杂度都是 O(1)。

2.2.从头部开始某个位置前插入新节点

我们参考数组下标，下标从0开始。从双端列表的头部，插入新的节点。

// AddNodeFromHead 从头部开始，添加节点到第N+1个元素之前，
// N=0表示添加到第一个元素之前，表示新节点成为新的头部，
// N=1表示添加到第二个元素之前，以此类推
func (list *DoubleList) AddNodeFromHead(n int, v string) {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()
	// 如果索引超过或等于列表长度，一定找不到，直接panic
	if n != 0 && n >= list.len {
		panic("index out")
	}

	// 先找出头部
	node := list.head

	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}

	// 新节点
	newNode := new(ListNode)
	newNode.value = v

	// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
	if node.IsNil() {
		list.head = newNode
		list.tail = newNode
	} else {
		// 定位到的节点，它的前驱
		pre := node.pre

		// 如果定位到的节点前驱为nil，那么定位到的节点为链表头部，需要换头部
		if pre.IsNil() {
			// 将新节点链接在老头部之前
			newNode.next = node
			node.pre = newNode
			// 新节点成为头部
			list.head = newNode
		} else {
			// 将新节点插入到定位到的节点之前
			// 定位到的节点的前驱节点 pre 现在链接到新节点上
			pre.next = newNode
			newNode.pre = pre

			// 定位到的节点的后驱节点 node.next 现在链接到新节点上
			node.next.pre = newNode
			newNode.next = node.next
		}
	}
	// 列表长度+1
	list.len = list.len + 1
}

首先加锁实现并发安全：

    // 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()

然后判断索引是否超出列表长度，其中 n=0 表示要成为新的头部节点，我们放过它：

	// 如果索引超过或等于列表长度，一定找不到，直接panic
	if n != 0 && n >= list.len {
		panic("index out")
	}

如果 n=0 表示要插入到第一个节点之前，也就是新节点想成为新的链表头部。

如果 n=1 表示要插入到第二个节点之前，新节点成为第二个节点，以此类推。

首先，找出列表的头部：

    node := list.head

然后往后面遍历，定位到索引 n 指定的节点 node，我们要在这个节点之前插入新的节点：

	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}

接着初始化新节点：

    newNode := new(ListNode)

定位到的节点有三种情况，我们需要在该节点之前插入新节点：

第一种情况，判断定位到的节点 node 是否为空，如果为空，表明列表没有元素，将新节点设置为新头部和新尾部即可：

	// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
	if node.IsNil() {
		list.head = newNode
		list.tail = newNode
	}

否则，我们要插入新的节点到非空的列表上。 我们找到定位到的节点的前驱节点：pre := node.pre，我们要把新节点变成定位到的节点的前驱节点，之前的前驱节点 pre 要往前顺延。

第二种情况，如果前驱节点为空：pre.IsNil()，表明定位到的节点 node 为头部，那么新节点要取代它，成为新的头部：

		if pre.IsNil() {
			// 将新节点链接在老头部之前
			newNode.next = node
			node.pre = newNode
			// 新节点成为头部
			list.head = newNode
		}

新节点成为新的头部，需要将新节点的后驱设置为老头部：newNode.next = node，老头部的前驱为新头部：node.pre = newNode，并且新头部变化：list.head = newNode。

第三种情况，如果定位到的节点的前驱节点不为空，表明定位到的节点 node 不是头部节点，那么我们只需将新节点链接到节点 node 之前即可：

			// 定位到的节点的前驱节点 pre 现在链接到新节点前
			pre.next = newNode
			newNode.pre = pre

			// 定位到的节点链接到新节点之后
			newNode.next = node
			node.pre = newNode

先将定位到的节点的前驱节点和新节点绑定，因为现在新节点插在前面了，把定位节点的前驱节点的后驱设置为新节点：pre.next = newNode，新节点的前驱设置为定位节点的前驱节点：newNode.pre = pre。

同时，定位到的节点现在要链接到新节点之后，所以新节点的后驱设置为：newNode.next = node，定位到的节点的前驱设置为：node.pre = newNode。

当然插入新节点的最后，我们要将链表长度加一：

    // 列表长度+1
    list.len = list.len + 1

大部分时间花在遍历位置上，如果 n=0，那么时间复杂度为 O(1)，否则为 O(n)。

2.3.从尾部开始某个位置后插入新节点

// AddNodeFromTail 从尾部开始，添加节点到第N+1个元素之后，N=0表示添加到第一个元素之后，表示新节点成为新的尾部，N=1表示添加到第二个元素之后，以此类推
func (list *DoubleList) AddNodeFromTail(n int, v string) {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()

	// 如果索引超过或等于列表长度，一定找不到，直接panic
	if n != 0 && n >= list.len {
		panic("index out")
	}

	// 先找出尾部
	node := list.tail
	// 往前遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.pre
	}
	// 新节点
	newNode := new(ListNode)
	newNode.value = v

	// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
	if node.IsNil() {
		list.head = newNode
		list.tail = newNode
	} else {
		// 定位到的节点，它的后驱
		next := node.next
		// 如果定位到的节点后驱为nil，那么定位到的节点为链表尾部，需要换尾部
		if next.IsNil() {
			// 将新节点链接在老尾部之后
			node.next = newNode
			newNode.pre = node

			// 新节点成为尾部
			list.tail = newNode
		} else {
			// 将新节点插入到定位到的节点之后
			// 新节点链接到定位到的节点之后
			newNode.pre = node
			node.next = newNode

			// 定位到的节点的后驱节点链接在新节点之后
			newNode.next = next
			next.pre = newNode
		}
	}
	// 列表长度+1
	list.len = list.len + 1
}

操作和头部插入节点相似，自行分析。

2.4.从头部开始某个位置获取列表节点

// IndexFromHead 从头部开始往后找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromHead(n int) *ListNode {
	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}

	// 获取头部节点
	node := list.head

	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}
	return node
}

如果索引超出或等于列表长度，那么找不到节点，返回空。

否则从头部开始遍历，拿到节点。

时间复杂度为：O(n)。

2.5.从尾部开始某个位置获取列表节点

// IndexFromTail 从尾部开始往前找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromTail(n int) *ListNode {
	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}

	// 获取尾部节点
	node := list.tail
	// 往前遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.pre
	}
	return node
}

操作和从头部获取节点一样，请自行分析。

2.6.从头部开始移除并返回某个位置的节点

获取某个位置的元素，并移除它。

// PopFromHead 从头部开始往后找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromHead(n int) *ListNode {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()
	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}
	// 获取头部
	node := list.head

	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}

	// 移除的节点的前驱和后驱
	pre := node.pre
	next := node.next
	// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
	if pre.IsNil() && next.IsNil() {
		list.head = nil
		list.tail = nil
	} else if pre.IsNil() {
		// 表示移除的是头部节点，那么下一个节点成为头节点
		list.head = next
		next.pre = nil
	} else if next.IsNil() {
		// 表示移除的是尾部节点，那么上一个节点成为尾节点
		list.tail = pre
		pre.next = nil
	} else {
		// 移除的是中间节点
		pre.next = next
		next.pre = pre
	}
	// 节点减一
	list.len = list.len - 1
	return node
}

首先加并发锁实现并发安全:

    // 加并发锁
    list.lock.Lock()
    defer list.lock.Unlock()

先判断索引是否超出列表长度，如果超出直接返回空指针。：

	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}

获取头部，然后遍历定位到第 N+1 个位置的元素:

	// 获取头部
	node := list.head
	
	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}

获取要移除的节点的前驱和后驱：

	// 移除的节点的前驱和后驱
	pre := node.pre
	next := node.next

定位到的并要移除的节点有三种情况发生，移除的是头部，尾部或者中间节点：

我们这么这里：

如果前驱和后驱都为空：

	// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
	if pre.IsNil() && next.IsNil() {
		list.head = nil
		list.tail = nil
	}

那么要移除的节点是链表中唯一的节点，直接将列表头部和尾部置空即可。

如果移除的是头部或尾部节点：

    else if pre.IsNil() {
		// 表示移除的是头部节点，那么下一个节点成为头节点
		list.head = next
		next.pre = nil
	} else if next.IsNil() {
		// 表示移除的是尾部节点，那么上一个节点成为尾节点
		list.tail = pre
		pre.next = nil
	} 

当前驱节点为空：pre.IsNil()，表示移除的是头部节点，那么头部节点的下一个节点要成为新的头部：list.head = next，并且这时新的头部前驱要设置为空：next.pre = nil。

同理，当后驱节点为空：next.IsNil()，表示移除的是尾部节点，需要将尾部节点的前一个节点设置为新的尾部：list.tail = pre，并且这时新的尾部后驱要设置为空：pre.next = nil。

如果移除的节点处于两个节点之间，那么将这两个节点链接起来即可:

    // 移除的是中间节点
    pre.next = next
    next.pre = pre

当然，最后列表长度减一：

    // 节点减一
	list.len = list.len - 1

主要的耗时用在定位节点上，其他的操作都是链表链接，可以知道时间复杂度为：O(n)。

2.7.从尾部开始移除并返回某个位置的节点

// PopFromTail 从尾部开始往前找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromTail(n int) *ListNode {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()
	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}
	// 获取尾
	node := list.tail

	// 往前遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.pre
	}

	// 移除的节点的前驱和后驱
	pre := node.pre
	next := node.next
	// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
	if pre.IsNil() && next.IsNil() {
		list.head = nil
		list.tail = nil
	} else if pre.IsNil() {
		// 表示移除的是头部节点，那么下一个节点成为头节点
		list.head = next
		next.pre = nil
	} else if next.IsNil() {
		// 表示移除的是尾部节点，那么上一个节点成为尾节点
		list.tail = pre
		pre.next = nil
	} else {
		// 移除的是中间节点
		pre.next = next
		next.pre = pre
	}
	// 节点减一
	list.len = list.len - 1
	return node
}

操作和从头部移除节点相似，请自行分析。

2.8.例子

package main

import (
	"fmt"
	"sync"
)

// DoubleList 双端列表，双端队列
type DoubleList struct {
	head *ListNode  // 指向链表头部
	tail *ListNode  // 指向链表尾部
	len  int        // 列表长度
	lock sync.Mutex // 为了进行并发安全pop弹出操作
}

// ListNode 列表节点
type ListNode struct {
	pre   *ListNode // 前驱节点
	next  *ListNode // 后驱节点
	value string    // 值
}

// GetValue 获取节点值
func (node *ListNode) GetValue() string {
	return node.value
}

// GetPre 获取节点前驱节点
func (node *ListNode) GetPre() *ListNode {
	return node.pre
}

// GetNext 获取节点后驱节点
func (node *ListNode) GetNext() *ListNode {
	return node.next
}

// HashNext 是否存在后驱节点
func (node *ListNode) HashNext() bool {
	return node.pre != nil
}

// HashPre 是否存在前驱节点
func (node *ListNode) HashPre() bool {
	return node.next != nil
}

// IsNil 是否为空节点
func (node *ListNode) IsNil() bool {
	return node == nil
}

// Len 返回列表长度
func (list *DoubleList) Len() int {
	return list.len
}

// AddNodeFromHead 从头部开始，添加节点到第N+1个元素之前，N=0表示添加到第一个元素之前，表示新节点成为新的头部，N=1表示添加到第二个元素之前，以此类推
func (list *DoubleList) AddNodeFromHead(n int, v string) {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()

	// 如果索引超过或等于列表长度，一定找不到，直接panic
	if n != 0 && n >= list.len {
		panic("index out")
	}

	// 先找出头部
	node := list.head

	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}

	// 新节点
	newNode := new(ListNode)
	newNode.value = v

	// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
	if node.IsNil() {
		list.head = newNode
		list.tail = newNode
	} else {
		// 定位到的节点，它的前驱
		pre := node.pre

		// 如果定位到的节点前驱为nil，那么定位到的节点为链表头部，需要换头部
		if pre.IsNil() {
			// 将新节点链接在老头部之前
			newNode.next = node
			node.pre = newNode
			// 新节点成为头部
			list.head = newNode
		} else {
			// 将新节点插入到定位到的节点之前
			// 定位到的节点的前驱节点 pre 现在链接到新节点前
			pre.next = newNode
			newNode.pre = pre

			// 定位到的节点链接到新节点之后
			newNode.next = node
			node.pre = newNode
		}

	}

	// 列表长度+1
	list.len = list.len + 1
}

// AddNodeFromTail 从尾部开始，添加节点到第N+1个元素之后，N=0表示添加到第一个元素之后，表示新节点成为新的尾部，N=1表示添加到第二个元素之后，以此类推
func (list *DoubleList) AddNodeFromTail(n int, v string) {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()

	// 如果索引超过或等于列表长度，一定找不到，直接panic
	if n != 0 && n >= list.len {
		panic("index out")
	}

	// 先找出尾部
	node := list.tail

	// 往前遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.pre
	}

	// 新节点
	newNode := new(ListNode)
	newNode.value = v

	// 如果定位到的节点为空，表示列表为空，将新节点设置为新头部和新尾部
	if node.IsNil() {
		list.head = newNode
		list.tail = newNode
	} else {
		// 定位到的节点，它的后驱
		next := node.next

		// 如果定位到的节点后驱为nil，那么定位到的节点为链表尾部，需要换尾部
		if next.IsNil() {
			// 将新节点链接在老尾部之后
			node.next = newNode
			newNode.pre = node

			// 新节点成为尾部
			list.tail = newNode
		} else {
			// 将新节点插入到定位到的节点之后
			// 新节点链接到定位到的节点之后
			newNode.pre = node
			node.next = newNode

			// 定位到的节点的后驱节点链接在新节点之后
			newNode.next = next
			next.pre = newNode

		}

	}

	// 列表长度+1
	list.len = list.len + 1
}

// First 返回列表链表头结点
func (list *DoubleList) First() *ListNode {
	return list.head
}

// Last 返回列表链表尾结点
func (list *DoubleList) Last() *ListNode {
	return list.tail
}

// IndexFromHead 从头部开始往后找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromHead(n int) *ListNode {
	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}

	// 获取头部节点
	node := list.head

	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}

	return node
}

// IndexFromTail 从尾部开始往前找，获取第N+1个位置的节点，索引从0开始。
func (list *DoubleList) IndexFromTail(n int) *ListNode {
	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}

	// 获取尾部节点
	node := list.tail

	// 往前遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.pre
	}

	return node
}

// PopFromHead 从头部开始往后找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromHead(n int) *ListNode {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()

	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}

	// 获取头部
	node := list.head

	// 往后遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.next
	}

	// 移除的节点的前驱和后驱
	pre := node.pre
	next := node.next

	// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
	if pre.IsNil() && next.IsNil() {
		list.head = nil
		list.tail = nil
	} else if pre.IsNil() {
		// 表示移除的是头部节点，那么下一个节点成为头节点
		list.head = next
		next.pre = nil
	} else if next.IsNil() {
		// 表示移除的是尾部节点，那么上一个节点成为尾节点
		list.tail = pre
		pre.next = nil
	} else {
		// 移除的是中间节点
		pre.next = next
		next.pre = pre
	}

	// 节点减一
	list.len = list.len - 1
	return node
}

// PopFromTail 从尾部开始往前找，获取第N+1个位置的节点，并移除返回
func (list *DoubleList) PopFromTail(n int) *ListNode {
	// 加并发锁
	list.lock.Lock()
	defer list.lock.Unlock()

	// 索引超过或等于列表长度，一定找不到，返回空指针
	if n >= list.len {
		return nil
	}

	// 获取尾部
	node := list.tail

	// 往前遍历拿到第 N+1 个位置的元素
	for i := 1; i <= n; i++ {
		node = node.pre
	}

	// 移除的节点的前驱和后驱
	pre := node.pre
	next := node.next

	// 如果前驱和后驱都为nil，那么移除的节点为链表唯一节点
	if pre.IsNil() && next.IsNil() {
		list.head = nil
		list.tail = nil
	} else if pre.IsNil() {
		// 表示移除的是头部节点，那么下一个节点成为头节点
		list.head = next
		next.pre = nil
	} else if next.IsNil() {
		// 表示移除的是尾部节点，那么上一个节点成为尾节点
		list.tail = pre
		pre.next = nil
	} else {
		// 移除的是中间节点
		pre.next = next
		next.pre = pre
	}

	// 节点减一
	list.len = list.len - 1
	return node
}

func main() {
	list := new(DoubleList)

	// 在列表头部插入新元素
	list.AddNodeFromHead(0, "I")
	list.AddNodeFromHead(0, "love")
	list.AddNodeFromHead(0, "you")
	// 在列表尾部插入新元素
	list.AddNodeFromTail(0, "may")
	list.AddNodeFromTail(0, "happy")

	list.AddNodeFromTail(list.Len()-1, "begin second")
	list.AddNodeFromHead(list.Len()-1, "end second")

	// 正常遍历，比较慢，因为内部会遍历拿到值返回
	for i := 0; i < list.Len(); i++ {
		// 从头部开始索引
		node := list.IndexFromHead(i)

		// 节点为空不可能，因为list.Len()使得索引不会越界
		if !node.IsNil() {
			fmt.Println(node.GetValue())
		}
	}

	fmt.Println("----------")

	// 正常遍历，特别快，因为直接拿到的链表节点
	// 先取出第一个元素
	first := list.First()
	for !first.IsNil() {
		// 如果非空就一直遍历
		fmt.Println(first.GetValue())
		// 接着下一个节点
		first = first.GetNext()
	}

	fmt.Println("----------")

	// 元素一个个 POP 出来
	for {
		node := list.PopFromHead(0)
		if node.IsNil() {
			// 没有元素了，直接返回
			break
		}
		fmt.Println(node.GetValue())
	}

	fmt.Println("----------")
	fmt.Println("len", list.Len())
}

输出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
you
begin second
love
I
may
end second
happy
----------
you
begin second
love
I
may
end second
happy
----------
you
begin second
love
I
may
end second
happy
----------
len 0

首先，先从列表头部插入三个新元素，然后从尾部插入两个新元素，再往头部和尾部插入两个新元素：

	list := new(DoubleList)

	// 在列表头部插入新元素
	list.AddNodeFromHead(0, "I")
	list.AddNodeFromHead(0, "love")
	list.AddNodeFromHead(0, "you")
	// 在列表尾部插入新元素
	list.AddNodeFromTail(0, "may")
	list.AddNodeFromTail(0, "happy")

	list.AddNodeFromTail(list.Len()-1, "begin second")
	list.AddNodeFromHead(list.Len()-1, "end second")

最后用三种方式进行遍历，前两种仅仅是查看元素，后一种是 PopFromHead 遍历后移除元素。

字典

我们翻阅书籍时，很多时候都要查找目录，然后定位到我们要的页数，比如我们查找某个英文单词时，会从英语字典里查看单词表目录，然后定位到词的那一页。

计算机中，也有这种需求。

一、字典

字典是存储键值对的数据结构，把一个键和一个值映射起来，一一映射，键不能重复。在某些教程中，这种结构可能称为符号表，关联数组或映射。我们暂且称它为字典，较好理解。如：

键=>值

"cat"=>2
"dog"=>1
"hen"=>3

我们拿出键 cat 的值，就是 2 了。

Golang 提供了这一数据结构：map，并且要求键的数据类型必须是可比较的，因为如果不可比较，就无法知道键是存在还是不存在。

Golang 字典的一般的操作如下：

package main

import "fmt"

func main() {
	// 新建一个容量为4的字典 map
	m := make(map[string]int64, 4)

	// 放三个键值对
	m["dog"] = 1
	m["cat"] = 2
	m["hen"] = 3

	fmt.Println(m)

	// 查找 hen
	which := "hen"
	v, ok := m[which]
	if ok {
		// 找到了
		fmt.Println("find:", which, "value:", v)
	} else {
		// 找不到
		fmt.Println("not find:", which)
	}

	// 查找 ccc
	which = "ccc"
	v, ok = m[which]
	if ok {
		// 找到了
		fmt.Println("find:", which, "value:", v)
	} else {
		// 找不到
		fmt.Println("not find:", which)
	}
}

二、实现不可重复集合 Set

一般很多编程语言库，会把不可重复集合（Collection）命名为 Set，这个 Set 中文直译为集合，在某些上下文条件下，我们大脑要自动过滤，集合这词指的是不可重复集合还是指统称的集合，在这里都可以看到中文博大精深。

不可重复集合 Set 存放数据，特点就是没有数据会重复，会去重。你放一个数据进去，再放一个数据进去，如果两个数据一样，那么只会保存一份数据。

集合 Set 可以没有顺序关系，也可以按值排序，算一种特殊的列表。

因为我们知道字典的键是不重复的，所以只要我们不考虑字典的值，就可以实现集合，我们来实现存整数的集合 Set：

// 集合结构体
type Set struct {
	m map[int]struct{} // 用字典来实现，因为字段键不能重复
	len int // 集合的大小
	sync.RWMutex  // 锁，实现并发安全
}

2.1.初始化一个集合

// 新建一个空集合
func NewSet(cap int64) *Set {
	temp := make(map[int]struct{}, cap)
	return &Set{
		m: temp,
	}
}

使用一个容量为 cap 的 map 来实现不可重复集合。map 的值我们不使用，所以值定义为空结构体 struct{}，因为空结构体不占用内存空间。如：

func main() {

	// 为什么使用空结构体
	a := struct{}{}
	b := struct{}{}
	if a == b {
		fmt.Printf("right:%p\n", &a)
	}

	fmt.Println(unsafe.Sizeof(a))
}

PS D:\Workspace\Go\src\projects\demo> go run main.go
right:0x241418
0

空结构体的内存地址都一样，并且不占用内存空间。

2.2.添加一个元素

// 增加一个元素
func (s *Set) Add(item int) {
	s.Lock()
	defer s.Unlock()
	s.m[item] = struct{}{} // 实际往字典添加这个键
	s.len = len(s.m)
}

首先，加并发锁，实现线程安全，然后往结构体 s *Set 里面的内置 map 添加该元素：item，元素作为字典的键，会自动去重。同时，集合大小重新生成。

时间复杂度等于字典设置键值对的复杂度，哈希不冲突的时间复杂度为：O(1)，否则为 O(n)，可看哈希表实现一章。

2.3.删除一个元素

// 移除一个元素
func (s *Set) Remove(item int) {
	s.Lock()
	defer s.Unlock()
	// 集合没元素直接返回
	if s.len == 0 {
		return
	}
	delete(s.m, item) // 实际从字典删除这个键
	s.len = len(s.m)  // 重新计算元素数量
}

同理，先加并发锁，然后删除 map 里面的键：item。时间复杂度等于字典删除键值对的复杂度，哈希不冲突的时间复杂度为：O(1)，否则为 O(n)，可看哈希表实现一章。

2.3.查看元素是否在集合中

// 查看是否存在元素
func (s *Set) Has(item int) bool {
	s.RLock()
	defer s.RUnlock()
	_, ok := s.m[item]
	return ok
}

时间复杂度等于字典获取键值对的复杂度，哈希不冲突的时间复杂度为：O(1)，否则为 O(n)，可看哈希表实现一章。

2.4.查看集合大小

// 查看集合大小

func (s *Set) Len() int {

    return s.len

}

时间复杂度：O(1)。

2.5.查看集合是否为空

// 集合是否为空

// 集合是否为空
func (s *Set) IsEmpty() bool {
	if s.Len() == 0 {
		return true
	}
	return false
} 

时间复杂度：O(1)。

2.6.清除集合所有元素

// 清除集合所有元素
func (s *Set) Clear() {
	s.Lock()
	defer s.Unlock()
	s.m = map[int]struct{}{} // 字典重新赋值
	s.len = 0                // 大小归零
}

将原先的 map 释放掉，并且重新赋一个空的 map。

时间复杂度：O(1)。

2.7.将集合转化为列表

func (s *Set) List() []int {
	s.RLock()
	defer s.RUnlock()
	list := make([]int, 0, s.len)
	for item := range s.m {
		list = append(list, item)
	}
	return list
}

时间复杂度：O(n)。

2.8.完例子

func main() {

	// 初始化一个容量为5的不可重复集合
	s := NewSet(5)

	s.Add(1)
	s.Add(1)
	s.Add(2)
	fmt.Println("list of all items", s.List())

	s.Clear()
	if s.IsEmpty() {
		fmt.Println("empty")
	}

	s.Add(1)
	s.Add(2)
	s.Add(3)

	if s.Has(2) {
		fmt.Println("2 does exist")
	}

	s.Remove(2)
	s.Remove(3)
	fmt.Println("list of all items", s.List())
}

PS D:\Workspace\Go\src\projects\demo> go run main.go
list of all items [1 2]
empty
2 does exist
list of all items [1]

树

树是一种比较高级的基础数据结构，由 n 个有限节点组成的具有层次关系的集合。

树的定义：

1. 有节点间的层次关系，分为父节点和子节点。
2. 有唯一一个根节点，该根节点没有父节点。
3. 除了根节点，每个节点有且只有一个父节点。
4. 每一个节点本身以及它的后代也是一棵树，是一个递归的结构。
5. 没有后代的节点称为叶子节点，没有节点的树称为空树。

二叉树：每个节点最多只有两个儿子节点的树。

满二叉树：叶子节点与叶子节点之间的高度差为 0 的二叉树，即整棵树是满的，树呈满三角形结构。在国外的定义，非叶子节点儿子都是满的树就是满二叉树。我们以国内为准。

完全二叉树：完全二叉树是由满二叉树而引出来的，设二叉树的深度为 k，除第 k 层外，其他各层的节点数都达到最大值，且第 k 层所有的节点都连续集中在最左边。

树根据儿子节点的多寡，有二叉树，三叉树，四叉树等，我们这里主要介绍二叉树。

一、二叉树的数学特征

1. 高度为 h≥0 的二叉树至少有 h+1 个结点，比如最不平衡的二叉树就是退化的线性链表结构，所有的节点都只有左儿子节点，或者所有的节点都只有右儿子节点。
2. 高度为 h≥0 的二叉树至多有 2^h+1 个节点，比如这棵树是满二叉树。
3. 含有 n≥1 个结点的二叉树的高度至多为 n-1，由 1 退化的线性链表可以反推。
4. 含有 n≥1 个结点的二叉树的高度至少为 logn，由 2 满二叉树可以反推。
5. 在二叉树的第 i 层，至多有 2^(i-1) 个节点，比如该层是满的。

二、二叉树的实现

二叉树可以使用链表来实现。如下：

// 二叉树
type TreeNode struct {
	Data  string    // 节点用来存放数据
	Left  *TreeNode // 左子树
	Right *TreeNode // 右子树
}

当然，数组也可以用来表示二叉树，一般用来表示完全二叉树。

对于一棵有 n 个节点的完全二叉树，从上到下，从左到右进行序号编号，对于任一个节点，编号 i=0 表示树根节点，编号 i 的节点的左右儿子节点编号分别为：2i+1,2i+2，父亲节点编号为：i/2，整除操作去掉小数。

如图是一棵完全二叉树，数组的表示：

我们一般使用二叉树来实现查找的功能，所以树节点结构体里存放数据的 Data 字段。

三、遍历二叉树

构建一棵树后，我们希望遍历它，有四种遍历方法：

1. 先序遍历：先访问根节点，再访问左子树，最后访问右子树。
2. 后序遍历：先访问左子树，再访问右子树，最后访问根节点。
3. 中序遍历：先访问左子树，再访问根节点，最后访问右子树。
4. 层次遍历：每一层从左到右访问每一个节点。

先序，后序和中序遍历较简单，代码如下：

package main

import "fmt"

// 二叉树
type TreeNode struct {
	Data  string    // 节点用来存放数据
	Left  *TreeNode // 左子树
	Right *TreeNode // 右子树
}

// 先序遍历
func PreOrder(tree *TreeNode) {
	if tree == nil {
		return
	}
	// 先打印根节点
	fmt.Print(tree.Data, "")
	// 再打印左子树
	PreOrder(tree.Left)
	// 再打印右字树
	PreOrder(tree.Right)
}
// 中序遍历
func MidOrder(tree *TreeNode) {
	if tree == nil {
		return
	}
	// 先打印左子树
	MidOrder(tree.Left)
	// 再打印根节点
	fmt.Print(tree.Data, "")
	// 再打印右字树
	MidOrder(tree.Right)
}
// 后序遍历
func PostOrder(tree *TreeNode) {
	if tree == nil {
		return
	}
	// 先打印左子树
	PostOrder(tree.Left)
	// 再打印右字树
	PostOrder(tree.Right)
	// 再打印根节点
	fmt.Print(tree.Data, "")
}


func main() {
	t := &TreeNode{Data: "A"}
	t.Left = &TreeNode{Data: "B"}
	t.Right = &TreeNode{Data: "C"}
	t.Left.Left = &TreeNode{Data: "D"}
	t.Left.Right = &TreeNode{Data: "E"}
	t.Right.Left = &TreeNode{Data: "F"}

	fmt.Println("先序排序：")
	PreOrder(t)
	fmt.Println("\n中序排序：")
	MidOrder(t)
	fmt.Println("\n后序排序")
	PostOrder(t)
}

表示将以下结构的树进行遍历：

PS D:\Workspace\Go\src\projects\demo> go run main.go
先序排序：
ABDECF
中序排序：
DBEAFC
后序排序
DEBFCA

层次遍历较复杂，用到一种名叫广度遍历的方法，需要使用辅助的先进先出的队列。

1. 先将树的根节点放入队列。
2. 从队列里面 remove 出节点，先打印节点值，如果该节点有左子树节点，左子树入栈，如果有右子树节点，右子树入栈。
3. 重复2，直到队列里面没有元素。

核心逻辑如下：

package main

import (
	"fmt"
	"sync"
)

// 二叉树
type TreeNode struct {
	Data  string    // 节点用来存放数据
	Left  *TreeNode // 左子树
	Right *TreeNode // 右子树
}

// 先序遍历
func PreOrder(tree *TreeNode) {
	if tree == nil {
		return
	}
	// 先打印根节点
	fmt.Print(tree.Data, "")
	// 再打印左子树
	PreOrder(tree.Left)
	// 再打印右字树
	PreOrder(tree.Right)
}

// 中序遍历
func MidOrder(tree *TreeNode) {
	if tree == nil {
		return
	}
	// 先打印左子树
	MidOrder(tree.Left)
	// 再打印根节点
	fmt.Print(tree.Data, "")
	// 再打印右字树
	MidOrder(tree.Right)
}

// 后序遍历
func PostOrder(tree *TreeNode) {
	if tree == nil {
		return
	}
	// 先打印左子树
	PostOrder(tree.Left)
	// 再打印右字树
	PostOrder(tree.Right)
	// 再打印根节点
	fmt.Print(tree.Data, "")
}
func LayerOrder(treeNode *TreeNode) {
	if treeNode == nil {
		return
	}
	// 新建队列
	queue := new(LinkQueue)
	// 根节点先入队
	queue.Add(treeNode)
	for queue.size > 0 {
		// 不断出队列
		element := queue.Remove()
		// 先打印节点值
		fmt.Print(element.Data, "")
		// 左子树非空，入队列
		if element.Left != nil {
			queue.Add(element.Left)
		}
		// 右子树非空，入队列
		if element.Right != nil {
			queue.Add(element.Right)
		}
	}
}

// 链表节点
type LinkNode struct {
	Next  *LinkNode
	Value *TreeNode
}

// 链表队列，先进先出
type LinkQueue struct {
	root *LinkNode  // 链表起点
	size int        // 队列的元素数量
	lock sync.Mutex // 为了并发安全使用的锁
}

// 入队
func (queue *LinkQueue) Add(v *TreeNode) {
	queue.lock.Lock()
	defer queue.lock.Unlock()

	// 如果栈顶为空，那么增加节点
	if queue.root == nil {
		queue.root = new(LinkNode)
		queue.root.Value = v
	} else {
		// 否则新元素插入链表的末尾
		// 新节点
		newNode := new(LinkNode)
		newNode.Value = v

		// 一直遍历到链表尾部
		nowNode := queue.root
		for nowNode.Next != nil {
			nowNode = nowNode.Next
		}

		// 新节点放在链表尾部
		nowNode.Next = newNode
	}

	// 队中元素数量+1
	queue.size = queue.size + 1
}

// 出队
func (queue *LinkQueue) Remove() *TreeNode {
	queue.lock.Lock()
	defer queue.lock.Unlock()

	// 队中元素已空
	if queue.size == 0 {
		panic("over limit")
	}

	// 顶部元素要出队
	topNode := queue.root
	v := topNode.Value

	// 将顶部元素的后继链接链上
	queue.root = topNode.Next

	// 队中元素数量-1
	queue.size = queue.size - 1

	return v
}

// 队列中元素数量
func (queue *LinkQueue) Size() int {
	return queue.size
}

func main() {
	t := &TreeNode{Data: "A"}
	t.Left = &TreeNode{Data: "B"}
	t.Right = &TreeNode{Data: "C"}
	t.Left.Left = &TreeNode{Data: "D"}
	t.Left.Right = &TreeNode{Data: "E"}
	t.Right.Left = &TreeNode{Data: "F"}
	fmt.Println("\n层次排序")
	LayerOrder(t)
}

 输出：

PS D:\Workspace\Go\src\projects\demo> go run main.go

层次排序
ABCDEF

排序算法

人类的发展中，我们学会了计数，比如知道小明今天打猎的兔子的数量是多少。另外一方面，我们也需要判断，今天哪个人打猎打得多，我们需要比较。

所以，排序这个很自然的需求就出来了。比如小明打了5只兔子，小王打了8只，还有部落其他一百多个人也打了。我们要论功行赏，谁打得多，谁就奖赏大一点。

如何排序呢，怎么在最快的时间内，找到打兔子最多的人呢，这是一个很朴素的问题。

经过很多年的研究，出现了很多的排序算法，有快的有慢的。比如：

1. 插入类排序有：直接插入排序和希尔排序
2. 选择类排序有：直接选择排序和堆排序
3. 交换类排序有：冒泡排序和快速排序

它们的复杂度如下：

稳定性概念

定义：能保证两个相等的数，经过排序之后，其在序列的前后位置顺序不变。（A1=A2，排序前A1在A2前面，排序后A1还在A2前面）

意义：稳定性本质是维持具有相同属性的数据的插入顺序，如果后面需要使用该插入顺序排序，则稳定性排序可以避免这次排序。

冒泡排序可以说是最差的排序算法。

我们把冒泡排序，直接选择排序，直接插入排序认为是初级的排序算法，其中直接插入排序的性能是综合最好的，一般来说，当排序数组规模 n 较小时，直接插入排序可能比任何排序算法都要快，建议只在小规模排序中使用。

希尔排序是对直接插入排序的改进版本，比直接选择排序和直接插入排序快，且随着规模的递增，这种性能提升越明显。因为算法容易理解，在排序数组中等规模下，我们可以使用它。在非常大的规模下，它的性能也不那么糟糕，但大规模排序还是建议使用以下的高级排序算法。

快速排序，归并排序和堆排序是比较高级的排序算法。

目前被认为综合最好的高级排序算法是快速排序，快速排序的平均用时最短，大多数的编程库内置的排序算法都是它。

堆排序也是一种很快的排序算法，通过维持一棵二叉树，树的根节点总是最大或最小从而可实现排序。

归并排序和快速排序一样使用分治法，递归地先使每个子序列有序，再将两个有序的序列进行合并成一个有序的序列。

我们在这一章将会讲解不同的排序算法。

冒泡排序

冒泡排序是大多数人学的第一种排序算法，在面试中，也是问的最多的一种，有时候还要求手写排序代码，因为比较简单。

冒泡排序属于交换类的排序算法。

一、算法介绍

现在有一堆乱序的数，比如：5 9 1 6 8 14 6 49 25 4 6 3。

第一轮迭代：从第一个数开始，依次比较相邻的两个数，如果前面一个数比后面一个数大，那么交换位置，直到处理到最后一个数，最后的这个数是最大的。

第二轮迭代：因为最后一个数已经是最大了，现在重复第一轮迭代的操作，但是只处理到倒数第二个数。

第三轮迭代：因为最后一个数已经是最大了，最后第二个数是次大的，现在重复第一轮迭代的操作，但是只处理到倒数第三个数。

第N轮迭代：....

经过交换，最后的结果为：1 3 4 5 6 6 6 8 9 14 25 49，我们可以看到已经排好序了。

因为小的元素会慢慢地浮到顶端，很像碳酸饮料的汽泡，会冒上去，所以这就是冒泡排序取名的来源。

请注意，是相邻比较两个数，也就是第一个数和第二个数比较，然后第二个数和第三个数比较...

举个简单例子，冒泡排序一个 4 个元素的数列：4 2 9 1：

[]表示排好序 {}表示比较后交换的结果

第一轮开始： 4 2 9 1 从第一个数开始，4 比 2 大，交换 4，2
第一轮： {2 4} 9 1  接着 4 比 9 小，不交换
第一轮： 2 {4 9} 1  接着 9 比 1 大，交换 9，1
第一轮： 2 4 {1 9}  已经到底，结束
第一轮结果： 2 4 1 [9] 

第二轮开始：2 4 1 [9] 从第一个数开始，2 比 4 小，不交换
第二轮： {2 4} 1 [9] 接着 4 比 1 大，交换 4，1
第二轮： 2 {1 4} [9] 已经到底，结束
第二轮结果： 2 1 [4 9] 

第三轮开始：2 1 [4 9] 从第一个数开始，2 比 1 大，交换 2，1
第三轮： (1 2} [4 9] 已经到底，结束
第三轮结果： 1 [2 4 9] 

结果： [1 2 4 9]

首先第一个数 4 和第二个数 2 比较，因为比后面的数大，所以交换，交换后第二个数为 4，然后第二个数 4 和第三个数 9 比较，因为比后面的数小，不交换，接着第三个数 9 和第四个数 1 比较，因为比后面的数大，交换，到达数列底部，第一轮结束。以此类推。

当数列的元素数量为 N，冒泡排序有两种循环，需要比较的次数为：

第一次比较的次数为： N-1 次
第二次比较的次数为： N-2 次，因为排除了最后的元素
第三次比较的次数为： N-3 次，因为排除了后两个元素
...
第某次比较的次数为：  1 次

比较次数：1 + 2 + 3 + ... + (N-1) = (N^2 - N)/2，是一个平方级别的时间复杂度，我们可以记为：O(n^2)。

交换次数：如果数列在有序的状态下进行冒泡排序，也就是最好情况下，那么交换次数为0，而如果完全乱序，最坏情况下那么交换的次数和比较的次数一样多。

冒泡排序交换和比较的次数相加是一个和 N 有关的平方数，所以冒泡排序的最好和最差时间复杂度都是：O(n^2)。

冒泡排序算法是稳定的，因为如果两个相邻元素相等，是不会交换的，保证了稳定性的要求。

我们可以改进最好的时间复杂度，使得冒泡排序最好情况的时间复杂度是 O(n)，请看下面的算法实现。

二、算法实现

package main

import "fmt"

func BubbleSort(list []int) {
	n := len(list)
	// 进行 N-1 轮迭代
	for i := n - 1; i > 0; i-- {
		// 在一轮中有没有交换过
		didSwap := false
		// 每次从第一位开始比较，比较到第 i 位就不比较了，因为前一轮该位已经有序了
		for j := 0; j < i; j++ {
			// 如果前面的数比后面的大，那么交换
			if list[j] > list[j+1] {
				list[j], list[j+1] = list[j+1], list[j]
				didSwap = true
			}
		}
		// 如果在一轮中没有交换过，那么已经排好序了，直接返回
		if !didSwap {
			return
		}
	}

}
func main() {
	list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	BubbleSort(list)
	fmt.Println(list)
}

由于切片 list 会原地排序，排序函数不需要返回任何值，处理完后可以直接打印：fmt.Println(list)。

大家还有一个疑点，很多编程语言不允许使用：list[j], list[j+1] = list[j+1], list[j] 来交换两个值，交换两个值时必须建一个临时变量 a 来作为一个过渡，如：

    a := list[j+1]
    list[j+1] = list[j]
    list[j] = a

但是 Golang 语言允许我们不那么做，它会默认构建一个临时变量来中转。

特殊说明的是：

我们引入了 didSwap 的变量，如果在一轮中该变量值没有变化，那么表示数列是有序的，所以不需要交换。也就是说在最好的情况下：对已经排好序的数列进行冒泡排序，只需比较 N 次，最好时间复杂度从 O(n^2) 骤减为 O(n)。

三、总结

冒泡排序是效率较低的排序算法，可以说是最慢的排序算法了，我们只需知道它是什么，在实际工作上切勿使用如此之慢的排序算法!

选择排序

选择排序，一般我们指的是简单选择排序，也可以叫直接选择排序，它不像冒泡排序一样相邻地交换元素，而是通过选择最小的元素，每轮迭代只需交换一次。虽然交换次数比冒泡少很多，但效率和冒泡排序一样的糟糕。

选择排序属于选择类排序算法。

我打扑克牌的时候，会习惯性地从左到右扫描，然后将最小的牌放在最左边，然后从第二张牌开始继续从左到右扫描第二小的牌，放在最小的牌右边，以此反复。选择排序和我玩扑克时的排序特别相似。

一、算法介绍

现在有一堆乱序的数，比如：5 9 1 6 8 14 6 49 25 4 6 3。

第一轮迭代，从第一个数开始，左边到右边进行扫描，找到最小的数 1，与数列里的第一个数交换位置。

第二轮迭代，从第二个数开始，左边到右边进行扫描，找到第二小的数 3，与数列里的第二个数交换位置。

第三轮迭代，从第三个数开始，左边到右边进行扫描，找到第三小的数 4，与数列里的第三个数交换位置。

第N轮迭代：....

经过交换，最后的结果为：1 3 4 5 6 6 6 8 9 14 25 49，我们可以看到已经排好序了。

注：

• 橙色表示已完成排序的元素
• 红色表示标记当前（最小/需要交换）元素
• 绿色表示扫描元素

每次扫描数列找出最小的数，然后与第一个数交换，然后排除第一个数，从第二个数开始重复这个操作，这种排序叫做简单选择排序。

举个简单例子，选择排序一个 4 个元素的数列：4 2 9 1：

[]表示排好序

起始： 4 2 9 1  未排序数列从左扫描最小的数是 1，与第一个元素 4 交换，交换 1，4
一轮： [1] 2 9 4 未排序数列从左扫描最小的数是 2，不需要交换
二轮： [1 2] 9 4 未排序数列从左扫描最小的数是 4，与第三个元素 9 交换，交换 4，9
三轮： [1 2 4] 9 未排序数列只有 1 个数，结束
结果： [1 2 4 9]

注：

• 橙色表示已完成排序的元素
• 红色表示标记当前（最小/需要交换）元素
• 绿色表示扫描元素

比较的次数和冒泡排序一样多，因为扫描过程也是比较的过程，只不过交换的次数减少为每轮 1 次。最佳和最坏时间复杂度仍然是：O(n^2)。

选择排序是一个不稳定的排序算法，比如数组：[5 6 5 1]，第一轮迭代时最小的数是 1，那么与第一个元素 5 交换位置，这样数字 1 就和数字 5 交换了位置，导致两个相同的数字 5 排序后位置变了。

二、算法实现

package main

import "fmt"

func SelectSort(list []int) {
	n := len(list)
	// 进行 N-1 轮迭代
	for i := 0; i < n-1; i++ {
		// 每次从第 i 位开始，找到最小的元素
		min := list[i] // 最小数
		minIndex := i  // 最小数的下标
		for j := i + 1; j < n; j++ {
			if list[j] < min {
				// 如果找到的数比上次的还小，那么最小的数变为它
				min = list[j]
				minIndex = j
			}
		}
		// 这一轮找到的最小数的下标不等于最开始的下标，交换元素
		if i != minIndex {
			list[i], list[minIndex] = list[minIndex], list[i]
		}
	}

}
func main() {
	list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	SelectSort(list)
	fmt.Println(list)
}

每进行一轮迭代，我们都会维持这一轮最小数：min 和最小数的下标：minIndex，然后开始扫描，如果扫描的数比该数小，那么替换掉最小数和最小数下标，扫描完后判断是否应交换，然后交换：list[i], list[minIndex] = list[minIndex], list[i]。

三、算法改进

上面的算法需要从某个数开始，一直扫描到尾部，我们可以优化算法，使得复杂度减少一半。

我们每一轮，除了找最小数之外，还找最大数，然后分别和前面和后面的元素交换，这样循环次数减少一半，如：

package main

import "fmt"

func SelectGoodSort(list []int) {
	n := len(list)
	// 只需循环一半
	for i := 0; i < n/2; i++ {
		minIndex := i // 最小值下标
		maxIndex := i // 最大值下标
		// 在这一轮迭代中要找到最大值和最小值的下标
		for j := i + 1; j < n-i; j++ {
			// 找到最大值下标
			if list[j] > list[maxIndex] {
				maxIndex = j // 这一轮这个是大的，直接 continue
				continue
			}
			// 找到最小值下标
			if list[j] < list[minIndex] {
				minIndex = j
			}
		}

		if maxIndex == i && minIndex != n-i-1 {
			// 如果最大值是开头的元素，而最小值不是最尾的元素
			// 先将最大值和最尾的元素交换
			list[n-i-1], list[maxIndex] = list[maxIndex], list[n-i-1]
			// 然后最小的元素放在最开头
			list[i], list[minIndex] = list[minIndex], list[i]
		} else if maxIndex == i && minIndex == n-i-1 {
			// 如果最大值在开头，最小值在结尾，直接交换
			list[minIndex], list[maxIndex] = list[maxIndex], list[minIndex]
		} else {
			// 否则先将最小值放在开头，再将最大值放在结尾
			list[i], list[minIndex] = list[minIndex], list[i]
			list[n-i-1], list[maxIndex] = list[maxIndex], list[n-i-1]
		}
	}

}
func main() {
	list := []int{5}
	SelectGoodSort(list)
	fmt.Println(list)

	list1 := []int{5, 9}
	SelectGoodSort(list1)
	fmt.Println(list1)

	list2 := []int{5, 9, 1}
	SelectGoodSort(list2)
	fmt.Println(list2)

	list3 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	SelectGoodSort(list3)
	fmt.Println(list3)

	list4 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6}
	SelectGoodSort(list4)
	fmt.Println(list4)
}

 PS D:\Workspace\Go\src\projects\demo> go run main.go
[5]
[5 9]
[1 5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]
[1 4 5 6 6 6 8 9 14 25 49]

优化后的选择排序还是很慢，它很好理解，但是还是不建议在工程上使用。

插入排序

插入排序，一般我们指的是简单插入排序，也可以叫直接插入排序。就是说，每次把一个数插到已经排好序的数列里面形成新的排好序的数列，以此反复。

插入排序属于插入类排序算法。

除了我以外（神奇的我），有些人打扑克时习惯从第二张牌开始，和第一张牌比较，第二张牌如果比第一张牌小那么插入到第一张牌前面，这样前两张牌都排好序了，接着从第三张牌开始，将它插入到已排好序的前两张牌里，形成三张排好序的牌，后面第四张牌继续插入到前面已排好序的三张牌里，直至排序完。

一、算法介绍

举个简单例子，有 4 个元素的数列：4 2 9 1，我们使用插入排序：

[]表示排好序

第一轮： [4] 2 9 1 拿待排序的第二个数 2，插入到排好序的数列 [4]
    与排好序的数列 [4] 比较
    第一轮进行中：2 比 4 小，插入到 4 前

第二轮： [2 4] 9 1 拿待排序的第三个数 9，插入到排好序的数列 [2 4]
    与排好序的数列 [2 4] 比较
    第二轮进行中： 9 比 4 大，不变化

第三轮： [2 4 9] 1 拿待排序的第四个数 1，插入到排好序的数列 [2 4 9]
    与排好序的数列 [2 4 9] 比较
    第三轮进行中： 1 比 9 小，插入到 9 前
    第三轮进行中： 1 比 4 小，插入到 4 前
    第三轮进行中： 1 比 2 小，插入到 2 前

结果： [1 2 4 9]

最好情况下，对一个已经排好序的数列进行插入排序，那么需要迭代 N-1 轮，并且因为每轮第一次比较，待排序的数就比它左边的数大，那么这一轮就结束了，不需要再比较了，也不需要交换，这样时间复杂度为：O(n)。

最坏情况下，每一轮比较，待排序的数都比左边排好序的所有数小，那么需要交换 N-1 次，第一轮需要比较和交换一次，第二轮需要比较和交换两次，第三轮要三次，第四轮要四次，这样次数是：1 + 2 + 3 + 4 + ... + N-1，时间复杂度和冒泡排序、选择排序一样，都是：O(n^2)。

因为是从右到左，将一个个未排序的数，插入到左边已排好序的队列中，所以插入排序，相同的数在排序后顺序不会变化，这个排序算法是稳定的。

二、算法实现

package main

import "fmt"

func InsertSort(list []int) {
	n := len(list)
	// 进行 N-1 轮迭代
	for i := 1; i <= n-1; i++ {
		deal := list[i] // 待排序的数
		j := i - 1      // 待排序的数左边的第一个数的位置

		// 如果第一次比较，比左边的已排好序的第一个数小，那么进入处理
		if deal < list[j] {
			// 一直往左边找，比待排序大的数都往后挪，腾空位给待排序插入
			for ; j >= 0 && deal < list[j]; j-- {
				list[j+1] = list[j] // 某数后移，给待排序留空位
			}
			list[j+1] = deal // 结束了，待排序的数插入空位
		}
	}
}

func main() {
	list := []int{5}
	InsertSort(list)
	fmt.Println(list)

	list1 := []int{5, 9}
	InsertSort(list1)
	fmt.Println(list1)

	list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	InsertSort(list2)
	fmt.Println(list2)
}

输出：

[5]
[5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]

其实，就是通过将右边的一个数 deal ，找到它的左边 已排好序的数列 位置，然后插进去。

数组规模 n 较小的大多数情况下，我们可以使用插入排序，它比冒泡排序，选择排序都快，甚至比任何的排序算法都快。

数列中的有序性越高，插入排序的性能越高，因为待排序数组有序性越高，插入排序比较的次数越少。

大家都很少使用冒泡、直接选择，直接插入排序算法，因为在有大量元素的无序数列下，这些算法的效率都很低。

希尔排序

1959 年一个叫 Donald L. Shell (March 1, 1924 – November 2, 2015) 的美国人在 Communications of the ACM 国际计算机学会月刊 发布了一个排序算法，从此名为希尔排序的算法诞生了。

注： ACM = Association for Computing Machinery，国际计算机学会，世界性的计算机从业员专业组织，创立于1947年，是世界上第一个科学性及教育性计算机学会。

希尔排序是直接插入排序的改进版本。因为直接插入排序对那些几乎已经排好序的数列来说，排序效率极高，达到了 O(n) 的线性复杂度，但是每次只能将数据移动一位。希尔排序创造性的可以将数据移动 n 位，然后将 n 一直缩小，缩到与直接插入排序一样为 1，请看下列分析。

希尔排序属于插入类排序算法。

一、算法介绍

有一个 N 个数的数列：

1. 先取一个小于 N 的整数 d1，将位置是 d1 整数倍的数们分成一组，对这些数进行直接插入排序。
2. 接着取一个小于 d1 的整数 d2，将位置是 d2 整数倍的数们分成一组，对这些数进行直接插入排序。
3. 接着取一个小于 d2 的整数 d3，将位置是 d3 整数倍的数们分成一组，对这些数进行直接插入排序。
4. ...
5. 直到取到的整数 d=1，接着使用直接插入排序。

这是一种分组插入方法，最后一次迭代就相当于是直接插入排序，其他迭代相当于每次移动 n 个距离的直接插入排序，这些整数是两个数之间的距离，我们称它们为增量。

我们取数列长度的一半为增量，以后每次减半，直到增量为1。

举个简单例子，希尔排序一个 12 个元素的数列：[5 9 1 6 8 14 6 49 25 4 6 3]，增量 d 的取值依次为：6，3，1：

x 表示不需要排序的数


取 d = 6 对 [5 x x x x x 6 x x x x x] 进行直接插入排序，没有变化。
取 d = 3 对 [5 x x 6 x x 6 x x 4 x x] 进行直接插入排序，排完序后：[4 x x 5 x x 6 x x 6 x x]。
取 d = 1 对 [4 9 1 5 8 14 6 49 25 6 6 3] 进行直接插入排序，因为 d=1 完全就是直接插入排序了。

越有序的数列，直接插入排序的效率越高，希尔排序通过分组使用直接插入排序，因为步长比 1 大，在一开始可以很快将无序的数列变得不那么无序，比较和交换的次数也减少，直到最后使用步长为 1 的直接插入排序，数列已经是相对有序了，所以时间复杂度会稍好一点。

在最好情况下，也就是数列是有序时，希尔排序需要进行 logn 次增量的直接插入排序，因为每次直接插入排序最佳时间复杂度都为：O(n)，因此希尔排序的最佳时间复杂度为：O(nlogn)。

在最坏情况下，每一次迭代都是最坏的，假设增量序列为： d8 d7 d6 ... d3 d2 1，那么每一轮直接插入排序的元素数量为：n/d8 n/d7 n/d6 .... n/d3 n/d2 n，那么时间复杂度按照直接插入的最坏复杂度来计算为：

假设增量序列为 ⌊N/2⌋ ，每次增量取值为比上一次的一半小的最大整数。

O( (n/d8)^2 + (n/d7)^2 + (n/d6)^2 + ... + (n/d2)^2 + n^2)

= O(1/d8^2 + 1/d7^2 + 1/d6^2 + ... + 1/d2^2 + 1) * O(n^2)
= O(等比为1/2的数列和) * O(n^2)
= O(等比求和公式) * O(n^2)
= O( (1-(1/2)^n)/(1-1/2) ) * O(n^2)
= O( (1-(1/2)^n)*2 ) * O(n^2)
= O( 2-2*(1/2)^n ) * O(n^2)
= O( < 2 ) * O(n^2)

所以，希尔排序最坏时间复杂度为 O(n^2)。

不同的分组增量序列，有不同的时间复杂度，但是没有人能够证明哪个序列是最好的。Hibbard 增量序列：1，3，7，···，2n−1 是被证明可广泛应用的分组序列，时间复杂度为：Θ(n^1.5)。

希尔排序的时间复杂度大约在这个范围：O(n^1.3)~O(n^2)，具体还无法用数学来严格证明它。

希尔排序不是稳定的，因为每一轮分组，都使用了直接插入排序，但分组会跨越 n 个位置，导致两个相同的数，发现不了对方而产生了顺序变化。

二、算法实现

package main

import "fmt"

// 增量序列折半的希尔排序
func ShellSort(list []int) {
	// 数组长度
	n := len(list)
	// 每次减半，直到步长为 1
	for step := n / 2; step >= 1; step /= 2 {
		// 开始插入排序，每一轮的步长为 step
		for i := step; i < n; i += step {
			for j := i - step; j >= 0; j -= step {
				// 满足插入那么交换元素
				if list[j+step] < list[j] {
					list[j], list[j+step] = list[j+step], list[j]
					continue
				}
				break
			}
		}
	}
}

func main() {
	list := []int{5}
	ShellSort(list)
	fmt.Println(list)

	list1 := []int{5, 9}
	ShellSort(list1)
	fmt.Println(list1)

	list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	ShellSort(list2)
	fmt.Println(list2)

	list3 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3, 2, 4, 23, 467, 85, 23, 567, 335, 677, 33, 56, 2, 5, 33, 6, 8, 3}
	ShellSort(list3)
	fmt.Println(list3)
}

[5]
[5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]
[1 2 2 3 3 4 4 5 5 6 6 6 6 8 8 9 14 23 23 25 33 33 49 56 85 335 467 567 677]

按照之前分析的几种排序算法，一般建议待排序数组为小规模情况下使用直接插入排序，在规模中等的情况下可以使用希尔排序，但在大规模还是要使用快速排序，归并排序或堆排序。

归并排序

归并排序是一种分治策略的排序算法。它是一种比较特殊的排序算法，通过递归地先使每个子序列有序，再将两个有序的序列进行合并成一个有序的序列。

归并排序首先由著名的现代计算机之父 John_von_Neumann 在 1945 年发明，被用在了 EDVAC(一台美国早期电子计算机)，足足用墨水写了 23 页的排序程序。注：冯·诺依曼（John von Neumann，1903年12月28日-1957年2月8日），美籍匈牙利数学家、计算机科学家、物理学家，是20世纪最重要的数学家之一。

一、算法介绍

我们先介绍两个有序的数组合并成一个有序数组的操作。

1. 先申请一个辅助数组，长度等于两个有序数组长度的和。
2. 从两个有序数组的第一位开始，比较两个元素，哪个数组的元素更小，那么该元素添加进辅助数组，然后该数组的元素变更为下一位，继续重复这个操作，直至数组没有元素。
3. 返回辅助数组。

举一个例子：

有序数组A：[3 8 9 11 13]
有序数组B：[1 5 8 10 17 19 20 23]
[] 表示比较的范围。

因为 1 < 3，所以 1 加入辅助数组
有序数组A：[3 8 9 11 13]
有序数组B：1 [5 8 10 17 19 20 23] 
辅助数组：1

因为 3 < 5，所以 3 加入辅助数组
有序数组A：3 [8 9 11 13]
有序数组B：1 [5 8 10 17 19 20 23] 
辅助数组：1 3

因为 5 < 8，所以 5 加入辅助数组
有序数组A：3 [8 9 11 13]
有序数组B：1 5 [8 10 17 19 20 23] 
辅助数组：1 3 5

因为 8 == 8，所以 两个数都 加入辅助数组
有序数组A：3 8 [9 11 13]
有序数组B：1 5 8 [10 17 19 20 23] 
辅助数组：1 3 5 8 8

因为 9 < 10，所以 9 加入辅助数组
有序数组A：3 8 9 [11 13]
有序数组B：1 5 8 [10 17 19 20 23] 
辅助数组：1 3 5 8 8 9

因为 10 < 11，所以 10 加入辅助数组
有序数组A：3 8 9 [11 13]
有序数组B：1 5 8 10 [17 19 20 23] 
辅助数组：1 3 5 8 8 9 10

因为 11 < 17，所以 11 加入辅助数组
有序数组A：3 8 9 11 [13]
有序数组B：1 5 8 10 [17 19 20 23] 
辅助数组：1 3 5 8 8 9 10 11

因为 13 < 17，所以 13 加入辅助数组
有序数组A：3 8 9 11 13
有序数组B：1 5 8 10 [17 19 20 23] 
辅助数组：1 3 5 8 8 9 10 11 13

因为数组A已经没有比较元素，将数组B剩下的元素拼接在辅助数组后面。

结果：1 3 5 8 8 9 10 11 13 17 19 20 23

将两个有序数组进行合并，最多进行 n 次比较就可以生成一个新的有序数组，n 是两个数组长度较大的那个。

归并操作最坏的时间复杂度为：O(n)，其中 n 是较长数组的长度。

归并操作最好的时间复杂度为：O(n)，其中 n 是较短数组的长度。

正是利用这个特点，归并排序先排序较小的数组，再将有序的小数组合并形成更大有序的数组。

归并排序有两种递归做法，一种是自顶向下，一种是自底向上。

1.1. 自顶向下归并排序

从一个大数组开始，不断地往下切分，

从上往下进行递归，直到切分的小数组无法切分了，然后不断地对这些有序数组进行合并。

每次都是一分为二，特别均匀，所以最差和最坏时间复杂度都一样。归并操作的时间复杂度为：O(n)，因此总的时间复杂度为：T(n)=2T(n/2)+O(n)，根据主定理公式可以知道时间复杂度为：O(nlogn)。我们可以自己计算一下：

归并排序，每次归并操作比较的次数为两个有序数组的长度： n/2

T(n) = 2*T(n/2) + n/2
T(n/2) = 2*T(n/4) + n/4
T(n/4) = 2*T(n/8) + n/8
T(n/8) = 2*T(n/16) + n/16
...
T(4) = 2*T(2) + 4
T(2) = 2*T(1) + 2
T(1) = 1

进行合并也就是：

T(n) = 2*T(n/2) + n/2
     = 2^2*T(n/4)+ n/2 + n/2
     = 2^3*T(n/8) + n/2 + n/2 + n/2
     = 2^4*T(n/16) + n/2 + n/2 + n/2 + n/2
     = ...
     = 2^logn*T(1) + logn * n/2
     = 2^logn + 1/2*nlogn
     = n + 1/2*nlogn

因为当问题规模 n 趋于无穷大时 nlogn 比 n 大，所以 T(n) = O(nlogn)。

因此时间复杂度为：O(nlogn)。

因为不断地递归，程序栈层数会有 logn 层，所以递归栈的空间复杂度为：O(logn)，对于排序十亿个整数，也只要：log(100 0000 0000)=29.897，占用的堆栈层数最多 30 层忧。

1.2. 自底向上归并排序

从小数组开始排序，不断地合并形成更大的有序数组。

时间复杂度和自顶向上归并排序一样，也都是 O(nlogn)。

因为不需要使用递归，没有程序栈占用，因此递归栈的空间复杂度为：O(1)。

二、算法实现

自顶向下的归并排序递归实现：

package main

import "fmt"

// 自顶向下归并排序，排序范围在 [begin,end) 的数组
func MergeSort(array []int, begin int, end int) {
	// 元素数量大于1时才进入递归\
	if end-begin > 1 {
		// 将数组一分为二，分为 array[begin,mid) 和 array[mid,high)
		mid := begin + (end-begin+1)/2

		// 先将左边排序好
		MergeSort(array, begin, mid)

		// 再将右边排序好
		MergeSort(array, mid, end)

		// 两个有序数组进行合并
		merge(array, begin, mid, end)
	}
}

// 归并操作
func merge(array []int, begin int, mid int, end int) {
	// 申请额外的空间来合并两个有序数组，这两个数组是 array[begin,mid),array[mid,end)
	leftSize := mid - begin         // 左边数组的长度
	rightSize := end - mid          // 右边数组的长度
	newSize := leftSize + rightSize // 辅助数组的长度
	result := make([]int, 0, newSize)

	l, r := 0, 0
	for l < leftSize && r < rightSize {
		lValue := array[begin+l] // 左边数组的元素
		rValue := array[mid+r]   // 右边数组的元素
		// 小的元素先放进辅助数组里
		if lValue < rValue {
			result = append(result, lValue)
			l++
		} else {
			result = append(result, rValue)
			r++
		}
	}
	// 将剩下的元素追加到辅助数组后面
	result = append(result, array[begin+l:mid]...)
	result = append(result, array[mid+r:end]...)

	// 将辅助数组的元素复制回原数组，这样该辅助空间就可以被释放掉
	for i := 0; i < newSize; i++ {
		array[begin+i] = result[i]
	}

	return

}

func main() {
	list := []int{5}
	MergeSort(list, 0, len(list))
	fmt.Println(list)

	list1 := []int{5, 9}
	MergeSort(list1, 0, len(list1))
	fmt.Println(list1)

	list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	MergeSort(list2, 0, len(list2))
	fmt.Println(list2)
}

输出：

[5]
[5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]

自顶向下递归排序，我们可以看到每次合并都要申请一个辅助数组，然后合并完再赋值回原数组，这样每次合并后辅助数组的内存就可以释放掉，存储空间占用 n，而程序递归栈依旧是 logn 层。

自底向上的非递归实现：

package main

import "fmt"

// 自底向上归并排序
func MergeSort2(array []int, begin int, end int) {
	// 步数为1开始，step长度的数组表示一个有序的数组
	step := 1
	// 范围大于 step 的数组才可以进入归并
	if end-begin > step {
		// 从头到尾对数组进行归并操作
		// step << 1 = 2 * step 表示偏移到后两个有序数组将它们进行归并
		for i := begin; i < end; i += step << 1 {
			var lo = i                // 第一个有序数组的上界
			var mid = lo + step       // 第一个有序数组的下界，第二个有序数组的上界
			var hi = lo + (step << 1) // 第二个有序数组的下界
			// 不存在第二个数组，直接返回
			if mid > end {
				return
			}
			// 第二个数组长度不够
			if hi > end {
				hi = end
			}
			// 两个有序数组进行合并
			merge(array, lo, mid, hi)
		}
		// 上面的 step 长度的两个数组都归并成一个数组了，现在步长翻倍
		step <<= 1
	}
}

// 归并操作
func merge(array []int, begin int, mid int, end int) {
	// 申请额外的空间来合并两个有序数组，这两个数组是 array[begin,mid),array[mid,end)
	leftSize := mid - begin         // 左边数组的长度
	rightSize := end - mid          // 右边数组的长度
	newSize := leftSize + rightSize // 辅助数组的长度
	result := make([]int, 0, newSize)

	l, r := 0, 0
	for l < leftSize && r < rightSize {
		lValue := array[begin+l] // 左边数组的元素
		rValue := array[mid+r]   // 右边数组的元素
		// 小的元素先放进辅助数组里
		if lValue < rValue {
			result = append(result, lValue)
			l++
		} else {
			result = append(result, rValue)
			r++
		}
	}
	// 将剩下的元素追加到辅助数组后面
	result = append(result, array[begin+l:mid]...)
	result = append(result, array[mid+r:end]...)

	// 将辅助数组的元素复制回原数组，这样该辅助空间就可以被释放掉
	for i := 0; i < newSize; i++ {
		array[begin+i] = result[i]
	}

	return

}

func main() {
	list := []int{5}
	MergeSort2(list, 0, len(list))
	fmt.Println(list)

	list1 := []int{5, 9}
	MergeSort2(list1, 0, len(list1))
	fmt.Println(list1)

	list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	MergeSort2(list2, 0, len(list2))
	fmt.Println(list2)
}

输出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
[5]
[5 9]
[5 9 1 6 8 14 6 49 4 25 3 6]

自底向上非递归排序，我们可以看到没有递归那样程序栈的增加，效率比自顶向上的递归版本高

三、算法改进

归并排序归并操作占用了额外的辅助数组，且归并操作是从一个元素的数组开始。

我们可以做两点改进：

1. 对于小规模数组，使用直接插入排序。
2. 原地排序，节约掉辅助数组空间的占用。

我们建议使用自底向上非递归排序，不会有程序栈空间损耗。

我们先来介绍一种翻转算法，也叫手摇算法，主要用来对数组两部分进行位置互换，比如数组： [9,8,7,1,2,3]，将前三个元素与后面的三个元素交换位置，变成 [1,2,3,9,8,7]。

再比如，将字符串 abcde1234567 的前 5 个字符与后面的字符交换位置，那么手摇后变成：1234567abcde。

如何翻转呢？

1. 将前部分逆序
2. 将后部分逆序
3. 对整体逆序

示例如下：

翻转 [1234567abcde] 的前5个字符。

1. 分成两部分：[abcde][1234567]
2. 分别逆序变成：[edcba][7654321]
3. 整体逆序：[1234567abcde]

归并原地排序利用了手摇算法的特征，不需要额外的辅助数组。

首先，两个有序的数组，分别是 arr[begin,mid-1]，arr[mid,end]，此时初始化 i=begin，j=mid，k=end，从 i~j 为左有序的数组，k~j为右有序的数组，

将 i 向后移动，找到第一个 arr[i]>arr[j]的索引，这个时候，i 前面的部分已经排好序了，begin~i 这些元素已经是两个有序数组的前 n 小个元素。'

然后将 j 向后移动，找到第一个 arr[j]>arr[i]的索引，

这个时候，mid~j 中的元素都小于 arr[i]，前面已经知道从 begin~i 已经是前 n 小了，所以这两部分 begin~i，mid~j 也是有序的了，我们要想办法将这两部分连接在一起。

我们只需进行翻转，将 i~mid 和 mid,j-1 部分进行位置互换即可，我们可以用手摇算法。

具体的代码如下：

package main

import "fmt"

func InsertSort(list []int) {
	n := len(list)
	// 进行 N-1 轮迭代
	for i := 1; i <= n-1; i++ {
		deal := list[i] // 待排序的数
		j := i - 1      // 待排序的数左边的第一个数的位置

		// 如果第一次比较，比左边的已排好序的第一个数小，那么进入处理
		if deal < list[j] {
			// 一直往左边找，比待排序大的数都往后挪，腾空位给待排序插入
			for ; j >= 0 && deal < list[j]; j-- {
				list[j+1] = list[j] // 某数后移，给待排序留空位
			}
			list[j+1] = deal // 结束了，待排序的数插入空位
		}
	}
}

// 自底向上归并排序优化版本
func MergeSort3(array []int, n int) {
	// 按照三个元素为一组进行小数组排序，使用直接插入排序
	blockSize := 3
	a, b := 0, blockSize
	for b <= n {
		InsertSort(array[a:b])
		a = b
		b += blockSize
	}
	InsertSort(array[a:n])

	// 将这些小数组进行归并
	for blockSize < n {
		a, b = 0, 2*blockSize
		for b <= n {
			merge(array, a, a+blockSize, b)
			a = b
			b += 2 * blockSize
		}
		if m := a + blockSize; m < n {
			merge(array, a, m, n)
		}
		blockSize *= 2
	}
}

// 原地归并操作
func merge(array []int, begin, mid, end int) {
	// 三个下标，将数组 array[begin,mid] 和 array[mid,end-1]进行原地归并
	i, j, k := begin, mid, end-1 // 因为数组下标从0开始，所以 k = end-1

	for j-i > 0 && k-j >= 0 {
		step := 0
		// 从 i 向右移动，找到第一个 array[i]>array[j]的索引
		for j-i > 0 && array[i] <= array[j] {
			i++
		}

		// 从 j 向右移动，找到第一个 array[j]>array[i]的索引
		for k-j >= 0 && array[j] <= array[i] {
			j++
			step++
		}

		// 进行手摇翻转，将 array[i,mid] 和 [mid,j-1] 进行位置互换
		// mid 是从 j 开始向右出发的，所以 mid = j-step
		rotation(array, i, j-step, j-1)
		i = i + step
	}

}

// 手摇算法，将 array[l,l+1,l+2,...,mid-2,mid-1,mid,mid+1,mid+2,...,r-2,r-1,r] 从mid开始两边交换位置
// 1.先逆序前部分：array[mid-1,mid-2,...,l+2,l+1,l]
// 2.后逆序后部分：array[r,r-1,r-2,...,mid+2,mid+1,mid]
// 3.上两步完成后：array[mid-1,mid-2,...,l+2,l+1,l,r,r-1,r-2,...,mid+2,mid+1,mid]
// 4.整体逆序： array[mid,mid+1,mid+2,...,r-2,r-1,r,l,l+1,l+2,...,mid-2,mid-1]
func rotation(array []int, l, mid, r int) {
	reverse(array, l, mid-1)
	reverse(array, mid, r)
	reverse(array, l, r)
}

func reverse(array []int, l, r int) {
	for l < r {
		// 左右互相交换
		array[l], array[r] = array[r], array[l]
		l++
		r--
	}
}

func main() {
	list := []int{5}
	MergeSort3(list, len(list))
	fmt.Println(list)

	list1 := []int{5, 9}
	MergeSort3(list1, len(list1))
	fmt.Println(list1)

	list2 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	MergeSort3(list2, len(list2))
	fmt.Println(list2)

	list3 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3, 45, 67, 2, 5, 24, 56, 34, 24, 56, 2, 2, 21, 4, 1, 4, 7, 9}
	MergeSort3(list3, len(list3))
	fmt.Println(list3)
}

输出：

[5]
[5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]
[1 1 2 2 2 3 4 4 4 5 5 6 6 6 7 8 9 9 14 21 24 24 25 34 45 49 56 56 67]

我们自底开始，将元素按照数量为 blockSize 进行小数组排序，使用直接插入排序，然后我们对这些有序的数组向上进行归并操作。

归并过程中，使用原地归并，用了手摇算法，代码如下：

func rotation(array []int, l, mid, r int) {
	reverse(array, l, mid-1)
	reverse(array, mid, r)
	reverse(array, l, r)
}

因为手摇只多了逆序翻转的操作，时间复杂度是 O(n)，虽然时间复杂度稍稍多了一点，但存储空间复杂度降为了 O(1)。

归并排序是唯一一个有稳定性保证的高级排序算法，某些时候，为了寻求大规模数据下排序前后，相同元素位置不变，可以使用归并排序。

优先队列及堆排序

堆排序( Heap Sort )由威尔士-加拿大计算机科学家 J. W. J. Williams 在 1964 年发明，它利用了二叉堆 (A binary heap) 的性质实现了排序，并证明了二叉堆数据结构的可用性。同年，美国籍计算机科学家 R. W. Floyd 在其树排序研究的基础上，发布了一个改进的更好的原地排序的堆排序版本。

堆排序属于选择类排序算法。

一、优先队列

优先队列是一种能完成以下任务的队列：插入一个数值，取出最小或最大的数值（获取数值，并且删除）。

优先队列可以用二叉树来实现，我们称这种结构为二叉堆。

最小堆和最大堆是二叉堆的一种，是一棵完全二叉树（一种平衡树）。

最小堆的性质：

1. 父节点的值都小于左右儿子节点。
2. 这是一个递归的性质。

最大堆的性质：

1. 父节点的值都大于左右儿子节点。
2. 这是一个递归的性质。

最大堆和最小堆实现方式一样，只不过根节点一个是最大的，一个是最小的。

1.1. 最大堆特征

最大堆实现细节(两个操作)：

1. push：向堆中插入数据时，首先在堆的末尾插入数据，如果该数据比父亲节点还大，那么交换，然后不断向上提升，直到没有大小颠倒为止。
2. pop：从堆中删除最大值时，首先把最后一个值复制到根节点上，并且删除最后一个数值，然后和儿子节点比较，如果值小于儿子，与儿子节点交换，然后不断向下交换， 直到没有大小颠倒为止。在向下交换过程中，如果有两个子儿子都大于自己，就选择较大的。

最大堆有两个核心操作，一个是上浮，一个是下沉，分别对应 push 和 pop。

这是一个最大堆：用数组表示为：[11 5 8 3 4]

1.2. 上浮操作

我们要往堆里 push 一个元素 15，我们先把 X = 15 放到树最尾部，然后进行上浮操作。

因为 15 大于其父亲节点 8，所以与父亲替换：

这时 15 还是大于其父亲节点 11，继续替换：

操作一次 push 的最好时间复杂度为：O(1)，因为第一次上浮时如果不大于父亲，那么就结束了。最坏的时间复杂度为： O(logn)，相当于每次都大于父亲，会一直往上浮到根节点，翻转次数等于树的高度，而树的高度等于元素个数的对数：log(n)。

1.3. 下沉操作

我们现在要将堆顶的元素 pop 出。如图我们要移除最大的元素 11：

我们先将根节点移除，然后将最尾部的节点 4 放在根节点上：

接着对根节点 4 进行下沉操作，与其两个儿子节点比较，发现较大的儿子节点 8 比 4 大，那么根节点 4 与其儿子节点 8 交换位置，向下翻转：

这样一直向下翻转就维持了最大堆的特征。

操作一次 pop 最好的时间复杂度也是：O(1)，因为第一次比较时根节点就是最大的。最坏时间复杂度仍然是树的高度：O(logn)。

1.4. 时间复杂度分析

构建一个最大堆，从空堆开始，每次添加元素到尾部后，需要向上翻转，最坏翻转次数是：

第一次添加元素翻转次数：log1
第二次添加元素翻转次数：log2
第三次添加元素翻转次数：不大于log3的最大整数
第四次添加元素翻转次数：log4
第五次添加元素翻转次数：不大于log5的最大整数
...
第N次添加元素翻转次数：不大于logn的最大整数

近似 = log(1)+log(2)+log(3)+...+log(n) = log(n!)

从一个最大堆，逐一移除堆顶元素，然后将堆尾元素置于堆顶后，向下翻转恢复堆特征，最坏翻转次数是:

第一次移除元素恢复堆时间复杂度：logn
第二次移除元素恢复堆时间复杂度：不大于log(n-1)的最大整数
第三次移除元素恢复堆时间复杂度：不大于log(n-2)的最大整数
...
第N次移除元素恢复堆时间复杂度：log1

近似 = log(1)+log(2)+log(3)+...+log(n) = log(n!)

根据斯特林公式：

可以进行证明 log(n!) 和 nlog(n) 是同阶的：

所以构建一个最大堆的最坏时间复杂度是：O(nlogn)。

从堆顶一个个移除元素，直到移完，整个过程最坏时间复杂度也是：O(nlogn)。

从构建堆到移除堆，总的最坏复杂度是：O(nlogn)+O(nlogn)，我们可以认为是：O(nlogn)。

如果所有的元素都一样的情况下，建堆和移除堆的每一步都不需要翻转，最好时间复杂度为：O(n)，复杂度主要在于遍历元素。

如果元素不全一样，即使在建堆的时候不需要翻转，但在移除堆的过程中一定会破坏堆的特征，导致恢复堆时需要翻转。比如一个 n 个元素的已排好的序的数列，建堆时每次都满足堆的特征，不需要上浮翻转，但在移除堆的过程中最尾部元素需要放在根节点，这个时候导致不满足堆的特征，需要下沉翻转。因此，在最好情况下，时间复杂度仍然是：O(nlog)。

因此，最大堆从构建到移除，总的平均时间复杂度是：O(nlogn)。

1.5. 最大堆实现

// 一个最大堆，一棵完全二叉树
// 最大堆要求节点元素都不小于其左右孩子
type Heap struct {
	// 堆的大小
	Size int
	// 使用内部的数组来模拟树
	// 一个节点下标为 i，那么父亲节点的下标为 (i-1)/2
	// 一个节点下标为 i，那么左儿子的下标为 2i+1，右儿子下标为 2i+2
	Array []int
}

// 初始化一个堆
func NewHeap(array []int) *Heap {
	h := new(Heap)
	h.Array = array
	return h
}
// 最大堆插入元素
func (h *Heap) Push(x int) {
	// 堆没有元素时，使元素成为顶点后退出
	if h.Size == 0 {
		h.Array[0] = x
		h.Size++
		return
	}
	// i 是要插入节点的下标
	i := h.Size
	// 如果下标存在
	// 将小的值 x 一直上浮
	for i > 0 {
		// parent为该元素父亲节点的下标
		parent := (i-1)/2
		// 如果插入的值小于等于父亲节点，那么可以直接退出循环，因为父亲仍然是最大的
		if x <= h.Array[parent] {
			break
		}
		// 否则将父亲节点与该节点互换，然后向上翻转，将最大的元素一直往上推
		h.Array[i] = h.Array[parent]
		i = parent
	}
	// 将该值 x 放在不会再翻转的位置
	h.Array[i] = x
	// 堆数量加一
	h.Size++
}
// 最大堆移除根节点元素，也就是最大的元素
func (h *Heap) Pop() int {
	// 没有元素，返回-1
	if h.Size == 0 {
		return -1
	}
	// 取出根节点
	ret := h.Array[0]
	// 因为根节点要被删除了，将最后一个节点放到根节点的位置上
	h.Size--
	x := h.Array[h.Size] // 将最后一个元素的值先拿出来
	h.Array[h.Size] = ret // 将移除的元素放在最后一个元素的位置上

	// 对根节点进行向下翻转，小的值 x 一直下沉，维持最大堆的特征
	i := 0
	for {
		// a，b为下标 i 左右两个子节点的下标
		a := 2*i +1
		b := 2*i +2
		// 左儿子下标超出了，表示没有左子树，那么右子树也没有，直接返回
		if a >= h.Size {
			break
		}
		// 有右子树，拿到两个子节点中较大节点的下标
		if b < h.Size && h.Array[b] > h.Array[a] {
			a = b
		}

		// 父亲节点的值都大于或等于两个儿子较大的那个，不需要向下继续翻转了，返回
		if x >= h.Array[a] {
			break
		}
		// 将较大的儿子与父亲交换，维持这个最大堆的特征
		h.Array[i] = h.Array[a]
		// 继续往下操作
		i = a
	}
	// 将最后一个元素的值 x 放在不会再翻转的位置
	h.Array[i] = x
	return ret
}

以上为最大堆的实现。

三、普通堆排序

根据最大堆，堆顶元

素一直是最大的元素特征，可以实现堆排序。

先构建一个最大堆，然后依次把根节点元素 pop 出即可：

func main() {
	list := []int{5,9,1,6,8,14,6,49,25,4,6,3}
	// 构建最大堆
	h := NewHeap(list)
	for _, v := range list {
		h.Push(v)
	}
	// 将堆元素移除
	for range list {
		h.Pop()
	}
	// 打印排序后的值
	fmt.Println(list)
}

输出：

1 3 4 5 6 6 6 8 9 14 25 49 

根据以上最大堆的时间复杂度分析，从堆构建到移除最坏和最好的时间复杂度：O(nlogn)，这也是堆排序的最好和最坏的时间复杂度。

这样实现的堆排序是普通的堆排序，性能不是最优的。

因为一开始会认为堆是空的，每次添加元素都需要添加到尾部，然后向上翻转，需要用 Heap.Size 来记录堆的大小增长，这种堆构建，可以认为是非原地的构建，影响了效率。

美国籍计算机科学家 R. W. Floyd 改进的原地自底向上的堆排序，不会从空堆开始，而是把待排序的数列当成一个混乱的最大堆，从底层逐层开始，对元素进行下沉操作，一直恢复最大堆的特征，直到根节点。

将构建堆的时间复杂度从 O(nlogn) 降为 O(n)，总的堆排序时间复杂度从 O(2nlogn) 改进到 O(n+nlogn)。

三、自底向上堆排序

自底向上堆排序，仅仅将构建堆的时间复杂度从 O(nlogn) 改进到 O(n)，其他保持不变。

这种堆排序，不再每次都将元素添加到尾部，然后上浮翻转，而是在混乱堆的基础上，从底部向上逐层进行下沉操作，下沉操作比较的次数会减少。步骤如下：

1. 先对最底部的所有非叶子节点进行下沉，即这些非叶子节点与它们的儿子节点比较，较大的儿子和父亲交换位置。
2. 接着从次二层开始的非叶子节点重复这个操作，直到到达根节点最大堆就构建好了。

从底部开始，向上推进，所以这种堆排序又叫自底向上的堆排序。

为什么自底向上构建堆的时间复杂度是：O(n)。证明如下：

第 k 层的非叶子节点的数量为 n/2^k，每一个非叶子节点下沉的最大次数为其子孙的层数：k，而树的层数为 logn 层，那么总的翻转次数计算如下：因为如下的公式是成立的：

所以翻转的次数计算结果为：2n 次。也就是构建堆的时间复杂度为：O(n)。

我们用非递归的形式来实现，非递归相对容易理解：

package main

import "fmt"

// 一个最大堆，一棵完全二叉树
// 最大堆要求节点元素都不小于其左右孩子
type Heap struct {
	// 堆的大小
	Size int
	// 使用内部的数组来模拟树
	// 一个节点下标为 i，那么父亲节点的下标为 (i-1)/2
	// 一个节点下标为 i，那么左儿子的下标为 2i+1，右儿子下标为 2i+2
	Array []int
}

// 初始化一个堆
func NewHeap(array []int) *Heap {
	h := new(Heap)
	h.Array = array
	return h
}

// 最大堆插入元素
func (h *Heap) Push(x int) {
	// 堆没有元素时，使元素成为顶点后退出
	if h.Size == 0 {
		h.Array[0] = x
		h.Size++
		return
	}
	// i 是要插入节点的下标
	i := h.Size
	// 如果下标存在
	// 将小的值 x 一直上浮
	for i > 0 {
		// parent为该元素父亲节点的下标
		parent := (i - 1) / 2
		// 如果插入的值小于等于父亲节点，那么可以直接退出循环，因为父亲仍然是最大的
		if x <= h.Array[parent] {
			break
		}
		// 否则将父亲节点与该节点互换，然后向上翻转，将最大的元素一直往上推
		h.Array[i] = h.Array[parent]
		i = parent
	}
	// 将该值 x 放在不会再翻转的位置
	h.Array[i] = x
	// 堆数量加一
	h.Size++
}

// 最大堆移除根节点元素，也就是最大的元素
func (h *Heap) Pop() int {
	// 没有元素，返回-1
	if h.Size == 0 {
		return -1
	}
	// 取出根节点
	ret := h.Array[0]
	// 因为根节点要被删除了，将最后一个节点放到根节点的位置上
	h.Size--
	x := h.Array[h.Size]  // 将最后一个元素的值先拿出来
	h.Array[h.Size] = ret // 将移除的元素放在最后一个元素的位置上

	// 对根节点进行向下翻转，小的值 x 一直下沉，维持最大堆的特征
	i := 0
	for {
		// a，b为下标 i 左右两个子节点的下标
		a := 2*i + 1
		b := 2*i + 2
		// 左儿子下标超出了，表示没有左子树，那么右子树也没有，直接返回
		if a >= h.Size {
			break
		}
		// 有右子树，拿到两个子节点中较大节点的下标
		if b < h.Size && h.Array[b] > h.Array[a] {
			a = b
		}

		// 父亲节点的值都大于或等于两个儿子较大的那个，不需要向下继续翻转了，返回
		if x >= h.Array[a] {
			break
		}
		// 将较大的儿子与父亲交换，维持这个最大堆的特征
		h.Array[i] = h.Array[a]
		// 继续往下操作
		i = a
	}
	// 将最后一个元素的值 x 放在不会再翻转的位置
	h.Array[i] = x
	return ret
}

// 先自底向上构建最大堆，再移除堆元素实现堆排序
func HeapSort(array []int) {
	// 堆的元素数量
	count := len(array)

	// 最底层的叶子节点下标，该节点位置不定，但是该叶子节点右边的节点都是叶子节点
	start := count/2 + 1
	// 最后的元素下标
	end := count - 1
	// 从最底层开始，逐一对节点进行下沉

	for start >= 0 {
		sift(array, start, count)
		start-- // 表示左偏移一个节点，如果该层没有节点了，那么表示到了上一层的最右边
	}
	// 下沉结束了，现在要来排序了
	// 元素大于2个的最大堆才可以移除
	for end > 0 {
		// 将堆顶元素与堆尾元素互换，表示移除最大堆元素
		array[end], array[0] = array[0], array[end]
		// 对堆顶进行下沉操作
		sift(array, 0, end)
		// 一直移除堆顶元素
		end--
	}
}

// 下沉操作，需要下沉的元素时 array[start]，参数 count 只要用来判断是否到底堆底，使得下沉结束
func sift(array []int, start, count int) {
	// 父亲节点
	root := start
	// 左儿子
	child := root*2 + 1
	// 如果有下一代
	for child < count {
		// 右儿子比左儿子大，那么要翻转的儿子改为右儿子
		if count-child > 1 && array[child] < array[child+1] {
			child++
		}
		// 父亲节点比儿子小，那么将父亲和儿子位置交换
		if array[root] < array[child] {
			array[root], array[child] = array[child], array[root]
			// 继续往下沉
			root = child
			child = root*2 + 1
		} else {
			return
		}
	}
}
func main() {
	list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}

	HeapSort(list)

	// 打印排序后的值
	fmt.Println(list)
}

输出：

[1 3 4 5 6 6 6 8 9 14 25 49]

快速排序

快速排序是一种分治策略的排序算法，是由英国计算机科学家 Tony Hoare 发明的， 该算法被发布在 1961 年的 Communications of the ACM 国际计算机学会月刊。

注： ACM = Association for Computing Machinery，国际计算机学会，世界性的计算机从业员专业组织，创立于1947年，是世界上第一个科学性及教育性计算机学会。

本质上来看，快速排序是对冒泡排序的一种改进，属于交换类的排序算法。

一、算法介绍

快速排序通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤如下：

1. 先从数列中取出一个数作为基准数。一般取第一个数。
2. 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3. 再对左右区间重复第二步，直到各区间只有一个数。

举一个例子：5 9 1 6 8 14 6 49 25 4 6 3。

一般取第一个数 5 作为基准，从它左边和最后一个数使用[]进行标志，

如果左边的数比基准数大，那么该数要往右边扔，也就是两个[]数交换，这样大于它的数就在右边了，然后右边[]数左移，否则左边[]数右移。

5 [9] 1 6 8 14 6 49 25 4 6 [3]  因为 9 > 5，两个[]交换位置后，右边[]左移
5 [3] 1 6 8 14 6 49 25 4 [6] 9  因为 3 !> 5，两个[]不需要交换，左边[]右移
5 3 [1] 6 8 14 6 49 25 4 [6] 9  因为 1 !> 5，两个[]不需要交换，左边[]右移
5 3 1 [6] 8 14 6 49 25 4 [6] 9  因为 6 > 5，两个[]交换位置后，右边[]左移
5 3 1 [6] 8 14 6 49 25 [4] 6 9  因为 6 > 5，两个[]交换位置后，右边[]左移
5 3 1 [4] 8 14 6 49 [25] 6 6 9  因为 4 !> 5，两个[]不需要交换，左边[]右移
5 3 1 4 [8] 14 6 49 [25] 6 6 9  因为 8 > 5，两个[]交换位置后，右边[]左移
5 3 1 4 [25] 14 6 [49] 8 6 6 9  因为 25 > 5，两个[]交换位置后，右边[]左移
5 3 1 4 [49] 14 [6] 25 8 6 6 9  因为 49 > 5，两个[]交换位置后，右边[]左移
5 3 1 4 [6] [14] 49 25 8 6 6 9  因为 6 > 5，两个[]交换位置后，右边[]左移
5 3 1 4 [14] 6 49 25 8 6 6 9  两个[]已经汇总，因为 14 > 5，所以 5 和[]之前的数 4 交换位置
第一轮切分结果：4 3 1 5 14 6 49 25 8 6 6 9  

现在第一轮快速排序已经将数列分成两个部分：

4 3 1 和 14 6 49 25 8 6 6 9

左边的数列都小于 5，右边的数列都大于 5。

使用递归分别对两个数列进行快速排序。

注：

• 黄色是基准数
• 橙色是已经排序完成的元素
• 紫色是大于基准数的元素
• 绿色是小于基准数的元素
• 红色是正在与基准数进行比较的元素

快速排序主要靠基准数进行切分，将数列分成两部分，一部分比基准数都小，一部分比基准数都大。

1.1 时间复杂度

在最好情况下，每一轮都能平均切分，每一轮遍历比较元素 n 次就可以把数列分成两部分，每一轮的时间复杂度都是：O(n)。因为问题规模每次被折半，折半的数列继续递归进行切分，也就是总的时间复杂度计算公式为： T(n) = 2*T(n/2) + O(n)。按照主定理公式计算，我们可以知道时间复杂度为：O(nlogn)，当然我们可以来具体计算一下：

我们来分析最好情况，每一轮切分，遍历比较元素的次数为 n

T(n) = 2*T(n/2) + n
T(n/2) = 2*T(n/4) + n/2
T(n/4) = 2*T(n/8) + n/4
T(n/8) = 2*T(n/16) + n/8
...
T(4) = 2*T(2) + 4
T(2) = 2*T(1) + 2
T(1) = 1

进行合并也就是：

T(n) = 2*T(n/2) + n
     = 2^2*T(n/4)+ n + n
     = 2^3*T(n/8) + n + n + n
     = 2^4*T(n/16) + n + n + n + n
     = ...
     = 2^logn*T(1) + logn * n
     = 2^logn + nlogn
     = n + nlogn

因为当问题规模 n 趋于无穷大时 nlogn 比 n 大，所以 T(n) = O(nlogn)。

最好时间复杂度为：O(nlogn)。

注：^ 表示乘方。

最差的情况下，每次都不能平均地切分，每次切分都因为基准数是最大的或者最小的，不能分成两个数列，这样时间复杂度变为了 T(n) = T(n-1) + O(n)，按照主定理计算可以知道时间复杂度为：O(n^2)，我们可以来实际计算一下：

我们来分析最差情况，每一轮切分，遍历比较元素的次数为 n

T(n) = T(n-1) + n
     = T(n-2) + n-1 + n
     = T(n-3) + n-2 + n-1 + n
     = ...
     = T(1) + 2 +3 + ... + n-2 + n-1 + n
     = O(n^2)

最差时间复杂度为：O(n^2)。

注：^ 表示乘方。

根据熵的概念，数量越大，随机性越高，越自发无序，所以待排序数据规模非常大时，出现最差情况的情形较少。在综合情况下，快速排序的平均时间复杂度为：O(nlogn)。对比之前介绍的排序算法，快速排序比那些动不动就是平方级别的初级排序算法更佳。

1.2 空间复杂度

快速排序使用原地排序，存储空间复杂度为：O(1)。而因为递归栈的影响，递归的程序栈开辟的层数范围在 logn ~ n，所以递归栈的空间复杂度为：O(logn) ~ log(n)，最坏为：log(n)，当元素较多时，程序栈可能溢出。通过改进算法，使用伪尾递归进行优化，递归栈的空间复杂度可以减小到 O(logn)，可以见下面算法优化。

快速排序是不稳定的，因为切分过程中进行了交换，相同值的元素可能发生位置变化。

1.3 切分优化

切分的结果极大地影响快速排序的性能，比如每次切分的时候选择的基数数都是数组中最大或者最小的，会出现最坏情况，为了避免切分不均匀情况的发生，有几种方法改进：

1. 随机基准数选择：每次进行快速排序切分时，先将数列随机打乱，再进行切分，这样随机加了个震荡，减少不均匀的情况。当然，也可以随机选择一个基准数，而不是选第一个数。
2. 中位数选择：每次取数列头部，中部，尾部三个数，取三个数的中位数为基准数进行切分。

方法 1 相对好，而方法 2 引入了额外的比较操作，一般情况下我们可以随机选择一个基准数。

从一个数组中随机选择一个数，或者取中位数都比较容易实现，我们在此就不实现了，避免造成心智负担，下文代码实现都取第一个数为基准数。

二、算法实现

这是最普通的一种实现。

package main

import "fmt"

// QuickSort 普通快速排序
func QuickSort(array []int, begin, end int) {
	if begin < end {
		// 进行切分
		loc := partition(array, begin, end)
		// 对左部分进行快排
		QuickSort(array, begin, loc-1)
		// 对右部分进行快排
		QuickSort(array, loc+1, end)
	}
}

// 切分函数，并返回切分元素的下标
func partition(array []int, begin, end int) int {
	i := begin + 1 // 将array[begin]作为基准数，因此从array[begin+1]开始与基准数比较！
	j := end       // array[end]是数组的最后一位
	// 没重合之前
	for i < j {
		if array[i] > array[begin] {
			array[i], array[j] = array[j], array[i] // 交换
			j--
		} else {
			i++
		}
	}
	/* 跳出 for 循环后，i = j。
	 * 此时数组被分割成两个部分   -->  array[begin+1] ~ array[i-1] < array[begin]
	 *                        -->  array[i+1] ~ array[end] > array[begin]
	 * 这个时候将数组array分成两个部分，再将array[i]与array[begin]进行比较，决定array[i]的位置。
	 * 最后将array[i]与array[begin]交换，进行两个分割部分的排序！以此类推，直到最后i = j不满足条件就退出！
	 */
	if array[i] >= array[begin] { // 这里必须要取等“>=”，否则数组元素由相同的值组成时，会出现错误！
		i--
	}
	array[begin], array[i] = array[i], array[begin]
	return i
}

func main() {
	list := []int{5}
	QuickSort(list, 0, len(list)-1)
	fmt.Println(list)

	list1 := []int{5, 9}
	QuickSort(list1, 0, len(list1)-1)
	fmt.Println(list1)

	list2 := []int{5, 9, 1}
	QuickSort(list2, 0, len(list2)-1)
	fmt.Println(list2)

	list3 := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
	QuickSort(list3, 0, len(list3)-1)
	fmt.Println(list3)
}

输出：

[5]
[5 9]
[1 5 9]
[1 3 4 5 6 6 6 8 9 14 25 49]

示例图：

快速排序，每一次切分都维护两个下标，进行推进，最后将数列分成两部分。

三、算法改进

快速排序可以继续进行算法改进。

1. 在小规模数组的情况下，直接插入排序的效率最好，当快速排序递归部分进入小数组范围，可以切换成直接插入排序。
2. 排序数列可能存在大量重复值，使用三向切分快速排序，将数组分成三部分，大于基准数，等于基准数，小于基准数，这个时候需要维护三个下标。
3. 使用伪尾递归减少程序栈空间占用，使得栈空间复杂度从 O(logn) ~ log(n) 变为：O(logn)。

3.1 改进：小规模数组使用直接插入排序

在小规模数组的情况下，直接插入排序的效率最好，当快速排序递归部分进入小数组范围，可以切换成直接插入排序。

// InsertSort 改进：当数组规模小时使用直接插入排序
func InsertSort(list []int) {
	n := len(list)
	// 进行 N-1 轮迭代
	for i := 1; i <= n-1; i++ {
		deal := list[i] // 待排序的数
		j := i - 1      // 待排序的数左边的第一个数的位置

		// 如果第一次比较，比左边的已排好序的第一个数小，那么进入处理
		if deal < list[j] {
			// 一直往左边找，比待排序大的数都往后挪，腾空位给待排序插入
			for ; j >= 0 && deal < list[j]; j-- {
				list[j+1] = list[j] // 某数后移，给待排序留空位
			}
			list[j+1] = deal // 结束了，待排序的数插入空位
		}
	}
}

func QuickSort1(array []int, begin, end int) {
	if begin < end {
		// 当数组小于 4 时使用直接插入排序
		if end-begin <= 4 {
			InsertSort(array[begin : end+1])
			return
		}

		// 进行切分
		loc := partition(array, begin, end)
		// 对左部分进行快排
		QuickSort1(array, begin, loc-1)
		// 对右部分进行快排
		QuickSort1(array, loc+1, end)
	}
}

直接插入排序在小规模数组下效率极好，我们只需将 end-begin <= 4 的递归部分换成直接插入排序，这部分表示小数组排序。

3.2 改进：三向切分

排序数列可能存在大量重复值，使用三向切分快速排序，将数组分成三部分，大于基准数，等于基准数，小于基准数，这个时候需要维护三个下标。

package main

import "fmt"

// QuickSort2 三切分的快速排序
func QuickSort2(array []int, begin, end int) {
	if begin < end {
		// 三向切分函数，返回左边和右边下标
		lt, gt := partition3(array, begin, end)
		// 从lt到gt的部分是三切分的中间数列
		// 左边三向快排
		QuickSort2(array, begin, lt-1)
		// 右边三向快排
		QuickSort2(array, gt+1, end)
	}
}

// 切分函数，并返回切分元素的下标
func partition3(array []int, begin, end int) (int, int) {
	lt := begin       // 左下标从第一位开始
	gt := end         // 右下标是数组的最后一位
	i := begin + 1    // 中间下标，从第二位开始
	v := array[begin] // 基准数

	// 以中间坐标为准
	for i <= gt {
		if array[i] > v { // 大于基准数，那么交换，右指针左移
			array[i], array[gt] = array[gt], array[i]
			gt--
		} else if array[i] < v { // 小于基准数，那么交换，左指针右移
			array[i], array[lt] = array[lt], array[i]
			lt++
			i++
		} else {
			i++
		}
	}

	return lt, gt
}

演示：

数列：4 8 2 4 4 4 7 9，基准数为 4

[4] [8] 2 4 4 4 7 [9]  从中间[]开始：8 > 4，中右[]进行交换，右边[]左移
[4] [9] 2 4 4 4 [7] 8  从中间[]开始：9 > 4，中右[]进行交换，右边[]左移
[4] [7] 2 4 4 [4] 9 8  从中间[]开始：7 > 4，中右[]进行交换，右边[]左移
[4] [4] 2 4 [4] 7 9 8  从中间[]开始：4 == 4，不需要交换，中间[]右移
[4] 4 [2] 4 [4] 7 9 8  从中间[]开始：2 < 4，中左[]需要交换，中间和左边[]右移
2 [4] 4 [4] [4] 7 9 8  从中间[]开始：4 == 4，不需要交换，中间[]右移
2 [4] 4 4 [[4]] 7 9 8  从中间[]开始：4 == 4，不需要交换，中间[]右移，因为已经重叠了
第一轮结果：2 4 4 4 4 7 9 8

分成三个数列：

2
4 4 4 4 (元素相同的会聚集在中间数列)
7 9 8

接着对第一个和最后一个数列进行递归即可。

示例图：

三切分，把小于基准数的扔到左边，大于基准数的扔到右边，相同的元素会进行聚集。

如果存在大量重复元素，排序速度将极大提高，将会是线性时间，因为相同的元素将会聚集在中间，这些元素不再进入下一个递归迭代。

三向切分主要来自荷兰国旗三色问题，该问题由 Dijkstra 提出。

 

假设有一条绳子，上面有红、白、蓝三种颜色的旗子，起初绳子上的旗子颜色并没有顺序，您希望将之分类，并排列为蓝、白、红的顺序，要如何移动次数才会最少，注意您只能在绳子上进行这个动作，而且一次只能调换两个旗子。

可以看到，上面的解答相当于使用三向切分一次，只要我们将白色旗子的值设置为 100，蓝色的旗子值设置为 0，红色旗子值设置为 200，以 100 作为基准数，第一次三向切分后三种颜色的旗就排好了，因为 蓝(0)白(100)红(200)。

注：艾兹格·W·迪科斯彻(Edsger Wybe Dijkstra，1930年5月11日~2002年8月6日)，荷兰人，计算机科学家，曾获图灵奖。

3.3 改进：伪尾递归优化

使用伪尾递归减少程序栈空间占用，使得栈空间复杂度从 O(logn) ~ log(n) 变为：O(logn)。

// 伪尾递归快速排序
func QuickSort3(array []int, begin, end int) {
	for begin < end {
		// 进行切分
		loc := partition(array, begin, end)

		// 那边元素少先排哪边
		if loc-begin < end-loc {
			// 先排左边
			QuickSort3(array, begin, loc-1)
			begin = loc + 1
		} else {
			// 先排右边
			QuickSort3(array, loc+1, end)
			end = loc - 1
		}
	}
}

很多人以为这样子是尾递归。其实这样的快排写法是伪装的尾递归，不是真正的尾递归，因为有 for 循环，不是直接 return QuickSort，递归还是不断地压栈，栈的层次仍然不断地增长。

但是，因为先让规模小的部分排序，栈的深度大大减少，程序栈最深不会超过 logn 层，这样堆栈最坏空间复杂度从 O(n) 降为 O(logn)。

这种优化也是一种很好的优化，因为栈的层数减少了，对于排序十亿个整数，也只要：log(100 0000 0000)=29.897，占用的堆栈层数最多 30 层，比不进行优化，可能出现的 O(n) 常数层好很多。

四、补充：非递归写法

非递归写法仅仅是将之前的递归栈转化为自己维持的手工栈。

// 非递归快速排序
func QuickSort5(array []int) {

	// 人工栈
	helpStack := new(LinkStack)

	// 第一次初始化栈，推入下标0，len(array)-1，表示第一次对全数组范围切分
	helpStack.Push(len(array) - 1)
	helpStack.Push(0)

	// 栈非空证明存在未排序的部分
	for !helpStack.IsEmpty() {
		// 出栈，对begin-end范围进行切分排序
		begin := helpStack.Pop() // 范围区间左边
		end := helpStack.Pop()   // 范围

		// 进行切分
		loc := partition(array, begin, end)

		// 右边范围入栈
		if loc+1 < end {
			helpStack.Push(end)
			helpStack.Push(loc + 1)
		}

		// 左边返回入栈
		if begin < loc-1 {
			helpStack.Push(loc - 1)
			helpStack.Push(begin)
		}
	}
}

本来需要进行递归的数组范围 begin,end，不使用递归，依次推入自己的人工栈，然后循环对人工栈进行处理。

我们可以看到没有递归，程序栈空间复杂度变为了：O(1)，但额外的存储空间产生了。

辅助人工栈结构 helpStack 占用了额外的空间，存储空间由原地排序的 O(1) 变成了 O(logn) ~ log(n)。

我们可以参考上面的伪尾递归版本，继续优化非递归版本，先让短一点的范围入栈，这样存储复杂度可以变为：O(logn)。如：

// 非递归快速排序优化
func QuickSort6(array []int) {

	// 人工栈
	helpStack := new(LinkStack)

	// 第一次初始化栈，推入下标0，len(array)-1，表示第一次对全数组范围切分
	helpStack.Push(len(array) - 1)
	helpStack.Push(0)

	// 栈非空证明存在未排序的部分
	for !helpStack.IsEmpty() {
		// 出栈，对begin-end范围进行切分排序
		begin := helpStack.Pop() // 范围区间左边
		end := helpStack.Pop()   // 范围

		// 进行切分
		loc := partition(array, begin, end)

		// 切分后右边范围大小
		rSize := -1
		// 切分后左边范围大小
		lSize := -1

		// 右边范围入栈
		if loc+1 < end {
			rSize = end - (loc + 1)
		}

		// 左边返回入栈
		if begin < loc-1 {
			lSize = loc - 1 - begin
		}

		// 两个范围，让范围小的先入栈，减少人工栈空间
		if rSize != -1 && lSize != -1 {
			if lSize > rSize {
				helpStack.Push(end)
				helpStack.Push(loc + 1)
				helpStack.Push(loc - 1)
				helpStack.Push(begin)
			} else {
				helpStack.Push(loc - 1)
				helpStack.Push(begin)
				helpStack.Push(end)
				helpStack.Push(loc + 1)
			}
		} else {
			if rSize != -1 {
				helpStack.Push(end)
				helpStack.Push(loc + 1)
			}

			if lSize != -1 {
				helpStack.Push(loc - 1)
				helpStack.Push(begin)
			}
		}
	}
}

五、补充：内置库使用快速排序的原因

首先堆排序，归并排序最好最坏时间复杂度都是：O(nlogn)，而快速排序最坏的时间复杂度是：O(n^2)，但是很多编程语言内置的排序算法使用的仍然是快速排序，这是为什么？

1. 这个问题有偏颇，选择排序算法要看具体的场景，Linux 内核用的排序算法就是堆排序，而 Java 对于数量比较多的复杂对象排序，内置排序使用的是归并排序，只是一般情况下，快速排序更快。
2. 归并排序有两个稳定，第一个稳定是排序前后相同的元素位置不变，第二个稳定是，每次都是很平均地进行排序，读取数据也是顺序读取，能够利用存储器缓存的特征，比如从磁盘读取数据进行排序。因为排序过程需要占用额外的辅助数组空间，所以这部分有代价损耗，但是原地手摇的归并排序克服了这个缺陷。
3. 复杂度中，大 O 有一个常数项被省略了，堆排序每次取最大的值之后，都需要进行节点翻转，重新恢复堆的特征，做了大量无用功，常数项比快速排序大，大部分情况下比快速排序慢很多。但是堆排序时间较稳定，不会出现快排最坏 O(n^2) 的情况，且省空间，不需要额外的存储空间和栈空间。
4. 当待排序数量大于16000个元素时，使用自底向上的堆排序比快速排序还快，可见此：https://core.ac.uk/download/pdf/82350265.pdf。
5. 快速排序最坏情况下复杂度高，主要在于切分不像归并排序一样平均，而是很依赖基准数的现在，我们通过改进，比如随机数，三切分等，这种最坏情况的概率极大的降低。大多数情况下，它并不会那么地坏，大多数快才是真的块。
6. 归并排序和快速排序都是分治法，排序的数据都是相邻的，而堆排序比较的数可能跨越很大的范围，导致局部性命中率降低，不能利用现代存储器缓存的特征，加载数据过程会损失性能。

对稳定性有要求的，要求排序前后相同元素位置不变，可以使用归并排序，Java 中的复杂对象类型，要求排序前后位置不能发生变化，所以小规模数据下使用了直接插入排序，大规模数据下使用了归并排序。

对栈，存储空间有要求的可以使用堆排序，比如 Linux 内核栈小，快速排序占用程序栈太大了，使用快速排序可能栈溢出，所以使用了堆排序。

六、补充：Golang 内置排序库 sort

在 Golang 中，标准库 sort 中使用了多种排序算法，值得研究。

例子：

package main

import (
	"fmt"
	"sort"
)

func InnerSort() {
	list := []struct {
		Name string
		Age  int
	}{
		{"A", 75},
		{"B", 4},
		{"C", 5},
		{"D", 5},
		{"E", 2},
		{"F", 5},
		{"G", 5},
	}

	sort.SliceStable(list, func(i, j int) bool { return list[i].Age < list[j].Age })
	fmt.Println(list)

	list2 := []struct {
		Name string
		Age  int
	}{
		{"A", 75},
		{"B", 4},
		{"C", 5},
		{"D", 5},
		{"E", 2},
		{"F", 5},
		{"G", 5},
	}

	sort.Slice(list2, func(i, j int) bool { return list2[i].Age < list2[j].Age })
	fmt.Println(list2)
}

func main() {
	InnerSort()
}

 其中 SliceStable 是稳定排序，使用了插入排序和归并排序：

 而 Slice 是一般的排序，不追求稳定排序，使用了快速排序:

快速排序限制程序栈的层数为： 2 * ceil( log(n+1) )，当递归超过该层时表示程序栈过深，内部会转为堆排序。

上述快速排序还使用了三种优化，第一种是递归时小数组转为插入排序，第二种是使用了中位数基准数，第三种使用了三向切分。

查找算法

在日常生活中，我们在寻找梦想。寻找，是我们的动力。

我们会在图书馆里面，找到人文相关的书架，然后按照索引去找书。拿到书时，我们很自然地通过目录去查找相应的章节。

在计算机的世界中，我们也想寻找。

计算机中，我们将数据存放在列表里，我们只解决了数据的存储问题，虽然我们可以遍历数据，将数据逐个取出来，但是我们还想要查找数据中的某个值。所以查找的需求出现了。

有几种查找算法：

1. 散列查找：也称哈希查找，有拉链法查找，也有线性探测法查找，拉链法使用数组链表结构，线性探测法使用数组。
2. 树查找：有搜索二叉树，平衡查找树如：红黑树，B树，AVL树，B+等，使用链表树结构。

我们接下来会具体分析每种查找算法。

哈希表：散列查找

一、线性查找

我们要通过一个 键key 来查找相应的 值value。有一种最简单的方式，就是将键值对存放在链表里，然后遍历链表来查找是否存在 key，存在则更新键对应的值，不存在则将键值对链接到链表上。

这种链表查找，最坏的时间复杂度为：O(n)，因为可能遍历到链表最后也没找到。

二、散列查找

有一种算法叫散列查找，也称哈希查找，是一种空间换时间的查找算法，依赖的数据结构称为哈希表或散列表：HashTable。

Hash: 翻译为散列，哈希，主要指压缩映射，它将一个比较大的域空间映射到一个比较小的域空间。 简单的说就是把任意长度的消息压缩到某一固定长度的消息摘要的函数。Hash 算法虽然是一种算法，但更像一种思想，没有一个固定的公式，只要符合这种思想的算法都称 Hash 算法。

散列查找，主要是将键进行 hash 计算得出一个大整数，然后与数组长度进行取余，这样一个比较大的域空间就只会映射到数组的下标范围，利用数组索引快的特征，用空间换时间的思路，使得查找的速度快于线性查找。

首先有一个大数组，每当存一个键值对时，先把键进行哈希，计算出的哈希值是一个整数，使用这个整数对数组长度取余，映射到数组的某个下标，把该键值对存起来，取数据时按同样的步骤进行查找。

有两种方式实现哈希表：线性探测法和拉链法。

三、哈希表：线性探测法

线性探测法实现的哈希表是一个大数组。

首先，哈希表数据结构会初始化 N 个大小的数组，然后存取键 key 时，会求键的哈希值 hash(key)，这是一个整数。然后与数组的大小进行取余：hash(key)%N，将会知道该键值对要存在数组的哪个位置。

如果数组该位置已经被之前的键值对占领了，也就是哈希冲突，那么会偏移加1，探测下个位置是否被占用，如果下个位置为空，那么占位，否则继续探测。查找时，也是查看该位置是否为该键，不是则继续往该位置的下一个位置查找。因为这个步骤是线性的，所以叫线性探测法。

四、哈希表：拉链法

拉链法实现的哈希表是一个数组链表，也就是数组中的元素是链表。数组链表很像一条条拉链，所以又叫拉链法查找。

首先，哈希表数据结构会初始化 N 个大小的数组，然后存取键 key 时，会求键的哈希值 hash(key)，这是一个整数。然后与数组的大小进行取余：hash(key)%N，将会知道该键值对要存在数组的哪个位置。

如果数组该位置已经被之前的键值对占领了，也就是哈希冲突，那么键值对会追加到之前键值对的后面，形成一条链表。

比如键 51 的哈希 hash(51) 假设为 4，那么 hash(51) % 4 = 4 % 4 = 0，所以放在数组的第一个位置，同样键 43 的哈希 hash(43) 假设为 8，那么 hash(43) % 4 = 8 % 4 = 0，同样要放在数组的第一个位置。

因为哈希冲突了，所以键 43 链接在键 51 后面。

五、哈希函数

当哈希冲突不严重的时候，查找某个键，只需要求哈希值，然后取余，定位到数组的某个下标即可，时间复杂度为：O(1)。

当哈希冲突十分严重的时候，每个数组元素对应的链表会越来越长，即使定位到数组的某个下标，也要遍历一条很长很长的链表，就退化为查找链表了，时间复杂度为：O(n)。

所以哈希表首先要解决的问题是寻找相对均匀，具有很好随机分布性的哈希函数 hash()，这样才不会扎堆冲突。

Golang 语言实现的哈希函数参考了以下两种哈希算法：

1. xxhash: https://code.google.com/p/xxhash
2. cityhash: https://code.google.com/p/cityhash

当然还有其他哈希算法如 MurmurHash: https://code.google.com/p/smhasher 。

还有哈希算法如 Md4 和 Md5 等。

因为研究均匀随机分布的哈希算法，是属于数学专家们的工作，我们在此不展开了。

我们使用号称计算速度最快的哈希 xxhash，我们直接用该库来实现哈希：GitHub - OneOfOne/xxhash: A native implementation of the excellent XXHash hashing algorithm.：

实现如下:

package main

import (
	"fmt"

	"github.com/OneOfOne/xxhash"
)

func XXHash(key []byte) uint64 {
	h := xxhash.New64()
	h.Write(key)
	return h.Sum64()
}

func main() {
	keys := []string{"hi", "my", "friend", "I", "love", "you", "my", "apple"}
	for _, key := range keys {
		fmt.Printf("xxhash('%s')=%d\n", key, XXHash([]byte(key)))
	}
}

输出：

PS D:\Workspace\Go\src\projects\demo> go run main.go
xxhash('hi')=16899831174130972922
xxhash('my')=13223332975333369668
xxhash('friend')=4642001949237932008
xxhash('I')=12677399051867059349    
xxhash('love')=12577149608739438547 
xxhash('you')=943396405629834470
xxhash('my')=13223332975333369668
xxhash('apple')=6379808199001010847

拿到哈希值之后，我们要对结果取余，方便定位到数组下标 index。如果数组的长度为 len，那么 index = xxhash(key) % len。

我们已经寻找到了计算较快，且均匀随机分布的哈希算法 xxhash 了，现在就是要解决取余操作中的数组长度选择的问题，数组的长度 len 应该如何选择？

比如数组长度 len=8，那么取余之后可能有这些结果:

1. xxhash(key) % 8 = 0，1，2，3，4，5，6，7

如果我们选择 2^x 作为数组长度有一个很好的优点，就是计算速度变快了，如下是一个恒等式：

1. 恒等式 hash % 2^k = hash & (2^k-1)，表示截断二进制的位数，保留后面的 k 位

这样取余 % 操作将变成按位 & 操作：

1. 哈希表数组长度 len=8，
2. 存在一个哈希值 hash=165，二进制表示为 1010 0101
4. 所以：
6. 165 % 8
7. = 165 % 2^3
8. = 165 & (2^3-1)
9. = 165 & 7
10. = 1010 0101 & 0000 0111
11. = 0000 0000 0101
12. = 5

选择 2^x 长度会使得计算速度更快，但是相当于截断二进制后保留后面的 k 位，如果存在很多哈希值的值很大，位数超过了 k 位，而二进制后 k 位都相同，那么会导致大片哈希冲突。

即使如此，存在很大哈希值的情况很少发生，大部分哈希值的二进制位数都不会超过 k 位，因此编程语言 Golang 使用了这种 2^x 长度作为哈希表的数组长度。

实际上 hash(key) % len 的分布是和 len 有关的，一组均匀分布的 hash(key) 在 len 是素数时才能做到均匀。

素数(prime number)，也叫质数，是指在大于 1 的自然数中，除了 1 和它本身以外不再有其他因数的自然数，也就是与任何数的最大公约数都为1。

举例如下：

1. f(n)为哈希表的下标，哈希表的长度是 m，而哈希值是 n，记 w=gcd(m,n) 为两个数的最大公约数，
3. 那么：
5. f(n) = n % m
6. = n - a*m (a=0,1,2,3,4...)
7. = w * (n/w-a*m/w)
9. 因为 w=gcd(m,n)，所以 (n/w-a*m/w) 是一个整数。
11. 所以哈希表的下标 f(n) 只会是 w=gcd(m,n) 的倍数，倍数就注定了不会均匀分布在 `[0,m-1]`，除非 w=1。
13. 在哈希值数列数量特别多的情况，对偶数和奇数数列进行取余求下标，如长度 m=5 和 m=6：
15. 哈希数值：2 4 6 8 10 12 14 16 18 20 22...
16. m=5时下标：2 4 1 3 0 2 4 1 3 0 2...
17. m=6时下标：2 4 0 2 4 0 2 4 0 2 4...
19. 哈希数值：1 3 5 7 9 11 13 15 17...
20. m=5时下标：1 3 0 2 4 1 3 0 2...
21. m=6时下标：1 3 5 1 3 5 1 3 5...
23. 偶数队列可以看到素数5一直重复 `2 4 1 3 0`，而合数6一直重复 `2 4 0`，只有素数均匀分布。
25. 奇数队列可以看到素数5一直重复 `1 3 0 2 4`，而合数6一直重复 `1 3 5`，只有素数均匀分布。
27. 将偶数和奇数数列合并起来，步长为1时，素数和奇数都一样均匀，仅当步长不为1时的随机数列，素数会更均匀点。

我们实现拉链哈希表的时候，为了数组扩容和计算更方便，仍然还是使用 2^x 的数组长度。

六、实现拉链哈希表

我们将实现一个简单的哈希表版本。

实现拉链哈希表有以下的一些操作：

1. 初始化：新建一个 2^x 个长度的数组，一开始 x 较小。
2. 添加键值：进行 hash(key) & (2^x-1)，定位到数组下标，查找数组下标对应的链表，如果链表有该键，更新其值，否则追加元素。
3. 获取键值：进行 hash(key) & (2^x-1)，定位到数组下标，查找数组下标对应的链表，如果链表不存在该键，返回 false，否则返回该值以及 true。
4. 删除键值：进行 hash(key) & (2^x-1)，定位到数组下标，查找数组下标对应的链表，如果链表不存在该键，直接返回，否则删除该键。
5. 进行键值增删时如果数组容量太大或者太小，需要相应缩容或扩容。

哈希查找的速度快，主要是利用空间换时间的优点。如果哈希表的数组特别大特别大，那么哈希冲突的几率就会降低。然而哈希表中的数组太大或太小都不行，太大浪费了空间，太小则哈希冲突太严重，所以需要对哈希表中的数组进行缩容和扩容。

如何伸缩主要根据哈希表的大小和已添加的元素数量来决定。假设哈希表的大小为 16，已添加到哈希表中的键值对数量是 8，我们称 8/16=0.5 为加载因子 factor。

我们可以设定加载因子 factor <= 0.125 时进行数组缩容，每次将容量砍半，当加载因子 factor >= 0.75 进行数组扩容，每次将容量翻倍。

大部分编程语言实现的哈希表只会扩容，不会缩容，因为对于一个经常访问的哈希表来说，缩容后会很快扩容，造成的哈希搬迁成本巨大，这个成本比起存储空间的浪费还大，所以我们在这里只实现哈希表扩容。

我们使用结构体 HashMap 来表示哈希表：

const (
    // 扩容因子
    expandFactor = 0.75
)
// 哈希表
type HashMap struct {
    array        []*keyPairs // 哈希表数组，每个元素是一个键值对
    capacity     int         // 数组容量
    len          int         // 已添加键值对元素数量
    capacityMask int         // 掩码，等于 capacity-1
    // 增删键值对时，需要考虑并发安全
    lock sync.Mutex
}
// 键值对，连成一个链表
type keyPairs struct {
    key   string      // 键
    value interface{} // 值
    next  *keyPairs   // 下一个键值对
}

其中 array 为哈希表数组，capacity 为哈希表的容量，capacityMask 为容量掩码，主要用来计算数组下标，len 为实际添加的键值对元素数量。

我们还使用了 lock 来实现并发安全，防止并发增删元素时数组伸缩，产生混乱。

使用 expandFactor = 0.75 作为扩容因子，没什么其他的理由，只是它刚刚好，你也可以设置成 0.72 等任何值。

6.1. 初始化哈希表

// 创建大小为 capacity 的哈希表
func NewHashMap(capacity int) *HashMap {
    // 默认大小为 16
    defaultCapacity := 1 << 4
    if capacity <= defaultCapacity {
        // 如果传入的大小小于默认大小，那么使用默认大小16
        capacity = defaultCapacity
    } else {
        // 否则，实际大小为大于 capacity 的第一个 2^k
        capacity = 1 << (int(math.Ceil(math.Log2(float64(capacity)))))
    }
    // 新建一个哈希表
    m := new(HashMap)
    m.array = make([]*keyPairs, capacity, capacity)
    m.capacity = capacity
    m.capacityMask = capacity - 1
    return m
}
// 返回哈希表已添加元素数量
func (m *HashMap) Len() int {
    return m.len
}

我们可以传入 capacity 来初始化当前哈希表数组容量，容量掩码 capacityMask = capacity-1 主要用来计算数组下标。

如果传入的容量小于默认容量 16，那么将 16 作为哈希表的初始数组大小。否则将第一个大于 capacity 的 2 ^ k 值作为数组的初始大小。

6.2. 计算哈希值和数组下标

// 求 key 的哈希值
var hashAlgorithm = func(key []byte) uint64 {
    h := xxhash.New64()
    h.Write(key)
    return h.Sum64()
}
// 对键进行哈希求值，并计算下标
func (m *HashMap) hashIndex(key string, mask int) int {
    // 求哈希
    hash := hashAlgorithm([]byte(key))
    // 求下标
    index := hash & uint64(mask)
    return int(index)
}

首先，为结构体生成一个 hashIndex 方法。

根据公式 hash(key) & (2^x-1)，使用 xxhash 哈希算法来计算键 key 的哈希值，并且和容量掩码 mask 进行 & 求得数组的下标，用来定位键值对该放在数组的哪个下标下。

6.2. 添加键值对

以下是添加键值对核心方法：

// 哈希表添加键值对
func (m *HashMap) Put(key string, value interface{}) {
    // 实现并发安全
    m.lock.Lock()
    defer m.lock.Unlock()
    // 键值对要放的哈希表数组下标
    index := m.hashIndex(key, m.capacityMask)
    // 哈希表数组下标的元素
    element := m.array[index]
    // 元素为空，表示空链表，没有哈希冲突，直接赋值
    if element == nil {
        m.array[index] = &keyPairs{
            key:   key,
            value: value,
        }
    } else {
        // 链表最后一个键值对
        var lastPairs *keyPairs
        // 遍历链表查看元素是否存在，存在则替换值，否则找到最后一个键值对
        for element != nil {
            // 键值对存在，那么更新值并返回
            if element.key == key {
                element.value = value
                return
            }
            lastPairs = element
            element = element.next
        }
        // 找不到键值对，将新键值对添加到链表尾端
        lastPairs.next = &keyPairs{
            key:   key,
            value: value,
        }
    }
    // 新的哈希表数量
    newLen := m.len + 1
    // 如果超出扩容因子，需要扩容
    if float64(newLen)/float64(m.capacity) >= expandFactor {
        // 新建一个原来两倍大小的哈希表
        newM := new(HashMap)
        newM.array = make([]*keyPairs, 2*m.capacity, 2*m.capacity)
        newM.capacity = 2 * m.capacity
        newM.capacityMask = 2*m.capacity - 1
        // 遍历老的哈希表，将键值对重新哈希到新哈希表
        for _, pairs := range m.array {
            for pairs != nil {
                // 直接递归Put
                newM.Put(pairs.key, pairs.value)
                pairs = pairs.next
            }
        }
        // 替换老的哈希表
        m.array = newM.array
        m.capacity = newM.capacity
        m.capacityMask = newM.capacityMask
    }
    m.len = newLen
}

首先使用锁实现了并发安全：

1. m.lock.Lock()
2. defer m.lock.Unlock()

接着使用哈希算法计算出数组的下标，并取出该下标的元素：

1. // 键值对要放的哈希表数组下标
2. index := m.hashIndex(key, m.capacityMask)
4. // 哈希表数组下标的元素
5. element := m.array[index]

如果该元素为空表示链表是空的，不存在哈希冲突，直接将键值对作为链表的第一个元素：

1. // 元素为空，表示空链表，没有哈希冲突，直接赋值
2. if element == nil {
3. m.array[index] = &keyPairs{
4. key: key,
5. value: value,
6. }
7. }

否则，则遍历链表，查找键是否存在：

1. // 链表最后一个键值对
2. var lastPairs *keyPairs
4. // 遍历链表查看元素是否存在，存在则替换值，否则找到最后一个键值对
5. for element != nil {
6. // 键值对存在，那么更新值并返回
7. if element.key == key {
8. element.value = value
9. return
10. }
12. lastPairs = element
13. element = element.next
14. }

当 element.key == key ，那么键存在，直接更新值，退出该函数。否则，继续往下遍历。

当跳出 for element != nil 时，表示找不到键值对，那么往链表尾部添加该键值对：

1. // 找不到键值对，将新键值对添加到链表尾端
2. lastPairs.next = &keyPairs{
3. key: key,
4. value: value,
5. }

最后，检查是否需要扩容，如果需要则扩容：

         // 新的哈希表数量
         newLen := m.len + 1
         // 如果超出扩容因子，需要扩容
         if float64(newLen)/float64(m.capacity) >= expandFactor {
             // 新建一个原来两倍大小的哈希表
             newM := new(HashMap)
             newM.array = make([]*keyPairs, 2*m.capacity, 2*m.capacity)
             newM.capacity = 2 * m.capacity
             newM.capacityMask = 2*m.capacity - 1
             // 遍历老的哈希表，将键值对重新哈希到新哈希表
             for _, pairs := range m.array {
                 for pairs != nil {
                     // 直接递归Put
                     newM.Put(pairs.key, pairs.value)
                     pairs = pairs.next
                 }
             }
             // 替换老的哈希表
             m.array = newM.array
             m.capacity = newM.capacity
             m.capacityMask = newM.capacityMask
         }
         m.len = newLen

创建了一个新的两倍大小的哈希表：newM := new(HashMap)，然后遍历老哈希表中的键值对，重新 Put 进新哈希表。

最后将新哈希表的属性赋予老哈希表。

6.3. 获取键值对

1. // 哈希表获取键值对
2. func (m *HashMap) Get(key string) (value interface{}, ok bool) {
3. // 实现并发安全
4. m.lock.Lock()
5. defer m.lock.Unlock()
7. // 键值对要放的哈希表数组下标
8. index := m.hashIndex(key, m.capacityMask)
10. // 哈希表数组下标的元素
11. element := m.array[index]
13. // 遍历链表查看元素是否存在，存在则返回
14. for element != nil {
15. if element.key == key {
16. return element.value, true
17. }
19. element = element.next
20. }
22. return
23. }

同样先加锁实现并发安全，然后进行哈希算法计算出数组下标：index := m.hashIndex(key, m.capacityMask)，取出元素：element := m.array[index]。

对链表进行遍历：

1. // 遍历链表查看元素是否存在，存在则返回
2. for element != nil {
3. if element.key == key {
4. return element.value, true
5. }
7. element = element.next
8. }

如果键在哈希表中存在，返回键的值 element.value 和 true。

6.4. 删除键值对

// 哈希表删除键值对
func (m *HashMap) Delete(key string) {
    // 实现并发安全
    m.lock.Lock()
    defer m.lock.Unlock()
    // 键值对要放的哈希表数组下标
    index := m.hashIndex(key, m.capacityMask)
    // 哈希表数组下标的元素
    element := m.array[index]
    // 空链表，不用删除，直接返回
    if element == nil {
        return
    }
    // 链表的第一个元素就是要删除的元素
    if element.key == key {
        // 将第一个元素后面的键值对链上
        m.array[index] = element.next
        m.len = m.len - 1
        return
    }
    // 下一个键值对
    nextElement := element.next
    for nextElement != nil {
        if nextElement.key == key {
            // 键值对匹配到，将该键值对从链中去掉
            element.next = nextElement.next
            m.len = m.len - 1
            return
        }
        element = nextElement
        nextElement = nextElement.next
    }
}

删除键值对，如果键值对存在，那么删除，否则什么都不做。

键值对删除时，哈希表并不会缩容，我们不实现缩容。

同样先加锁实现并发安全，然后进行哈希算法计算出数组下标：index := m.hashIndex(key, m.capacityMask)，取出元素：element := m.array[index]。

如果元素是空的，表示链表为空，那么直接返回：

1. // 空链表，不用删除，直接返回
2. if element == nil {
3. return
4. }

否则查看链表第一个元素的键是否匹配：element.key == key，如果匹配，那么对链表头部进行替换，链表的第二个元素补位成为链表头部：

1. // 链表的第一个元素就是要删除的元素
2. if element.key == key {
3. // 将第一个元素后面的键值对链上
4. m.array[index] = element.next
5. m.len = m.len - 1
6. return
7. }

如果链表的第一个元素不匹配，那么从第二个元素开始遍历链表，找到时将该键值对删除，然后将前后两个键值对连接起来：

1. // 下一个键值对
2. nextElement := element.next
3. for nextElement != nil {
4. if nextElement.key == key {
5. // 键值对匹配到，将该键值对从链中去掉
6. element.next = nextElement.next
7. m.len = m.len - 1
8. return
9. }
11. element = nextElement
12. nextElement = nextElement.next
13. }

6.4. 遍历打印哈希表

1. // 哈希表遍历
2. func (m *HashMap) Range() {
3. // 实现并发安全
4. m.lock.Lock()
5. defer m.lock.Unlock()
6. for _, pairs := range m.array {
7. for pairs != nil {
8. fmt.Printf("'%v'='%v',", pairs.key, pairs.value)
9. pairs = pairs.next
10. }
11. }
13. fmt.Println()
14. }

遍历哈希表比较简单，粗暴的遍历数组，如果数组中的链表不为空，打印链表中的元素。

6.4. 示例运行

func main() {
    // 新建一个哈希表
    hashMap := NewHashMap(16)
    // 放35个值
    for i := 0; i < 35; i++ {
        hashMap.Put(fmt.Sprintf("%d", i), fmt.Sprintf("v%d", i))
    }
    fmt.Println("cap:", hashMap.Capacity(), "len:", hashMap.Len())
    // 打印全部键值对
    hashMap.Range()
    key := "4"
    value, ok := hashMap.Get(key)
    if ok {
        fmt.Printf("get '%v'='%v'\n", key, value)
    } else {
        fmt.Printf("get %v not found\n", key)
    }
    // 删除键
    hashMap.Delete(key)
    fmt.Println("after delete cap:", hashMap.Capacity(), "len:", hashMap.Len())
    value, ok = hashMap.Get(key)
    if ok {
        fmt.Printf("get '%v'='%v'\n", key, value)
    } else {
        fmt.Printf("get %v not found\n", key)
    }
}

输出：

cap: 64 len: 35
'20'='v20','16'='v16','4'='v4','32'='v32','2'='v2','28'='v28','24'='v24','10'='v10','9'='v9','15'='v15','12'='v12','29'='v29','3'='v3','19'='v19','30'='v30','27'='v27','14'='v14','13'='v13','22'='v22','7'='v7','11'='v11','23'='v23','1'='v1','31'='v31','18'='v18','17'='v17','8'='v8','26'='v26','25'='v25','0'='v0','5'='v5','34'='v34','21'='v21','6'='v6','33'='v33',
get '4'='v4'
after delete cap: 64 len: 34
get 4 not found

首先 hashMap := NewHashMap(16) 新建一个 16 容量的哈希表。然后往哈希表填充 35 个键值对，遍历打印出来 hashMap.Range() 。

可以看到容量从 16 一直翻倍到 `64，而打印出来的键值对是随机的。

获取键值对时：value, ok := hashMap.Get(key) 能正常获取到值：get '4'='v4'。

删除键值对：hashMap.Delete(key) 后，哈希表的容量不变，但元素数量变少：after delete cap: 128 len: 34。

尝试再一次获取键 4，报错：get 4 not found。

七. 总结

哈希表查找，是一种用空间换时间的查找算法，时间复杂度能达到：O(1)，最坏情况下退化到查找链表：O(n)。但均匀性很好的哈希算法以及合适空间大小的数组，在很大概率避免了最坏情况。

哈希表在添加元素时会进行伸缩，会造成较大的性能消耗，所以有时候会用到其他的查找算法：树查找算法。

树查找算法在后面的章节会进行介绍。

二叉查找树

二叉查找树，又叫二叉排序树，二叉搜索树，是一种有特定规则的二叉树，定义如下：

1. 它是一棵二叉树，或者是空树。
2. 左子树所有节点的值都小于它的根节点，右子树所有节点的值都大于它的根节点。
3. 左右子树也是一棵二叉查找树。

二叉查找树的特点是，一直往左儿子往下找左儿子，可以找到最小的元素，一直往右儿子找右儿子，可以找到最大的元素。

看起来，我们可以用它来实现元素排序，可是我们却使用了二叉堆来实现了堆排序，因为二叉查找树不保证是一个平衡的二叉树，最坏情况下二叉查找树会退化成一个链表，也就是所有节点都没有左子树或者没有右子树，树的层次太深导致排序性能太差。

使用二分查找，可以很快在一棵二叉查找树中找到我们需要的值。

我们来分析二叉查找树添加，删除，查找元素的方法。

一、添加元素

以下是一个二叉查找树的表示：

// 二叉查找树
type BinarySearchTree struct {
    Root *BinarySearchTreeNode // 树根节点
}
// 二叉查找树节点
type BinarySearchTreeNode struct {
    Value int64                 // 值
    Times int64                 // 值出现的次数
    Left  *BinarySearchTreeNode // 左子树
    Right *BinarySearchTreeNode // 右字树
}
// 初始化一个二叉查找树
func NewBinarySearchTree() *BinarySearchTree {
    return new(BinarySearchTree)
}

一个节点代表一个元素，节点的 Value 值是用来进行二叉查找的关键，当 Value 值重复时，我们将值出现的次数 Times 加 1。添加元素代码如下：

// 添加元素
func (tree *BinarySearchTree) Add(value int64) {
    // 如果没有树根，证明是棵空树，添加树根后返回
    if tree.Root == nil {
        tree.Root = &BinarySearchTreeNode{Value: value}
        return
    }
    // 将值添加进去
    tree.Root.Add(value)
}
func (node *BinarySearchTreeNode) Add(value int64) {
    if value < node.Value {
        // 如果插入的值比节点的值小，那么要插入到该节点的左子树中
        // 如果左子树为空，直接添加
        if node.Left == nil {
            node.Left = &BinarySearchTreeNode{Value: value}
        } else {
            // 否则递归
            node.Left.Add(value)
        }
    } else if value > node.Value {
        // 如果插入的值比节点的值大，那么要插入到该节点的右子树中
        // 如果右子树为空，直接添加
        if node.Right == nil {
            node.Right = &BinarySearchTreeNode{Value: value}
        } else {
            // 否则递归
            node.Right.Add(value)
        }
    } else {
        // 值相同，不需要添加，值出现的次数加1即可
        node.Times = node.Times + 1
    }
}

如果添加元素时是棵空树，那么初始化根节点。

然后添加的值和根节点比较，判断是要插入到根节点左子树还是右子树，还是不用插入。

当值比根节点小时，元素要插入到根节点的左子树中，当值比根节点大时，元素要插入到根节点的右子树中，相等时不插入，只更新次数。

然后再分别对根节点的左子树和右子树进行递归操作即可。

二、查找最大值或最小值的元素

查找最大值和最小值比较简单，一直往左儿子往下找左儿子，可以找到最小的元素，一直往右儿子找右儿子，可以找到最大的元素。

// 找出最小值的节点
func (tree *BinarySearchTree) FindMinValue() *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMinValue()
}
func (node *BinarySearchTreeNode) FindMinValue() *BinarySearchTreeNode {
    // 左子树为空，表面已经是最左的节点了，该值就是最小值
    if node.Left == nil {
        return node
    }
    // 一直左子树递归
    return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *BinarySearchTree) FindMaxValue() *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMaxValue()
}
func (node *BinarySearchTreeNode) FindMaxValue() *BinarySearchTreeNode {
    // 右子树为空，表面已经是最右的节点了，该值就是最大值
    if node.Right == nil {
        return node
    }
    // 一直右子树递归
    return node.Right.FindMaxValue()
}

三、查找指定元素

二分查找的技巧也在这里有用武之地了：

// 查找节点
func (tree *BinarySearchTree) Find(value int64) *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.Find(value)
}
func (node *BinarySearchTreeNode) Find(value int64) *BinarySearchTreeNode {
    if value == node.Value {
        // 如果该节点刚刚等于该值，那么返回该节点
        return node
    } else if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        if node.Left == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Left.Find(value)
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        if node.Right == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Right.Find(value)
    }
}

如果是空树，返回 nil，否则与根节点比较。

如果刚刚好等于根节点的值，返回该节点，否则根据值的比较，继续往左子树或右字树递归查找。

四、查找指定元素的父亲

与查找指定元素一样，只不过追踪的是该元素的父亲节点。

// 查找指定节点的父亲
func (tree *BinarySearchTree) FindParent(value int64) *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    // 如果根节点等于该值，根节点其没有父节点，返回nil
    if tree.Root.Value == value {
        return nil
    }
    return tree.Root.FindParent(value)
}
func (node *BinarySearchTreeNode) FindParent(value int64) *BinarySearchTreeNode {
    // 外层没有值相等的判定，因为在内层已经判定完毕后返回父亲节点。
    if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        leftTree := node.Left
        if leftTree == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        // 左子树的根节点的值刚好等于该值，那么父亲就是现在的node，返回
        if leftTree.Value == value {
            return node
        } else {
            return leftTree.FindParent(value)
        }
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        rightTree := node.Right
        if rightTree == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        // 右子树的根节点的值刚好等于该值，那么父亲就是现在的node，返回
        if rightTree.Value == value {
            return node
        } else {
            return rightTree.FindParent(value)
        }
    }
}

代码相应的进行了调整，方便获取到父亲节点。

如果返回的父亲节点为空，表示没有父亲。

五、删除元素

删除元素有四种情况：

1. 第一种情况，删除的是根节点，且根节点没有儿子，直接删除即可。
2. 第二种情况，删除的节点有父亲节点，但没有子树，也就是删除的是叶子节点，直接删除即可。
3. 第三种情况，删除的节点下有两个子树，因为右子树的值都比左子树大，那么用右子树中的最小元素来替换删除的节点，这时二叉查找树的性质又满足了。右子树的最小元素，只要一直往右子树的左边一直找一直找就可以找到。
4. 第四种情况，删除的节点只有一个子树，那么该子树直接替换被删除的节点即可。

代码实现如下：

// 删除指定的元素
func (tree *BinarySearchTree) Delete(value int64) {
    if tree.Root == nil {
        // 如果是空树，直接返回
        return
    }
    // 查找该值是否存在
    node := tree.Root.Find(value)
    if node == nil {
        // 不存在该值，直接返回
        return
    }
    // 查找该值的父亲节点
    parent := tree.Root.FindParent(value)
    // 第一种情况，删除的是根节点，且根节点没有儿子
    if parent == nil && node.Left == nil && node.Right == nil {
        // 置空后直接返回
        tree.Root = nil
        return
    } else if node.Left == nil && node.Right == nil {
        // 第二种情况，删除的节点有父亲节点，但没有子树
        // 如果删除的是节点是父亲的左儿子，直接将该值删除即可
        if parent.Left != nil && value == parent.Left.Value {
            parent.Left = nil
        } else {
            // 删除的原来是父亲的右儿子，直接将该值删除即可
            parent.Right = nil
        }
        return
    } else if node.Left != nil && node.Right != nil {
        // 第三种情况，删除的节点下有两个子树，因为右子树的值都比左子树大，那么用右子树中的最小元素来替换删除的节点。
        // 右子树的最小元素，只要一直往右子树的左边一直找一直找就可以找到，替换后二叉查找树的性质又满足了。
        // 找右子树中最小的值，一直往右子树的左边找
        minNode := node.Right
        for minNode.Left != nil {
            minNode = minNode.Left
        }
        // 把最小的节点删掉
        tree.Delete(minNode.Value)
        // 最小值的节点替换被删除节点
        node.Value = minNode.Value
        node.Times = minNode.Times
    } else {
        // 第四种情况，只有一个子树，那么该子树直接替换被删除的节点即可
        // 父亲为空，表示删除的是根节点，替换树根
        if parent == nil {
            if node.Left != nil {
                tree.Root = node.Left
            } else {
                tree.Root = node.Right
            }
            return
        }
        // 左子树不为空
        if node.Left != nil {
            // 如果删除的是节点是父亲的左儿子，让删除的节点的左子树接班
            if parent.Left != nil && value == parent.Left.Value {
                parent.Left = node.Left
            } else {
                parent.Right = node.Left
            }
        } else {
            // 如果删除的是节点是父亲的左儿子，让删除的节点的右子树接班
            if parent.Left != nil && value == parent.Left.Value {
                parent.Left = node.Right
            } else {
                parent.Right = node.Right
            }
        }
    }
}

首先查找到要删除元素的节点：tree.Root.Find(value)，然后找到该节点父亲：tree.Root.FindParent(value)，根据四种不同情况对删除节点进行补位。核心在于，第三种情况下，删除的节点有两个子树情况下，需要用右子树中最小的节点来替换被删除节点。

上面的代码可以优化，可以在查找删除元素的节点时顺道查出其父亲节点，不必要分开查询父亲节点，在第三种情况下查出右子树的最小节点时可以直接将其移除，不必递归使用 tree.Delete(minNode.Value)。

由于这种通用形式的二叉查找树实现甚少使用，大部分程序都使用了AVL树或红黑树，以上优化理解即可。

六、中序遍历(实现排序)

使用二叉查找树可以实现排序，只需要对树进行中序遍历即可。

我们先打印出左子树，然后打印根节点的值，再打印右子树，这是一个递归的过程。

// 中序遍历
func (tree *BinarySearchTree) MidOrder() {
    tree.Root.MidOrder()
}
func (node *BinarySearchTreeNode) MidOrder() {
    if node == nil {
        return
    }
    // 先打印左子树
    node.Left.MidOrder()
    // 按照次数打印根节点
    for i := 0; i <= int(node.Times); i++ {
        fmt.Println(node.Value)
    }
    // 打印右子树
    node.Right.MidOrder()
}

七、完整代码

package main
import (
    "fmt"
)
// 二叉查找树节点
type BinarySearchTree struct {
    Root *BinarySearchTreeNode // 树根节点
}
// 二叉查找树节点
type BinarySearchTreeNode struct {
    Value int64                 // 值
    Times int64                 // 值出现的次数
    Left  *BinarySearchTreeNode // 左子树
    Right *BinarySearchTreeNode // 右字树
}
// 初始化一个二叉查找树
func NewBinarySearchTree() *BinarySearchTree {
    return new(BinarySearchTree)
}
// 添加元素
func (tree *BinarySearchTree) Add(value int64) {
    // 如果没有树根，证明是棵空树，添加树根后返回
    if tree.Root == nil {
        tree.Root = &BinarySearchTreeNode{Value: value}
        return
    }
    // 将值添加进去
    tree.Root.Add(value)
}
func (node *BinarySearchTreeNode) Add(value int64) {
    if value < node.Value {
        // 如果插入的值比节点的值小，那么要插入到该节点的左子树中
        // 如果左子树为空，直接添加
        if node.Left == nil {
            node.Left = &BinarySearchTreeNode{Value: value}
        } else {
            // 否则递归
            node.Left.Add(value)
        }
    } else if value > node.Value {
        // 如果插入的值比节点的值大，那么要插入到该节点的右子树中
        // 如果右子树为空，直接添加
        if node.Right == nil {
            node.Right = &BinarySearchTreeNode{Value: value}
        } else {
            // 否则递归
            node.Right.Add(value)
        }
    } else {
        // 值相同，不需要添加，值出现的次数加1即可
        node.Times = node.Times + 1
    }
}
// 找出最小值的节点
func (tree *BinarySearchTree) FindMinValue() *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMinValue()
}
func (node *BinarySearchTreeNode) FindMinValue() *BinarySearchTreeNode {
    // 左子树为空，表面已经是最左的节点了，该值就是最小值
    if node.Left == nil {
        return node
    }
    // 一直左子树递归
    return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *BinarySearchTree) FindMaxValue() *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMaxValue()
}
func (node *BinarySearchTreeNode) FindMaxValue() *BinarySearchTreeNode {
    // 右子树为空，表面已经是最右的节点了，该值就是最大值
    if node.Right == nil {
        return node
    }
    // 一直右子树递归
    return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *BinarySearchTree) Find(value int64) *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.Find(value)
}
func (node *BinarySearchTreeNode) Find(value int64) *BinarySearchTreeNode {
    if value == node.Value {
        // 如果该节点刚刚等于该值，那么返回该节点
        return node
    } else if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        if node.Left == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Left.Find(value)
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        if node.Right == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Right.Find(value)
    }
}
// 查找指定节点的父亲
func (tree *BinarySearchTree) FindParent(value int64) *BinarySearchTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    // 如果根节点等于该值，根节点其没有父节点，返回nil
    if tree.Root.Value == value {
        return nil
    }
    return tree.Root.FindParent(value)
}
func (node *BinarySearchTreeNode) FindParent(value int64) *BinarySearchTreeNode {
    // 外层没有值相等的判定，因为在内层已经判定完毕后返回父亲节点。
    if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        leftTree := node.Left
        if leftTree == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        // 左子树的根节点的值刚好等于该值，那么父亲就是现在的node，返回
        if leftTree.Value == value {
            return node
        } else {
            return leftTree.FindParent(value)
        }
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        rightTree := node.Right
        if rightTree == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        // 右子树的根节点的值刚好等于该值，那么父亲就是现在的node，返回
        if rightTree.Value == value {
            return node
        } else {
            return rightTree.FindParent(value)
        }
    }
}
// 删除指定的元素
func (tree *BinarySearchTree) Delete(value int64) {
    if tree.Root == nil {
        // 如果是空树，直接返回
        return
    }
    // 查找该值是否存在
    node := tree.Root.Find(value)
    if node == nil {
        // 不存在该值，直接返回
        return
    }
    // 查找该值的父亲节点
    parent := tree.Root.FindParent(value)
    // 第一种情况，删除的是根节点，且根节点没有儿子
    if parent == nil && node.Left == nil && node.Right == nil {
        // 置空后直接返回
        tree.Root = nil
        return
    } else if node.Left == nil && node.Right == nil {
        //  第二种情况，删除的节点有父亲节点，但没有子树
        // 如果删除的是节点是父亲的左儿子，直接将该值删除即可
        if parent.Left != nil && value == parent.Left.Value {
            parent.Left = nil
        } else {
            // 删除的原来是父亲的右儿子，直接将该值删除即可
            parent.Right = nil
        }
        return
    } else if node.Left != nil && node.Right != nil {
        // 第三种情况，删除的节点下有两个子树，因为右子树的值都比左子树大，那么用右子树中的最小元素来替换删除的节点，这时二叉查找树的性质又满足了。
        // 找右子树中最小的值，一直往右子树的左边找
        minNode := node.Right
        for minNode.Left != nil {
            minNode = minNode.Left
        }
        // 把最小的节点删掉
        tree.Delete(minNode.Value)
        // 最小值的节点替换被删除节点
        node.Value = minNode.Value
        node.Times = minNode.Times
    } else {
        // 第四种情况，只有一个子树，那么该子树直接替换被删除的节点即可
        // 父亲为空，表示删除的是根节点，替换树根
        if parent == nil {
            if node.Left != nil {
                tree.Root = node.Left
            } else {
                tree.Root = node.Right
            }
            return
        }
        // 左子树不为空
        if node.Left != nil {
            // 如果删除的是节点是父亲的左儿子，让删除的节点的左子树接班
            if parent.Left != nil && value == parent.Left.Value {
                parent.Left = node.Left
            } else {
                parent.Right = node.Left
            }
        } else {
            // 如果删除的是节点是父亲的左儿子，让删除的节点的右子树接班
            if parent.Left != nil && value == parent.Left.Value {
                parent.Left = node.Right
            } else {
                parent.Right = node.Right
            }
        }
    }
}
// 中序遍历
func (tree *BinarySearchTree) MidOrder() {
    tree.Root.MidOrder()
}
func (node *BinarySearchTreeNode) MidOrder() {
    if node == nil {
        return
    }
    // 先打印左子树
    node.Left.MidOrder()
    // 按照次数打印根节点
    for i := 0; i <= int(node.Times); i++ {
        fmt.Println(node.Value)
    }
    // 打印右子树
    node.Right.MidOrder()
}
func main() {
    values := []int64{3, 6, 8, 20, 9, 2, 6, 8, 9, 3, 5, 40, 7, 9, 13, 6, 8}
    // 初始化二叉查找树并添加元素
    tree := NewBinarySearchTree()
    for _, v := range values {
        tree.Add(v)
    }
    // 找到最大值或最小值的节点
    fmt.Println("find min value:", tree.FindMinValue())
    fmt.Println("find max value:", tree.FindMaxValue())
    // 查找不存在的99
    node := tree.Find(99)
    if node != nil {
        fmt.Println("find it 99!")
    } else {
        fmt.Println("not find it 99!")
    }
    // 查找存在的9
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    // 删除存在的9后，再查找9
    tree.Delete(9)
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    // 中序遍历，实现排序
    tree.MidOrder()
}

八、总结

二叉查找树可能退化为链表，也可能是一棵非常平衡的二叉树，查找，添加，删除元素的时间复杂度取决于树的高度 h。

1. 当二叉树是满的时，树的高度是最小的，此时树节点数量 n 和高度 h 的关系为：h = log(n)。
2. 当二叉树是一个链表时，此时树节点数量 n 和高度 h 的关系为：h = n。

二叉查找树的效率来源其二分查找的特征，时间复杂度在于二叉树的高度，因此查找，添加和删除的时间复杂度范围为 log(n)~n。

为了提高二叉查找树查找的速度，树的高度要尽可能的小。AVL树和红黑树都是相对平衡的二叉查找树，因为特殊的旋转平衡操作，树的高度被大大压低。它们查找效率较高，添加，删除，查找操作的平均时间复杂度都为 log(n)，经常在各种程序中被使用。

二叉查找树是后面要学习的高级数据结构AVL树，红黑树的基础。

AVL树

二叉查找树的树高度影响了查找的效率，需要尽量减小树的高度，AVL树正是这样的树。

一、AVL树介绍

AVL树是一棵严格自平衡的二叉查找树，1962年，发明者 Adelson-Velsky 和 Landis 发表了论文，以两个作者的名字命名了该数据结构，这是较早发明的平衡二叉树。

定义如下：

1. 首先它是一棵二叉查找树。
2. 任意一个节点的左右子树最大高度差为1。

由于树特征定义，我们可以计算出其高度 h 的上界 h<=1.44log(n)，也就是最坏情况下，树的高度约等于 1.44log(n)。

假设高度 h 的AVL树最少有 f(h) 个节点，因为左右子树的高度差不能大于1，所以左子树和右子树最少节点为： f(h-1)，f(h-2)。

因此，树根节点加上左右子树的节点，满足公式 f(h) = 1 + f(h-1) + f(h-2)，初始条件 f(0)=0,f(1)=1。

经过数学的推算可以得出 h<=1.44log(n)，由于计算过程超纲了，在此不进行演算。

树的高度被限制于 1.44log(n)， 所以查找元素时使用二分查找，最坏查找 1.44log(n) 次，此时最坏时间复杂度为 1.44log(n)，去掉常数项，时间复杂度为：log(n)。

为了维持AVL树的特征，每次添加和删除元素都需要一次或多次旋转来调整树的平衡。调整的依据来自于二叉树节点的平衡因子：节点的左子树与右子树的高度差称为该节点的平衡因子，约束范围为 [-1，0，1]。

平衡二叉查找树比较难以理解的是添加和删除元素时的调整操作，我们将会具体分析。

二、AVL树基本结构

AVL树的数据结构如下：

// AVL树
type AVLTree struct {
    Root *AVLTreeNode // 树根节点
}
// AVL节点
type AVLTreeNode struct {
    Value  int64                 // 值
    Times  int64                 // 值出现的次数
    Height int64                 // 该节点作为树根节点，树的高度，方便计算平衡因子
    Left   *AVLTreeNode // 左子树
    Right  *AVLTreeNode // 右字树
}
// 初始化一个AVL树
func NewAVLTree() *AVLTree {
    return new(AVLTree)
}

其中 Height 表示以该节点作为树的根节点时该树的高度，方便计算平衡因子。

更新树的高度，代码如下：

// 更新节点的树高度
func (node *AVLTreeNode) UpdateHeight() {
    if node == nil {
        return
    }
    var leftHeight, rightHeight int64 = 0, 0
    if node.Left != nil {
        leftHeight = node.Left.Height
    }
    if node.Right != nil {
        rightHeight = node.Right.Height
    }
    // 哪个子树高算哪棵的
    maxHeight := leftHeight
    if rightHeight > maxHeight {
        maxHeight = rightHeight
    }
    // 高度加上自己那一层
    node.Height = maxHeight + 1
}

计算树的平衡因子，也就是左右子树的高度差，代码如下：

// 计算平衡因子
func (node *AVLTreeNode) BalanceFactor() int64 {
    var leftHeight, rightHeight int64 = 0, 0
    if node.Left != nil {
        leftHeight = node.Left.Height
    }
    if node.Right != nil {
        rightHeight = node.Right.Height
    }
    return leftHeight - rightHeight
}

三、AVL树添加元素

添加元素前需要定位到元素的位置，也就是使用二分查找找到该元素需要插入的地方。

插入后，需要满足所有节点的平衡因子在 [-1，0，1] 范围内，如果不在，需要进行旋转调整。

旋转有四种情况：

1. 在右子树上插上右儿子导致失衡，左旋，转一次。
2. 在左子树上插上左儿子导致失衡，右旋，转一次。
3. 在左子树上插上右儿子导致失衡，先左后右旋，转两次。
4. 在右子树上插上左儿子导致失衡，先右后左旋，转两次。

旋转规律记忆法：单旋和双旋，单旋反方向，双旋同方向。

以下示意图摘自维基百科，阅读代码时可以参考。

3.1. 左子树插左儿子：单右旋

在左子树上插上左儿子导致失衡，需要单右旋：

因为红色元素 2 的产生，其最近的父亲节点 Root 失衡了，元素 2 导致了元素 Root=5 的失衡，需要调整。

将 Pivot=3 代替元素 5 的位置成为新的 Root，然后元素 5 委屈一下成为 3 的右儿子，而 3 的右儿子变成了 5 的左儿子，如上图。

相应调整后树的高度降低了，该失衡消失。我们可以看到红色元素 2 有两个儿子，实际上在添加操作时它是一个新的节点，是没有儿子的，这种有儿子的情况只发生在删除操作。

如果一时难以理解，可以多看几次图好好思考。

代码如下：

// 单右旋操作，看图说话
func RightRotation(Root *AVLTreeNode) *AVLTreeNode {
    // 只有Pivot和B，Root位置变了
    Pivot := Root.Left
    B := Pivot.Right
    Pivot.Right = Root
    Root.Left = B
    // 只有Root和Pivot变化了高度
    Root.UpdateHeight()
    Pivot.UpdateHeight()
    return Pivot
}

3.2. 右子树插右儿子：单左旋

在右子树上插上右儿子导致失衡，需要单左旋：

 代码如下：

// 单左旋操作，看图说话
func LeftRotation(Root *AVLTreeNode) *AVLTreeNode {
    // 只有Pivot和B，Root位置变了
    Pivot := Root.Right
    B := Pivot.Left
    Pivot.Left = Root
    Root.Right = B
    // 只有Root和Pivot变化了高度
    Root.UpdateHeight()
    Pivot.UpdateHeight()
    return Pivot
}

3.3. 左子树插右儿子：先左后右旋

在左子树上插上右儿子导致失衡，先左后右旋：

代码如下：

// 先左后右旋操作，看图说话
func LeftRightRotation(node *AVLTreeNode) *AVLTreeNode {
    node.Left = LeftRotation(node.Left)
    return RightRotation(node)
}

直接复用了之前左旋和右旋的代码，虽然难以理解，但是画一下图，确实这样调整后树高度降了，不再失衡，一切 perfect。

3.4. 右子树插左儿子：先右后左旋

在右子树上插上左儿子导致失衡，先右后左旋：

代码如下：

// 先右后左旋操作，看图说话
func RightLeftRotation(node *AVLTreeNode) *AVLTreeNode {
    node.Right = RightRotation(node.Right)
    return LeftRotation(node)
}

3.5. 具体实现

四种旋转代码实现后，我们开始进行添加元素操作：

// 添加元素
func (tree *AVLTree) Add(value int64) {
    // 往树根添加元素，会返回新的树根
    tree.Root = tree.Root.Add(value)
}
func (node *AVLTreeNode) Add(value int64) *AVLTreeNode {
    // 添加值到根节点node，如果node为空，那么让值成为新的根节点，树的高度为1
    if node == nil {
        return &AVLTreeNode{Value: value, Height: 1}
    }
    // 如果值重复，什么都不用做，直接更新次数
    if node.Value == value {
        node.Times = node.Times + 1
        return node
    }
    // 辅助变量
    var newTreeNode *AVLTreeNode
    if value > node.Value {
        // 插入的值大于节点值，要从右子树继续插入
        node.Right = node.Right.Add(value)
        // 平衡因子，插入右子树后，要确保树根左子树的高度不能比右子树低一层。
        factor := node.BalanceFactor()
        // 右子树的高度变高了，导致左子树-右子树的高度从-1变成了-2。
        if factor == -2 {
            if value > node.Right.Value {
                // 表示在右子树上插上右儿子导致失衡，需要单左旋：
                newTreeNode = LeftRotation(node)
            } else {
                //表示在右子树上插上左儿子导致失衡，先右后左旋：
                newTreeNode = RightLeftRotation(node)
            }
        }
    } else {
        // 插入的值小于节点值，要从左子树继续插入
        node.Left = node.Left.Add(value)
        // 平衡因子，插入左子树后，要确保树根左子树的高度不能比右子树高一层。
        factor := node.BalanceFactor()
        // 左子树的高度变高了，导致左子树-右子树的高度从1变成了2。
        if factor == 2 {
            if value < node.Left.Value {
                // 表示在左子树上插上左儿子导致失衡，需要单右旋：
                newTreeNode = RightRotation(node)
            } else {
                //表示在左子树上插上右儿子导致失衡，先左后右旋：
                newTreeNode = LeftRightRotation(node)
            }
        }
    }
    if newTreeNode == nil {
        // 表示什么旋转都没有，根节点没变，直接刷新树高度
        node.UpdateHeight()
        return node
    } else {
        // 旋转了，树根节点变了，需要刷新新的树根高度
        newTreeNode.UpdateHeight()
        return newTreeNode
    }
}

一开始从树根节点开始插入新值：tree.Root = tree.Root.Add(value)，因为插入值后会返回新的根节点，也就是说调整过程中树根节点会变化，所以要重新将新根节点赋予老的根节点。

在 func (node *AVLTreeNode) Add(value int64) 函数中，如果根节点为空，那么需要返回新的根节点：

1. // 添加值到根节点node，如果node为空，那么让值成为新的根节点，树的高度为1
2. if node == nil {
3. return &AVLTreeNode{Value: value, Height: 1}
4. }

接着，如果插入的值和节点的值一样，直接更新 Times：

1. // 如果值重复，什么都不用做，直接更新次数
2. if node.Value == value {
3. node.Times = node.Times + 1
4. return node
5. }

否则根据值的大小，旋转插入到左子树或右子树，我们只分析插入右子树的代码：

1. if value > node.Value {
2. // 插入的值大于节点值，要从右子树继续插入
3. node.Right = node.Right.Add(value)
4. // 平衡因子，插入右子树后，要确保树根左子树的高度不能比右子树低一层。
5. factor := node.BalanceFactor()
6. // 右子树的高度变高了，导致左子树-右子树的高度从-1变成了-2。
7. if factor == -2 {
8. if value > node.Right.Value {
9. // 表示在右子树上插上右儿子导致失衡，需要单左旋：
10. newTreeNode = LeftRotation(node)
11. } else {
12. //表示在右子树上插上左儿子导致失衡，先右后左旋：
13. newTreeNode = RightLeftRotation(node)
14. }
15. }
16. }

因为值添加到了右子树，所以转换成了在右子树添加元素：node.Right = node.Right.Add(value)，之后要判断根节点的平衡因子是否变化了。

值插入右子树后，要确保树根左子树的高度不能比右子树低一层。当平衡因子 factor == -2 表示右子树的高度变高了，导致 左子树-右子树 的高度从 -1 变成了 -2，所以要旋转。

判断新插入的值是在右子树的左儿子还是右儿子上：

1. if value > node.Right.Value {
2. // 表示在右子树上插上右儿子导致失衡，需要单左旋：
3. newTreeNode = LeftRotation(node)
4. } else {
5. //表示在右子树上插上左儿子导致失衡，先右后左旋：
6. newTreeNode = RightLeftRotation(node)
7. }

如果在右子树上插上右儿子导致失衡，需要单左旋：LeftRotation(node)，如果在右子树上插上左儿子导致失衡，先右后左旋：RightLeftRotation(node)。

最后需要更新树根节点的高度，并返回树根(如果曾经旋转，表示树根变了，需要返回新的树根)：

1. if newTreeNode == nil {
2. // 表示什么旋转都没有，根节点没变，直接刷新树高度
3. node.UpdateHeight()
4. return node
5. } else {
6. // 旋转了，树根节点变了，需要刷新新的树根高度
7. newTreeNode.UpdateHeight()
8. return newTreeNode
9. }

3.6. 时间复杂度分析

添加元素时先要找到元素插入的位置，找到位置后逐层自底向上更新每个子树的树高度，并根据子树平衡是否被破坏，需要进行旋转操作。

由于树的高度最高为 1.44log(n)，查找元素插入位置，最坏次数为 1.44log(n) 次。逐层更新子树高度并判断平衡是否被破坏，最坏需要 1.44log(n) 次，因此可以得知添加元素最坏时间复杂度为：2.88log(n)，去掉常数项，时间复杂度为：log(n)。

关于旋转次数，当插入节点后，某子树不平衡时最多旋转 2次，也就是双旋该子树即可恢复平衡，该调整为局部特征，调整完后其父层不再需要旋转。也就是说，插入操作最坏旋转两次即可。

由于代码的递归实现方式，当某子树旋转过后其父层子树仍然需要判断平衡因子，判断是否需要旋转，该操作是不必要的，因为子树旋转过后全局已经平衡了，不必再判断父层的平衡因子。

对此可以进行代码优化，在左子树或右子树插入元素后，除了返回根节点，还返回其是否旋转过的辅助变量，如：func (node *AVLTreeNode) Add(value int64) (newNode *AVLTreeNode, rotate bool) ，根据返回的辅助变量 rotate，可以：

1. node.Right, rotate= node.Right.Add(value)
2. if !rotate {
3. // 子树没有旋转过，那么需要判断是否需要旋转
5. // 平衡因子，插入右子树后，要确保树根左子树的高度不能比右子树低一层。
6. factor := node.BalanceFactor()
7. // 右子树的高度变高了，导致左子树-右子树的高度从-1变成了-2。
8. if factor == -2 {
9. if value > node.Right.Value {
10. // 表示在右子树上插上右儿子导致失衡，需要单左旋：
11. newTreeNode = LeftRotation(node)
12. } else {
13. //表示在右子树上插上左儿子导致失衡，先右后左旋：
14. newTreeNode = RightLeftRotation(node)
15. }
16. }
17. }else{
18. // do nothing
19. }

但此优化意义不大，因为返回辅助变量后仍然需要判断，判断辅助变量和判断平衡因子，时间复杂度一样。

插入元素进行调整后，需要递归向上更新每一棵子树高度，其时间复杂度为 log(n)，但可以优化，当两棵子树高度都没有变化时，那么上面的父层子树们都不需要更新树高度，直接退出，由于是递归程序，如何向上传递这个信息，引入了额外空间成本，且不可避免仍然会出现所有层级的父节点都必须更新树高度，优化意义不是很大。

四、AVL树查找元素等操作

其他操作与二叉查找树通用，代码如下：

// 找出最小值的节点
func (tree *AVLTree) FindMinValue() *AVLTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMinValue()
}
func (node *AVLTreeNode) FindMinValue() *AVLTreeNode {
    // 左子树为空，表面已经是最左的节点了，该值就是最小值
    if node.Left == nil {
        return node
    }
    // 一直左子树递归
    return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *AVLTree) FindMaxValue() *AVLTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMaxValue()
}
func (node *AVLTreeNode) FindMaxValue() *AVLTreeNode {
    // 右子树为空，表面已经是最右的节点了，该值就是最大值
    if node.Right == nil {
        return node
    }
    // 一直右子树递归
    return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *AVLTree) Find(value int64) *AVLTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.Find(value)
}
func (node *AVLTreeNode) Find(value int64) *AVLTreeNode {
    if value == node.Value {
        // 如果该节点刚刚等于该值，那么返回该节点
        return node
    } else if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        if node.Left == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Left.Find(value)
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        if node.Right == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Right.Find(value)
    }
}
// 中序遍历
func (tree *AVLTree) MidOrder() {
    tree.Root.MidOrder()
}
func (node *AVLTreeNode) MidOrder() {
    if node == nil {
        return
    }
    // 先打印左子树
    node.Left.MidOrder()
    // 按照次数打印根节点
    for i := 0; i <= int(node.Times); i++ {
        fmt.Println(node.Value)
    }
    // 打印右子树
    node.Right.MidOrder()
}

查找操作逻辑与通用的二叉查找树一样，并无区别。

五、AVL树删除元素

删除元素有四种情况：

1. 删除的节点是叶子节点，没有儿子，直接删除后看离它最近的父亲节点是否失衡，做调整操作。
2. 删除的节点下有两个子树，选择高度更高的子树下的节点来替换被删除的节点，如果左子树更高，选择左子树中最大的节点，也就是左子树最右边的叶子节点，如果右子树更高，选择右子树中最小的节点，也就是右子树最左边的叶子节点。最后，删除这个叶子节点，也就是变成情况1。
3. 删除的节点只有左子树，可以知道左子树其实就只有一个节点，被删除节点本身（假设左子树多于2个节点，那么高度差就等于2了，不符合AVL树定义），将左节点替换被删除的节点，最后删除这个左节点，变成情况1。
4. 删除的节点只有右子树，可以知道右子树其实就只有一个节点，被删除节点本身（假设右子树多于2个节点，那么高度差就等于2了，不符合AVL树定义），将右节点替换被删除的节点，最后删除这个右节点，变成情况1。

后面三种情况最后都变成 情况1，就是将删除的节点变成叶子节点，然后可以直接删除该叶子节点，然后看其最近的父亲节点是否失衡，失衡时对树进行平衡。

举个例子，删除叶子节点，如图：

删除节点 24，导致节点 26 的子树不平衡了，这时需要对该子树进行旋转，旋转后如图：

可以发现这时树仍然不平衡，这时是节点 22 的子树不平衡，需要继续旋转，旋转后如图：

实现代码如下：

func (node *AVLTreeNode) Delete(value int64) *AVLTreeNode {
    if node == nil {
        // 如果是空树，直接返回
        return nil
    }
    if value < node.Value {
        // 从左子树开始删除
        node.Left = node.Left.Delete(value)
        // 删除后要更新该子树高度
        node.Left.UpdateHeight()
    } else if value > node.Value {
        // 从右子树开始删除
        node.Right = node.Right.Delete(value)
        // 删除后要更新该子树高度
        node.Right.UpdateHeight()
    } else {
        // 找到该值对应的节点
        // 该节点没有左右子树
        // 第一种情况，删除的节点没有儿子，直接删除即可。
        if node.Left == nil && node.Right == nil {
            return nil // 直接返回nil，表示直接该值删除
        }
        // 该节点有两棵子树，选择更高的哪个来替换
        // 第二种情况，删除的节点下有两个子树，选择高度更高的子树下的节点来替换被删除的节点，如果左子树更高，选择左子树中最大的节点，也就是左子树最右边的叶子节点，如果右子树更高，选择右子树中最小的节点，也就是右子树最左边的叶子节点。最后，删除这个叶子节点。
        if node.Left != nil && node.Right != nil {
            // 左子树更高，拿左子树中最大值的节点替换
            if node.Left.Height > node.Right.Height {
                maxNode := node.Left
                for maxNode.Right != nil {
                    maxNode = maxNode.Right
                }
                // 最大值的节点替换被删除节点
                node.Value = maxNode.Value
                node.Times = maxNode.Times
                // 把最大的节点删掉
                node.Left = node.Left.Delete(maxNode.Value)
                // 删除后要更新该子树高度
                node.Left.UpdateHeight()
            } else {
                // 右子树更高，拿右子树中最小值的节点替换
                minNode := node.Right
                for minNode.Left != nil {
                    minNode = minNode.Left
                }
                // 最小值的节点替换被删除节点
                node.Value = minNode.Value
                node.Times = minNode.Times
                // 把最小的节点删掉
                node.Right = node.Right.Delete(minNode.Value)
                // 删除后要更新该子树高度
                node.Right.UpdateHeight()
            }
        } else {
            // 只有左子树或只有右子树
            // 只有一个子树，该子树也只是一个节点，将该节点替换被删除的节点，然后置子树为空
            if node.Left != nil {
                //第三种情况，删除的节点只有左子树，因为树的特征，可以知道左子树其实就只有一个节点，它本身，否则高度差就等于2了。
                node.Value = node.Left.Value
                node.Times = node.Left.Times
                node.Height = 1
                node.Left = nil
            } else if node.Right != nil {
                //第四种情况，删除的节点只有右子树，因为树的特征，可以知道右子树其实就只有一个节点，它本身，否则高度差就等于2了。
                node.Value = node.Right.Value
                node.Times = node.Right.Times
                node.Height = 1
                node.Right = nil
            }
        }
        // 找到值后，进行替换删除后，直接返回该节点
        return node
    }
    // 左右子树递归删除节点后需要平衡
    var newNode *AVLTreeNode
    // 相当删除了右子树的节点，左边比右边高了，不平衡
    if node.BalanceFactor() == 2 {
        if node.Left.BalanceFactor() >= 0 {
            newNode = RightRotation(node)
        } else {
            newNode = LeftRightRotation(node)
        }
        //  相当删除了左子树的节点，右边比左边高了，不平衡
    } else if node.BalanceFactor() == -2 {
        if node.Right.BalanceFactor() <= 0 {
            newNode = LeftRotation(node)
        } else {
            newNode = RightLeftRotation(node)
        }
    }
    if newNode == nil {
        node.UpdateHeight()
        return node
    } else {
        newNode.UpdateHeight()
        return newNode
    }
}

当删除的值不等于当前节点的值时，在相应的子树中递归删除，递归过程中会自底向上维护AVL树的特征。

1. 小于删除的值 value < node.Value，在左子树中递归删除：node.Left = node.Left.Delete(value)。
2. 大于删除的值 value > node.Value，在右子树中递归删除：node.Right = node.Right.Delete(value)。

因为删除后可能因为旋转调整，导致树根节点变了，这时会返回新的树根，递归删除后需要将返回的新根节点赋予原来的老根节点。

情况1，找到要删除的值时，该值是叶子节点，直接删除该节点即可：

1. // 第一种情况，删除的节点没有儿子，直接删除即可。
2. if node.Left == nil && node.Right == nil {
3. return nil // 直接返回nil，表示直接该值删除
4. }

情况2，删除的节点有两棵子树，选择高度更高的子树下的节点来替换被删除的节点：

1. // 该节点有两棵子树，选择更高的哪个来替换
2. // 第二种情况，删除的节点下有两个子树，选择高度更高的子树下的节点来替换被删除的节点，如果左子树更高，选择左子树中最大的节点，也就是左子树最右边的叶子节点，如果右子树更高，选择右子树中最小的节点，也就是右子树最左边的叶子节点。最后，删除这个叶子节点。
3. if node.Left != nil && node.Right != nil {
4. // 左子树更高，拿左子树中最大值的节点替换
5. if node.Left.Height > node.Right.Height {
6. maxNode := node.Left
7. for maxNode.Right != nil {
8. maxNode = maxNode.Right
9. }
11. // 最大值的节点替换被删除节点
12. node.Value = maxNode.Value
13. node.Times = maxNode.Times
15. // 把最大的节点删掉
16. node.Left = node.Left.Delete(maxNode.Value)
17. // 删除后要更新该子树高度
18. node.Left.UpdateHeight()
19. } else {
20. // 右子树更高，拿右子树中最小值的节点替换
21. minNode := node.Right
22. for minNode.Left != nil {
23. minNode = minNode.Left
24. }
26. // 最小值的节点替换被删除节点
27. node.Value = minNode.Value
28. node.Times = minNode.Times
30. // 把最小的节点删掉
31. node.Right = node.Right.Delete(minNode.Value)
32. // 删除后要更新该子树高度
33. node.Right.UpdateHeight()
34. }
35. }

情况3和情况4，如果被删除的节点只有一个子树，那么该子树一定没有儿子，不然树的高度就大于1了，所以直接替换值后删除该子树节点：

1. // 只有左子树或只有右子树
2. // 只有一个子树，该子树也只是一个节点，将该节点替换被删除的节点，然后置子树为空
3. if node.Left != nil {
4. //第三种情况，删除的节点只有左子树，因为树的特征，可以知道左子树其实就只有一个节点，它本身，否则高度差就等于2了。
5. node.Value = node.Left.Value
6. node.Times = node.Left.Times
7. node.Height = 1
8. node.Left = nil
9. } else if node.Right != nil {
10. //第四种情况，删除的节点只有右子树，因为树的特征，可以知道右子树其实就只有一个节点，它本身，否则高度差就等于2了。
11. node.Value = node.Right.Value
12. node.Times = node.Right.Times
13. node.Height = 1
14. node.Right = nil
15. }

核心在于删除后的旋转调整，如果删除的值不匹配当前节点的值，对当前节点的左右子树进行递归删除，递归删除后该节点为根节点的子树可能不平衡，我们需要判断后决定要不要旋转这棵树。

每次递归都是自底向上，从很小的子树到很大的子树，如果自底向上每棵子树都进行调整，约束在树的高度差不超过1，那么整棵树自然也符合AVL树的平衡规则。

删除元素后，如果子树失衡，需要进行调整操作，主要有两种：删除后左子树比右子树高，删除后右子树比左子树高。

5.1. 删除后，左子树比右子树高

如果删除了右子树的节点，左边比右边高了，不平衡了：

1. // 相当删除了右子树的节点，左边比右边高了，不平衡
2. if node.BalanceFactor() == 2 {
3. if node.Left.BalanceFactor() >= 0 {
4. newNode = RightRotation(node)
5. } else {
6. newNode = LeftRightRotation(node)
7. }
8. }

为什么要这么调整呢，看图说话，有两幅图参考：

这幅图可以看到：

1. 黄色点5.BalanceFactor() == 2，对应：node.BalanceFactor() == 2。
2. 绿色点3.BalanceFactor() == 1，对应：node.Left.BalanceFactor() == 1。

所以应该需要右旋：newNode = RightRotation(node)

这幅图可以看到：

1. 黄色点5.BalanceFactor() == 2，对应：node.BalanceFactor() == 2
2. 绿色点3.BalanceFactor() == -1，对应：node.Left.BalanceFactor() == -1。

所以应该需要先左后右旋：newNode = LeftRightRotation(node)

还有一种特殊情况，和上面的都不一样，如图：

我们如果删除节点 22 或节点 23，这个时候根节点 20 失衡了。

1. 根节点 20 的左子树比右子树高了 2 层，对应：node.BalanceFactor() == 2。
2. 左子树节点 13 并没有失衡，对应：node.BalanceFactor() == 0。

这个时候，无论使用右旋，还是先左旋后右旋都可以使树恢复平衡，我们的 if 判断条件使用了右旋。

如果是先左旋后右旋，那么旋转后恢复平衡，如图对根结点进行旋转：

如果使用右旋也可以，如图对根结点进行旋转：

5.2. 删除后，右子树比左子树高

如果删除了左子树的节点，右边比左边高了，不平衡了：

        //  相当删除了左子树的节点，右边比左边高了，不平衡
        if node.BalanceFactor() == -2 {
            if node.Right.BalanceFactor() <= 0 {
            newNode = LeftRotation(node)
            } else {
            newNode = RightLeftRotation(node)
            }
        }

为什么要这么调整呢，看图说话，有两幅图参考：

这幅图可以看到：

1. 绿色点3.BalanceFactor() == -2，对应：node.BalanceFactor() == -2。
2. 黄色点5.BalanceFactor() == -1，对应：node.Left.BalanceFactor() == -1。

所以应该需要左旋：newNode = LeftRotation(node)

这幅图可以看到：

1. 绿色点3.BalanceFactor() == -2，对应：node.BalanceFactor() == -2。
2. 黄色点5.BalanceFactor() == 1，对应：node.Left.BalanceFactor() == 1。

所以应该需要先右后左旋：newNode = RightLeftRotation(node)

当然，还有另外一种特殊情况，与 5.1 章节类似，使用左旋还是先右旋后左旋都可以，在这里就不阐述了。

5.3. 删除后，调整树高度

进行调整操作后，需要更新该子树的高度。如果没有旋转过，更新之前节点的树高度。如果曾经旋转过，树根变了，更新新的树根节点高度。

1. if newNode == nil {
2. node.UpdateHeight()
3. return node
4. } else {
5. newNode.UpdateHeight()
6. return newNode
7. }

5.4. 时间复杂度分析

删除操作是先找到删除的节点，然后将该节点与一个叶子节点交换，接着删除叶子节点，最后对叶子节点的父层逐层向上旋转调整。

删除操作的时间复杂度和添加操作一样。区别在于，添加操作最多旋转两次就可以达到树的平衡，而删除操作可能会旋转超过两次。

如图是一棵比较糟糕的 AVL 树：

删除节点1，旋转可以一直旋转到根节点，比插入旋转最多旋转两次的次数更多。

六、验证是否是一棵AVL树

如何确保我们的代码实现的就是一棵 AVL 树呢，可以进行验证：

// 验证是不是棵AVL树
func (tree *AVLTree) IsAVLTree() bool {
    if tree == nil || tree.Root == nil {
        return true
    }
    // 判断节点是否符合 AVL 树的定义
    if tree.Root.IsRight() {
        return true
    }
    return false
}
// 判断节点是否符合 AVL 树的定义
func (node *AVLTreeNode) IsRight() bool {
    if node == nil {
        return true
    }
    // 左右子树都为空，那么是叶子节点
    if node.Left == nil && node.Right == nil {
        // 叶子节点高度应该为1
        if node.Height == 1 {
            return true
        } else {
            fmt.Println("leaf node height is ", node.Height)
            return false
        }
    } else if node.Left != nil && node.Right != nil {
        // 左右子树都是满的
        // 左儿子必须比父亲小，右儿子必须比父亲大
        if node.Left.Value < node.Value && node.Right.Value > node.Value {
        } else {
            // 不符合 AVL 树定义
            fmt.Printf("father is %v lchild is %v, rchild is %v\n", node.Value, node.Left.Value, node.Right.Value)
            return false
        }
        bal := node.Left.Height - node.Right.Height
        if bal < 0 {
            bal = -bal
        }
        // 子树高度差不能大于1
        if bal > 1 {
            fmt.Println("sub tree height bal is ", bal)
            return false
        }
        // 如果左子树比右子树高，那么父亲的高度等于左子树+1
        if node.Left.Height > node.Right.Height {
            if node.Height == node.Left.Height+1 {
            } else {
                fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
                return false
            }
        } else {
            // 如果右子树比左子树高，那么父亲的高度等于右子树+1
            if node.Height == node.Right.Height+1 {
            } else {
                fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
                return false
            }
        }
        // 递归判断子树
        if !node.Left.IsRight() {
            return false
        }
        // 递归判断子树
        if !node.Right.IsRight() {
            return false
        }
    } else {
        // 只存在一棵子树
        if node.Right != nil {
            // 子树高度只能是1
            if node.Right.Height == 1 && node.Right.Left == nil && node.Right.Right == nil {
                if node.Right.Value > node.Value {
                    // 右节点必须比父亲大
                } else {
                    fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                    return false
                }
            } else {
                fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                return false
            }
        } else {
            if node.Left.Height == 1 && node.Left.Left == nil && node.Left.Right == nil {
                if node.Left.Value < node.Value {
                    // 左节点必须比父亲小
                } else {
                    fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                    return false
                }
            } else {
                fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                return false
            }
        }
    }
    return true
}

七、AVL树完整代码

package main
import (
    "fmt"
)
// AVL树
type AVLTree struct {
    Root *AVLTreeNode // 树根节点
}
// AVL节点
type AVLTreeNode struct {
    Value  int64        // 值
    Times  int64        // 值出现的次数
    Height int64        // 该节点作为树根节点，树的高度，方便计算平衡因子
    Left   *AVLTreeNode // 左子树
    Right  *AVLTreeNode // 右字树
}
// 初始化一个AVL树
func NewAVLTree() *AVLTree {
    return new(AVLTree)
}
// 更新节点的树高度
func (node *AVLTreeNode) UpdateHeight() {
    if node == nil {
        return
    }
    var leftHeight, rightHeight int64 = 0, 0
    if node.Left != nil {
        leftHeight = node.Left.Height
    }
    if node.Right != nil {
        rightHeight = node.Right.Height
    }
    // 哪个子树高算哪棵的
    maxHeight := leftHeight
    if rightHeight > maxHeight {
        maxHeight = rightHeight
    }
    // 高度加上自己那一层
    node.Height = maxHeight + 1
}
// 计算平衡因子
func (node *AVLTreeNode) BalanceFactor() int64 {
    var leftHeight, rightHeight int64 = 0, 0
    if node.Left != nil {
        leftHeight = node.Left.Height
    }
    if node.Right != nil {
        rightHeight = node.Right.Height
    }
    return leftHeight - rightHeight
}
// 单右旋操作，看图说话
func RightRotation(Root *AVLTreeNode) *AVLTreeNode {
    // 只有Pivot和B，Root位置变了
    Pivot := Root.Left
    B := Pivot.Right
    Pivot.Right = Root
    Root.Left = B
    // 只有Root和Pivot变化了高度
    Root.UpdateHeight()
    Pivot.UpdateHeight()
    return Pivot
}
// 单左旋操作，看图说话
func LeftRotation(Root *AVLTreeNode) *AVLTreeNode {
    // 只有Pivot和B，Root位置变了
    Pivot := Root.Right
    B := Pivot.Left
    Pivot.Left = Root
    Root.Right = B
    // 只有Root和Pivot变化了高度
    Root.UpdateHeight()
    Pivot.UpdateHeight()
    return Pivot
}
// 先左后右旋操作，看图说话
func LeftRightRotation(node *AVLTreeNode) *AVLTreeNode {
    node.Left = LeftRotation(node.Left)
    return RightRotation(node)
}
// 先右后左旋操作，看图说话
func RightLeftRotation(node *AVLTreeNode) *AVLTreeNode {
    node.Right = RightRotation(node.Right)
    return LeftRotation(node)
}
// 添加元素
func (tree *AVLTree) Add(value int64) {
    // 往树根添加元素，会返回新的树根
    tree.Root = tree.Root.Add(value)
}
func (node *AVLTreeNode) Add(value int64) *AVLTreeNode {
    // 添加值到根节点node，如果node为空，那么让值成为新的根节点，树的高度为1
    if node == nil {
        return &AVLTreeNode{Value: value, Height: 1}
    }
    // 如果值重复，什么都不用做，直接更新次数
    if node.Value == value {
        node.Times = node.Times + 1
        return node
    }
    // 辅助变量
    var newTreeNode *AVLTreeNode
    if value > node.Value {
        // 插入的值大于节点值，要从右子树继续插入
        node.Right = node.Right.Add(value)
        // 平衡因子，插入右子树后，要确保树根左子树的高度不能比右子树低一层。
        factor := node.BalanceFactor()
        // 右子树的高度变高了，导致左子树-右子树的高度从-1变成了-2。
        if factor == -2 {
            if value > node.Right.Value {
                // 表示在右子树上插上右儿子导致失衡，需要单左旋：
                newTreeNode = LeftRotation(node)
            } else {
                //表示在右子树上插上左儿子导致失衡，先右后左旋：
                newTreeNode = RightLeftRotation(node)
            }
        }
    } else {
        // 插入的值小于节点值，要从左子树继续插入
        node.Left = node.Left.Add(value)
        // 平衡因子，插入左子树后，要确保树根左子树的高度不能比右子树高一层。
        factor := node.BalanceFactor()
        // 左子树的高度变高了，导致左子树-右子树的高度从1变成了2。
        if factor == 2 {
            if value < node.Left.Value {
                // 表示在左子树上插上左儿子导致失衡，需要单右旋：
                newTreeNode = RightRotation(node)
            } else {
                //表示在左子树上插上右儿子导致失衡，先左后右旋：
                newTreeNode = LeftRightRotation(node)
            }
        }
    }
    if newTreeNode == nil {
        // 表示什么旋转都没有，根节点没变，直接刷新树高度
        node.UpdateHeight()
        return node
    } else {
        // 旋转了，树根节点变了，需要刷新新的树根高度
        newTreeNode.UpdateHeight()
        return newTreeNode
    }
}
// 找出最小值的节点
func (tree *AVLTree) FindMinValue() *AVLTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMinValue()
}
func (node *AVLTreeNode) FindMinValue() *AVLTreeNode {
    // 左子树为空，表面已经是最左的节点了，该值就是最小值
    if node.Left == nil {
        return node
    }
    // 一直左子树递归
    return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *AVLTree) FindMaxValue() *AVLTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMaxValue()
}
func (node *AVLTreeNode) FindMaxValue() *AVLTreeNode {
    // 右子树为空，表面已经是最右的节点了，该值就是最大值
    if node.Right == nil {
        return node
    }
    // 一直右子树递归
    return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *AVLTree) Find(value int64) *AVLTreeNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.Find(value)
}
func (node *AVLTreeNode) Find(value int64) *AVLTreeNode {
    if value == node.Value {
        // 如果该节点刚刚等于该值，那么返回该节点
        return node
    } else if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        if node.Left == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Left.Find(value)
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        if node.Right == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Right.Find(value)
    }
}
// 删除指定的元素
func (tree *AVLTree) Delete(value int64) {
    if tree.Root == nil {
        // 如果是空树，直接返回
        return
    }
    tree.Root = tree.Root.Delete(value)
}
func (node *AVLTreeNode) Delete(value int64) *AVLTreeNode {
    if node == nil {
        // 如果是空树，直接返回
        return nil
    }
    if value < node.Value {
        // 从左子树开始删除
        node.Left = node.Left.Delete(value)
        // 删除后要更新该子树高度
        node.Left.UpdateHeight()
    } else if value > node.Value {
        // 从右子树开始删除
        node.Right = node.Right.Delete(value)
        // 删除后要更新该子树高度
        node.Right.UpdateHeight()
    } else {
        // 找到该值对应的节点
        // 该节点没有左右子树
        // 第一种情况，删除的节点没有儿子，直接删除即可。
        if node.Left == nil && node.Right == nil {
            return nil // 直接返回nil，表示直接该值删除
        }
        // 该节点有两棵子树，选择更高的哪个来替换
        // 第二种情况，删除的节点下有两个子树，选择高度更高的子树下的节点来替换被删除的节点，如果左子树更高，选择左子树中最大的节点，也就是左子树最右边的叶子节点，如果右子树更高，选择右子树中最小的节点，也就是右子树最左边的叶子节点。最后，删除这个叶子节点。
        if node.Left != nil && node.Right != nil {
            // 左子树更高，拿左子树中最大值的节点替换
            if node.Left.Height > node.Right.Height {
                maxNode := node.Left
                for maxNode.Right != nil {
                    maxNode = maxNode.Right
                }
                // 最大值的节点替换被删除节点
                node.Value = maxNode.Value
                node.Times = maxNode.Times
                // 把最大的节点删掉
                node.Left = node.Left.Delete(maxNode.Value)
                // 删除后要更新该子树高度
                node.Left.UpdateHeight()
            } else {
                // 右子树更高，拿右子树中最小值的节点替换
                minNode := node.Right
                for minNode.Left != nil {
                    minNode = minNode.Left
                }
                // 最小值的节点替换被删除节点
                node.Value = minNode.Value
                node.Times = minNode.Times
                // 把最小的节点删掉
                node.Right = node.Right.Delete(minNode.Value)
                // 删除后要更新该子树高度
                node.Right.UpdateHeight()
            }
        } else {
            // 只有左子树或只有右子树
            // 只有一个子树，该子树也只是一个节点，将该节点替换被删除的节点，然后置子树为空
            if node.Left != nil {
                //第三种情况，删除的节点只有左子树，因为树的特征，可以知道左子树其实就只有一个节点，它本身，否则高度差就等于2了。
                node.Value = node.Left.Value
                node.Times = node.Left.Times
                node.Height = 1
                node.Left = nil
            } else if node.Right != nil {
                //第四种情况，删除的节点只有右子树，因为树的特征，可以知道右子树其实就只有一个节点，它本身，否则高度差就等于2了。
                node.Value = node.Right.Value
                node.Times = node.Right.Times
                node.Height = 1
                node.Right = nil
            }
        }
        // 找到值后，进行替换删除后，直接返回该节点
        return node
    }
    // 左右子树递归删除节点后需要平衡
    var newNode *AVLTreeNode
    // 相当删除了右子树的节点，左边比右边高了，不平衡
    if node.BalanceFactor() == 2 {
        if node.Left.BalanceFactor() >= 0 {
            newNode = RightRotation(node)
        } else {
            newNode = LeftRightRotation(node)
        }
        //  相当删除了左子树的节点，右边比左边高了，不平衡
    } else if node.BalanceFactor() == -2 {
        if node.Right.BalanceFactor() <= 0 {
            newNode = LeftRotation(node)
        } else {
            newNode = RightLeftRotation(node)
        }
    }
    if newNode == nil {
        node.UpdateHeight()
        return node
    } else {
        newNode.UpdateHeight()
        return newNode
    }
}
// 中序遍历
func (tree *AVLTree) MidOrder() {
    tree.Root.MidOrder()
}
func (node *AVLTreeNode) MidOrder() {
    if node == nil {
        return
    }
    // 先打印左子树
    node.Left.MidOrder()
    // 按照次数打印根节点
    for i := 0; i <= int(node.Times); i++ {
        fmt.Println("value:", node.Value, " tree height:", node.BalanceFactor())
    }
    // 打印右子树
    node.Right.MidOrder()
}
// 验证是不是棵AVL树
func (tree *AVLTree) IsAVLTree() bool {
    if tree == nil || tree.Root == nil {
        return true
    }
    // 判断节点是否符合 AVL 树的定义
    if tree.Root.IsRight() {
        return true
    }
    return false
}
// 判断节点是否符合 AVL 树的定义
func (node *AVLTreeNode) IsRight() bool {
    if node == nil {
        return true
    }
    // 左右子树都为空，那么是叶子节点
    if node.Left == nil && node.Right == nil {
        // 叶子节点高度应该为1
        if node.Height == 1 {
            return true
        } else {
            fmt.Println("leaf node height is ", node.Height)
            return false
        }
    } else if node.Left != nil && node.Right != nil {
        // 左右子树都是满的
        // 左儿子必须比父亲小，右儿子必须比父亲大
        if node.Left.Value < node.Value && node.Right.Value > node.Value {
        } else {
            // 不符合 AVL 树定义
            fmt.Printf("father is %v lchild is %v, rchild is %v\n", node.Value, node.Left.Value, node.Right.Value)
            return false
        }
        bal := node.Left.Height - node.Right.Height
        if bal < 0 {
            bal = -bal
        }
        // 子树高度差不能大于1
        if bal > 1 {
            fmt.Println("sub tree height bal is ", bal)
            return false
        }
        // 如果左子树比右子树高，那么父亲的高度等于左子树+1
        if node.Left.Height > node.Right.Height {
            if node.Height == node.Left.Height+1 {
            } else {
                fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
                return false
            }
        } else {
            // 如果右子树比左子树高，那么父亲的高度等于右子树+1
            if node.Height == node.Right.Height+1 {
            } else {
                fmt.Printf("%#v height:%v,left sub tree height: %v,right sub tree height:%v\n", node, node.Height, node.Left.Height, node.Right.Height)
                return false
            }
        }
        // 递归判断子树
        if !node.Left.IsRight() {
            return false
        }
        // 递归判断子树
        if !node.Right.IsRight() {
            return false
        }
    } else {
        // 只存在一棵子树
        if node.Right != nil {
            // 子树高度只能是1
            if node.Right.Height == 1 && node.Right.Left == nil && node.Right.Right == nil {
                if node.Right.Value > node.Value {
                    // 右节点必须比父亲大
                } else {
                    fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                    return false
                }
            } else {
                fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                return false
            }
        } else {
            if node.Left.Height == 1 && node.Left.Left == nil && node.Left.Right == nil {
                if node.Left.Value < node.Value {
                    // 左节点必须比父亲小
                } else {
                    fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                    return false
                }
            } else {
                fmt.Printf("%v,(%#v,%#v) child", node.Value, node.Right, node.Left)
                return false
            }
        }
    }
    return true
}
func main() {
    values := []int64{2, 3, 7, 10, 10, 10, 10, 23, 9, 102, 109, 111, 112, 113}
    // 初始化二叉查找树并添加元素
    tree := NewAVLTree()
    for _, v := range values {
        tree.Add(v)
    }
    // 找到最大值或最小值的节点
    fmt.Println("find min value:", tree.FindMinValue())
    fmt.Println("find max value:", tree.FindMaxValue())
    // 查找不存在的99
    node := tree.Find(99)
    if node != nil {
        fmt.Println("find it 99!")
    } else {
        fmt.Println("not find it 99!")
    }
    // 查找存在的9
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    // 删除存在的9后，再查找9
    tree.Delete(9)
    tree.Delete(10)
    tree.Delete(2)
    tree.Delete(3)
    tree.Add(4)
    tree.Add(3)
    tree.Add(10)
    tree.Delete(111)
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    // 中序遍历，实现排序
    tree.MidOrder()
    if tree.IsAVLTree() {
        fmt.Println("is a avl tree")
    } else {
        fmt.Println("is not avl tree")
    }
}

PS：我们的程序是递归程序，如果改写为非递归形式，效率和性能会更好，在此就不实现了，理解AVL树添加和删除的总体思路即可。

八、应用场景

AVL 树作为严格平衡的二叉查找树，在 windows 对进程地址空间的管理被使用到。

2-3树和左倾红黑树

某些教程不区分普通红黑树和左倾红黑树的区别，直接将左倾红黑树拿来教学，并且称其为红黑树，因为左倾红黑树与普通的红黑树相比，实现起来较为简单，容易教学。在这里，我们区分开左倾红黑树和普通红黑树。

红黑树是一种近似平衡的二叉查找树，从 2-3 树或 2-3-4 树衍生而来。通过对二叉树节点进行染色，染色为红或黑节点，来模仿 2-3 树或 2-3-4 树的3节点和4节点，从而让树的高度减小。2-3-4 树对照实现的红黑树是普通的红黑树，而 2-3 树对照实现的红黑树是一种变种，称为左倾红黑树，其更容易实现。

使用平衡树数据结构，可以提高查找元素的速度，我们在本章介绍 2-3 树，再用二叉树形式来实现 2-3 树，也就是左倾红黑树。

一、2-3 树

1.1. 2-3 树介绍

2-3 树是一棵严格自平衡的多路查找树，由1986年图灵奖得主，美国理论计算机科学家 John Edward Hopcroft 在1970年发明，又称 3阶的B树 (注：B 为 Balance 平衡的意思)

它不是一棵二叉树，是一棵三叉树。具有以下特征：

1. 内部节点要么有1个数据元素和2个孩子，要么有2个数据元素和3个孩子，叶子节点没有孩子，但有1或2个数据元素。
2. 所有叶子节点到根节点的长度一致。这个特征保证了完全平衡，非常完美的平衡。
3. 每个节点的数据元素保持从小到大排序，两个数据元素之间的子树的所有值大小介于两个数据元素之间。

因为 2-3 树的第二个特征，它是一棵完美平衡的树，非常完美，除了叶子节点，其他的节点都没有空儿子，所以树的高度非常的小。

如图：

如果一个内部节点拥有一个数据元素、两个子节点，则此节点为2节点。如果一个内部节点拥有两个数据元素、三个子节点，则此节点为3节点。

可以说，所有平衡树的核心都在于插入和删除逻辑，我们主要分析这两个操作。

1.2. 2-3 树插入元素

在插入元素时，需要先找到插入的位置，使用二分查找从上自下查找树节点。

找到插入位置时，将元素插入该位置，然后进行调整，使得满足 2-3 树的特征。主要有三种情况：

1. 插入元素到一个2节点，直接插入即可，这样节点变成3节点。
2. 插入元素到一个3节点，该3节点的父亲是一个2节点，先将节点变成临时的4节点，然后向上分裂调整一次。
3. 插入元素到一个3节点，该3节点的父亲是一个3节点，先将节点变成临时的4节点，然后向上分裂调整，此时父亲节点变为临时4节点，继续向上分裂调整。

如图（来自维基百科）：

核心在于插入3节点后，该节点变为临时4节点，然后进行分裂恢复树的特征。最坏情况为插入节点后，每一次分裂后都导致上一层变为临时4节点，直到树根节点，这样需要不断向上分裂。

临时4节点的分裂，细分有六种情况，如图：

与其他二叉查找树由上而下生长不同，2-3 树是从下至上的生长。

2-3 树的实现将会放在 B树 章节，我们将会在此章节实现其二叉树形式的左倾红黑树结构。

1.3. 2-3 树删除元素

删除操作就复杂得多了，请耐心阅读理解。

2-3 树的特征注定它是一棵非常完美平衡的三叉树，其所有子树也都是完美平衡，所以 2-3 树的某节点的儿子，要么都是空儿子，要么都不是空儿子。比如 2-3 树的某个节点 A 有两个儿子 B 和 C，儿子 B 和 C 要么都没有孩子，要么孩子都是满的，不然 2-3 树所有叶子节点到根节点的长度一致这个特征就被破坏了。

基于上面的现实，我们来分析删除的不同情况，删除中间节点和叶子节点。

情况1：删除中间节点

删除的是非叶子节点，该节点一定是有两棵或者三棵子树的，那么从子树中找到其最小后继节点，该节点是叶子节点，用该节点替换被删除的非叶子节点，然后再删除这个叶子节点，进入情况2。

如何找到最小后继节点，当有两棵子树时，那么从右子树一直往左下方找，如果有三棵子树，被删除节点在左边，那么从中子树一直往左下方找，否则从右子树一直往左下方找。

情况2：删除叶子节点

删除的是叶子节点，这时如果叶子节点是3节点，那么直接变为2节点即可，不影响平衡。但是，如果叶子节点是2节点，那么删除后，其父节点将会缺失一个儿子，破坏了满孩子的 2-3 树特征，需要进行调整后才能删除。

针对情况2，删除一个2节点的叶子节点，会导致父节点缺失一个儿子，破坏了 2-3 树的特征，我们可以进行调整变换，主要有两种调整：

1. 重新分布：尝试从兄弟节点那里借值，然后重新调整节点。
2. 合并：如果兄弟借不到值，合并节点（与父亲的元素），再向上递归处理。

看图说话：

如果被删除的叶子节点有兄弟是3节点，那么从兄弟那里借一个值填补被删除的叶子节点，然后兄弟和父亲重新分布调整位置。下面是重新分布的具体例子：

可以看到，删除 100，从兄弟那里借来一个值 80，然后重新调整父亲，兄弟们的位置。

如果兄弟们都是2节点呢，那么就合并节点：将父亲和兄弟节点合并，如果父亲是2节点，那么父亲就留空了，否则父亲就从3节点变成2节点，下面是合并的两个具体例子：

可以看到，删除 80，而兄弟节点 60 和父亲节点 90 都是个2节点，所以父亲下来和兄弟合并，然后父亲变为空节点。

可以看到，删除 70，而兄弟节点都为2节点，父亲节点为3节点，那么父亲下来和其中一个兄弟合并，然后父亲从3节点变为2节点。

但是，如果合并后，父亲节点变空了，也就是说有中间节点留空要怎么办，那么可以继续递归处理，如图：

中间节点是空的，那么可以继续从兄弟那里借节点或者和父亲合并，直到根节点，如果到达了根节点呢，如图：

递归到了根节点后，如果存在空的根节点，我们可以直接把该空节点删除即可，这时树的高度减少一层。

2-3 树的实现将会放在 B树 章节，我们将会实现其二叉树形式的左倾红黑树结构。

二、 左倾红黑树

2.1. 左倾红黑树介绍

左倾红黑树可以由 2-3 树的二叉树形式来实现。

其定义为：

1. 根节点的链接是黑色的。
2. 红链接均为左链接。
3. 没有任何一个结点同时和两条红链接相连
4. 任意一个节点到达叶子节点的所有路径，经过的黑链接数量相同，也就是该树是完美黑色平衡的。比如，某一个节点，它可以到达5个叶子节点，那么这5条路径上的黑链接数量一样。

由于红链接都在左边，所以这种红黑树又称左倾红黑树。左倾红黑树与 2-3 树一一对应，只要将左链接画平，如图：

2.2. 节点旋转和颜色转换

首先，我们要定义树的结构 LLRBTree ，以及表示左倾红黑树的节点 LLRBTNode：

// 定义颜色
const (
    RED   = true
    BLACK = false
)
// 左倾红黑树
type LLRBTree struct {
    Root *LLRBTNode // 树根节点
}
// 左倾红黑树节点
type LLRBTNode struct {
    Value       int64     // 值
    Times       int64      // 值出现的次数
    Left        *LLRBTNode // 左子树
    Right       *LLRBTNode // 右子树
    Color       bool       // 父亲指向该节点的链接颜色
}
// 新建一棵空树
func NewLLRBTree() *LLRBTree {
    return &LLRBTree{}
}
// 节点的颜色
func IsRed(node *LLRBTNode) bool {
    if node == nil {
        return false
    }
    return node.Color == RED
}

在节点 LLRBTNode 中，我们存储的元素字段为 Value，由于可能有重复的元素插入，所以多了一个 Times 字段，表示该元素出现几次。

当然，红黑树中的红黑颜色使用 Color 定义，表示父亲指向该节点的链接颜色。为了方便，我们还构造了一个辅助函数 IsRed()。

在元素添加和实现的过程中，需要做调整操作，有两种旋转操作，对某节点的右链接进行左旋转，或者左链接进行右旋转。

如图是对节点 h 的右链接进行左旋转：

代码实现如下： 

// 左旋转
func RotateLeft(h *LLRBTNode) *LLRBTNode {
    if h == nil {
        return nil
    }
    // 看图理解
    x := h.Right
    h.Right = x.Left
    x.Left = h
    x.Color = h.Color
    h.Color = RED
    return x
}

如图是对节点 h 的左链接进行右旋转：

代码实现如下：

// 右旋转
func RotateRight(h *LLRBTNode) *LLRBTNode {
    if h == nil {
        return nil
    }
    // 看图理解
    x := h.Left
    h.Left = x.Right
    x.Right = h
    x.Color = h.Color
    h.Color = RED
    return x
}

由于左倾红黑树不允许一个节点有两个红链接，所以需要做颜色转换，如图：

代码如下：

1. // 颜色转换
2. func ColorChange(h *LLRBTNode) {
3. if h == nil {
4. return
5. }
6. h.Color = !h.Color
7. h.Left.Color = !h.Left.Color
8. h.Right.Color = !h.Right.Color
9. }

旋转和颜色转换作为局部调整，并不影响全局。

2.3. 添加元素实现

每次添加元素节点时，都将该节点 Color 字段，也就是父亲指向它的链接设置为 RED 红色。

接着判断其父亲是否有两个红链接（如连续的两个左红链接或者左右红色链接），或者有右红色链接，进行颜色变换或旋转操作。

主要有以下这几种情况。

插入元素到2节点，直接让节点变为3节点，不过当右插入时需要左旋使得红色链接在左边，如图：

 插入元素到3节点，需要做旋转和颜色转换操作，如图：

也就是说，在一个已经是红色左链接的节点，插入一个新节点的状态变化如下：

根据上述的演示图以及旋转，颜色转换等操作，添加元素的代码为：

// 左倾红黑树添加元素
func (tree *LLRBTree) Add(value int64) {
    // 跟节点开始添加元素，因为可能调整，所以需要将返回的节点赋值回根节点
    tree.Root = tree.Root.Add(value)
    // 根节点的链接永远都是黑色的
    tree.Root.Color = BLACK
}
// 往节点添加元素
func (node *LLRBTNode) Add(value int64) *LLRBTNode {
    // 插入的节点为空，将其链接颜色设置为红色，并返回
    if node == nil {
        return &LLRBTNode{
            Value: value,
            Color: RED,
        }
    }
    // 插入的元素重复
    if value == node.Value {
        node.Times = node.Times + 1
    } else if value > node.Value {
        // 插入的元素比节点值大，往右子树插入
        node.Right = node.Right.Add(value)
    } else {
        // 插入的元素比节点值小，往左子树插入
        node.Left = node.Left.Add(value)
    }
    // 辅助变量
    nowNode := node
    // 右链接为红色，那么进行左旋，确保树是左倾的
    // 这里做完操作后就可以结束了，因为插入操作，新插入的右红链接左旋后，nowNode节点不会出现连续两个红左链接，因为它只有一个左红链接
    if IsRed(nowNode.Right) && !IsRed(nowNode.Left) {
        nowNode = RotateLeft(nowNode)
    } else {
        // 连续两个左链接为红色，那么进行右旋
        if IsRed(nowNode.Left) && IsRed(nowNode.Left.Left) {
            nowNode = RotateRight(nowNode)
        }
        // 旋转后，可能左右链接都为红色，需要变色
        if IsRed(nowNode.Left) && IsRed(nowNode.Right) {
            ColorChange(nowNode)
        }
    }
    return nowNode
}

2.4. 添加元素算法分析

可参考论文： Left-leaning Red-Black Trees。

左倾红黑树的最坏树高度为 2log(n)，其中 n 为树的节点数量。为什么呢，我们先把左倾红黑树当作 2-3 树，也就是说最坏情况下沿着 2-3 树左边的节点都是3节点，其他节点都是2节点，这时树高近似 log(n)，再从 2-3 树转成左倾红黑树，当3节点不画平时，可以知道树高变成原来 2-3 树树高的两倍。虽然如此，构造一棵最坏的左倾红黑树很难。

AVL 树的最坏树高度为 1.44log(n)。由于左倾红黑树是近似平衡的二叉树，没有 AVL 树的严格平衡，树的高度会更高一点，因此查找操作效率比 AVL 树低，但时间复杂度只在于常数项的差别，去掉常数项，时间复杂度仍然是 log(n)。

我们的代码实现中，左倾红黑树的插入，需要逐层判断是否需要旋转和变色，复杂度为 log(n)，当旋转变色后导致上层存在连续的红左链接或者红色左右链接，那么需要继续旋转和变色，可能有多次这种调整操作，如图在箭头处添加新节点，出现了右红链接，要一直向上变色到根节点（实际上穿投到根节点的情况极少发生）：

我们可以优化代码，使得在某一层旋转变色后，如果其父层没有连续的左红链接或者不需要变色，那么可以直接退出，不需要逐层判断是否需要旋转和变色。

对于 AVL 树来说，插入最多旋转两次，但其需要逐层更新树高度，复杂度也是为 log(n)。

按照插入效率来说，很多教程都说左倾红黑树会比 AVL 树好一点，因为其不要求严格的平衡，会插入得更快点，但根据我们实际上的递归代码，两者都需要逐层向上判断是否需要调整，只不过 AVL 树多了更新树高度的操作，此操作影响了一点点效率，但我觉得两种树的插入效率都差不多。

在此，我们不再纠结两种平衡树哪种更好，因为代码实现中，两种平衡树都需要自底向上的递归操作，效率差别不大。。

2.5. 删除元素实现

删除操作就复杂得多了。对照一下 2-3 树。

1. 情况1：如果删除的是非叶子节点，找到其最小后驱节点，也就是在其右子树中一直向左找，找到的该叶子节点替换被删除的节点，然后删除该叶子节点，变成情况2。
2. 情况2：如果删除的是叶子节点，如果它是红节点，也就是父亲指向它的链接为红色，那么直接删除即可。否则，我们需要进行调整，使它变为红节点，再删除。

在这里，为了使得删除叶子节点时可以直接删除，叶子节点必须变为红节点。（在 2-3 树中，也就是2节点要变成3节点，我们知道要不和父亲合并再递归向上，要不向兄弟借值然后重新分布）

我们创造两种操作，如果删除的节点在左子树中，可能需要进行红色左移，如果删除的节点在右子树中，可能需要进行红色右移。

我们介绍红色左移的步骤：

要在树 h 的的左子树中删除元素，这时树 h 根节点是红节点，其儿子 b，d 节点都为黑色节点，且两个黑色节点都是2节点，都没有左红孩子，那么直接对 h 树根节点变色即可（相当于 2-3 树：把父亲的一个值拉下来合并），如图：

如果存在右儿子 d 是3节点，有左红孩子 e，那么需要先对 h 树根节点变色后，对右儿子 d 右旋，再对 h 树根节点左旋，最后再一次对 h 树根节点变色（相当于 2-3 树：向3节点兄弟借值，然后重新分布），如图：

红色左移可以总结为下图（被删除的节点在左子树，且进入的树根h一定为红节点）：

代码如下：

1. // 红色左移
2. // 节点 h 是红节点，其左儿子和左儿子的左儿子都为黑节点，左移后使得其左儿子或左儿子的左儿子有一个是红色节点
3. func MoveRedLeft(h *LLRBTNode) *LLRBTNode {
4. // 应该确保 isRed(h) && !isRed(h.left) && !isRed(h.left.left)
5. ColorChange(h)
7. // 右儿子有左红链接
8. if IsRed(h.Right.Left) {
9. // 对右儿子右旋
10. h.Right = RotateRight(h.Right)
11. // 再左旋
12. h = RotateLeft(h)
13. ColorChange(h)
14. }
16. return h
17. }

为什么要红色左移，是要保证调整后，子树根节点 h 的左儿子或左儿子的左儿子有一个是红色节点，这样从 h 的左子树递归删除元素才可以继续下去。

红色右移的步骤类似，如图（被删除的节点在右子树，且进入的树根h一定为红节点）：

代码如下：

1. // 红色右移
2. // 节点 h 是红节点，其右儿子和右儿子的左儿子都为黑节点，右移后使得其右儿子或右儿子的右儿子有一个是红色节点
3. func MoveRedRight(h *LLRBTNode) *LLRBTNode {
4. // 应该确保 isRed(h) && !isRed(h.right) && !isRed(h.right.left);
5. ColorChange(h)
7. // 左儿子有左红链接
8. if IsRed(h.Left.Left) {
9. // 右旋
10. h = RotateRight(h)
11. // 变色
12. ColorChange(h)
13. }
15. return h
16. }

为什么要红色右移，同样是为了保证树根节点 h 的右儿子或右儿子的右儿子有一个是红色节点，往右子树递归删除元素可以继续下去。

介绍完两种操作后，我们要明确一下到底是如何删除元素的。

我们知道 2-3 树的删除是从叶子节点开始，自底向上的向兄弟节点借值，或和父亲合并，然后一直递归到根节点。左倾红黑树参考了这种做法，但更巧妙，左倾红黑树要保证一路上每次递归进入删除操作的子树树根一定是一个3节点，所以需要适当的红色左移或右移（类似于 2-3 树借值和合并），这样一直递归到叶子节点，叶子节点也会是一个3节点，然后就可以直接删除叶子节点，最后再自底向上的恢复左倾红黑树的特征。

下面是左倾红黑树从 树h 删除元素的示例图，往 树h 左子树和右子树删除元素分别有四种情况，后两种情况需要使用到红色左移或右移，状态演变之后， 树h 才可以从左或右子树进入下一次递归：

可以对照着大图，继续阅读下面的左倾红黑树删除元素代码：

// 左倾红黑树删除元素
func (tree *LLRBTree) Delete(value int64) {
    // 当找不到值时直接返回
    if tree.Find(value) == nil {
        return
    }
    if !IsRed(tree.Root.Left) && !IsRed(tree.Root.Right) {
        // 左右子树都是黑节点，那么先将根节点变为红节点，方便后面的红色左移或右移
        tree.Root.Color = RED
    }
    tree.Root = tree.Root.Delete(value)
    // 最后，如果根节点非空，永远都要为黑节点，赋值黑色
    if tree.Root != nil {
        tree.Root.Color = BLACK
    }
}

首先 tree.Find(value) 找到可以删除的值时才能进行删除。

当根节点的左右子树都为黑节点时，那么先将根节点变为红节点，方便后面的红色左移或右移。

删除完节点：tree.Root = tree.Root.Delete(value) 后，需要将根节点染回黑色，因为左倾红黑树的特征之一是根节点永远都是黑色。

核心的从子树中删除元素代码如下：

// 对该节点所在的子树删除元素
func (node *LLRBTNode) Delete(value int64) *LLRBTNode {
    // 辅助变量
    nowNode := node
    // 删除的元素比子树根节点小，需要从左子树删除
    if value < nowNode.Value {
        // 因为从左子树删除，所以要判断是否需要红色左移
        if !IsRed(nowNode.Left) && !IsRed(nowNode.Left.Left) {
            // 左儿子和左儿子的左儿子都不是红色节点，那么没法递归下去，先红色左移
            nowNode = MoveRedLeft(nowNode)
        }
        // 现在可以从左子树中删除了
        nowNode.Left = nowNode.Left.Delete(value)
    } else {
        // 删除的元素等于或大于树根节点
        // 左节点为红色，那么需要右旋，方便后面可以红色右移
        if IsRed(nowNode.Left) {
            nowNode = RotateRight(nowNode)
        }
        // 值相等，且没有右孩子节点，那么该节点一定是要被删除的叶子节点，直接删除
        // 为什么呢，反证，它没有右儿子，但有左儿子，因为左倾红黑树的特征，那么左儿子一定是红色，但是前面的语句已经把红色左儿子右旋到右边，不应该出现右儿子为空。
        if value == nowNode.Value && nowNode.Right == nil {
            return nil
        }
        // 因为从右子树删除，所以要判断是否需要红色右移
        if !IsRed(nowNode.Right) && !IsRed(nowNode.Right.Left) {
            // 右儿子和右儿子的左儿子都不是红色节点，那么没法递归下去，先红色右移
            nowNode = MoveRedRight(nowNode)
        }
        // 删除的节点找到了，它是中间节点，需要用最小后驱节点来替换它，然后删除最小后驱节点
        if value == nowNode.Value {
            minNode := nowNode.Right.FindMinValue()
            nowNode.Value = minNode.Value
            nowNode.Times = minNode.Times
            // 删除其最小后驱节点
            nowNode.Right = nowNode.Right.DeleteMin()
        } else {
            // 删除的元素比子树根节点大，需要从右子树删除
            nowNode.Right = nowNode.Right.Delete(value)
        }
    }
    // 最后，删除叶子节点后，需要恢复左倾红黑树特征
    return nowNode.FixUp()
}

这段核心代码十分复杂，会用到红色左移和右移，当删除的元素小于根节点时，我们明白要在左子树中删除，如：

1. // 删除的元素比子树根节点小，需要从左子树删除
2. if value < nowNode.Value {
3. // 因为从左子树删除，所以要判断是否需要红色左移
4. if !IsRed(nowNode.Left) && !IsRed(nowNode.Left.Left) {
5. // 左儿子和左儿子的左儿子都不是红色节点，那么没法递归下去，先红色左移
6. nowNode = MoveRedLeft(nowNode)
7. }
9. // 现在可以从左子树中删除了
10. nowNode.Left = nowNode.Left.Delete(value)
11. }

递归删除左子树前：nowNode.Left = nowNode.Left.Delete(value)，要确保删除的左子树根节点是红色节点，或左子树根节点的左儿子是红色节点，才能够继续递归下去，所以使用了 !IsRed(nowNode.Left) && !IsRed(nowNode.Left.Left) 来判断是否需要红色左移。

如果删除的值不小于根节点，那么进入以下逻辑（可仔细阅读注释）：

        // 删除的元素等于或大于树根节点
        // 左节点为红色，那么需要右旋，方便后面可以红色右移
        if IsRed(nowNode.Left) {
            nowNode = RotateRight(nowNode)
        }
        // 值相等，且没有右孩子节点，那么该节点一定是要被删除的叶子节点，直接删除
        // 为什么呢，反证，它没有右儿子，但有左儿子，因为左倾红黑树的特征，那么左儿子一定是红色，但是前面的语句已经把红色左儿子右旋到右边，不应该出现右儿子为空。
        if value == nowNode.Value && nowNode.Right == nil {
            return nil
        }
        // 因为从右子树删除，所以要判断是否需要红色右移
        if !IsRed(nowNode.Right) && !IsRed(nowNode.Right.Left) {
            // 右儿子和右儿子的左儿子都不是红色节点，那么没法递归下去，先红色右移
            nowNode = MoveRedRight(nowNode)
        }
        // 删除的节点找到了，它是中间节点，需要用最小后驱节点来替换它，然后删除最小后驱节点
        if value == nowNode.Value {
            minNode := nowNode.Right.FindMinValue()
            nowNode.Value = minNode.Value
            nowNode.Times = minNode.Times
            // 删除其最小后驱节点
            nowNode.Right = nowNode.Right.DeleteMin()
        } else {
            // 删除的元素比子树根节点大，需要从右子树删除
            nowNode.Right = nowNode.Right.Delete(value)
        }

首先，需要先判断该节点的左子树根节点是否为红色节点 IsRed(nowNode.Left)，如果是的话需要右旋：nowNode = RotateRight(nowNode)，将红节点右旋是为了后面可以递归进入右子树。

然后，判断删除的值是否等于当前根节点的值，且其没有右节点：value == nowNode.Value && nowNode.Right == nil，如果是，那么该节点就是要被删除的叶子节点，直接删除即可。

接着，判断是否需要红色右移：!IsRed(nowNode.Right) && !IsRed(nowNode.Right.Left)，如果该节点右儿子和右儿子的左儿子都不是红色节点，那么没法递归进入右子树，需要红色右移，必须确保其右子树或右子树的左儿子有一个是红色节点。

再接着，需要判断是否找到了要删除的节点：value == nowNode.Value，找到时表示要删除的节点处于内部节点，需要用最小后驱节点来替换它，然后删除最小后驱节点。

找到最小后驱节点：minNode := nowNode.Right.FindMinValue() 后，将最小后驱节点与要删除的内部节点替换，然后删除最小后驱节点：nowNode.Right = nowNode.Right.DeleteMin()，删除最小节点代码如下：

// 对该节点所在的子树删除最小元素
func (node *LLRBTNode) DeleteMin() *LLRBTNode {
    // 辅助变量
    nowNode := node
    // 没有左子树，那么删除它自己
    if nowNode.Left == nil {
        return nil
    }
    // 判断是否需要红色左移，因为最小元素在左子树中
    if !IsRed(nowNode.Left) && !IsRed(nowNode.Left.Left) {
        nowNode = MoveRedLeft(nowNode)
    }
    // 递归从左子树删除
    nowNode.Left = nowNode.Left.DeleteMin()
    // 修复左倾红黑树特征
    return nowNode.FixUp()
}

因为最小节点在最左的叶子节点，所以只需要适当的红色左移，然后一直左子树递归即可。递归完后需要修复左倾红黑树特征 nowNode.FixUp()，代码如下：

// 修复左倾红黑树特征
func (node *LLRBTNode) FixUp() *LLRBTNode {
    // 辅助变量
    nowNode := node
    // 红链接在右边，左旋恢复，让红链接只出现在左边
    if IsRed(nowNode.Right) {
        nowNode = RotateLeft(nowNode)
    }
    // 连续两个左链接为红色，那么进行右旋
    if IsRed(nowNode.Left) && IsRed(nowNode.Left.Left) {
        nowNode = RotateRight(nowNode)
    }
    // 旋转后，可能左右链接都为红色，需要变色
    if IsRed(nowNode.Left) && IsRed(nowNode.Right) {
        ColorChange(nowNode)
    }
    return nowNode
}

如果不是删除内部节点，依然是从右子树继续递归：

1. // 删除的元素比子树根节点大，需要从右子树删除
2. nowNode.Right = nowNode.Right.Delete(value)

当然，递归完成后还要进行一次 FixUp()，恢复左倾红黑树的特征。

删除操作很难理解，可以多多思考，红色左移和右移不断地递归都是为了确保删除叶子节点时，其是一个3节点。

PS：如果不理解自顶向下的红色左移和右移递归思路，可以更换另外一种方法，使用原先 2-3树 删除元素操作步骤来实现，一开始从叶子节点删除，然后自底向上的向兄弟借值或与父亲合并，这是更容易理解的，我们不在这里进行展示了，可以借鉴普通红黑树章节的删除实现（它使用了自底向上的调整）。

完整代码见最下面。

2.6. 删除元素算法分析

左倾红黑树删除元素需要自顶向下的递归，可能不断地红色左移和右移，也就是有很多的旋转，当删除叶子节点后，还需要逐层恢复左倾红黑树的特征。时间复杂度仍然是和树高有关：log(n)。

2.7. 查找元素等实现

查找最小值，最大值，或者某个值，代码如下：

// 找出最小值的节点
func (tree *LLRBTree) FindMinValue() *LLRBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMinValue()
}
func (node *LLRBTNode) FindMinValue() *LLRBTNode {
    // 左子树为空，表面已经是最左的节点了，该值就是最小值
    if node.Left == nil {
        return node
    }
    // 一直左子树递归
    return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *LLRBTree) FindMaxValue() *LLRBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMaxValue()
}
func (node *LLRBTNode) FindMaxValue() *LLRBTNode {
    // 右子树为空，表面已经是最右的节点了，该值就是最大值
    if node.Right == nil {
        return node
    }
    // 一直右子树递归
    return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *LLRBTree) Find(value int64) *LLRBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.Find(value)
}
func (node *LLRBTNode) Find(value int64) *LLRBTNode {
    if value == node.Value {
        // 如果该节点刚刚等于该值，那么返回该节点
        return node
    } else if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        if node.Left == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Left.Find(value)
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        if node.Right == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Right.Find(value)
    }
}
// 中序遍历
func (tree *LLRBTree) MidOrder() {
    tree.Root.MidOrder()
}
func (node *LLRBTNode) MidOrder() {
    if node == nil {
        return
    }
    // 先打印左子树
    node.Left.MidOrder()
    // 按照次数打印根节点
    for i := 0; i <= int(node.Times); i++ {
        fmt.Println(node.Value)
    }
    // 打印右子树
    node.Right.MidOrder()
}

查找操作逻辑与通用的二叉查找树一样，并无区别。

2.8. 验证是否是一棵左倾红黑树

如何确保我们的代码实现的就是一棵左倾红黑树呢，可以进行验证：

// 验证是不是棵左倾红黑树
func (tree *LLRBTree) IsLLRBTree() bool {
    if tree == nil || tree.Root == nil {
        return true
    }
    // 判断树是否是一棵二分查找树
    if !tree.Root.IsBST() {
        return false
    }
    // 判断树是否遵循2-3树，也就是红链接只能在左边，不能连续有两个红链接
    if !tree.Root.Is23() {
        return false
    }
    // 判断树是否平衡，也就是任意一个节点到叶子节点，经过的黑色链接数量相同
    // 先计算根节点到最左边叶子节点的黑链接数量
    blackNum := 0
    x := tree.Root
    for x != nil {
        if !IsRed(x) { // 是黑色链接
            blackNum = blackNum + 1
        }
        x = x.Left
    }
    if !tree.Root.IsBalanced(blackNum) {
        return false
    }
    return true
}
// 节点所在的子树是否是一棵二分查找树
func (node *LLRBTNode) IsBST() bool {
    if node == nil {
        return true
    }
    // 左子树非空，那么根节点必须大于左儿子节点
    if node.Left != nil {
        if node.Value > node.Left.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 右子树非空，那么根节点必须小于右儿子节点
    if node.Right != nil {
        if node.Value < node.Right.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 左子树也要判断是否是平衡查找树
    if !node.Left.IsBST() {
        return false
    }
    // 右子树也要判断是否是平衡查找树
    if !node.Right.IsBST() {
        return false
    }
    return true
}
// 节点所在的子树是否遵循2-3树
func (node *LLRBTNode) Is23() bool {
    if node == nil {
        return true
    }
    // 不允许右倾红链接
    if IsRed(node.Right) {
        fmt.Printf("father:%#v,rchild:%#v\n", node, node.Right)
        return false
    }
    // 不允许连续两个左红链接
    if IsRed(node) && IsRed(node.Left) {
        fmt.Printf("father:%#v,lchild:%#v\n", node, node.Left)
        return false
    }
    // 左子树也要判断是否遵循2-3树
    if !node.Left.Is23() {
        return false
    }
    // 右子树也要判断是否是遵循2-3树
    if !node.Right.Is23() {
        return false
    }
    return true
}
// 节点所在的子树是否平衡，是否有 blackNum 个黑链接
func (node *LLRBTNode) IsBalanced(blackNum int) bool {
    if node == nil {
        return blackNum == 0
    }
    if !IsRed(node) {
        blackNum = blackNum - 1
    }
    if !node.Left.IsBalanced(blackNum) {
        fmt.Println("node.Left to leaf black link is not ", blackNum)
        return false
    }
    if !node.Right.IsBalanced(blackNum) {
        fmt.Println("node.Right to leaf black link is not ", blackNum)
        return false
    }
    return true
}

运行请看完整代码。

2.9. 完整程序

package main
import "fmt"
// 左倾红黑树实现
// Left-leaning red-black tree
// 定义颜色
const (
    RED   = true
    BLACK = false
)
// 左倾红黑树
type LLRBTree struct {
    Root *LLRBTNode // 树根节点
}
// 新建一棵空树
func NewLLRBTree() *LLRBTree {
    return &LLRBTree{}
}
// 左倾红黑树节点
type LLRBTNode struct {
    Value int64      // 值
    Times int64      // 值出现的次数
    Left  *LLRBTNode // 左子树
    Right *LLRBTNode // 右子树
    Color bool       // 父亲指向该节点的链接颜色
}
// 节点的颜色
func IsRed(node *LLRBTNode) bool {
    if node == nil {
        return false
    }
    return node.Color == RED
}
// 左旋转
func RotateLeft(h *LLRBTNode) *LLRBTNode {
    if h == nil {
        return nil
    }
    // 看图理解
    x := h.Right
    h.Right = x.Left
    x.Left = h
    x.Color = h.Color
    h.Color = RED
    return x
}
// 右旋转
func RotateRight(h *LLRBTNode) *LLRBTNode {
    if h == nil {
        return nil
    }
    // 看图理解
    x := h.Left
    h.Left = x.Right
    x.Right = h
    x.Color = h.Color
    h.Color = RED
    return x
}
// 红色左移
// 节点 h 是红节点，其左儿子和左儿子的左儿子都为黑节点，左移后使得其左儿子或左儿子的左儿子有一个是红色节点
func MoveRedLeft(h *LLRBTNode) *LLRBTNode {
    // 应该确保 isRed(h) && !isRed(h.left) && !isRed(h.left.left)
    ColorChange(h)
    // 右儿子有左红链接
    if IsRed(h.Right.Left) {
        // 对右儿子右旋
        h.Right = RotateRight(h.Right)
        // 再左旋
        h = RotateLeft(h)
        ColorChange(h)
    }
    return h
}
// 红色右移
// 节点 h 是红节点，其右儿子和右儿子的左儿子都为黑节点，右移后使得其右儿子或右儿子的右儿子有一个是红色节点
func MoveRedRight(h *LLRBTNode) *LLRBTNode {
    // 应该确保 isRed(h) && !isRed(h.right) && !isRed(h.right.left);
    ColorChange(h)
    // 左儿子有左红链接
    if IsRed(h.Left.Left) {
        // 右旋
        h = RotateRight(h)
        // 变色
        ColorChange(h)
    }
    return h
}
// 颜色变换
func ColorChange(h *LLRBTNode) {
    if h == nil {
        return
    }
    h.Color = !h.Color
    h.Left.Color = !h.Left.Color
    h.Right.Color = !h.Right.Color
}
// 左倾红黑树添加元素
func (tree *LLRBTree) Add(value int64) {
    // 跟节点开始添加元素，因为可能调整，所以需要将返回的节点赋值回根节点
    tree.Root = tree.Root.Add(value)
    // 根节点的链接永远都是黑色的
    tree.Root.Color = BLACK
}
// 往节点添加元素
func (node *LLRBTNode) Add(value int64) *LLRBTNode {
    // 插入的节点为空，将其链接颜色设置为红色，并返回
    if node == nil {
        return &LLRBTNode{
            Value: value,
            Color: RED,
        }
    }
    // 插入的元素重复
    if value == node.Value {
        node.Times = node.Times + 1
    } else if value > node.Value {
        // 插入的元素比节点值大，往右子树插入
        node.Right = node.Right.Add(value)
    } else {
        // 插入的元素比节点值小，往左子树插入
        node.Left = node.Left.Add(value)
    }
    // 辅助变量
    nowNode := node
    // 右链接为红色，那么进行左旋，确保树是左倾的
    // 这里做完操作后就可以结束了，因为插入操作，新插入的右红链接左旋后，nowNode节点不会出现连续两个红左链接，因为它只有一个左红链接
    if IsRed(nowNode.Right) && !IsRed(nowNode.Left) {
        nowNode = RotateLeft(nowNode)
    } else {
        // 连续两个左链接为红色，那么进行右旋
        if IsRed(nowNode.Left) && IsRed(nowNode.Left.Left) {
            nowNode = RotateRight(nowNode)
        }
        // 旋转后，可能左右链接都为红色，需要变色
        if IsRed(nowNode.Left) && IsRed(nowNode.Right) {
            ColorChange(nowNode)
        }
    }
    return nowNode
}
// 找出最小值的节点
func (tree *LLRBTree) FindMinValue() *LLRBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMinValue()
}
func (node *LLRBTNode) FindMinValue() *LLRBTNode {
    // 左子树为空，表面已经是最左的节点了，该值就是最小值
    if node.Left == nil {
        return node
    }
    // 一直左子树递归
    return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *LLRBTree) FindMaxValue() *LLRBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMaxValue()
}
func (node *LLRBTNode) FindMaxValue() *LLRBTNode {
    // 右子树为空，表面已经是最右的节点了，该值就是最大值
    if node.Right == nil {
        return node
    }
    // 一直右子树递归
    return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *LLRBTree) Find(value int64) *LLRBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.Find(value)
}
func (node *LLRBTNode) Find(value int64) *LLRBTNode {
    if value == node.Value {
        // 如果该节点刚刚等于该值，那么返回该节点
        return node
    } else if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        if node.Left == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Left.Find(value)
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        if node.Right == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Right.Find(value)
    }
}
// 中序遍历
func (tree *LLRBTree) MidOrder() {
    tree.Root.MidOrder()
}
func (node *LLRBTNode) MidOrder() {
    if node == nil {
        return
    }
    // 先打印左子树
    node.Left.MidOrder()
    // 按照次数打印根节点
    for i := 0; i <= int(node.Times); i++ {
        fmt.Println(node.Value)
    }
    // 打印右子树
    node.Right.MidOrder()
}
// 修复左倾红黑树特征
func (node *LLRBTNode) FixUp() *LLRBTNode {
    // 辅助变量
    nowNode := node
    // 红链接在右边，左旋恢复，让红链接只出现在左边
    if IsRed(nowNode.Right) {
        nowNode = RotateLeft(nowNode)
    }
    // 连续两个左链接为红色，那么进行右旋
    if IsRed(nowNode.Left) && IsRed(nowNode.Left.Left) {
        nowNode = RotateRight(nowNode)
    }
    // 旋转后，可能左右链接都为红色，需要变色
    if IsRed(nowNode.Left) && IsRed(nowNode.Right) {
        ColorChange(nowNode)
    }
    return nowNode
}
// 对该节点所在的子树删除最小元素
func (node *LLRBTNode) DeleteMin() *LLRBTNode {
    // 辅助变量
    nowNode := node
    // 没有左子树，那么删除它自己
    if nowNode.Left == nil {
        return nil
    }
    // 判断是否需要红色左移，因为最小元素在左子树中
    if !IsRed(nowNode.Left) && !IsRed(nowNode.Left.Left) {
        nowNode = MoveRedLeft(nowNode)
    }
    // 递归从左子树删除
    nowNode.Left = nowNode.Left.DeleteMin()
    // 修复左倾红黑树特征
    return nowNode.FixUp()
}
// 左倾红黑树删除元素
func (tree *LLRBTree) Delete(value int64) {
    // 当找不到值时直接返回
    if tree.Find(value) == nil {
        return
    }
    if !IsRed(tree.Root.Left) && !IsRed(tree.Root.Right) {
        // 左右子树都是黑节点，那么先将根节点变为红节点，方便后面的红色左移或右移
        tree.Root.Color = RED
    }
    tree.Root = tree.Root.Delete(value)
    // 最后，如果根节点非空，永远都要为黑节点，赋值黑色
    if tree.Root != nil {
        tree.Root.Color = BLACK
    }
}
// 对该节点所在的子树删除元素
func (node *LLRBTNode) Delete(value int64) *LLRBTNode {
    // 辅助变量
    nowNode := node
    // 删除的元素比子树根节点小，需要从左子树删除
    if value < nowNode.Value {
        // 因为从左子树删除，所以要判断是否需要红色左移
        if !IsRed(nowNode.Left) && !IsRed(nowNode.Left.Left) {
            // 左儿子和左儿子的左儿子都不是红色节点，那么没法递归下去，先红色左移
            nowNode = MoveRedLeft(nowNode)
        }
        // 现在可以从左子树中删除了
        nowNode.Left = nowNode.Left.Delete(value)
    } else {
        // 删除的元素等于或大于树根节点
        // 左节点为红色，那么需要右旋，方便后面可以红色右移
        if IsRed(nowNode.Left) {
            nowNode = RotateRight(nowNode)
        }
        // 值相等，且没有右孩子节点，那么该节点一定是要被删除的叶子节点，直接删除
        // 为什么呢，反证，它没有右儿子，但有左儿子，因为左倾红黑树的特征，那么左儿子一定是红色，但是前面的语句已经把红色左儿子右旋到右边，不应该出现右儿子为空。
        if value == nowNode.Value && nowNode.Right == nil {
            return nil
        }
        // 因为从右子树删除，所以要判断是否需要红色右移
        if !IsRed(nowNode.Right) && !IsRed(nowNode.Right.Left) {
            // 右儿子和右儿子的左儿子都不是红色节点，那么没法递归下去，先红色右移
            nowNode = MoveRedRight(nowNode)
        }
        // 删除的节点找到了，它是中间节点，需要用最小后驱节点来替换它，然后删除最小后驱节点
        if value == nowNode.Value {
            minNode := nowNode.Right.FindMinValue()
            nowNode.Value = minNode.Value
            nowNode.Times = minNode.Times
            // 删除其最小后驱节点
            nowNode.Right = nowNode.Right.DeleteMin()
        } else {
            // 删除的元素比子树根节点大，需要从右子树删除
            nowNode.Right = nowNode.Right.Delete(value)
        }
    }
    // 最后，删除叶子节点后，需要恢复左倾红黑树特征
    return nowNode.FixUp()
}
// 验证是不是棵左倾红黑树
func (tree *LLRBTree) IsLLRBTree() bool {
    if tree == nil || tree.Root == nil {
        return true
    }
    // 判断树是否是一棵二分查找树
    if !tree.Root.IsBST() {
        return false
    }
    // 判断树是否遵循2-3树，也就是红链接只能在左边，不能连续有两个红链接
    if !tree.Root.Is23() {
        return false
    }
    // 判断树是否平衡，也就是任意一个节点到叶子节点，经过的黑色链接数量相同
    // 先计算根节点到最左边叶子节点的黑链接数量
    blackNum := 0
    x := tree.Root
    for x != nil {
        if !IsRed(x) { // 是黑色链接
            blackNum = blackNum + 1
        }
        x = x.Left
    }
    if !tree.Root.IsBalanced(blackNum) {
        return false
    }
    return true
}
// 节点所在的子树是否是一棵二分查找树
func (node *LLRBTNode) IsBST() bool {
    if node == nil {
        return true
    }
    // 左子树非空，那么根节点必须大于左儿子节点
    if node.Left != nil {
        if node.Value > node.Left.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 右子树非空，那么根节点必须小于右儿子节点
    if node.Right != nil {
        if node.Value < node.Right.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 左子树也要判断是否是平衡查找树
    if !node.Left.IsBST() {
        return false
    }
    // 右子树也要判断是否是平衡查找树
    if !node.Right.IsBST() {
        return false
    }
    return true
}
// 节点所在的子树是否遵循2-3树
func (node *LLRBTNode) Is23() bool {
    if node == nil {
        return true
    }
    // 不允许右倾红链接
    if IsRed(node.Right) {
        fmt.Printf("father:%#v,rchild:%#v\n", node, node.Right)
        return false
    }
    // 不允许连续两个左红链接
    if IsRed(node) && IsRed(node.Left) {
        fmt.Printf("father:%#v,lchild:%#v\n", node, node.Left)
        return false
    }
    // 左子树也要判断是否遵循2-3树
    if !node.Left.Is23() {
        return false
    }
    // 右子树也要判断是否是遵循2-3树
    if !node.Right.Is23() {
        return false
    }
    return true
}
// 节点所在的子树是否平衡，是否有 blackNum 个黑链接
func (node *LLRBTNode) IsBalanced(blackNum int) bool {
    if node == nil {
        return blackNum == 0
    }
    if !IsRed(node) {
        blackNum = blackNum - 1
    }
    if !node.Left.IsBalanced(blackNum) {
        fmt.Println("node.Left to leaf black link is not ", blackNum)
        return false
    }
    if !node.Right.IsBalanced(blackNum) {
        fmt.Println("node.Right to leaf black link is not ", blackNum)
        return false
    }
    return true
}
func main() {
    tree := NewLLRBTree()
    values := []int64{2, 3, 7, 10, 10, 10, 10, 23, 9, 102, 109, 111, 112, 113}
    for _, v := range values {
        tree.Add(v)
    }
    // 找到最大值或最小值的节点
    fmt.Println("find min value:", tree.FindMinValue())
    fmt.Println("find max value:", tree.FindMaxValue())
    // 查找不存在的99
    node := tree.Find(99)
    if node != nil {
        fmt.Println("find it 99!")
    } else {
        fmt.Println("not find it 99!")
    }
    // 查找存在的9
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    tree.MidOrder()
    // 删除存在的9后，再查找9
    tree.Delete(9)
    tree.Delete(10)
    tree.Delete(2)
    tree.Delete(3)
    tree.Add(4)
    tree.Add(3)
    tree.Add(10)
    tree.Delete(111)
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    if tree.IsLLRBTree() {
        fmt.Println("is a llrb tree")
    } else {
        fmt.Println("is not llrb tree")
    }
}

PS：我们的程序是递归程序，如果改写为非递归形式，效率和性能会更好，在此就不实现了，理解左倾红黑树添加和删除的总体思路即可。

三、应用场景

红黑树可以用来作为字典 Map 的基础数据结构，可以存储键值对，然后通过一个键，可以快速找到键对应的值，相比哈希表查找，不需要占用额外的空间。我们以上的代码实现只有 value，没有 key:value，可以简单改造实现字典。

Java 语言基础类库中的 HashMap，TreeSet，TreeMap 都有使用到，C++ 语言的 STL 标准模板库中，map 和 set 类也有使用到。很多中间件也有使用到，比如 Nginx，但 Golang 语言标准库并没有它。

最后，上述应用场景使用的红黑树都是普通红黑树，并不是本文所介绍的左倾红黑树。

左倾红黑树作为红黑树的一个变种，只是被设计为更容易理解而已，变种只能是变种，工程上使用得更多的还是普通红黑树，所以我们仍然需要学习普通的红黑树，请看下一章节。

2-3-4树和普通红黑树

某些教程不区分普通红黑树和左倾红黑树的区别，直接将左倾红黑树拿来教学，并且称其为红黑树，因为左倾红黑树与普通的红黑树相比，实现起来较为简单，容易教学。在这里，我们区分开左倾红黑树和普通红黑树。

红黑树是一种近似平衡的二叉查找树，从 2-3 树或 2-3-4 树衍生而来。通过对二叉树节点进行染色，染色为红或黑节点，来模仿 2-3 树或 2-3-4 树的3节点和4节点，从而让树的高度减小。2-3-4 树对照实现的红黑树是普通的红黑树，而 2-3 树对照实现的红黑树是一种变种，称为左倾红黑树，其更容易实现。

使用平衡树数据结构，可以提高查找元素的速度，我们在本章介绍 2-3-4 树，再用二叉树形式来实现 2-3-4 树，也就是普通的红黑树。

一、2-3-4 树

1.1. 2-3-4 树介绍

2-3-4 树是一棵严格自平衡的多路查找树，又称 4阶的B树 (注：B 为 Balance 平衡的意思)

它不是一棵二叉树，是一棵四叉树。具有以下特征：

1. 内部节点要么有1个数据元素和2个孩子，要么有2个数据元素和3个孩子，要么有3个数据元素和4个孩子，叶子节点没有孩子，但有1，2或3个数据元素。
2. 所有叶子节点到根节点的长度一致。这个特征保证了完全平衡，非常完美的平衡。
3. 每个节点的数据元素保持从小到大排序，两个数据元素之间的子树的所有值大小介于两个数据元素之间。

因为 2-3-4 树的第二个特征，它是一棵完美平衡的树，非常完美，除了叶子节点，其他的节点都没有空儿子，所以树的高度非常的小。

如图：

如果一个内部节点拥有一个数据元素、两个子节点，则此节点为2节点。如果一个内部节点拥有两个数据元素、三个子节点，则此节点为3节点。如果一个内部节点拥有三个数据元素、四个子节点，则此节点为4节点。

可以说，所有平衡树的核心都在于插入和删除逻辑，我们主要分析这两个操作。

1.2. 2-3-4 树插入元素

在插入元素时，需要先找到插入的位置，使用二分查找从上自下查找树节点。

找到插入位置时，将元素插入该位置，然后进行调整，使得满足 2-3-4 树的特征。主要有三种情况：

1. 插入元素到一个2节点或3节点，直接插入即可，这样节点变成3节点或4节点。
2. 插入元素到一个4节点，该4节点的父亲不是一个4节点，将4节点的中间元素提到父节点，原4节点变成两个2节点，再将元素插入到其中一个2节点。
3. 插入元素到一个4节点，该4节点的父亲是一个4节点，也是将4节点的中间元素提到父节点，原4节点变成两个2节点，再将元素插入到其中一个2节点。当中间元素提到父节点时，父节点也是4节点，可以递归向上操作。

核心在于往4节点插入元素时，需要将4节点中间元素提升，4节点变为两个2节点后，再插入元素，如图：

下面演示插入元素到一个4节点：

与其他二叉查找树由上而下生长不同，2-3-4 树是从下至上的生长。

2-3-4 树因为节点元素数量的增加，情况变得更复杂，下面是插入元素到一个4节点，而4节点的父节点是3节点的三种情况：

其他情况可以参考 2-3树和左倾红黑树 一章，非常相似，在此不再赘述。

1.3. 2-3-4 树删除元素

删除操作就复杂得多了，请耐心阅读理解，和 2-3 树删除元素类似。

2-3-4 树的特征注定它是一棵非常完美平衡的四叉树，其所有子树也都是完美平衡，所以 2-3-4 树的某节点的儿子，要么都是空儿子，要么都不是空儿子。比如 2-3-4 树的某个节点 A 有两个儿子 B 和 C，儿子 B 和 C 要么都没有孩子，要么孩子都是满的，不然 2-3-4 树所有叶子节点到根节点的长度一致这个特征就被破坏了。

基于上面的现实，我们来分析删除的不同情况，删除中间节点和叶子节点。

情况1：删除中间节点

删除的是非叶子节点，该节点一定是有两棵，三棵或者四棵子树的，那么从子树中找到其最小后继节点，该节点是叶子节点，用该节点替换被删除的非叶子节点，然后再删除这个叶子节点，进入情况2。

如何找到最小后继节点，当有两棵子树时，那么从右子树一直往左下方找，如果有三棵子树，被删除节点在左边，那么从中子树一直往左下方找，否则从右子树一直往左下方找。如果有四棵子树，那么往被删除节点右边的子树，一直往左下方找。

情况2：删除叶子节点

删除的是叶子节点，这时叶子节点如果是4节点，直接变为3节点，如果是3节点，那么直接变为2节点即可，不影响平衡。但是，如果叶子节点是2节点，那么删除后，其父节点将会缺失一个儿子，破坏了满孩子的 2-3-4 树特征，需要进行调整后才能删除。

针对情况2，删除一个2节点的叶子节点，会导致父节点缺失一个儿子，破坏了 2-3-4 树的特征，我们可以进行调整变换，主要有两种调整：

1. 重新分布：尝试从兄弟节点那里借值，然后重新调整节点。
2. 合并：如果兄弟借不到值，合并节点（与父亲的元素）。

如果被删除的叶子节点有兄弟是3节点或4节点，可以向最近的兄弟借值，然后重新分布，这样叶子节点就不再是2节点了，删除元素后也不会破坏平衡。如图：

与兄弟借值，兄弟必须有多余的元素可以借，借的过程中需要和父节点元素重新分布位置，确保符合元素大小排序的正确。

如果被删除的叶子节点，兄弟都是2节点，而父亲是3节点或4节点，那么将父亲的一个元素拉下来进行合并（当父节点是3节点时，父亲元素与被删除节点合并成3节点，当父节点是4节点时，被删除节点和其最近的兄弟，以及父亲的一个元素合并成一个4节点），父亲变为2节点或3节点，这时叶子节点就不再是2节点了，删除元素后也不会破坏平衡。如图：

有一种最特殊的情况，也就是被删除的叶子节点，兄弟都是2节点，父亲也是2节点，这种情况没法向兄弟借，也没法和父亲合并，与父亲合并后父亲就变空了。幸运的是，这种特殊情况只会发生在根节点是其父节点的情况，如图： 

因为 2-3-4 树的性质，除了根节点，其他节点不可能出现其本身和儿子都是2节点。

2-3-4 树的实现将会放在 B树 章节，我们将会实现其二叉树形式的普通红黑树结构。

二、 普通红黑树

2.1. 普通红黑树介绍

普通红黑树可以由 2-3-4 树的二叉树形式来实现。

其定义为：

1. 根节点的链接是黑色的。
2. 每个红色节点都必须有两个黑色子节点。
3. 任意一个节点到达叶子节点的所有路径，经过的黑链接数量相同，也就是该树是完美黑色平衡的。比如，某一个节点，它可以到达5个叶子节点，那么这5条路径上的黑链接数量一样。

普通红黑树与其变种：左倾红黑树的区别是，它允许右倾的红色节点，不再限制左倾，但仍然不能有连续的两个左倾红色链接。

每一棵 2-3-4 树可以对应多棵普通红黑树，如图：

区别：2-3 树与左倾红黑树则是一一对应，而 2-3-4 树可以对应多棵普通红黑树，是因为它允许了红链接右倾。

2.2. 结构定义和节点旋转

首先，我们要定义树的结构 RBTree ，以及表示普通红黑树的节点 RBTNode：

// 定义颜色
const (
    RED   = true
    BLACK = false
)
// 普通红黑树
type RBTree struct {
    Root *RBTNode // 树根节点
}
// 新建一棵空树
func NewRBTree() *RBTree {
    return &RBTree{}
}
// 普通红黑树节点
type RBTNode struct {
    Value  int64    // 值
    Times  int64    // 值出现的次数
    Left   *RBTNode // 左子树
    Right  *RBTNode // 右子树
    Parent *RBTNode // 父节点
    Color  bool     // 父亲指向该节点的链接颜色
}
// 节点的颜色
func IsRed(node *RBTNode) bool {
    if node == nil {
        return false
    }
    return node.Color == RED
}
// 返回节点的父亲节点
func ParentOf(node *RBTNode) *RBTNode {
    if node == nil {
        return nil
    }
    return node.Parent
}
// 返回节点的左子节点
func LeftOf(node *RBTNode) *RBTNode {
    if node == nil {
        return nil
    }
    return node.Left
}
// 返回节点的右子节点
func RightOf(node *RBTNode) *RBTNode {
    if node == nil {
        return nil
    }
    return node.Right
}
// 设置节点颜色
func SetColor(node *RBTNode, color bool) {
    if node != nil {
        node.Color = color
    }
}

在节点 RBTNode 中，我们存储的元素字段为 Value，由于可能有重复的元素插入，所以多了一个 Times 字段，表示该元素出现几次。

当然，红黑树中的红黑颜色使用 Color 定义，表示父亲指向该节点的链接颜色。我们还多创建了几个辅助函数。

在元素添加和实现的过程中，需要做调整操作，有两种旋转操作，对某节点的右链接进行左旋转，如图：

代码如下：

// 对某节点左旋转
func (tree *RBTree) RotateLeft(h *RBTNode) {
    if h != nil {
        // 看图理解
        x := h.Right
        h.Right = x.Left
        if x.Left != nil {
            x.Left.Parent = h
        }
        x.Parent = h.Parent
        if h.Parent == nil {
            tree.Root = x
        } else if h.Parent.Left == h {
            h.Parent.Left = x
        } else {
            h.Parent.Right = x
        }
        x.Left = h
        h.Parent = x
    }
}

或者左链接进行右旋转，如图：

代码如下：

// 对某节点右旋转
func (tree *RBTree) RotateRight(h *RBTNode) {
    if h != nil {
        // 看图理解
        x := h.Left
        h.Left = x.Right
        if x.Right != nil {
            x.Right.Parent = h
        }
        x.Parent = h.Parent
        if h.Parent == nil {
            tree.Root = x
        } else if h.Parent.Right == h {
            h.Parent.Right = x
        } else {
            h.Parent.Left = x
        }
        x.Right = h
        h.Parent = x
    }
}

旋转作为局部调整，并不影响全局。

可以继续查看下面的内容。

2.3. 添加元素实现

每次添加元素节点时，都将该节点 Color 字段，也就是父亲指向它的链接设置为 RED 红色。

总结情况如下：

情况1：空树，那么插入节点直接变为根节点。

情况2：父节点是黑节点，直接插入即可，不破坏红黑树特征。

情况3：父节点是红节点，叔叔节点也是红节点，这时对应 2-3-4 树的4节点，插入后变成了5节点，破坏了平衡，直接将祖父节点变色即可，然后向上递归处理，相当于 2-3-4 树的4节点提升，如图：

情况4：父节点是红节点，没有叔叔或者叔叔是黑节点，插入后出现了两个连续的红链接，需要进行旋转调整，如图：

如果是顺方向连续红链接，旋转一次即可，否则需要左右旋转或者右左旋转，旋转两次。

这次我们使用非递归的形式，效率会更高（可及时跳出循环），代码实现如下：

// 普通红黑树添加元素
func (tree *RBTree) Add(value int64) {
    // 根节点为空
    if tree.Root == nil {
        // 根节点都是黑色
        tree.Root = &RBTNode{
            Value: value,
            Color: BLACK,
        }
        return
    }
    // 辅助变量 t，表示新元素要插入到该子树，t是该子树的根节点
    t := tree.Root
    // 插入元素后，插入元素的父亲节点
    var parent *RBTNode
    // 辅助变量，为了知道元素最后要插到左边还是右边
    var cmp int64 = 0
    for {
        parent = t
        cmp = value - t.Value
        if cmp < 0 {
            // 比当前节点小，往左子树插入
            t = t.Left
        } else if cmp > 0 {
            // 比当前节点节点大，往右子树插入
            t = t.Right
        } else {
            // 已经存在值了，更新出现的次数
            t.Times = t.Times + 1
            return
        }
        // 终于找到要插入的位置了
        if t == nil {
            break // 这时叶子节点是 parent，要插入到 parent 的下面，跳到外层去
        }
    }
    // 新节点，它要插入到 parent下面
    newNode := &RBTNode{
        Value:  value,
        Parent: parent,
    }
    if cmp < 0 {
        // 知道要从左边插进去
        parent.Left = newNode
    } else {
        // 知道要从右边插进去
        parent.Right = newNode
    }
    // 插入新节点后，可能破坏了红黑树特征，需要修复，核心函数
    tree.fixAfterInsertion(newNode)
}
// 调整新插入的节点，自底而上
// 可以看图理解
func (tree *RBTree) fixAfterInsertion(node *RBTNode) {
    // 插入的新节点一定要是红色
    node.Color = RED
    // 节点不能是空，不能是根节点，父亲的颜色必须为红色（如果是黑色，那么直接插入不破坏平衡，不需要调整了）
    for node != nil && node != tree.Root && node.Parent.Color == RED {
        // 父亲在祖父的左边
        if ParentOf(node) == LeftOf(ParentOf(ParentOf(node))) {
            // 叔叔节点
            uncle := RightOf(ParentOf(ParentOf(node)))
            // 图例3左边部分，叔叔是红节点，祖父变色，也就是父亲和叔叔变黑，祖父变红
            if IsRed(uncle) {
                SetColor(ParentOf(node), BLACK)
                SetColor(uncle, BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                // 还要向上递归
                node = ParentOf(ParentOf(node))
            } else {
                // 图例4左边部分，叔叔是黑节点，并且插入的节点在父亲的右边，需要对父亲左旋
                if node == RightOf(ParentOf(node)) {
                    node = ParentOf(node)
                    tree.RotateLeft(node)
                }
                // 变色，并对祖父进行右旋
                SetColor(ParentOf(node), BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                tree.RotateRight(ParentOf(ParentOf(node)))
            }
        } else {
            // 父亲在祖父的右边，与父亲在祖父的左边相似
            // 叔叔节点
            uncle := LeftOf(ParentOf(ParentOf(node)))
            // 图例3右边部分，叔叔是红节点，祖父变色，也就是父亲和叔叔变黑，祖父变红
            if IsRed(uncle) {
                SetColor(ParentOf(node), BLACK)
                SetColor(uncle, BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                // 还要向上递归
                node = ParentOf(ParentOf(node))
            } else {
                // 图例4右边部分，叔叔是黑节点，并且插入的节点在父亲的左边，需要对父亲右旋
                if node == LeftOf(ParentOf(node)) {
                    node = ParentOf(node)
                    tree.RotateRight(node)
                }
                // 变色，并对祖父进行左旋
                SetColor(ParentOf(node), BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                tree.RotateLeft(ParentOf(ParentOf(node)))
            }
        }
    }
    // 根节点永远为黑
    tree.Root.Color = BLACK
}

首先，如果是空树，那么新建根节点：

1. // 根节点为空
2. if tree.Root == nil {
3. // 根节点都是黑色
4. tree.Root = &RBTNode{
5. Value: value,
6. Color: BLACK,
7. }
8. return
9. }

否则，需要找到叶子节点，方便新节点插进去：

    // 辅助变量 t，表示新元素要插入到该子树，t是该子树的根节点
    t := tree.Root
    // 插入元素后，插入元素的父亲节点
    var parent *RBTNode
    // 辅助变量，为了知道元素最后要插到左边还是右边
    var cmp int64 = 0
    for {
        parent = t
        cmp = value - t.Value
        if cmp < 0 {
            // 比当前节点小，往左子树插入
            t = t.Left
        } else if cmp > 0 {
            // 比当前节点节点大，往右子树插入
            t = t.Right
        } else {
            // 已经存在值了，更新出现的次数
            t.Times = t.Times + 1
            return
        }
        // 终于找到要插入的位置了
        if t == nil {
            break // 这时叶子节点是 parent，要插入到 parent 的下面，跳到外层去
        }
    }

找到了要插入的位置，该位置是 parent，将新元素插入：

    // 新节点，它要插入到 parent下面
    newNode := &RBTNode{
        Value:  value,
        Parent: parent,
    }
    if cmp < 0 {
        // 知道要从左边插进去
        parent.Left = newNode
    } else {
        // 知道要从右边插进去
        parent.Right = newNode
    }

插入节点后，就需要进行调整操作了，这是核心：tree.fixAfterInsertion(newNode)。

参照图例对比一下，就可以理解调整操作的逻辑了：

// 调整新插入的节点，自底而上
// 可以看图理解
func (tree *RBTree) fixAfterInsertion(node *RBTNode) {
    // 插入的新节点一定要是红色
    node.Color = RED
    // 节点不能是空，不能是根节点，父亲的颜色必须为红色（如果是黑色，那么直接插入不破坏平衡，不需要调整了）
    for node != nil && node != tree.Root && node.Parent.Color == RED {
        // 父亲在祖父的左边
        if ParentOf(node) == LeftOf(ParentOf(ParentOf(node))) {
            // 叔叔节点
            uncle := RightOf(ParentOf(ParentOf(node)))
            // 图例3左边部分，叔叔是红节点，祖父变色，也就是父亲和叔叔变黑，祖父变红
            if IsRed(uncle) {
                SetColor(ParentOf(node), BLACK)
                SetColor(uncle, BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                // 还要向上递归
                node = ParentOf(ParentOf(node))
            } else {
                // 图例4左边部分，叔叔是黑节点，并且插入的节点在父亲的右边，需要对父亲左旋
                if node == RightOf(ParentOf(node)) {
                    node = ParentOf(node)
                    tree.RotateLeft(node)
                }
                // 变色，并对祖父进行右旋
                SetColor(ParentOf(node), BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                tree.RotateRight(ParentOf(ParentOf(node)))
            }
        } else {
            // 父亲在祖父的右边，与父亲在祖父的左边相似
            // 叔叔节点
            uncle := LeftOf(ParentOf(ParentOf(node)))
            // 图例3右边部分，叔叔是红节点，祖父变色，也就是父亲和叔叔变黑，祖父变红
            if IsRed(uncle) {
                SetColor(ParentOf(node), BLACK)
                SetColor(uncle, BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                // 还要向上递归
                node = ParentOf(ParentOf(node))
            } else {
                // 图例4右边部分，叔叔是黑节点，并且插入的节点在父亲的左边，需要对父亲右旋
                if node == LeftOf(ParentOf(node)) {
                    node = ParentOf(node)
                    tree.RotateRight(node)
                }
                // 变色，并对祖父进行左旋
                SetColor(ParentOf(node), BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                tree.RotateLeft(ParentOf(ParentOf(node)))
            }
        }
    }
    // 根节点永远为黑
    tree.Root.Color = BLACK
}

可以知道，每次新插入的节点一定是红色：node.Color = RED。

接着判断：node != nil && node != tree.Root && node.Parent.Color == RED，发现节点非空，且非根节点，并且其父亲是红色，那么插入新元素到父亲下面就连续两个红链接了，需要调整，否则不需要调整。

调整时要区分父亲是在祖父的左边：ParentOf(node) == LeftOf(ParentOf(ParentOf(node))) 还是在右边，接着判断叔叔节点uncle := RightOf(ParentOf(ParentOf(node))) 的颜色。

如果叔叔是红色，对应图例3，如图：

叔叔是红节点，那么祖父变色，也就是父亲和叔叔变黑，祖父变红，然后继续往上递归：

1. // 图例3右边部分，叔叔是红节点，祖父变色，也就是父亲和叔叔变黑，祖父变红
2. if IsRed(uncle) {
3. SetColor(ParentOf(node), BLACK)
4. SetColor(uncle, BLACK)
5. SetColor(ParentOf(ParentOf(node)), RED)
6. // 还要向上递归
7. node = ParentOf(ParentOf(node))
8. }

如果叔叔不是红色，对应图例4，如图：

在图例4左边部分，父亲在祖父左边，叔叔是黑节点，如果插入的节点在父亲的右边，需要对父亲左旋，接着对祖父变色即可：

1. // 图例4左边部分，叔叔是黑节点，并且插入的节点在父亲的右边，需要对父亲左旋
2. if node == RightOf(ParentOf(node)) {
3. node = ParentOf(node)
4. tree.RotateLeft(node)
5. }
7. // 变色，并对祖父进行右旋
8. SetColor(ParentOf(node), BLACK)
9. SetColor(ParentOf(ParentOf(node)), RED)
10. tree.RotateRight(ParentOf(ParentOf(node)))

在图例4右边部分，父亲在祖父右边，叔叔是黑节点，如果插入的节点在父亲的左边，需要对父亲右旋，接着对祖父变色即可：

1. // 图例4右边部分，叔叔是黑节点，并且插入的节点在父亲的左边，需要对父亲右旋
2. if node == LeftOf(ParentOf(node)) {
3. node = ParentOf(node)
4. tree.RotateRight(node)
5. }
7. // 变色，并对祖父进行左旋
8. SetColor(ParentOf(node), BLACK)
9. SetColor(ParentOf(ParentOf(node)), RED)
10. tree.RotateLeft(ParentOf(ParentOf(node)))

最后，调整完后，根节点永远为黑：

1. // 根节点永远为黑
2. tree.Root.Color = BLACK

2.4. 添加元素算法分析

当父亲是红节点，叔叔为空或是黑节点时，不需要向上递归，插入最多旋转两次就恢复了平衡。而如果父亲和叔叔都是红节点，那么祖父变色之后可能需要一直递归向上处理，直到根节点，但是只要中途出现了旋转，仍然是旋转两次就不需要继续向上递归，树就平衡了。

最坏情况的红黑树高度为 2log(n)（证明略），查找到插入的位置最坏情况查找 2log(n) 次，然后进行调整，最坏情况递归到根节点，递归 2log(n) 次（构造最坏情况的树很难），去掉常数，添加元素的平均时间复杂度仍然为 log(n)，而旋转最多不超过两次。

2.5. 删除元素实现

删除操作就复杂得多了。对照一下 2-3-4 树。

1. 情况1：如果删除的是非叶子节点，找到其最小后驱节点，也就是在其右子树中一直向左找，找到的该叶子节点替换被删除的节点，然后删除该叶子节点，变成情况2。
2. 情况2：如果删除的是叶子节点，如果它是红节点，也就是父亲指向它的链接为红色，那么直接删除即可。否则，我们需要进行调整，使它变为红节点，再删除。

针对情况2，如果删除的叶子节点是红节点，那它对应 2-3-4 树的3节点或4节点，直接删除即可，删除后变为了2节点或3节点。否则，它是一个2节点，删除后破坏了平衡，要么向兄弟借值，要么和父亲的一个元素合并。

删除的叶子节点是黑色的，才需要向兄弟借值，或与父亲合并，有以下几种情况：

删除的叶子节点在父亲的左边：

图例中 21， 22 相当于向兄弟借值，而 1 和 23 相当于向父亲的一个值合并后调整。

我们仔细分析一下：

图例 1，当删除的叶子节点在父亲左边，而兄弟是红色节点，我们可以知道 父亲 和 兄弟的儿子们 绝对都是黑节点，将兄弟变黑，父亲变红，然后对父亲右链接左旋。如图：

这时调整后变为了图例 23，这种情况实际上是在 2-3-4 树中和父亲的值合并，只不过将父亲的值转了一个方向，可能变为图例 21，22，23。

图例 23，当删除的叶子节点在父亲左边，兄弟节点是黑色，兄弟的儿子们也都是黑色，相当于 2-3-4 树和兄弟借不到值了，需要将兄弟变为红色，然后将父亲作为一个整体来删除，向上递归处理（相当于拉了父亲的一个值和兄弟合并）。如图：

图例 21 和 21 就简单了，相当 2-3-4 树与兄弟借值。

图例 21，当删除的叶子节点在父亲左边，且兄弟是黑色，而兄弟的右儿子是红色，那么兄弟设置成父亲的颜色，兄弟的右儿子和父亲变黑，接着对父亲进行左旋，旋转后可以直接删除元素。如图：

图例 22，当删除的叶子节点在父亲左边，且兄弟是黑色，而兄弟的右儿子是黑色，左儿子是红色，将兄弟设置为红色，兄弟的左儿子设置为黑色，对兄弟进行右旋，变为图例 21。如图：

当然，删除的叶子节点可以在父亲的右边（与上述的图反方向）：

类似于删除的叶子节点在父亲的左边，在此不再分析。

上面的图例，我们其实可以将其画出 2-3-4 树的形式，会更容易理解，在此就不画出了。

这次我们使用非递归的形式，效率会更高（可及时跳出循环），代码实现如下：

// 普通红黑树删除元素
func (tree *RBTree) Delete(value int64) {
    // 查找元素是否存在，不存在则退出
    p := tree.Find(value)
    if p == nil {
        return
    }
    // 删除该节点
    tree.delete(p)
}
// 删除节点核心函数
// 找最小后驱节点来补位，删除内部节点转为删除叶子节点
func (tree *RBTree) delete(node *RBTNode) {
    // 如果左右子树都存在，那么从右子树的左边一直找一直找，就找能到最小后驱节点
    if node.Left != nil && node.Right != nil {
        s := node.Right
        for s.Left != nil {
            s = s.Left
        }
        // 删除的叶子节点找到了，删除内部节点转为删除叶子节点
        node.Value = s.Value
        node.Times = s.Times
        node = s // 可能存在右儿子
    }
    if node.Left == nil && node.Right == nil {
        // 没有子树，要删除的节点就是叶子节点。
    } else {
        // 只有一棵子树，因为红黑树的特征，该子树就只有一个节点
        // 找到该唯一节点
        replacement := node.Left
        if node.Left == nil {
            replacement = node.Right
        }
        // 替换开始，子树的唯一节点替代被删除的内部节点
        replacement.Parent = node.Parent
        if node.Parent == nil {
            // 要删除的节点的父亲为空，表示要删除的节点为根节点，唯一子节点成为树根
            tree.Root = replacement
        } else if node == node.Parent.Left {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Left = replacement
        } else {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Right = replacement
        }
        // delete this node
        node.Parent = nil
        node.Right = nil
        node.Left = nil
        //  case 1: not enter this logic
        //      R(del)
        //    B   B
        //
        //  case 2: node's color must be black, and it's son must be red
        //    B(del)     B(del)
        //  R  O       O   R
        //
        // 单子树时删除的节点绝对是黑色的，而其唯一子节点必然是红色的
        // 现在唯一子节点替换了被删除节点，该节点要变为黑色
        // now son replace it's father, just change color to black
        replacement.Color = BLACK
        return
    }
    // 要删除的叶子节点没有父亲，那么它是根节点，直接置空，返回
    if node.Parent == nil {
        tree.Root = nil
        return
    }
    // 要删除的叶子节点，是一个黑节点，删除后会破坏平衡，需要进行调整，调整成可以删除的状态
    if !IsRed(node) {
        // 核心函数
        tree.fixAfterDeletion(node)
    }
    // 现在可以删除叶子节点了
    if node == node.Parent.Left {
        node.Parent.Left = nil
    } else if node == node.Parent.Right {
        node.Parent.Right = nil
    }
    node.Parent = nil
}
// 调整删除的叶子节点，自底向上
// 可以看图理解
func (tree *RBTree) fixAfterDeletion(node *RBTNode) {
    // 如果不是递归到根节点，且节点是黑节点，那么继续递归
    for tree.Root != node && !IsRed(node) {
        // 要删除的节点在父亲左边，对应图例1，2
        if node == LeftOf(ParentOf(node)) {
            // 找出兄弟
            brother := RightOf(ParentOf(node))
            // 兄弟是红色的，对应图例1，那么兄弟变黑，父亲变红，然后对父亲左旋，进入图例21,22,23
            if IsRed(brother) {
                SetColor(brother, BLACK)
                SetColor(ParentOf(node), RED)
                tree.RotateLeft(ParentOf(node))
                brother = RightOf(ParentOf(node)) // 图例1调整后进入图例21,22,23，兄弟此时变了
            }
            // 兄弟是黑色的，对应图例21，22，23
            // 兄弟的左右儿子都是黑色，进入图例23，将兄弟设为红色，父亲所在的子树作为整体，当作删除的节点，继续向上递归
            if !IsRed(LeftOf(brother)) && !IsRed(RightOf(brother)) {
                SetColor(brother, RED)
                node = ParentOf(node)
            } else {
                // 兄弟的右儿子是黑色，进入图例22，将兄弟设为红色，兄弟的左儿子设为黑色，对兄弟右旋，进入图例21
                if !IsRed(RightOf(brother)) {
                    SetColor(LeftOf(brother), BLACK)
                    SetColor(brother, RED)
                    tree.RotateRight(brother)
                    brother = RightOf(ParentOf(node)) // 图例22调整后进入图例21，兄弟此时变了
                }
                // 兄弟的右儿子是红色，进入图例21，将兄弟设置为父亲的颜色，兄弟的右儿子以及父亲变黑，对父亲左旋
                SetColor(brother, ParentOf(node).Color)
                SetColor(ParentOf(node), BLACK)
                SetColor(RightOf(brother), BLACK)
                tree.RotateLeft(ParentOf(node))
                node = tree.Root
            }
        } else {
            // 要删除的节点在父亲右边，对应图例3，4
            // 找出兄弟
            brother := RightOf(ParentOf(node))
            // 兄弟是红色的，对应图例3，那么兄弟变黑，父亲变红，然后对父亲右旋，进入图例41,42,43
            if IsRed(brother) {
                SetColor(brother, BLACK)
                SetColor(ParentOf(node), RED)
                tree.RotateRight(ParentOf(node))
                brother = LeftOf(ParentOf(node)) // 图例3调整后进入图例41,42,43，兄弟此时变了
            }
            // 兄弟是黑色的，对应图例41，42，43
            // 兄弟的左右儿子都是黑色，进入图例43，将兄弟设为红色，父亲所在的子树作为整体，当作删除的节点，继续向上递归
            if !IsRed(LeftOf(brother)) && !IsRed(RightOf(brother)) {
                SetColor(brother, RED)
                node = ParentOf(node)
            } else {
                // 兄弟的左儿子是黑色，进入图例42，将兄弟设为红色，兄弟的右儿子设为黑色，对兄弟左旋，进入图例41
                if !IsRed(LeftOf(brother)) {
                    SetColor(RightOf(brother), BLACK)
                    SetColor(brother, RED)
                    tree.RotateLeft(brother)
                    brother = LeftOf(ParentOf(node)) // 图例42调整后进入图例41，兄弟此时变了
                }
                // 兄弟的左儿子是红色，进入图例41，将兄弟设置为父亲的颜色，兄弟的左儿子以及父亲变黑，对父亲右旋
                SetColor(brother, ParentOf(node).Color)
                SetColor(ParentOf(node), BLACK)
                SetColor(LeftOf(brother), BLACK)
                tree.RotateRight(ParentOf(node))
                node = tree.Root
            }
        }
    }
    // this node always black
    SetColor(node, BLACK)
}

首先需要查找删除的值是否存在，不存在则不必要调用删除操作了：

// 普通红黑树删除元素
func (tree *RBTree) Delete(value int64) {
    // 查找元素是否存在，不存在则退出
    p := tree.Find(value)
    if p == nil {
        return
    }
    // 删除该节点
    tree.delete(p)
}

存在删除的节点，那么进入删除操作：tree.delete(p)。

删除操作无非就是找最小后驱节点来补位，删除内部节点转为删除叶子节点，然后针对叶子节点的链接是不是黑色，是的话那么需要调整：

// 删除节点核心函数
// 找最小后驱节点来补位，删除内部节点转为删除叶子节点
func (tree *RBTree) delete(node *RBTNode) {
    // 如果左右子树都存在，那么从右子树的左边一直找一直找，就找能到最小后驱节点
    if node.Left != nil && node.Right != nil {
        s := node.Right
        for s.Left != nil {
            s = s.Left
        }
        // 删除的叶子节点找到了，删除内部节点转为删除叶子节点
        node.Value = s.Value
        node.Times = s.Times
        node = s // 可能存在右儿子
    }
    if node.Left == nil && node.Right == nil {
        // 没有子树，要删除的节点就是叶子节点。
    } else {
        // 只有一棵子树，因为红黑树的特征，该子树就只有一个节点
        // 找到该唯一节点
        replacement := node.Left
        if node.Left == nil {
            replacement = node.Right
        }
        // 替换开始，子树的唯一节点替代被删除的内部节点
        replacement.Parent = node.Parent
        if node.Parent == nil {
            // 要删除的节点的父亲为空，表示要删除的节点为根节点，唯一子节点成为树根
            tree.Root = replacement
        } else if node == node.Parent.Left {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Left = replacement
        } else {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Right = replacement
        }
        // delete this node
        node.Parent = nil
        node.Right = nil
        node.Left = nil
        //  case 1: not enter this logic
        //      R(del)
        //    B   B
        //
        //  case 2: node's color must be black, and it's son must be red
        //    B(del)     B(del)
        //  R  O       O   R
        //
        // 单子树时删除的节点绝对是黑色的，而其唯一子节点必然是红色的
        // 现在唯一子节点替换了被删除节点，该节点要变为黑色
        // now son replace it's father, just change color to black
        replacement.Color = BLACK
        return
    }
    // 要删除的叶子节点没有父亲，那么它是根节点，直接置空，返回
    if node.Parent == nil {
        tree.Root = nil
        return
    }
    // 要删除的叶子节点，是一个黑节点，删除后会破坏平衡，需要进行调整，调整成可以删除的状态
    if !IsRed(node) {
        // 核心函数
        tree.fixAfterDeletion(node)
    }
    // 现在可以删除叶子节点了
    if node == node.Parent.Left {
        node.Parent.Left = nil
    } else if node == node.Parent.Right {
        node.Parent.Right = nil
    }
    node.Parent = nil
}

 当删除的节点有两棵子树，那么它是内部节点，找到其最小后驱节点来替换它，也就是其右子树一直往左边找，该最小后驱节点可能是叶子结点，也可能有一个右儿子：

    // 如果左右子树都存在，那么从右子树的左边一直找一直找，就找能到最小后驱节点
    if node.Left != nil && node.Right != nil {
        s := node.Right
        for s.Left != nil {
            s = s.Left
        }
        // 删除的叶子节点找到了，删除内部节点转为删除叶子节点
        node.Value = s.Value
        node.Times = s.Times
        node = s
    }

 接着继续判断，

如果没有子树，那么删除的节点就是叶子节点了：

1. if node.Left == nil && node.Right == nil {
2. // 没有子树，要删除的节点就是叶子节点。
3. }

否则如果只有一棵子树，那么根据红黑树的特征，该子树只有一个节点：

    } else {
        // 只有一棵子树，因为红黑树的特征，该子树就只有一个节点
        // 找到该唯一节点
        replacement := node.Left
        if node.Left == nil {
            replacement = node.Right
        }
        // 替换开始，子树的唯一节点替代被删除的内部节点
        replacement.Parent = node.Parent
        if node.Parent == nil {
            // 要删除的节点的父亲为空，表示要删除的节点为根节点，唯一子节点成为树根
            tree.Root = replacement
        } else if node == node.Parent.Left {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Left = replacement
        } else {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Right = replacement
        }
        // delete this node
        node.Parent = nil
        node.Right = nil
        node.Left = nil
        //  case 1: not enter this logic
        //      R(del)
        //    B   B
        //
        //  case 2: node's color must be black, and it's son must be red
        //    B(del)     B(del)
        //  R  O       O   R
        //
        // 单子树时删除的节点绝对是黑色的，而其唯一子节点必然是红色的
        // 现在唯一子节点替换了被删除节点，该节点要变为黑色
        // now son replace it's father, just change color to black
        replacement.Color = BLACK
        return
    }

删除叶子节点，如何删除呢，首先如果它是根节点，那么树就空了：

1. // 要删除的叶子节点没有父亲，那么它是根节点，直接置空，返回
2. if node.Parent == nil {
3. tree.Root = nil
4. return
5. }

否则需要判断该叶子节点是不是红节点，如果不是红节点，不能直接删除，需要调整：

1. // 要删除的叶子节点，是一个黑节点，删除后会破坏平衡，需要进行调整，调整成可以删除的状态
2. if !IsRed(node) {
3. // 核心函数
4. tree.fixAfterDeletion(node)
5. }

最后，就可以删除叶子节点了：

1. // 现在可以删除叶子节点了
2. if node == node.Parent.Left {
3. node.Parent.Left = nil
4. } else if node == node.Parent.Right {
5. node.Parent.Right = nil
6. }
7. node.Parent = nil

核心删除调整函数 fixAfterDeletion 非常重要，可以看图理解：

// 调整删除的叶子节点，自底向上
// 可以看图理解
func (tree *RBTree) fixAfterDeletion(node *RBTNode) {
    // 如果不是递归到根节点，且节点是黑节点，那么继续递归
    for tree.Root != node && !IsRed(node) {
        // 要删除的节点在父亲左边，对应图例1，2
        if node == LeftOf(ParentOf(node)) {
            // 找出兄弟
            brother := RightOf(ParentOf(node))
            // 兄弟是红色的，对应图例1，那么兄弟变黑，父亲变红，然后对父亲左旋，进入图例21,22,23
            if IsRed(brother) {
                SetColor(brother, BLACK)
                SetColor(ParentOf(node), RED)
                tree.RotateLeft(ParentOf(node))
                brother = RightOf(ParentOf(node)) // 图例1调整后进入图例21,22,23，兄弟此时变了
            }
            // 兄弟是黑色的，对应图例21，22，23
            // 兄弟的左右儿子都是黑色，进入图例23，将兄弟设为红色，父亲所在的子树作为整体，当作删除的节点，继续向上递归
            if !IsRed(LeftOf(brother)) && !IsRed(RightOf(brother)) {
                SetColor(brother, RED)
                node = ParentOf(node)
            } else {
                // 兄弟的右儿子是黑色，进入图例22，将兄弟设为红色，兄弟的左儿子设为黑色，对兄弟右旋，进入图例21
                if !IsRed(RightOf(brother)) {
                    SetColor(LeftOf(brother), BLACK)
                    SetColor(brother, RED)
                    tree.RotateRight(brother)
                    brother = RightOf(ParentOf(node)) // 图例22调整后进入图例21，兄弟此时变了
                }
                // 兄弟的右儿子是红色，进入图例21，将兄弟设置为父亲的颜色，兄弟的右儿子以及父亲变黑，对父亲左旋
                SetColor(brother, ParentOf(node).Color)
                SetColor(ParentOf(node), BLACK)
                SetColor(RightOf(brother), BLACK)
                tree.RotateLeft(ParentOf(node))
                node = tree.Root
            }
        } else {
            // 要删除的节点在父亲右边，对应图例3，4
            // 找出兄弟
            brother := RightOf(ParentOf(node))
            // 兄弟是红色的，对应图例3，那么兄弟变黑，父亲变红，然后对父亲右旋，进入图例41,42,43
            if IsRed(brother) {
                SetColor(brother, BLACK)
                SetColor(ParentOf(node), RED)
                tree.RotateRight(ParentOf(node))
                brother = LeftOf(ParentOf(node)) // 图例3调整后进入图例41,42,43，兄弟此时变了
            }
            // 兄弟是黑色的，对应图例41，42，43
            // 兄弟的左右儿子都是黑色，进入图例43，将兄弟设为红色，父亲所在的子树作为整体，当作删除的节点，继续向上递归
            if !IsRed(LeftOf(brother)) && !IsRed(RightOf(brother)) {
                SetColor(brother, RED)
                node = ParentOf(node)
            } else {
                // 兄弟的左儿子是黑色，进入图例42，将兄弟设为红色，兄弟的右儿子设为黑色，对兄弟左旋，进入图例41
                if !IsRed(LeftOf(brother)) {
                    SetColor(RightOf(brother), BLACK)
                    SetColor(brother, RED)
                    tree.RotateLeft(brother)
                    brother = LeftOf(ParentOf(node)) // 图例42调整后进入图例41，兄弟此时变了
                }
                // 兄弟的左儿子是红色，进入图例41，将兄弟设置为父亲的颜色，兄弟的左儿子以及父亲变黑，对父亲右旋
                SetColor(brother, ParentOf(node).Color)
                SetColor(ParentOf(node), BLACK)
                SetColor(LeftOf(brother), BLACK)
                tree.RotateRight(ParentOf(node))
                node = tree.Root
            }
        }
    }
    // this node always black
    SetColor(node, BLACK)
}

只有符合 tree.Root != node && !IsRed(node) 才能继续进入递归。

要删除的节点在父亲左边：node == LeftOf(ParentOf(node))，对应图例1，2:

否则对应图例3，4：

可以参考图理解代码，代码注释很清晰地对照了示例图。

2.6. 删除元素算法分析

删除元素比左倾红黑树的情况还要多，但是平均时间复杂度仍然是 log(n)，出现在和兄弟借不到值的情况下向上递归。和 AVL树 区别是，普通红黑树删除元素最多旋转三次，参考 1图例-22图例-21图例 的状态转变，最多旋转三次，而 AVL树 可能旋转很多次，甚至自底向上一直旋转到根节点。

2.7. 查找元素等实现

略。与左倾红黑树，AVL树都一样。

2.8. 验证是否是一棵普通红黑树

如何确保我们的代码实现的就是一棵普通红黑树呢，可以进行验证：

// 验证是不是棵红黑树
func (tree *RBTree) IsRBTree() bool {
    if tree == nil || tree.Root == nil {
        return true
    }
    // 判断树是否是一棵二分查找树
    if !tree.Root.IsBST() {
        return false
    }
    // 判断树是否遵循2-3-4树，也就是不能有连续的两个红链接
    if !tree.Root.Is234() {
        return false
    }
    // 判断树是否平衡，也就是任意一个节点到叶子节点，经过的黑色链接数量相同
    // 先计算根节点到最左边叶子节点的黑链接数量
    blackNum := 0
    x := tree.Root
    for x != nil {
        if !IsRed(x) { // 是黑色链接
            blackNum = blackNum + 1
        }
        x = x.Left
    }
    if !tree.Root.IsBalanced(blackNum) {
        return false
    }
    return true
}
// 节点所在的子树是否是一棵二分查找树
func (node *RBTNode) IsBST() bool {
    if node == nil {
        return true
    }
    // 左子树非空，那么根节点必须大于左儿子节点
    if node.Left != nil {
        if node.Value > node.Left.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 右子树非空，那么根节点必须小于右儿子节点
    if node.Right != nil {
        if node.Value < node.Right.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 左子树也要判断是否是平衡查找树
    if !node.Left.IsBST() {
        return false
    }
    // 右子树也要判断是否是平衡查找树
    if !node.Right.IsBST() {
        return false
    }
    return true
}
// 节点所在的子树是否遵循2-3-4树
func (node *RBTNode) Is234() bool {
    if node == nil {
        return true
    }
    // 不允许连续两个左红链接
    if IsRed(node) && IsRed(node.Left) {
        fmt.Printf("father:%#v,lchild:%#v\n", node, node.Left)
        return false
    }
    if IsRed(node) && IsRed(node.Right) {
        fmt.Printf("father:%#v,rchild:%#v\n", node, node.Right)
        return false
    }
    // 左子树也要判断是否遵循2-3-4树
    if !node.Left.Is234() {
        return false
    }
    // 右子树也要判断是否是遵循2-3-4树
    if !node.Right.Is234() {
        return false
    }
    return true
}
// 节点所在的子树是否平衡，是否有 blackNum 个黑链接
func (node *RBTNode) IsBalanced(blackNum int) bool {
    if node == nil {
        return blackNum == 0
    }
    if !IsRed(node) {
        blackNum = blackNum - 1
    }
    if !node.Left.IsBalanced(blackNum) {
        fmt.Println("node.Left to leaf black link is not ", blackNum)
        return false
    }
    if !node.Right.IsBalanced(blackNum) {
        fmt.Println("node.Right to leaf black link is not ", blackNum)
        return false
    }
    return true
}

运行请看完整代码。

2.9. 完整程序

package main
import "fmt"
// 普通红黑树实现，参考 Java TreeMap，更强壮。
// red-black tree
// 定义颜色
const (
    RED   = true
    BLACK = false
)
// 普通红黑树
type RBTree struct {
    Root *RBTNode // 树根节点
}
// 新建一棵空树
func NewRBTree() *RBTree {
    return &RBTree{}
}
// 普通红黑树节点
type RBTNode struct {
    Value  int64    // 值
    Times  int64    // 值出现的次数
    Left   *RBTNode // 左子树
    Right  *RBTNode // 右子树
    Parent *RBTNode // 父节点
    Color  bool     // 父亲指向该节点的链接颜色
}
// 节点的颜色
func IsRed(node *RBTNode) bool {
    if node == nil {
        return false
    }
    return node.Color == RED
}
// 返回节点的父亲节点
func ParentOf(node *RBTNode) *RBTNode {
    if node == nil {
        return nil
    }
    return node.Parent
}
// 返回节点的左子节点
func LeftOf(node *RBTNode) *RBTNode {
    if node == nil {
        return nil
    }
    return node.Left
}
// 返回节点的右子节点
func RightOf(node *RBTNode) *RBTNode {
    if node == nil {
        return nil
    }
    return node.Right
}
// 设置节点颜色
func SetColor(node *RBTNode, color bool) {
    if node != nil {
        node.Color = color
    }
}
// 对某节点左旋转
func (tree *RBTree) RotateLeft(h *RBTNode) {
    if h != nil {
        // 看图理解
        x := h.Right
        h.Right = x.Left
        if x.Left != nil {
            x.Left.Parent = h
        }
        x.Parent = h.Parent
        if h.Parent == nil {
            tree.Root = x
        } else if h.Parent.Left == h {
            h.Parent.Left = x
        } else {
            h.Parent.Right = x
        }
        x.Left = h
        h.Parent = x
    }
}
// 对某节点右旋转
func (tree *RBTree) RotateRight(h *RBTNode) {
    if h != nil {
        // 看图理解
        x := h.Left
        h.Left = x.Right
        if x.Right != nil {
            x.Right.Parent = h
        }
        x.Parent = h.Parent
        if h.Parent == nil {
            tree.Root = x
        } else if h.Parent.Right == h {
            h.Parent.Right = x
        } else {
            h.Parent.Left = x
        }
        x.Right = h
        h.Parent = x
    }
}
// 普通红黑树添加元素
func (tree *RBTree) Add(value int64) {
    // 根节点为空
    if tree.Root == nil {
        // 根节点都是黑色
        tree.Root = &RBTNode{
            Value: value,
            Color: BLACK,
        }
        return
    }
    // 辅助变量 t，表示新元素要插入到该子树，t是该子树的根节点
    t := tree.Root
    // 插入元素后，插入元素的父亲节点
    var parent *RBTNode
    // 辅助变量，为了知道元素最后要插到左边还是右边
    var cmp int64 = 0
    for {
        parent = t
        cmp = value - t.Value
        if cmp < 0 {
            // 比当前节点小，往左子树插入
            t = t.Left
        } else if cmp > 0 {
            // 比当前节点节点大，往右子树插入
            t = t.Right
        } else {
            // 已经存在值了，更新出现的次数
            t.Times = t.Times + 1
            return
        }
        // 终于找到要插入的位置了
        if t == nil {
            break // 这时叶子节点是 parent，要插入到 parent 的下面，跳到外层去
        }
    }
    // 新节点，它要插入到 parent下面
    newNode := &RBTNode{
        Value:  value,
        Parent: parent,
    }
    if cmp < 0 {
        // 知道要从左边插进去
        parent.Left = newNode
    } else {
        // 知道要从右边插进去
        parent.Right = newNode
    }
    // 插入新节点后，可能破坏了红黑树特征，需要修复，核心函数
    tree.fixAfterInsertion(newNode)
}
// 调整新插入的节点，自底而上
// 可以看图理解
func (tree *RBTree) fixAfterInsertion(node *RBTNode) {
    // 插入的新节点一定要是红色
    node.Color = RED
    // 节点不能是空，不能是根节点，父亲的颜色必须为红色（如果是黑色，那么直接插入不破坏平衡，不需要调整了）
    for node != nil && node != tree.Root && node.Parent.Color == RED {
        // 父亲在祖父的左边
        if ParentOf(node) == LeftOf(ParentOf(ParentOf(node))) {
            // 叔叔节点
            uncle := RightOf(ParentOf(ParentOf(node)))
            // 图例3左边部分，叔叔是红节点，祖父变色，也就是父亲和叔叔变黑，祖父变红
            if IsRed(uncle) {
                SetColor(ParentOf(node), BLACK)
                SetColor(uncle, BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                // 还要向上递归
                node = ParentOf(ParentOf(node))
            } else {
                // 图例4左边部分，叔叔是黑节点，并且插入的节点在父亲的右边，需要对父亲左旋
                if node == RightOf(ParentOf(node)) {
                    node = ParentOf(node)
                    tree.RotateLeft(node)
                }
                // 变色，并对祖父进行右旋
                SetColor(ParentOf(node), BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                tree.RotateRight(ParentOf(ParentOf(node)))
            }
        } else {
            // 父亲在祖父的右边，与父亲在祖父的左边相似
            // 叔叔节点
            uncle := LeftOf(ParentOf(ParentOf(node)))
            // 图例3右边部分，叔叔是红节点，祖父变色，也就是父亲和叔叔变黑，祖父变红
            if IsRed(uncle) {
                SetColor(ParentOf(node), BLACK)
                SetColor(uncle, BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                // 还要向上递归
                node = ParentOf(ParentOf(node))
            } else {
                // 图例4右边部分，叔叔是黑节点，并且插入的节点在父亲的左边，需要对父亲右旋
                if node == LeftOf(ParentOf(node)) {
                    node = ParentOf(node)
                    tree.RotateRight(node)
                }
                // 变色，并对祖父进行左旋
                SetColor(ParentOf(node), BLACK)
                SetColor(ParentOf(ParentOf(node)), RED)
                tree.RotateLeft(ParentOf(ParentOf(node)))
            }
        }
    }
    // 根节点永远为黑
    tree.Root.Color = BLACK
}
// 普通红黑树删除元素
func (tree *RBTree) Delete(value int64) {
    // 查找元素是否存在，不存在则退出
    p := tree.Find(value)
    if p == nil {
        return
    }
    // 删除该节点
    tree.delete(p)
}
// 删除节点核心函数
// 找最小后驱节点来补位，删除内部节点转为删除叶子节点
func (tree *RBTree) delete(node *RBTNode) {
    // 如果左右子树都存在，那么从右子树的左边一直找一直找，就找能到最小后驱节点
    if node.Left != nil && node.Right != nil {
        s := node.Right
        for s.Left != nil {
            s = s.Left
        }
        // 删除的叶子节点找到了，删除内部节点转为删除叶子节点
        node.Value = s.Value
        node.Times = s.Times
        node = s // 可能存在右儿子
    }
    if node.Left == nil && node.Right == nil {
        // 没有子树，要删除的节点就是叶子节点。
    } else {
        // 只有一棵子树，因为红黑树的特征，该子树就只有一个节点
        // 找到该唯一节点
        replacement := node.Left
        if node.Left == nil {
            replacement = node.Right
        }
        // 替换开始，子树的唯一节点替代被删除的内部节点
        replacement.Parent = node.Parent
        if node.Parent == nil {
            // 要删除的节点的父亲为空，表示要删除的节点为根节点，唯一子节点成为树根
            tree.Root = replacement
        } else if node == node.Parent.Left {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Left = replacement
        } else {
            // 子树的唯一节点替代被删除的内部节点
            node.Parent.Right = replacement
        }
        // delete this node
        node.Parent = nil
        node.Right = nil
        node.Left = nil
        //  case 1: not enter this logic
        //      R(del)
        //    B   B
        //
        //  case 2: node's color must be black, and it's son must be red
        //    B(del)     B(del)
        //  R  O       O   R
        //
        // 单子树时删除的节点绝对是黑色的，而其唯一子节点必然是红色的
        // 现在唯一子节点替换了被删除节点，该节点要变为黑色
        // now son replace it's father, just change color to black
        replacement.Color = BLACK
        return
    }
    // 要删除的叶子节点没有父亲，那么它是根节点，直接置空，返回
    if node.Parent == nil {
        tree.Root = nil
        return
    }
    // 要删除的叶子节点，是一个黑节点，删除后会破坏平衡，需要进行调整，调整成可以删除的状态
    if !IsRed(node) {
        // 核心函数
        tree.fixAfterDeletion(node)
    }
    // 现在可以删除叶子节点了
    if node == node.Parent.Left {
        node.Parent.Left = nil
    } else if node == node.Parent.Right {
        node.Parent.Right = nil
    }
    node.Parent = nil
}
// 调整删除的叶子节点，自底向上
// 可以看图理解
func (tree *RBTree) fixAfterDeletion(node *RBTNode) {
    // 如果不是递归到根节点，且节点是黑节点，那么继续递归
    for tree.Root != node && !IsRed(node) {
        // 要删除的节点在父亲左边，对应图例1，2
        if node == LeftOf(ParentOf(node)) {
            // 找出兄弟
            brother := RightOf(ParentOf(node))
            // 兄弟是红色的，对应图例1，那么兄弟变黑，父亲变红，然后对父亲左旋，进入图例21,22,23
            if IsRed(brother) {
                SetColor(brother, BLACK)
                SetColor(ParentOf(node), RED)
                tree.RotateLeft(ParentOf(node))
                brother = RightOf(ParentOf(node)) // 图例1调整后进入图例21,22,23，兄弟此时变了
            }
            // 兄弟是黑色的，对应图例21，22，23
            // 兄弟的左右儿子都是黑色，进入图例23，将兄弟设为红色，父亲所在的子树作为整体，当作删除的节点，继续向上递归
            if !IsRed(LeftOf(brother)) && !IsRed(RightOf(brother)) {
                SetColor(brother, RED)
                node = ParentOf(node)
            } else {
                // 兄弟的右儿子是黑色，进入图例22，将兄弟设为红色，兄弟的左儿子设为黑色，对兄弟右旋，进入图例21
                if !IsRed(RightOf(brother)) {
                    SetColor(LeftOf(brother), BLACK)
                    SetColor(brother, RED)
                    tree.RotateRight(brother)
                    brother = RightOf(ParentOf(node)) // 图例22调整后进入图例21，兄弟此时变了
                }
                // 兄弟的右儿子是红色，进入图例21，将兄弟设置为父亲的颜色，兄弟的右儿子以及父亲变黑，对父亲左旋
                SetColor(brother, ParentOf(node).Color)
                SetColor(ParentOf(node), BLACK)
                SetColor(RightOf(brother), BLACK)
                tree.RotateLeft(ParentOf(node))
                node = tree.Root
            }
        } else {
            // 要删除的节点在父亲右边，对应图例3，4
            // 找出兄弟
            brother := RightOf(ParentOf(node))
            // 兄弟是红色的，对应图例3，那么兄弟变黑，父亲变红，然后对父亲右旋，进入图例41,42,43
            if IsRed(brother) {
                SetColor(brother, BLACK)
                SetColor(ParentOf(node), RED)
                tree.RotateRight(ParentOf(node))
                brother = LeftOf(ParentOf(node)) // 图例3调整后进入图例41,42,43，兄弟此时变了
            }
            // 兄弟是黑色的，对应图例41，42，43
            // 兄弟的左右儿子都是黑色，进入图例43，将兄弟设为红色，父亲所在的子树作为整体，当作删除的节点，继续向上递归
            if !IsRed(LeftOf(brother)) && !IsRed(RightOf(brother)) {
                SetColor(brother, RED)
                node = ParentOf(node)
            } else {
                // 兄弟的左儿子是黑色，进入图例42，将兄弟设为红色，兄弟的右儿子设为黑色，对兄弟左旋，进入图例41
                if !IsRed(LeftOf(brother)) {
                    SetColor(RightOf(brother), BLACK)
                    SetColor(brother, RED)
                    tree.RotateLeft(brother)
                    brother = LeftOf(ParentOf(node)) // 图例42调整后进入图例41，兄弟此时变了
                }
                // 兄弟的左儿子是红色，进入图例41，将兄弟设置为父亲的颜色，兄弟的左儿子以及父亲变黑，对父亲右旋
                SetColor(brother, ParentOf(node).Color)
                SetColor(ParentOf(node), BLACK)
                SetColor(LeftOf(brother), BLACK)
                tree.RotateRight(ParentOf(node))
                node = tree.Root
            }
        }
    }
    // this node always black
    SetColor(node, BLACK)
}
// 找出最小值的节点
func (tree *RBTree) FindMinValue() *RBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMinValue()
}
func (node *RBTNode) FindMinValue() *RBTNode {
    // 左子树为空，表面已经是最左的节点了，该值就是最小值
    if node.Left == nil {
        return node
    }
    // 一直左子树递归
    return node.Left.FindMinValue()
}
// 找出最大值的节点
func (tree *RBTree) FindMaxValue() *RBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.FindMaxValue()
}
func (node *RBTNode) FindMaxValue() *RBTNode {
    // 右子树为空，表面已经是最右的节点了，该值就是最大值
    if node.Right == nil {
        return node
    }
    // 一直右子树递归
    return node.Right.FindMaxValue()
}
// 查找指定节点
func (tree *RBTree) Find(value int64) *RBTNode {
    if tree.Root == nil {
        // 如果是空树，返回空
        return nil
    }
    return tree.Root.Find(value)
}
func (node *RBTNode) Find(value int64) *RBTNode {
    if value == node.Value {
        // 如果该节点刚刚等于该值，那么返回该节点
        return node
    } else if value < node.Value {
        // 如果查找的值小于节点值，从节点的左子树开始找
        if node.Left == nil {
            // 左子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Left.Find(value)
    } else {
        // 如果查找的值大于节点值，从节点的右子树开始找
        if node.Right == nil {
            // 右子树为空，表示找不到该值了，返回nil
            return nil
        }
        return node.Right.Find(value)
    }
}
// 中序遍历
func (tree *RBTree) MidOrder() {
    tree.Root.MidOrder()
}
func (node *RBTNode) MidOrder() {
    if node == nil {
        return
    }
    // 先打印左子树
    node.Left.MidOrder()
    // 按照次数打印根节点
    for i := 0; i <= int(node.Times); i++ {
        fmt.Println(node.Value)
    }
    // 打印右子树
    node.Right.MidOrder()
}
// 验证是不是棵红黑树
func (tree *RBTree) IsRBTree() bool {
    if tree == nil || tree.Root == nil {
        return true
    }
    // 判断树是否是一棵二分查找树
    if !tree.Root.IsBST() {
        return false
    }
    // 判断树是否遵循2-3-4树，也就是不能有连续的两个红链接
    if !tree.Root.Is234() {
        return false
    }
    // 判断树是否平衡，也就是任意一个节点到叶子节点，经过的黑色链接数量相同
    // 先计算根节点到最左边叶子节点的黑链接数量
    blackNum := 0
    x := tree.Root
    for x != nil {
        if !IsRed(x) { // 是黑色链接
            blackNum = blackNum + 1
        }
        x = x.Left
    }
    if !tree.Root.IsBalanced(blackNum) {
        return false
    }
    return true
}
// 节点所在的子树是否是一棵二分查找树
func (node *RBTNode) IsBST() bool {
    if node == nil {
        return true
    }
    // 左子树非空，那么根节点必须大于左儿子节点
    if node.Left != nil {
        if node.Value > node.Left.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 右子树非空，那么根节点必须小于右儿子节点
    if node.Right != nil {
        if node.Value < node.Right.Value {
        } else {
            fmt.Printf("father:%#v,lchild:%#v,rchild:%#v\n", node, node.Left, node.Right)
            return false
        }
    }
    // 左子树也要判断是否是平衡查找树
    if !node.Left.IsBST() {
        return false
    }
    // 右子树也要判断是否是平衡查找树
    if !node.Right.IsBST() {
        return false
    }
    return true
}
// 节点所在的子树是否遵循2-3-4树
func (node *RBTNode) Is234() bool {
    if node == nil {
        return true
    }
    // 不允许连续两个左红链接
    if IsRed(node) && IsRed(node.Left) {
        fmt.Printf("father:%#v,lchild:%#v\n", node, node.Left)
        return false
    }
    if IsRed(node) && IsRed(node.Right) {
        fmt.Printf("father:%#v,rchild:%#v\n", node, node.Right)
        return false
    }
    // 左子树也要判断是否遵循2-3-4树
    if !node.Left.Is234() {
        return false
    }
    // 右子树也要判断是否是遵循2-3-4树
    if !node.Right.Is234() {
        return false
    }
    return true
}
// 节点所在的子树是否平衡，是否有 blackNum 个黑链接
func (node *RBTNode) IsBalanced(blackNum int) bool {
    if node == nil {
        return blackNum == 0
    }
    if !IsRed(node) {
        blackNum = blackNum - 1
    }
    if !node.Left.IsBalanced(blackNum) {
        fmt.Println("node.Left to leaf black link is not ", blackNum)
        return false
    }
    if !node.Right.IsBalanced(blackNum) {
        fmt.Println("node.Right to leaf black link is not ", blackNum)
        return false
    }
    return true
}
func main() {
    tree := NewRBTree()
    values := []int64{2, 3, 7, 10, 10, 10, 10, 23, 9, 102, 109, 111, 112, 113}
    for _, v := range values {
        tree.Add(v)
    }
    // 找到最大值或最小值的节点
    fmt.Println("find min value:", tree.FindMinValue())
    fmt.Println("find max value:", tree.FindMaxValue())
    // 查找不存在的99
    node := tree.Find(99)
    if node != nil {
        fmt.Println("find it 99!")
    } else {
        fmt.Println("not find it 99!")
    }
    // 查找存在的9
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    tree.MidOrder()
    // 删除存在的9后，再查找9
    tree.Delete(9)
    tree.Delete(10)
    tree.Delete(2)
    tree.Delete(3)
    tree.Add(4)
    tree.Add(3)
    tree.Add(10)
    tree.Delete(111)
    node = tree.Find(9)
    if node != nil {
        fmt.Println("find it 9!")
    } else {
        fmt.Println("not find it 9!")
    }
    if tree.IsRBTree() {
        fmt.Println("is a rb tree")
    } else {
        fmt.Println("is not rb tree")
    }
    tree.Delete(3)
    tree.Delete(4)
    tree.Delete(7)
    tree.Delete(10)
    tree.Delete(23)
    tree.Delete(102)
    tree.Delete(109)
    tree.Delete(112)
    tree.Delete(112)
    tree.MidOrder()
}

红黑树，无论是左偏还是普通的红黑树，理解都可以直接理解2-3或2-3-4树，添加操作比较简单，删除则是向兄弟借值或和父亲合并，然后如果父亲空了，把父亲的子树当成删除的一个整体，继续递归向上，至于二叉化的调整实现，则是将3或4节点画成红链接，可以多画下图就理解了。

三、应用场景

红黑树可以用来作为字典 Map 的基础数据结构，可以存储键值对，然后通过一个键，可以快速找到键对应的值，相比哈希表查找，不需要占用额外的空间。我们以上的代码实现只有 value，没有 key:value，可以简单改造实现字典。

Java 语言基础类库中的 HashMap，TreeSet，TreeMap 都有使用到，C++ 语言的 STL 标准模板库中，map 和 set 类也有使用到。很多中间件也有使用到，比如 Nginx，但 Golang 语言标准库并没有它。