图的遍历——深度优先遍历与广度优先遍历
目录
何谓遍历?
图的遍历特点
图的遍历方式
深度优先搜索
过程分析
案例分析:
算法的代码实现
测试案例:
测试结果如下:
遍历非连通图
算法复杂度分析
额外补充
广度优先搜索
过程分析
辅助队列
算法的代码实现
队列部分
广度搜索部分
测试案例:
测试结果:
非连通图的代码实现
算法复杂度分析
何谓遍历?
与树的遍历类似,图的遍历指对图中的每一个顶点都访问且仅仅访问一次。
图的遍历特点
与树的遍历以访问到NULL结点为结束标志不同,由于任意一个图的顶点都可能与其他顶点相邻接,即在访问某个顶点后,沿着某条路径一直搜索下去,有可能会回到原来顶点的位置上,即图的回路有可能会对图的遍历造成影响。为了避免这种影响,搜索中都会设置一个辅助数组记录某个顶点是否已被访问过。
图的遍历方式
图的遍历方式分为:深度优先搜索与广度优先搜索,由于图的存储结构不同,会导致搜索算法的设计思路略微不同。在此,用深度优先搜索邻接矩阵存储的无向网,以及用广度优先搜索邻接表存储的无向网。顶点的坐标从0开始。
深度优先搜索
过程分析
对于一个连通图而言,其深度优先搜索过程如下:
- 选取图中某一个顶点为搜索起点,访问该顶点;
- 访问该起点的邻接点,并以其邻接点为新的起点,重复上述步骤,直到刚刚访问过的起点不再存在没有被访问过的邻接点;
- 返回到上一个刚刚被访问过的顶点,紧接着访问其没有被访问过的邻接点;
- 重复(2)与(3)的步骤,直到所有的顶点都被访问过一遍,搜索结束。
可见,深度优先搜索类似于树的先序遍历,同样使用递归算法来实现。同时,搜索的顺序结果也是不唯一的。
案例分析:
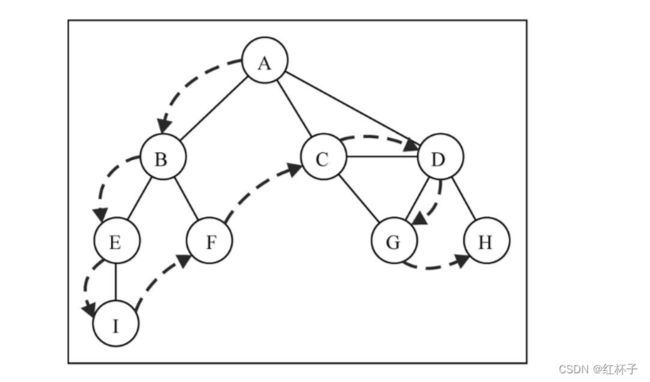
如图采用深度优先搜索的遍历顶点顺序如下:
- 先访问顶点A,紧接着访问顶点A的邻接点B,重复搜索的过程(2)直到访问到顶点I,再也没有邻接点可以访问;
- 从顶点I回溯到顶点B,发现B依旧有未被访问的邻接点F,访问顶点F;
- 然后回溯到A,发现A依旧有未被访问过的邻接点C,访问顶点C;
- 重复搜索的过程(2)直到访问到顶点G,再也没有邻接点可以访问;
- 回溯到顶点D,发现D依旧有没被访问过的邻接点H,访问H;
- 所有的顶点都被访问过,搜索结束,搜索顶点的顺序如上图所示。
算法的代码实现
AMGraph数据结构链接:http://t.csdn.cn/7SBwO
//文件名:DFS.h
#pragma once
#include
using namespace std;
//实现邻接矩阵的搜索算法
void DFS_AM(AMGraph& G, int v);
//遍历非连通图
void DFS_AMTraverse(AMGraph& G); //文件名:DFS.cpp
include"DFS.h"
#include"AMGraph.h"
//深度遍历搜索遍历邻接矩阵
void DFS_AM(AMGraph& G, int v)
{
//由于邻接矩阵查找邻接点过于简单,无需再定义Firstvex与Nextvex
//访问v结点,并输出其数据
cout << "顶点编号为:" << v << " 顶点数据域:" << G.vexs[v] << endl;
//并标记该顶点
visited[v] = true;
for (int i = 0;i < G.vexnum;i++)
{
//查找与v相互连通的顶点
if (G.arcs[v][i] != 0 && !visited[i])
{
DFS_AM(G, i);
}
}
}测试案例:
//文件名为:text.cpp
#include"DFS.h"
#include"AMGraph.h"
int main()
{
//创建邻接矩阵
AMGraph G;
CreateUDN(G);
//从下标为0号的顶点开始遍历
DFS_AM(G,0);
return 0;
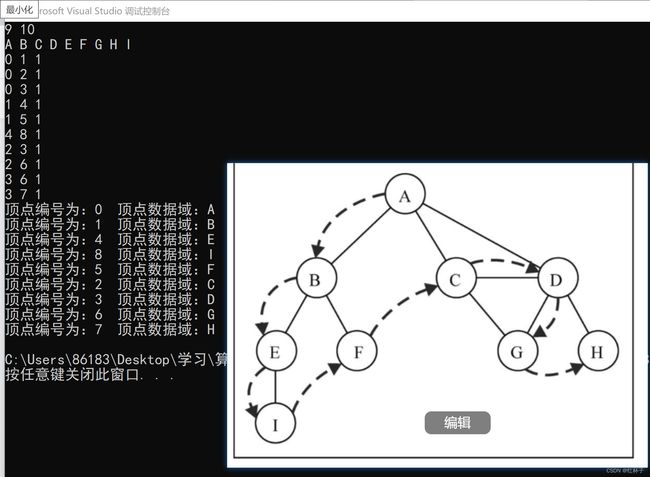
}测试结果如下:
遍历非连通图
只需要对图中的每一个顶点都做一次深度优先搜索即可,添加代码如下:
//文件名为:DFS.cpp
void DFS_AMTraverse(AMGraph& G)
{
for (int i = 0;i < G.vexnum;i++)
{
if(!visited[i])
DFS_AM(G, i);
}
}算法复杂度分析
由于遍历邻接矩阵存储的无向图实际就是遍历各个顶点。在邻接矩阵中,访问每一个顶点的所有邻接点都需要扫描n次,对于扫描n个顶点的所有邻接点,扫描总次数为n^2次,因此时间复杂度为O(n^2);由于搜索过程中,借助了辅助数组visited[n],因此空间复杂度为O(n);很明显,邻接矩阵适合稠密图,否则会判断过多无用的非邻接点。
额外补充
深度优先搜索邻接表的过程与邻接矩阵类似,通过边来找邻接点,然后对该邻接点做深度优先搜索,直到无边位置。如表的顶点数为n,边数为e,那么时间复杂度为O(n+e)。
广度优先搜索
过程分析
对于一个连通图而言,其广度优先搜索过程如下:
- 从图中的某一个顶点v出发,访问v;
- 紧接着,访问v的所有未曾访问过的邻接点;
- 然后,访问这些邻接点的所有未曾访问过的邻接点,重复上述过程,要求“先被访问的邻接点的邻接点访问”先于“后被邻接点访问的邻接点访问”,直到所有顶点都被访问。
辅助队列
细细品味,广度优先搜索与二叉树的层序遍历相似,因此可以借助队列实现上述遍历效果:
- 先将某个顶点v入队;
- 紧接着让v出队并访问该顶点,同时将其所有未曾入队的邻接点入队;
- 依照队列顺序,逐一将队列中的顶点出队并访问,同时还需要将出队顶点未曾入队的邻接点入队;
- 重复过程(3),直到队列为空,遍历结束
算法的代码实现
ALGraph数据结构链接: http://t.csdn.cn/uzDhf
队列部分
//文件名为:ALQue.h
#pragma once
#include
using namespace std;
/*
采用队列辅助实现算法
先将第一个顶点入队,当其出队时,将其所有邻接点入队,再继续出队入队
直到队列为空
*/
//队列实现
typedef struct ALQue {
//随便给个20把,毕竟设为Mvnum太浪费空间了
int Que[20];//存放入队的顶点编号
int front, rear;
int maxsize; //队列的最大长度
}ALQue;
//入队、出队(需要弹出元素)、判空、初始化
void ALQueinit(ALQue& Q);
//判断是否为空
bool is_emptys(const ALQue& Q);
//判断是否为满
bool is_full(const ALQue& Q);
//入队
void ALQ_Push(ALQue& Q, const int& v);
//出队
void ALQ_Pop(ALQue& Q, int& w); //文件名:ALQue.cpp
#include"ALQue.h"
#include"ALGraph.h"
//队列函数实现
//初始化
void ALQueinit(ALQue& Q)
{
Q.maxsize = Mvnum;
Q.front = Q.rear = 0;
}
//判断是否为空
bool is_emptys(const ALQue& Q)
{
if (Q.front == Q.rear)
return true;
else
return false;
}
//判断是否为满
bool is_full(const ALQue& Q)
{
if ((Q.rear + 1) % Q.maxsize == Q.front)
{
cout << "队列已满" << endl;
return true;
}
else
return false;
}
//入队,无需返回值
void ALQ_Push(ALQue& Q, const int& v)
{
//v为下标
if (is_full(Q))
{
return;
}
Q.Que[Q.rear] = v;
Q.rear = (Q.rear + 1) % Q.maxsize;
}
//出队
void ALQ_Pop(ALQue& Q, int& w)
{
if (is_emptys(Q))
{
return;
}
Q.rear--;
w = Q.Que[Q.rear];
}
//队列函数实现广度搜索部分
//文件名为:BFS.h
#include"ALGraph.h"
#include"ALQue.h"
/*
算法核心思想:对于连通图而言,先访问第一个顶点,
再访问该顶点的所有邻接点,再访问该顶点所有邻接点的所有
邻接点,如此循环重复,直到所有的顶点都被遍历
*/
//广度优先搜索
void BFS_AL(const ALGraph& G, const int v);
//遍历非连通图
void BFS_ALTraverse(const ALGraph& G);//文件名:BFS.cpp
#include"BFS.h"
//广度优先搜索
void BFS_AL(const ALGraph& G,const int v)
{
ALQue Q;//创建队列
ALQueinit(Q);
//访问该顶点并输出其数据域
visited[v] = true;
//先将顶点v入队,并且将入队视为已被访问的标志
ALQ_Push(Q, v);
while (!is_emptys(Q))
{
int u; //存储顶点编号
ALQ_Pop(Q, u);//出队,并将与u相互邻接的顶点入队
cout << "顶点编号为:" << u << " 其数据域:" << G.vertices[u].data << endl;
//除非查找过程的代码量巨大,否则两个查找函数就显得有点多余
//for (w = FirstAdject(G, u);w >= 0;w = NextAdject(G, u, w));
ArcNode* p = G.vertices[u].fisrtarc;
while (p)
{
//当u的邻接点的还没有入队时,则将其入队
if (!visited[p->adjvex])
{
ALQ_Push(Q, p->adjvex);
visited[p->adjvex] = true;
}
p = p->nextarc;
}
}
}
//遍历非连通图
void BFS_ALTraverse(const ALGraph& G)
{
//最坏的情况是所有的顶点的不连通,因此下标需要从0开始
for (int i = 0;i < G.vexnum;i++)
{
if(!visited[i])
BFS_AL(G, i);
}
}测试案例:
//文件名:test.cpp
#include"BFS.h"
int main()
{
ALGraph G;
CreateUDNal(G);
BFS_AL(G, 0);
DelUDNal(G);
return 0;
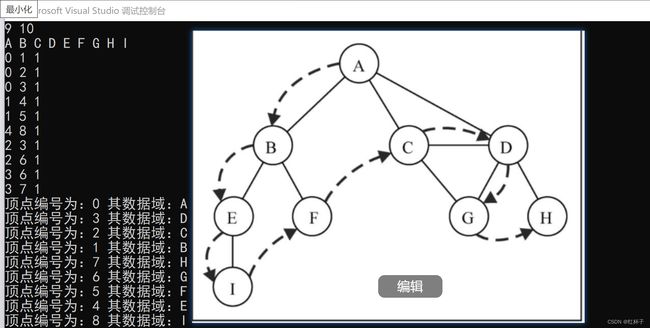
}测试结果:
非连通图的代码实现
只需要对每一个顶点都做一次广度优先搜索。
//文件名为:BFS.cpp
//遍历非连通图
void BFS_ALTraverse(const ALGraph& G)
{
//最坏的情况是所有的顶点的不连通,因此下标需要从0开始
for (int i = 0;i < G.vexnum;i++)
{
if(!visited[i])
BFS_AL(G, i);
}
}算法复杂度分析
广度优先所搜的本质同样是将每一个顶点都访问一边。对于邻接表的访问而言,需要先依次访问表头结点表中的n个顶点,紧接着访问每一个顶点所在单链表的边,总共有e条边,则访问的边数为2e次(无向网而言),故时间复杂度为O(n+2e)。同时,由于辅助数组的使用,故空间复杂度为O(n);可见,邻接表比较适合稀疏图,算法的复杂度与图的存储结构有关。