算法——排序
排序
下面的代码会用到宏定义,因为再C中没有swap交换函数,所以对于swap的宏定义代码如下:
#define swap(a, b) {\ __typeof(a) __a = a; a = b; b = __a;\ }
稳定排序:
1.插入排序:
插入排序会将数组,分位两个部分,一般分为前后两部分,而前半部分为已排序区,后半部分为未排序区;插入排序的操作就是把,未排序区中的元素插入到已排序区中的去,并且满足排序区的单调性;如图下面的操作,实现一个单调递增序列:
数组的原本样子,现在使位置0是已排序区,先去从位置1开始去插入;
将12插入到23前面,使位置0,1形成单调递增;
进行插入,对位置2插入,发现不用插入,直接对下一个位置进行插入:
位置4也不用进行插入保持原位置,对位置5进行插入:
最后完成排序;
时间复杂度:
代码实现:
void insert_sort(int *arr, int n) {//arr排序数组,n数组长度 for (int i = 1; i < n; i++) {//位置0开始定为已排序区 for (int j = i; j >= 1 && arr[j] < arr[j - 1]; j--) {//将位置i进行插入到前面的以排序区 swap(arr[j], arr[j - 1]);//交换位置 } } return ; }2.冒泡排序:
冒泡排序,为什么会叫冒泡排序,假如实现单调递增序列,那么每一次都会将未排序中的最大的元素放到未排序区中的最后去,把数组立起来数组的最后的位置在上,那么是不是每次未排序的最大元素会像冒泡一样往上升,所以叫冒泡排序;
第一次冒泡:
第一次完冒泡后,最大的元素已经放到了数组最后位置,也相当于放到了已排序区中了;然后这样一直循环直到排完序;
时间复杂度:
代码实现:
做了一个小小的优化;
void bubble_sort(int *arr, int n) { int time = 1;//用来标记这次循环是否发生了冒泡交换 for (int i = 1; i < n && time; i++) {//如果没有发生交换说明数组已经排好了序 time = 0; for (int j = 0; j < n - i; j++) { if (arr[j] >= arr[j + 1]) { swap(arr[j], arr[j + 1]); time++; } } } return ; }3.归并排序:
将一个数组从中间分开,然后通过递归一直将子数组进行分开,直到数组只有两个元素,然后通过回溯的过程中进行排序,然后一直回溯到整个数组并拢,完成排序;
然后从下往上进行排序,单调递增:
合并,排序:
合并,在排序:
最终完成排序;
时间复杂度:
代码实现:
这个过程比较容易理解,就是代码实现有那么一点复杂,来看代码:
void merge_sort(int *arr, int l, int r) {//数组的头位置,r数组的末尾在 if (r - l <= 1) {//当分到只有2个元素和1个元素时,递归出口 if (r - l == 1 && arr[l] > arr[r]) {//两个元素,进行排序 swap(arr[l], arr[r]); } return ; } int mid = (l + r) >> 1; //开始分列 merge_sort(arr, l, mid);//递归左边数组 merge_sort(arr, mid + 1, r);//递归右边数组 int *temp = (int *)malloc(sizeof(int) * (r - l + 1));//创建一个空间,来存子数组的元素 int p1 = l, p2 = mid + 1, k = 0;//p1数组分裂开的前部分的起始坐标,p2数组分裂开后半部分的起始坐标 while (p1 <= mid || p2 <= r) { if (p2 > r || (p1 <= mid && arr[p1] < arr[p2])) temp[k++] = arr[p1++]; else temp[k++] = arr[p2++]; } memcpy(arr + l, temp, sizeof(int) * (r - l + 1));//将排好序的子数组拷贝给原数组 free(temp); return ; }4.基数排序:
这里假设数组都是两位数,先对数组进行元素的个位进行排序,然后在对数组的十位进行排序,这样就能对数组拍好序;如果位数不相同,取位数最大的数进行位数排序假如最大的位数是3位,那么就进行3次位数排序,如果位数10位那就进行10次位数排序;
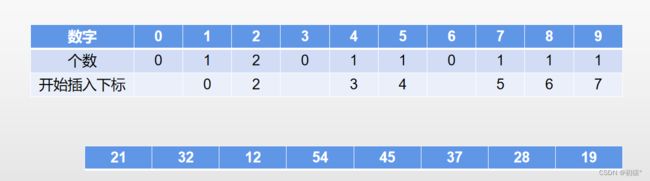
如图数组最初:
进行个位排序,上面的表格就是对于个位数的统计,对于排序时会起到作用:
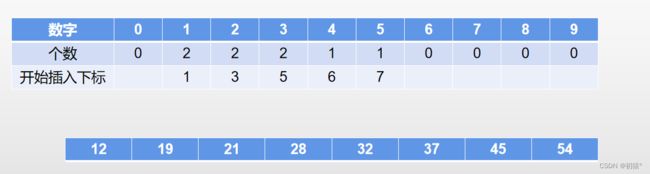
在进行10位排序:
最终完成排序:
时间复杂度:
代码实现:
void number_sort(int *arr, int n, int exp) { int count[10] = {0}; for (int i = 0; i < n; i++) { count[arr[i] / exp % 10] += 1;//对每位数的数的个数统计 } for (int i = 1; i < 10; i++) { count[i] += count[i - 1];//位数排序,从小到大,现在的操作就是使count变为下标 } int *sum = (int *)malloc(sizeof(int) * n); for (int i = n - 1; i >= 0; i--) {//假如个位已近排序后,那么个位大的在后,而根据十位排序也是从高位排到低位,所以需要倒过来存 sum[count[arr[i] / exp % 10] - 1] = arr[i];//下标从0开始,所以需要-1; count[arr[i] / exp % 10]--;//对应的位数已经排序一个,所以数量-1; } memcpy(arr, sum, sizeof(int) * n); free(sum); return ; } void radix_sort(int *arr, int n) { int max = INT_MIN; for (int i = 0; i < n; i++) {//获取最大数的数 max = max > arr[i] ? max : arr[i]; } for (int i = 1; max / i > 0; i *= 10) {//从个位一直到大于最大数的位数 number_sort(arr, n, i); } return ; }非稳定排序:
1.选择排序:
将数组分为两个区域一个已排序区和一个未排序区,每次将未排序区中的最值放在已排序区中;
这样一直在未排序区中选择,直到排序完成:
时间复杂度:
代码实现:
void select_sort(int *arr, int n) {//这里实现的是将最小的元素放在最前面,现在前面就是已排序区 for (int i = 0; i < n - 1; i++) { int ind = i;//ind先记录当前准备排序的位置 for (int j = i + 1; j < n; j++) { if (arr[ind] > arr[j]) ind = j;//ind记录未排序区中最小值的值的位置 } swap(arr[ind], arr[i]);//将未排序的区的最小值放在准备排序的位置 } return ; }2.快速排序:
选择数组头步位置,作为基数,用一个变量记录下来,然后将这个基数作为中间值,将数组分为两个部分,前半部分小于这个基数,后半部分大于基数,然后在对两个部分进行上面的操作,直接这两个部分不能再分;这里不一定是二分开的,有可能这个基数是最大值,那么就没有前半部分;
如图数组初始状态:
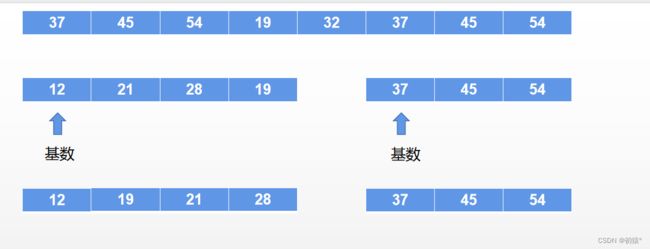
将32作为基数,把数组分为两部分分:
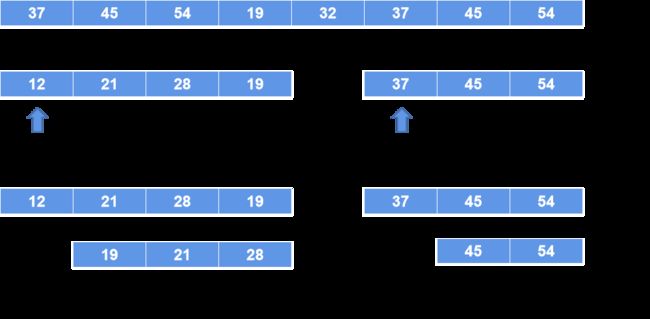
然后再对左边部分进行快排,右边部分进行快排
这里只是刚好,不用变化,然后继续上面的操作,直到最后排完序:
完成排序。
时间复杂度:
最坏:
代码实现:
//l最初为0,r最初为n-1 void quick_sort(int *arr, int l, int r) { if (r < l) return ; int x = l, y = r, num = arr[l]; while (x < y) { while (x < y && arr[y] >= num) y--;//如果大于基数的部分,该位置数大于基数就不用交换 if (x < y) arr[x++] = arr[y];//如果x3.希尔排序
希尔排序其实就是对于选择排序的一个优化的算法,而最最坏的情况就是降为一个普通的选择排序。
选择一个移动的长度,最开始选择数组长度的1/2,然后一直除2,直到步长等于1,进行一次插入排序;这个步长的作用就是,从一个位置往前移动多少步进行对该位置的值进行比较,如果不满住单调性就进行交换,然后交换如果还能往前目前的步长长度,继续往前比较;
如图,直接上图片理解:
现在的步长选作4,那么就从位置4进行开始排序:
他俩进行比较,然后数组是单调递增,就就需要交换,然后比较位置向后移动:
然后第一次步长结束后,那么步长在除以2:
然后再次进行比较
继续往后
这里发生了交换,而且现在的位置还能往前走步长,所以也需要比较:
比较后,不用发生交换,继续刚刚的位置往后:
直到不能发生交换,然后现在走到了最后的位置,进行步数除以2,等于1,进行一次选择排序:
这里发生了交换,那就需要再往前走步长那么长进行比较:
时间复杂度:

最坏:
代码实现:
void shell_sort(int *arr, int n) { int step; for (step = n / 2; step > 0; step >>= 1) {//步长循环 for (int i = step; i < n; i++) {//从步长长度开始往后循环 for (int j = i; j >= step && arr[j] < arr[j - step]; j -= step) { //如果不满足单调性,发生交换,并且如果现在的位置长度大于等于步长继续往前移动进行比较 swap(arr[j], arr[j - step]); } } } return ; }4.堆排序:
堆,堆排序在前面这个链接的文章里,因为单独将堆排序有那么一点难理解需要结合对堆的理解才容易一些;