408考研-数据结构算法-顺序表
数组
如何创建数组
我们以 Java 中创建数组为例,创建语法如下
dataType[] arrName = new dataType[size];
- dataType: 也就是我们数组中元素的数据类型
- arrName:即数组名
- size:即数组所能容纳的元素数量
- new: Java 语言中的关键词
假设我们要创建一个由 10 个元素的数组,其中元素的数据类型为 int,则创建的方法如下
int[] arr = new int[19];
顺序表采用顺序存储方式,即逻辑上相邻的数据在计算机内的存储位置也是相邻的。顺序存储方式,元素存储是连续的,中间不允许有空,可以快速定位第几个元素,但是插入和删除时需要移动大量元素。根据分配空间方法不同,顺序表可以分为静态分配和动态分配两种方法。
静态分配
顺序表最简单的方法是使用一个定长数组data[]存储数据,最大空间为Maxsize,用length记录实际的元素个数,即顺序表的长度。这种用定长数组存储的方法称为静态分配。
顺序表的静态分配结构体定义,如图2-3所示。采用静态分配方法,定长数组需要预先分配一段固定大小的连续空间,但是在运算的过程中,如合并、插入等操作,容易超过预分配的空间长度,出现溢出。解决静态分配的溢出问题,可以采用动态分配的方法。
动态分配
在程序运行过程中,根据需要动态分配一段连续的空间(大小为Maxsize),用elem记录该空间的基地址(首地址),用length记录实际的元素个数,即顺序表的长度。动态顺序表。采用动态存储方法,在运算过程中,如果发生溢出,可以另外开辟一块更大的存储空间,用以替换原来的存储空间,从而达到扩充存储空间的目的。

注意哦,这里有两个概念“数组的长度”和“线性表的长度”需要区分一下。
数组的长度是存放线性表的存储空间的长度,存储分配后这个量是一般是不变的。
线性表的长度是线性表中数据元素的个数,随着线性表插入和删除操作的进行,这个量是变化的。
在任意时刻,线性表的长度应该小于等于数组的长度。
数组基本操作
下面分别介绍数组的初始化、创建、取值、查找、插入、删除等基本操作。
1.初始化
初始化是指为顺序表分配一段预定义大小的连续空间,用elem记录这段空间的基地址,当前空间内没有任何数据元素,因此元素的实际个数为0。假设我们已经预定义了一个最大空间数Maxsize,那么就用new分配大小为Maxsize的空间,分配成功会返回空间的首地址,分配失败会返回空指针。
package com.maweiqi;
public class ArrayDemo {
public static void main(String[] args) {
int[] arr = new int[10];
int length = 0;
for (int i = 0;i< 5;i++) {
arr[length++] = i+1;
}
System.out.println("数组的容量:"+arr.length);
System.out.println("数组的长度:"+length);
}
}
创建数组
顺序表输入数据,输入数据的类型必须与类型定义中的类型一致。
算法步骤
1)初始化下标变量i=0,判断顺序表是否已满,如果是则结束;否则执行第2步。
2)输入一个数据元素x。
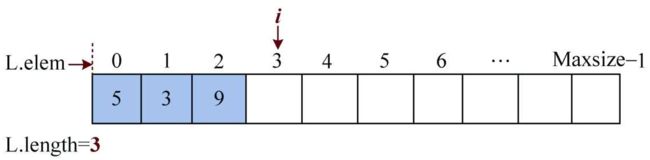
3)将数据x存入顺序表的第i个位置,即L.elem[i]=x,然后i++。
4)顺序表长度加1,即L.length++。
5)直到数据输入完毕。
1)输入元素:5。将数据元素5存入顺序表的第0个位置,即L.elem[0]=5,然后i++
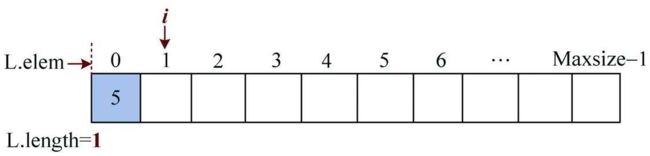
2)输入元素:3。将数据元素3存入顺序表的第1个位置,即L.elem[1]=3,然后i++
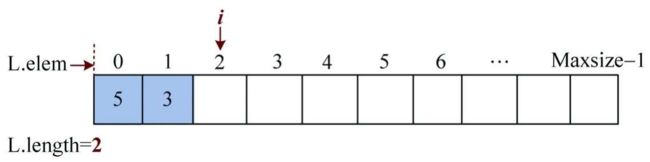
3)输入元素:9。将数据元素9存入顺序表的第2个位置,即L.elem[2]=9,然后i++
插入元素到数组
在顺序表中第i个位置之前插入一个元素e,需要从最后一个元素开始,后移一位……直到把第i个元素也后移一位,然后把e放入第i个位置
1)判断插入位置i是否合法(1≤i≤L.length+1),可以在第一个元素之前插入,也可以在第L.length+1个元素之前插入。
2)判断顺序表的存储空间是否已满。
3)将第L.length至第i个元素依次向后移动一个位置,空出第i个位置。
4)将要插入的新元素e放入第i个位置。
5)表长加1,插入成功返回true。
例:顺序表中的第5个位置之前插入一个元素9。
1)移动元素。从最后一个元素(下标为L.length-1)开始后移一位,移动元素过程如下,一共移动四位




2)插入元素。此时第5个位置空出来,将要插入的新元素9放入第5个位置,表长加1
要插入元素到数组中,可以分为如下3 中情况
1.插入数组开头
2.插入数组结尾
3.插入数组中间
package com.maweiqi;
import java.util.Arrays;
public class AddArrDemo {
/**
* 将元素插入到中间
*/
public static int[] insertMid(int[] arr ,int index,int val){
//创建一个新的数组,用于存放插入的元素
int[] destArr = new int[arr.length + 1];
//将原数组插入到元素位置前半段赋值给新数组
for (int i = 0; i< index; i++) {
destArr[i] = arr[i];
}
//将原数组插入到新数组的后半段
for (int j = index; j < arr.length; j++) {
destArr[j+1] = arr[j];
}
//将元素插入到新数组的指定位置
destArr[index] = val;
return destArr;
}
/**
* 插入元素到数组的结尾
*/
public static int[] insertEnd(int[] arr ,int val){
//创建一个新的数组,用于存放插入的元素
int[] destArr = new int[arr.length + 1];
//将元素插入到数组的结尾,同时将原数组整体复制到新数组
destArr[arr.length] = val;
for (int i = 0; i < arr.length; i++) {
destArr[i] = arr[i];
}
return destArr;
}
/**
* 插入元素到数组的开头
*/
public static int[] insertStart(int[] arr ,int val){
//创建一个新的数组,用于存放插入的元素
int[] destArr = new int[arr.length + 1];
//将元素插入到数组的开头,同时将原数组整体复制到新数组
destArr[0] = val;
for (int i = 0; i < arr.length; i++) {
destArr[i + 1] = arr[i];
}
return destArr;
}
public static void main(String[] args) {
int[] arr = new int[10];
for (int i = 0;i < arr.length; i++) {
if(i== 5){
break;
}
arr[i] = i+ 1;
}
// [1, 2, 3, 4, 5, 0, 0, 0, 0, 0]
// System.out.println(Arrays.toString(arr));
// int[] destArr01 = insertEnd(arr,11);
//[1, 2, 3, 4, 5, 0, 0, 0, 0, 0, 11]
// System.out.println(Arrays.toString(destArr01));
// int[] destArr02 = insertStart(arr,12);
//[12, 1, 2, 3, 4, 5, 0, 0, 0, 0, 0]
// System.out.println(Arrays.toString(destArr02));
int[] destArr03 = insertMid(arr, 3 , 13);
//[1, 2, 3, 13, 4, 5, 0, 0, 0, 0, 0]
System.out.println(Arrays.toString(destArr03));
}
}
删除数组中的元素
在顺序表中删除第i个元素,需要把该元素暂存到变量e中,然后从i+1个元素开始前移……直到把第n个元素也前移一位,即可完成删除操作
1)判断删除位置i是否合法(1≤i≤L.length)。
2)将欲删除的元素保存在e中。
3)将第i+1至第n个元素依次向前移动一个位置。
4)表长减1,删除成功,返回true。
删除第5个元素。
删除过程如下。
1)移动元素。首先将待删除元素2暂存到变量e中,以后可能有用,如果不暂存,将会被覆盖。然后从第6个元素开始前移一位,移动元素过程
2)表长减1,删除元素后的顺序表如图
同样的,假设我们要删除数组中的元素,也要考虑如下 3 种情况:
1.删除数组开头元素
2.删除数组末尾元素
3.删除数组中间元素
删除数组开头元素
删除开头元素,相当于将原数组开头元素后边的元素整体向前移动一位,而不用管开头的元素,
package com.maweiqi;
import java.util.Arrays;
public class DeleteArrDemo {
/**
*删除数组开头的元素
*/
public static int[]deleteStart(int[]arr){
//删除元素后,数组的容量减小
int[] destArr = new int[arr.length - 1];
//删除开头的元素,将后面的元素移动到前面
for (int i = 1;i < arr.length; i++) {
destArr[i - 1] = arr[i];
}
return destArr;
}
/**
*删除数组末尾的元素
*/
public static int[] deleteEnd(int[] arr){
//删除元素后,数组的容量减小
int[] destArr = new int[arr.length - 1];
//删除末尾的元素
for (int i = 0;i < arr.length - 1; i++){
destArr[i] = arr[i];
}
return destArr;
}
/**
*删除元素从中间开始删除
*/
public static int[] deleteMid(int[] arr,int index){
//删除元素后,数组的容量减小
int[] destArr = new int[arr.length - 1];
//删除指定位置元素,前半段保持
for (int i =0;i < index; i++) {
destArr[i] = arr[i];
}
//后半段整体向前移动一位
for (int j = index; j < arr.length - 1 ; j++) {
destArr[j] = arr[j + 1];
}
return destArr;
}
public static void main(String[] args) {
int[] arr = new int[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = i + 1;
}
// [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
System.out.println(Arrays.toString(arr));
//调用头部开始删除
// int[] ints = deleteStart(arr);
// [2, 3, 4, 5, 6, 7, 8, 9, 10]
// System.out.println(Arrays.toString(ints));
//调用从结尾删除数组元素
// int[] ints = deleteEnd(arr);
//[1, 2, 3, 4, 5, 6, 7, 8, 9]
// System.out.println(Arrays.toString(ints));
//删除中间元素
int[] ints1 = deleteMid(arr, 3);
// [1, 2, 3, 5, 6, 7, 8, 9, 10]
System.out.println(Arrays.toString(ints1));
}
}
修改数组元素
要修改数组元素,实际上只要知道需要修改数组元素的索引位置即可,然后将对应索引位置的值修改为你要修改的值即可
package com.maweiqi;
import java.util.Arrays;
public class UpdateArrDemo {
/**
* 修改数组任意位置元素
* @param arr 待修改元素的数组
* @param index 待修改元素索引位置
* @param val 修改后的元素值
* @return 修改元素后的数组
*/
public static int[] update(int[] arr,int index,int val){
arr[index] = val;
return arr;
}
public static void main(String[] args) {
int[] arr = new int[10];
for (int i = 0; i < arr.length; i++) {
arr[i] = i + 1;
}
// [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
System.out.println(Arrays.toString(arr));
//修改数组任意位置元素
int[] ints1 = update(arr, 3,100);
// [1, 2, 3, 5, 6, 7, 8, 9, 10]
System.out.println(Arrays.toString(ints1));
}
}
查找数组中的元素
要查找数组中的某一个元素,最常用的方法有如下两种
线性查找,主要针对数组较小时
二分查找,主要针对数组较大时,提高查询效率
线性查找
在顺序表中查找一个元素e,可以从第一个元素开始顺序查找,依次比较每一个元素值。如果相等,则返回元素位置(位序,即第几个元素);如果查找整个顺序表都没找到,则返回-1。例如,下图的顺序表中,查找元素8,查找到其下标为5,返回位序为6。
线性查找即遍历数组,然后判断各元素是否是目标值,是则输出对应索引位置,否则返回1,此时时间复杂度为O(n);
package com.maweiqi;
public class SearchArrDemo {
/**
*查找元素的方法
*/
public static int linearSearch(int[] array ,int target){
//查找到目标值时,返回目标索引
for (int i = 0; i < array.length; i++) {
if(target == array[i]){
return i;
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {2,3,5,7,8,11,15,18};
int index = linearSearch(arr,7) ;
// 返回的索引为:3
// 找到的值时:7
System.out.println("返回的索引为:"+index);
System.out.println("找到的值时:"+arr[index]);
}
}
二分查找
你小时候或许玩过这样一种猜谜游戏:我心里想着一个1到100之间的数字,在你猜出它之前,我会提示你的答案应该大一点还是小一点。
你应该凭直觉就知道这个游戏的策略。一开始你会先猜处于中间的50,而不是1。为什么?因为不管我接下来告诉你更大或是更小,你都能排除掉一半的错误答案!
如果你说50,然后我提示要再大一点,那么你应该会选75,以排除掉剩余数字的一半。如果在75之后我告诉你要小一点,你就会选62或63。总之,一直都猜中间值,就能不断地缩小一半的范围。
下面来演示这个过程,但仅以1到10为例。
有序数组相比常规数组的一大优势就是它除了可以用线性查找,还可以用二分查找。常规数组因为无序,所以不可能运用二分查找。
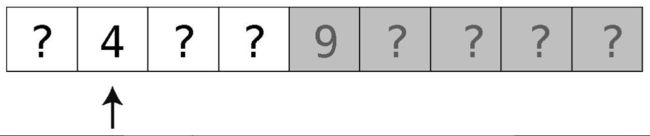
为了看出它的实际效果,假设有一个包含9个元素的有序数组。计算机不知道每个格子的值,如下图所示。
然后,用二分查找来找出7,过程如下。
第1步:检查正中间的格子。因为数组的长度是已知的,将长度除以2,我们就可以跳到确切的内存地址上,然后检查其值。
值为9,可推测出7应该在其左边的某个格子里。而且,这下我们也排除了一半的格子,即9右边的那些(以及9本身)。

第2步:检查9左边的那些格子的最中间那个。因为这里最中间有两个,我们就随便挑了左边的。
它的值为4,那么7就在它的右边了。由此4左边的格子也就排除了。
第3步:还剩两个格子里可能有7。我们随便挑个左边的。

第4步:就剩一个了。(如果还没有,那就说明这个有序数组里真的没有7。)

终于找到7了,总共4步。是的,这个有序数组要是用线性查找也会是4步,但稍后你就会见识到二分查找的强大。
当数组长度很小时,使用线性查找方法很快就能找到目标值是否存在并返回对应索引位置但当数组很大时,线性查找的方法效率就太低了。这时候二分查找是更理想的查找手段,二分查找实质是使用双指针,每次对半查找,大大提高效率,时间复杂度缩减为o(logn);
package com.maweiqi;
public class BinarySearchDemo {
//编写二分查找的方法
public static int binarySearch(int[] array ,int target){
//左指针和右指针
int left = 0;
int right = array.length - 1;
while (left <= right) {
//计算mid
int mid = left + (right - left) / 2;
//当前值等于目标值,直接返回目标的索引即可
if(array[mid] == target){
return mid;
}else if (array[mid] < target){
//当前值小于目标值,左指针向右移动一位
left = mid + 1;
}else {
//当前值大于目标值,,右指针向左移动一位
right = mid - 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {-1,2,3,5,7,11,18,21,33,56,78,98};
//2
// int index = binarySearch(arr,3);
//-1
int index = binarySearch(arr,13);
System.out.println(index);
}
}
顺序表的优点:操作简单,存储密度高,可以随机存取,只需要O(1)的时间就可以取出第i个元素。
顺序表的缺点:需要预先分配最大空间,最大空间数估计过大或过小会造成空间浪费或溢出。插入和删除操作需要移动大量元素。
在实际问题中,如果经常需要插入和删除操作,则顺序表的效率很低。为了克服该缺点,可以采用链式存储。
二分查找与线性查找区别
对于长度太小的有序数组,二分查找并不比线性查找好多少。但我们来看看更大的数组。
对于拥有100个值的数组来说,两种查找需要的最多步数如下所示。
❏ 线性查找:100步
❏ 二分查找:7步
用线性查找的话,如果要找的值在最后一个格子,或者比最后一格的值还大,那么就得查遍每个格子。有100个格子,就是100步。
二分查找则会在每次猜测后排除掉一半的元素。100个格子,在第一次猜测后,便排除了50个。
再换个角度来看,你就会发现一个规律。
长度为3的有序数组,二分查找所需的最多步数是2。
若长度翻倍,变成7(以奇数为例会方便选择正中间的格子,于是我们把长度翻倍后又增加了一个数),则最多步数会是3。
若再翻倍(并加1),变成15个元素,那么最多步数会是4。
规律就是,每次有序数组长度乘以2,二分查找所需的最多步数只会加1。这真是出奇地高效。
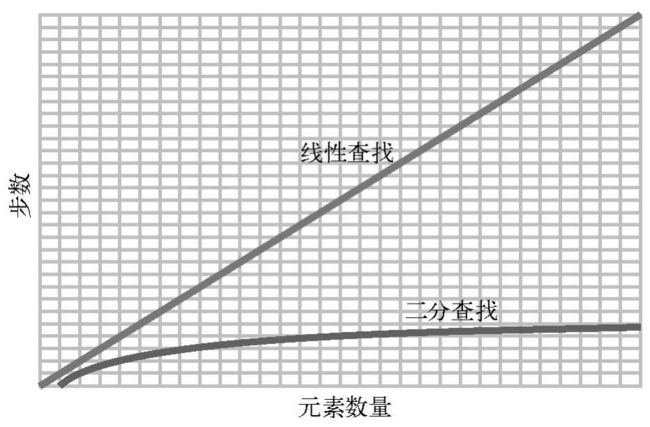
相反,在3个元素的数组上线性查找,最多要3步,7个元素就最多要7步,100个元素就最多要100步,即元素有多少,最多步数就是多少。数组长度翻倍,线性查找的最多步数就会翻倍,而二分查找则只是增加1步。
这种规律可以用下图来展示。
如果数组变得更大,比如说10000个元素,那么线性查找最多会有10000步,而二分查找最多只有14步。再增大到1000000个元素,则线性查找最多有1000000步,二分查找最多只有20步。
不过还要记住,有序数组并不是所有操作都比常规数组要快。如你所见,它的插入就相对要慢。衡量起来,虽然插入是慢了一些,但查找却快了许多。还是那句话,你得根据应用场景来判断哪种更合适。
总结
关于算法的内容就是这些。很多时候,计算一样东西并不只有一种方法,换种算法可能会极大地影响程序的性能。
同时你还应意识到,世界上并没有哪种适用于所有场景的数据结构或者算法。你不能因为有序数组能使用二分查找就永远只用有序数组。在经常插入而很少查找的情况下,显然插入迅速的常规数组会是更好的选择。
如之前所述,比较算法的方式就是比较各自的步数。