史上最细 B+Tree 解读
前言:
B+Tree 经过几十年的发展已经成为 OLTP 数据库的首选索引结构,深入分析开始前先介绍一些书籍给大家,B+Tree 的演进非常的复杂,有很多的大牛论文都做出了很关键的指导性作用,就算当前还是在不断探索优化的可能,其目的主要是为了降低锁粒度降低读写冲突。这里的锁可能不完全是大家以为的 Java 临界区线程锁,后面会详细阐述何为 Lock
有很多博文都有描述 Mysql 底层使用了 B+Tree 做索引,但是很多都很肤浅甚至看完后可能对这个数据结构的复杂性&重要性还是一无所知,希望这篇文章能让你重新认识 B+Tree
很多书籍、资料都是英文的,本文会全部使用中文来说明
推荐书籍:
下面这本书可以理解为 B+Tree 领域的圣经,对这种数据结构有兴趣或者想了解数据库底层到底是如何控制事务那么推荐看:Modern B-Tree Techniques
正文:
OLTP 为何亲睐B+ Tree:
要知道这个原因,那么需要先了解下什么是 LSM-Tree,为什么 OLAP 数据库会亲睐LSM-Tree。
LSM-Tree:
LSM Tree将存储数据切分为一系列的SSTable(Sorted String Table),一个SSTable内的数据是有序的任意字节组,而且SSTable一但写入磁盘中,就像日志一样不能再修改。当要修改现有数据时,LSM Tree并不直接修改旧数据,而是直接将新数据写入新的SSTable中。同样的,删除数据时,LSM Tree也不直接删除旧数据,而是写一个相应数据的删除标记的记录到一个新的SSTable中。这样一来,LSM Tree写数据时对磁盘的操作都是顺序块写入操作,而没有随机写操作。所以写入速度极高
SSTable:
LSM 的核心就是 SSTable,后续简称 SST,我们先来学习下什么是 SST
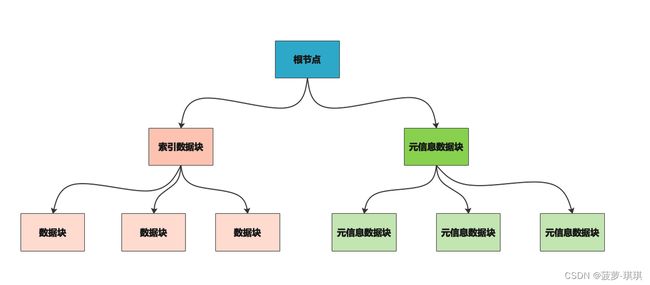
LevelDB/Hbase 等底层采用KV存储都使用了类似的思想,SSTable 文件的内容分为 5 个部分,根节点、索引块、元信息块、过滤块和 数据块。
相对有序性:
为了加速分段合并的效率,SST 每一段都确保了key 的有序性,其实是通过在内存中使用平衡树(红黑树)来做的,先在内存中使用红黑树排序,然后在将新的数据刷到磁盘中,但是这样做会有一个风险点就是数据丢失,后来为了规避这个问题有加入 WAL 日志,和大多数中间件解决方案差不多通过 WAL 预写日志来解决突然崩溃导致的数据丢失风险也提高了写入速度
过滤块:
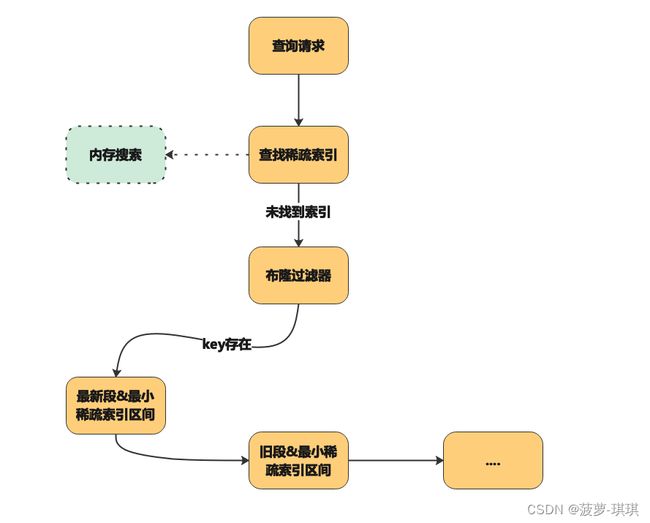
这部分主要采用布隆过滤器来做的实现,原因很简单如果查询一个不存在的数据,那么 SST 会先查找索引发现不在索引块,那么就会从数据块中开始二分查找,最终全部扫完后才发现数据不存在,这是一种极其低效的过程
位图里面存储的就是已存在的数据指纹
分段稀疏索引:
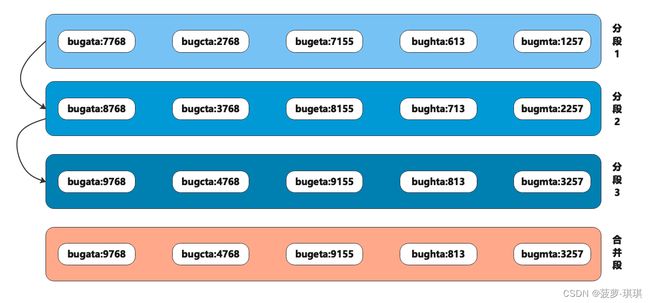
SST 写入速度较快,因为没有复杂的读写锁等问题,数据的写入采用分段追加方式,并且每一段的 key 是有序的不会有重复数据,这样在多段数据合并的时候逻辑就比较简单高效。多个段出现重复 key 数据的时候直接保留最新段丢弃老段数据即可
如果每一个数据 key 都放到内存做索引显然需要很大的内存开销并且可能很多 key 几乎很少被使用,所以 SST 采取了一种稀疏索引分段存储方式
可以看到底层存储时每一段的索引是跳跃连续的,这样在分段1查找 bugbta 时,虽然没有这个索引,但是有 bugata 的索引,所以直接调到 bugata 且直接越过7768个字节(7768代表的是 bugata 这个索引的值长度)继续往后扫描,很快可以扫描到 bugbta 的所在位置,这样就保证了内存合理使用以及性能的折中方案。
多段合并:
上面可以看到段1、段2、段3在合并后形成了新的合并段数据,这里的合并逻辑相对简单,因为每一段在写入时就确保了字符顺序是有序且唯一的,所以在合并的时候发现有重复 key 只需要保留新版本丢弃旧版本即可
查询过程:
OLTP 不适用:
不知道小伙伴们有没有发现为什么OLTP 数据库不适用 LSM 结构嘛?因为数据写入、更新、删除全部都是追加写,仔细想想如果需要支持事务的特性应该怎么实现呢?
我的理解是太难了!!!如果熟悉 B+Tree 对事务实现熟悉的小伙伴,那么就会了解 LSM 实现事务特性有多复杂。但是也正应如此,OLAP 数据库才会很适用 LSM 结构,因为不需要考虑事务特性,并且大多 OLAP 场景都是有着很高的写入 TPS 要求(实时数仓),由于数据变更操作都不会立即触发加锁&变更&释放锁过程,而是追加写所以 LSM 天然能够支持很高的 TPS,按照星云使用的 HBASE 来看,可以支持8W+的 TPS同时保证6W+的 QPS,并且 P99 RT 稳定
B+ Tree :
简介:
文献摘录于:维基百科《B 树》
在B(+)树,这些键值的拷贝被存储在内部节点;键值和记录存储在叶子节点;另外,一个叶子节点可以包含一个指针,指向另一个叶子节点以加速顺序存取。
B*树分支出更多的内部邻居节点以保持内部节点更密集地填充。此变体要求非根节点至少2/3填充,而不是1/2。为了维持这样的结构,当一个节点填满之后将不会再立即分割节点,而是将它的键值与下一个节点共享。当两个节点都填满之后,分割成3个节点。
计数B树存储,每一树都带有一个指针和其指向子树的节点数目。这就允许了以键值为序快速查找第N笔记录,或是统计2笔记录之间的记录数目,还有其他很多相关的操作。
在B树中,内部(非叶子)节点可以拥有可变数量的子节点(数量范围预先定义好)。当数据被插入或从一个节点中移除,它的子节点数量发生变化。为了维持在预先设定的数量范围内,内部节点可能会被合并或者分离。因为子节点数量有一定的允许范围,所以B树不需要像其他自平衡查找树那样频繁地重新保持平衡,但是由于节点没有被完全填充,可能浪费了一些空间。子节点数量的上界和下界依特定的实现而设置。例如,在一个2-3 B树(通常简称2-3树),每一个内部节点只能有2或3个子节点。 B树中每一个内部节点会包含一定数量的键,键将节点的子树分开。例如,如果一个内部节点有3个子节点(子树),那么它就必须有两个键: a(1) 和 a(2) 。左边子树的所有值都必须小于 a(1) ,中间子树的所有值都必须在 a(1) 和a(2) 之间,右边子树的所有值都必须大于 a(2) 。
结构:
B-Tree 1970年出现,时至今日几乎成为了关系型数据库中标准索引实现方案,很多非关系型数据库也在使用。
和 SST 一样,B-Tree 也保留了按键排序的特性,这样可以实现高效的范围查询,B-Tree 将数据库分解成了固定大小的块/页,一般大小为4KB,页是内部读写的最小单元。这样设计是为了更加契合底层的硬件,磁盘也是以固定大小的块排列的
为了节省时间,我就不详细分析 B-Tree 了,主要以 B+ Tree 入手,其实 B*就是普通 B 树的一种优化,为了操作简化以及操作效率出现的一种产物,所以有句话一直说所有科学的进步都是为了让人类偷懒...
简单看下区别吧:
| B树 | B+树 |
| 数据存储在叶节点和内部节点中 | 数据仅存储在叶节点中 |
| 查找、插入、删除等操作相对较慢 | 查找、插入、删除等操作相对较快 |
| 不存在多余的搜索键 | 可能存在冗余密钥 |
| 叶节点不链接在一起 | 叶节点作为链表链接在一起 |
| 与 B+ 树相比,它们没有优势,因此,它们不在 DBMS 中使用 | 与 B 树相比,它们具有优势,因此,由于其效率,它们在 DBMS 中得到应用 |
存储:
某一页被指定为 B*的根,每当查找索引中一个 Key 时,就从这里开始向下搜索,该页包含了若干个键和对子页的引用,B*核心就是多级索引使用
数据透视:
-
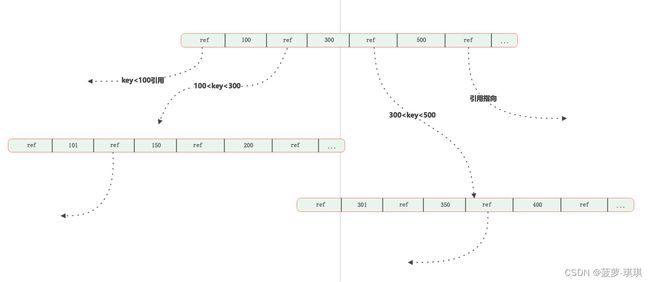
每个内部节点key 是有序且稀疏的,这点和 SST 差不多
-
稀疏 key 的中间会有一个指向其他内部节点的引用,主要为了加速查找
插入新数据:
-
先找到键添加应该所属页,这个时候就会有2种情况
-
原先页空间不够
-
涉及到页的分裂
-
-
原先页空间足够
-
-
维持树相对平衡
-
在叶子结点进行值存储
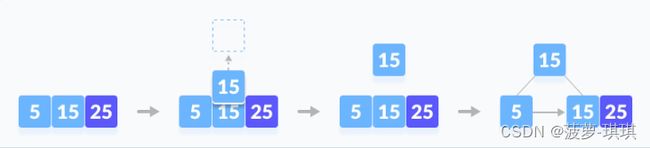
原始数据5&15
插入新数据25
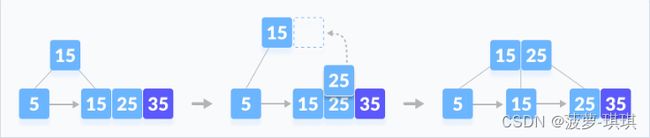
插入新数据35
整个过程可以看到是会保持树的相对平衡,然后不断分裂、分裂在分裂过程,分裂过程中也同时会保持节点的有序&稀疏特性。
上面解释的是数据结构的变化,但是写入过程还有其他操作,因为涉及到页的分裂&覆盖原页等操作,为了避免崩溃带来的风险,也会有 WAL 流程(重做日志)
删除数据:
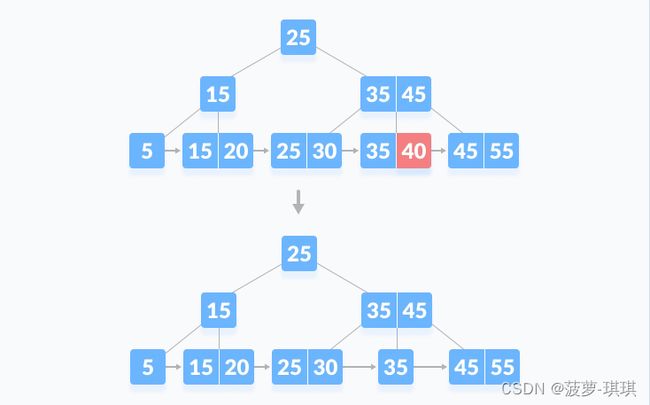
删除key=40数据,不涉及到重平衡
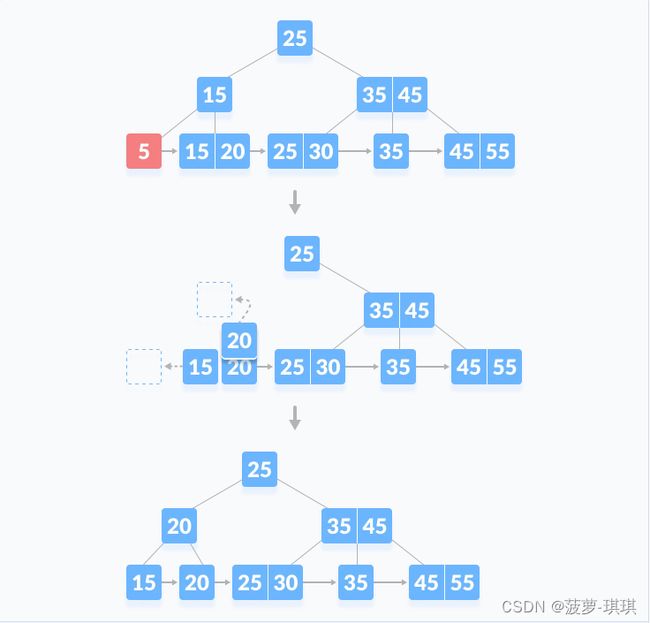
删除key=5数据,涉及到重平衡,借用兄弟节点的元素进行重平衡
优化内存占用:
目前示例中看到的 key 索引数据都是可读数值,在实际保存时会对索引进行压缩存储,只保留索引的缩略信息,这样可以确保一页中保留更多的 key 数据,降低树的层数
事务实现:
之前有提到过LSM 不适合事务场景,B*适合事务场景,我们现在开始详细了解下 B*是怎么满足事务特性对接节点Lock 的。
并发控制一直是数据库领域研究的热点和工程实现中的重点和难点。简单的说,就是要实现:并行执行的事务可以满足某一隔离性级别的正确性要求。要满足正确性要求就一定需要对事务的操作做冲突检测,对有冲突的事务进行延后或者丢弃。根据检测冲突的时机不同可以简单分成三类:
-
在操作甚至是事务开始之前就检测冲突的基于Lock的方式;
-
在操作真正写数据的时候检测的基于Timestamp的方式;
-
在事务Commit时才检测的基于Validation的方式。
数据库基本都采用乐观锁,越乐观认为发生冲突的概率越低,越倾向推迟冲突的检测这样可以获得更高的并发,但当冲突真正出现时,由于前面的操作可能都需要一笔勾销,因此在冲突较多的场景下,太乐观反而得不偿失。
并发控制中的Lock跟我们在多线程编程中保护临界区的Lock不是一个东西, Lock通常有不同的Mode,如常见的读锁SL,写锁WL,不同Mode的锁相互直接的兼容性可以用兼容性表来表示。
多个事务可以同时持有SL,但已经有WL的元素不能再授予任何事务SL或WL。这点其实和 java 的读写锁是一个逻辑,数据库通常会有一个调度模块来负责资源的加锁放锁,以及对应事务的等待或丢弃。所有的锁的持有和等待信息会记录在一张Lock Table中,调度模块结合当前的Lock Table中的状况和锁模式的兼容表来作出决策。
历代Lock 实现:
2PL:
这个时期的加锁策略认为树节点是最小的加锁单位。由于B+Tree的从根向下的搜索模式,事务需要持有从根节点到叶子节点路径上所有的锁。而两阶段锁(2PL)又要求所有这些锁都持有到事务Commit。更糟糕的是,任何插入和删除操作都有可能导致树节点的分裂或合并(Structure Modification Operations, SMO),因此,对根结点需要加写锁WL,也就是说任何时刻只允许一个包含Insert或Delete操作的事务进行。显而易见,这会严重的影响访问的并发度。
3PL:
针对这个问题,3PL应运而生,他正是利用B+Tree这种从根访问的特性,实现在放松2PL限制,允许部分提前放锁的前提下,仍然能够保证Serializable:
-
先对root加锁
-
之后对下一层节点加锁必须持有其父节点的锁
-
任何时候可以放锁
-
对任何元素在放锁后不能再次加锁
这种加锁方式也被称为Lock Coupling。直观的理解:虽然有提前放锁,但自root开始的访问顺序保证了对任何节点,事务的加锁顺序是一致的,因此仍然保证Seralizable。3PL实现上需要考虑一个棘手的问题:就是对B+Tree而言,一直要搜索到叶子结点才可以判断是否发生SMO。以一个Insert操作为例,悲观的方式,对遇到的每一个节点先加写锁,直到遇到一个确认Safe的节点(不会发生SMO);而乐观的方式认为SMO的相对并不是一个高频操作,因此只需要先对遇到的每个节点加读锁,直到发现叶子节点需要做分裂,才把整个搜索路径上所有的读锁升级写锁(Upgrade Lock)。当两个持有同一个节点读锁的事务同时想要升级写锁时,就会发生死锁,为了避免这种情况,引入了Update Lock Mode,只有Update Lock允许升级,并且Update Lock之间不兼容,这其实是一种权衡。
Blink Tree:
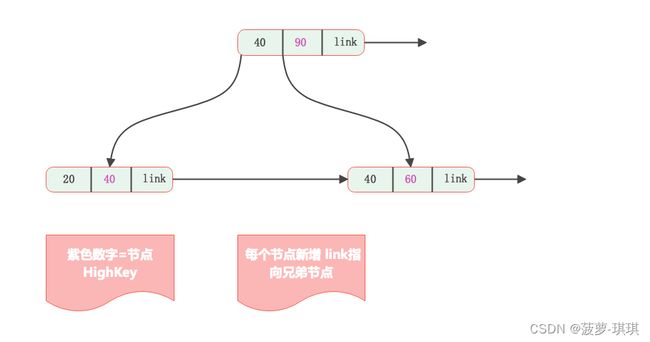
仔细分析会发现,2PL和3PL中面临的最大问题其实在于:节点的SMO时需要持有其父节点的写锁。正因为如此才不得不在搜索过程提前对所有节点加写锁,或者当发现SMO后再进行升级,进退维谷。而之所以这样,是由于需要处理父节点中的对应key及指针,节点的分裂或合并,跟其父节点的修改是一个完整的过程,不允许任何其他事务看到这个过程的中间状态。针对这个问题,Blink Tree巧妙的提出对所有节点增加右向指针,指向其兄弟节点,这是个非常漂亮的解决方案,因为他其实是提供了一种新的节点访问路径,让上述这种SMO的中间状态,变成一种合法的状态,从而避免了SMO过程持有父节点的写锁。
-
在每个节点(包括内部节点和叶子节点)中,键以递增顺序排列。
-
内部节点还存储了称为“高键(high key)”的数据,这个数据用于存储本节点中最大键的数据。
-
同层的兄弟节点之间,以“指针”相连接。
HighKey 引入的作用:
进行 SMO 的时候不再需要持有父节点锁,获取更大并发的可能!!!下面是一段白话文来描述为什么不再需要持有父节点的锁
向树中插入数据v:
初始化保存路径上经过节点的栈
// 第一部分:内部节点的遍历
如果当前的节点还是内部节点:
加载节点t到内存中
将当前节点t保存到栈中
查找路径上的下一个内部节点
// 到了这里意味着到了叶子节点这一层// 第二部分:在叶子节点上遍历找到数据所在的叶子节点
对上一步最后的内部节点加锁
在叶子节点所在的层逐步向右遍历找到节点所在的叶子节点,流程如下:
如果当前节点不是v所在的叶子节点,且不为空节点:
加锁当前节点
释放上一个被锁住的节点
将当前节点读入内存中
// 到了这里意味着找到了所在的叶子节点,下面进行插入操作// 第三部分:修改所在的叶子节点插入数据
修改所在的叶子节点A插入数据:
如果叶子节点A是安全(safe)节点:
插入数据
解锁叶子节点A
返回
否则如果是不安全(unsafe)的节点:
插入操作时不安全意味着就要进行split操作
分配新页面用于保存split后的新页面B'
插入的数据v写入节点A',需要split出去的数据写入节点B'
y为split后的A'的high key
写入B
写入A,同时修改父节点对应节点A的key为y
从栈中弹出上一个层次的节点,继续回溯做可能的平衡节点操作
解锁当前节点
说白了就Link 约等于 指针的作用,所以父节点的锁不再需要持有,而是在SMO 全部成功结束后替换涉及到的节点中的 link 指向就变成了原子操作
思考时间:
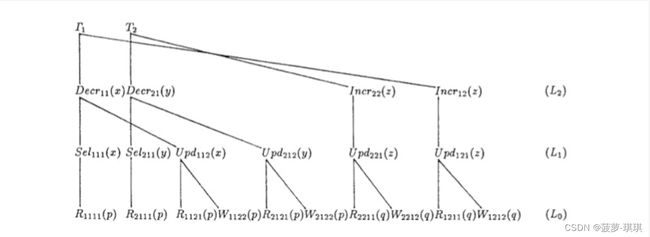
2PL - 3PL - Blink 所有焦点都是对着锁的粒度,到 Blink 时代后粒度已经变成了单页进行 Lock,能不能更进一步提升Btree的并发能力呢?《Principles and realization strategies of multilevel transaction management》对这个问题进行了深入的研究,下图来源于网络中
简单来描述这个图的意思就是分层事务思想,如果能在L1层,也就是对Record而不是Page加锁,就可以避免T1和T2在Page p Lock上的等待,如上图所示,T1和T2对Record x和Record y的操作其实是并发执行的。而L0层对Page的并发访问控制可以看做是上层事务的一个子事务或嵌套事务,其锁持有不需要持续整个最外层事务的生命周期
ARIESKVL:
《ARIESIKVL: A Key-Value Locking Method for Concurrency Control of Multiaction Transactions Operating on B-Tree Indexes》出了一套完整的、高并发的实现算法,引导了B+Tree加锁这个领域今后几十年的研究和工业实现。
ARIESKVL首先明确的区分了B+Tree的物理内容和逻辑内容,逻辑内容就是存储在B+Tree上的那些数据记录,而B+Tree自己本身的结构属于物理内容,物理内容其实事务是不关心的,那么节点分裂、合并这些操作其实只是改变了B+Tree的物理内容而不是逻辑内容。因此,ARIES/KVL就将这些从Lock的保护中抽离出来,也就是Lock在Record上加锁,对物理结构则通过Latch来保护其在多线程下的安全。这里最本质的区别是Latch不需要在整个事务生命周期持有,而是只在临界区代码的前后,这其实也可以看作上面分层事务的一种实现
物理结构&Latch锁:
Latch就是我们在多线程编程中熟悉的,保护临界区访问的锁。通过Latch来保护B+Tree物理结构其实也属于多线程编程的范畴,其作用对象也从事务之间变成线程之间。比如Lock Coupling变成了Latch Coupling;比如对中间结点先持有Read Latch或Update Latch,而不是Write Latch,等需要时再升级;又比如,可以采用Blink的方式可以避免SMO操作持有父节点Latch。以及这个方向后续的一些无锁结构如BW-Tree,其实都是在尝试进一步降低Latch对线程并发的影响。
逻辑结构&Lock锁:
有了这种清晰的区分,事务的并发控制就变得清晰很多,不再需考虑树本身的结构变化。假设事务T1要查询、修改、删除或插入一个Record X,而Record X所在的Page为q,那么加Lock过程就变成这样:
Search(X)and Hold Latch(q);
SLock(X) or WLock(X);
// Fetch, Insert or Delete
Unlatch(q);
RangeLock 锁:
很多数据库访问并不是针对某一条记录的,而是基于条件的。比如查询满足某个条件的所有Record,这个时候就比较麻烦了,按照上面的流程只能满足一个record 加锁,如果是范围那么又会回到在搜索满足数据的过程中进行全锁过程。
幻读:
范围查询最麻烦的就是解决幻读,事务的生命周期中,由于新的满足条件的Record被其他事务插入或删除,导致该事务前后两次条件查询的结果不同
Gap 锁:
对record 数据的前后间隙进行加锁,扫描到符合条件的 key 加锁后,在这些 key 的前后间隙也加上锁,这样就能确保不会出现幻读
那么我们有没有想过有这种情况:
-
扫描到的 key 正好是最大值
-
扫描到的 key 正好是最小值
这两种场景加 Gap 锁的时候就会出现锁之前/之后的无穷大,这种方式显然是无法接受的,后续又再次进行了 Gap 锁的优化
Instant Locking:
Instant Locking只在瞬间持有这把Next Key Locking,其加锁是为了判断有没有这个Range冲突的读操作,但获得锁后并不持有,而是直接放锁。乍一看,这样违背了2PL的限制,使得其他事务可能在这个过程获得这把锁。通过巧妙的利用Btree操作的特性,以及Latch及Lock的配合,可以相对完美的解决这个问题,如下是引入Instant Locking后的Insert加Next Key Lock的流程:
Search(M,Y)and Hold Latch(q);
XLock(Y);
Unlock(Y)
XLock(M);
Insert M into q
Unlatch(q);可以看出,Y上Lock的获取和释放,和插入新的Record两件事情是在Page q的Latch保护下进行的,因此这个中间过程是不会有其他事务进来的,等Latch释放的时候,新的Record其实已经插入。
Ghost Records:
Ghost Record的思路,其实跟之前讲到拆分物理内容和逻辑内容是一脉相承的,Ghost Record给每个记录增加了一位Ghost Bit位,正常记录为0,当需要删除某个Record的时候,直接将其Ghost Bit修改为1即可,正常的查询会检查Ghost Bit,如果发现是1则跳过。但是Ghost Record是可以跟正常的Record一样作为Key Range Lock的加锁对象的。可以看出这相当于把删除操作变成了更新操作,因此删除事务不再需要持有Next Key Lock。除此之外,由于回滚的也变成了修改Ghost Bit,不存在新的空间申请需要,因此避免了事务回滚的失败。Ghost Record的策略也成为大多数B+Tree数据库的必选实现方式。