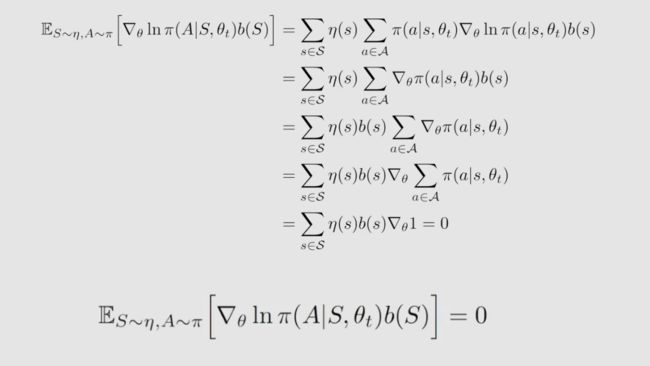强化学习:Actor-Critic (AC)算法
Actor-Critic是现在强化学习当中最流行的方法之一,它和 policy gradient 实际上是一种方法,只是它把基于value 的方法引入到policy gradient 当中。那么,actor-critic 当中 actor 和 critic 分别代表什么意思呢? actor 指的是策略更新,因为策略用于每个状态选取行为。 critic 指的是策略评估或价值评估,因为它通过评估策略或价值来判断当前策略的好坏。
QAC 算法
QAC 算法是最简单的 actor-critic 的算法。actor-critic 本身是 policy gradient,所以在介绍 QAC 算法之前,我们先回顾一下 policy gradient 。policy gradient 的基本思路是首先要有一个目标函数 可以是 v ˉ π \bar v_π vˉπ 也可以是 r ˉ π \bar r_π rˉπ ;第二步有目标函数就对其进行优化,通过采样的方法将含有求期望 E E E 的算法转化成一个不含有求期望 E E E ,如下:

从这个算法中我们可以知道 actor 和 critic ,这个算法对应的就是 Actor ,因为这个算法在不断更新策略的参数 θ \theta θ ,也就是在更新策略;而估计 q t ( s , a ) q_t(s,a) qt(s,a) 的算法就相当于critic 。
其中,用 MC 算法 估计 q t ( s , a ) q_t(s,a) qt(s,a) 的算法叫 reinforce 算法;用 DT 算法 估计 q t ( s , a ) q_t(s,a) qt(s,a) 的方法叫 Actor-Critic (AC)算法。QAC 算法是最简单的 actor-critic 的算法。其伪代码如下:

QAC 算法 的目标是去优化目标函数 J ( θ ) J(θ) J(θ) 。在第 t t t 步,假设当前的状态是 s t s_t st 当前的策略是对应的参数是向量 θ t θ_t θt 。然后根据 策略生成一个 action a t a_t at 和环境进行交互得到 r t + 1 r_{t+1} rt+1 和 s t + 1 s_{t+1} st+1 ,到了状态 s t + 1 s_{t+1} st+1 再根据其对应的策略得到一个新的 a t + 1 a_{t+1} at+1 。就有了 s t , a t , r t + 1 , s t + 1 , a t + 1 s_t,a_t, r_{t+1}, s_{t+1},a_{t+1} st,at,rt+1,st+1,at+1 这 5 个量,这 5 个量实际上就是一个 experience sample,接下来要做的是 critic (value update) ,就是把这些参数放到 Sarsa+值函数近似 算法当中去估计 action value q q q。把这个 q q q 代到 actor 中,得到一个新的策略后就会用到下一步去生成新的数据。
.
Advantage actor-critic 算法 (A2C)
A2C 实际上是 QAC 的一个推广,它基本的思想是在 QAC 当中我引入一个偏置量来减少估计方差。如下:


在介绍 A2C 算法之前,我们来介绍一个性质:策略梯度 policy gradient 引入一个新的偏置是不会发生变化的。
为什么要引入一个新的偏置 b b b ,它究竟有什么用?期望 E ( X ) E(X) E(X) 与 b ( s ) b(s) b(s) 无关,但方差 var ( X ) (X) (X) 与 b ( s ) b(s) b(s) 有关。如果 X X X 是标量,方差公式如下:

如果 X X X 是向量量,那么它的方差为一个矩阵,通常用其对角线元素的和来表示方差大小,公式如下:
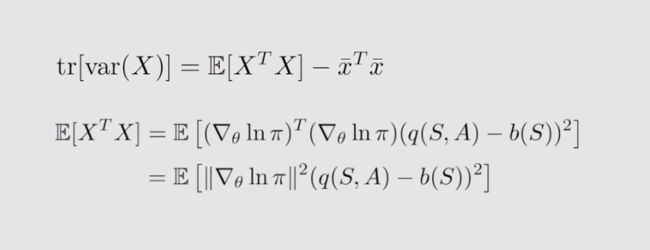
我们知道 方差 var(X) 与 b ( s ) b(s) b(s) ,那么我们就可以选择一个最优的 b ( s ) b(s) b(s) 来最小化方差 var(X) ,因为方差越小说明采样误差越小。理论上最优的 b ( s ) b(s) b(s) 如下:
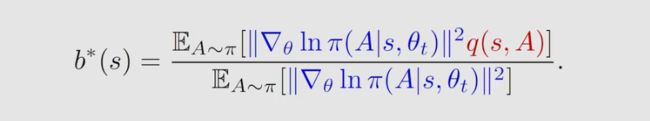
但在实际中我们并不会使用,因为其计算复杂,我们通常是去掉权重 ∣ ∣ [ ▽ θ l n π ( A ∣ s , θ t ) ∣ ∣ 2 ||[▽_\theta lnπ(A|s,\theta _t)||^2 ∣∣[▽θlnπ(A∣s,θt)∣∣2 得到 b ( s ) b(s) b(s) 就等于 v π ( s ) v_π(s) vπ(s) , 如下式子:

.
现在,我们就可以正式来介绍 A2C 算法了。当 b ( s ) = v π ( s ) b(s)=v_π(s) b(s)=vπ(s) 时,有:
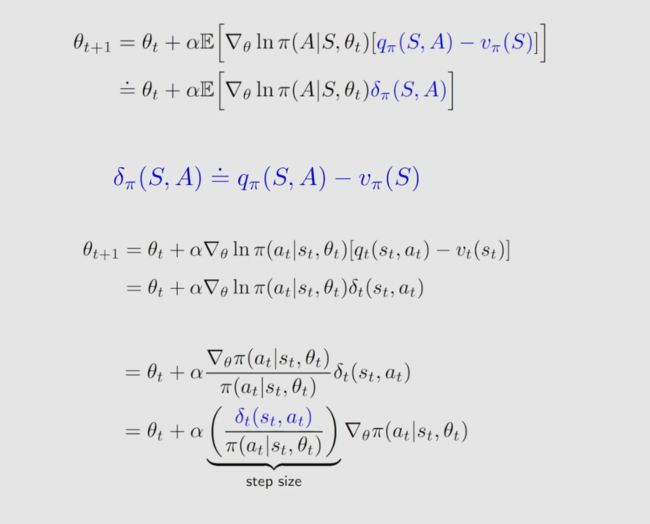
我们还可以做进一步的替换,发现 Advantage 函数可以用 TD error 来近似,这样替换的好处是只需要用一个神经网络来计算 v ( s ) v(s) v(s) 而不需要再使用一个神经网络去计算 q ( s , a ) q(s,a) q(s,a),如下:

可以替换,这是因为:
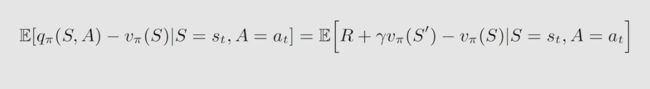
A2C 伪代码如下:

在第 t t t 时刻,根据当前的策略来得到一个 a t a_t at 和环境进行交互得到 r t + 1 r_{t+1} rt+1 和 s t + 1 s_{t+1} st+1 ,再来计算 TD error ,然后把这个 TD error 带入到这个 critic 当中得到 δ t δ_t δt 再将其带入到 actor 中得到 θ t \theta _t θt 更新策略。
Off-policy actor-critic
之前学的 策略梯度法和AC都是 on-policy ,如果之前有一些经验了,现在想用这些经验该怎么办呢?我们可以用off-policy 的 actor-critic 的方法。我们可以用 重要性采样 将AC 从 on-policy 转成 off-policy 。
怎么通过一些样本求出 期望 E E E 呢?第一种方法是我们可以直接用 MC 算法:

在介绍第二种方法之前,我们来考虑这样一个问题:能不能用服从概率分布 P 1 P_1 P1 采得的样本去估计服从概率分布为 P 0 P_0 P0 的期望 E E E 呢?为什么我们要这么问呢?因为我们要做 off-policy ,而 off-policy 有一个behavior policy β \beta β ,还有一个 target policy π π π ,而我要用服从 β \beta β 分布采样的数据去估计在 π π π 分布下的 E E E 。直接求肯定是不行的,这里我们要是有 重要性采样。
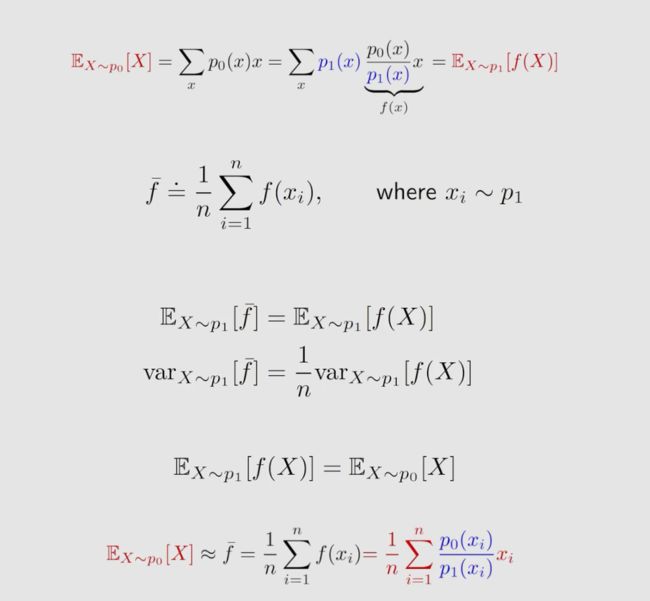
p 0 ( x i ) p 1 ( x i ) {p_0(x_i) \over p_1(x_i)} p1(xi)p0(xi) 称为重要性权重。
如果 p 0 ( x i ) = p 1 ( x i ) {p_0(x_i) =p_1(x_i)} p0(xi)=p1(xi) ,则重要性权重为 1, f ˉ \bar f fˉ变为 x ˉ \bar x xˉ。
如果 p 0 ( x i ) ≥ p 1 ( x i ) {p_0(x_i)≥p_1(x_i)} p0(xi)≥p1(xi) ,那么重要性权重 >1
现在,我们将重要性采样应用到 policy gradient 中去实现 off-policy 。有两个步骤,第一步就是要得到 gradient 的表达式;第二步将表达式应用梯度上升方法进行优化
假设,有一个behavior policy β \beta β 用来生成经验样本;我们的目标是优化 目标函数 J ( θ ) J(\theta) J(θ) , θ \theta θ 是 target policy π π π 的参数。 d β ( S ) d_β(S) dβ(S) 是在策略 β β β 下面的一个固定分布, v π ( s ) v_π(s) vπ(s) 是在策略 π π π 下所对应的 state Value。

其梯度表达式如下:

优化如下:

.
Deterministic actor-critic (DPG)
到目前为止,策略梯度方法中使用的策略对每一个 ( s , a ) (s,a) (s,a) 都要求 π ( a ∣ s , 0 ) ∈ [ 0 , 1 ] π_(a|s,0)∈[0,1] π(a∣s,0)∈[0,1] ,现在我们在策略梯度方法中使用确定性策略,如下:

μ μ μ是从 S 到 A S到A S到A 的映射函数,参数为 θ \theta θ 输入 s s s 输出 a a a ,我们有时简写为 μ ( s ) μ(s) μ(s)。
同样,有两个步骤,第一步就是要得到 gradient 的表达式;第二步将表达式应用梯度上升方法进行优化

我们选择 d 0 d_0 d0 独立于 μ μ μ,这种情况下的梯度容易计算。这里有两种选择 d 0 d_0 d0 的特殊但重要的情况。一是 d 0 ( s 0 ) = 1 和 d 0 ( s ≠ s 0 ) = 0 d_0(s_0)=1 和 d_0(s≠s_0)=0 d0(s0)=1和d0(s=s0)=0,其中 d 0 ( s 0 ) d_0(s_0) d0(s0) 是一种特定的启动状态。二是 d 0 d_0 d0 是 a a a 的平稳分布且与 μ μ μ 是不同的行为策略。