《经典递归问题：汉罗塔》

作者：@TheMythWS.

专栏：《JavaSE》

座右铭：不走心的努力都是在敷衍自己，让自己所做的选择，熠熠发光。

目录

✨汉罗塔的介绍

图解游戏​

✨N层汉罗塔需移动的次数

✨汉罗塔的代码实现 

c语言实现：

运行结果：

 java语言实现：

运行结果：

---

✨汉罗塔的介绍

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

图解游戏

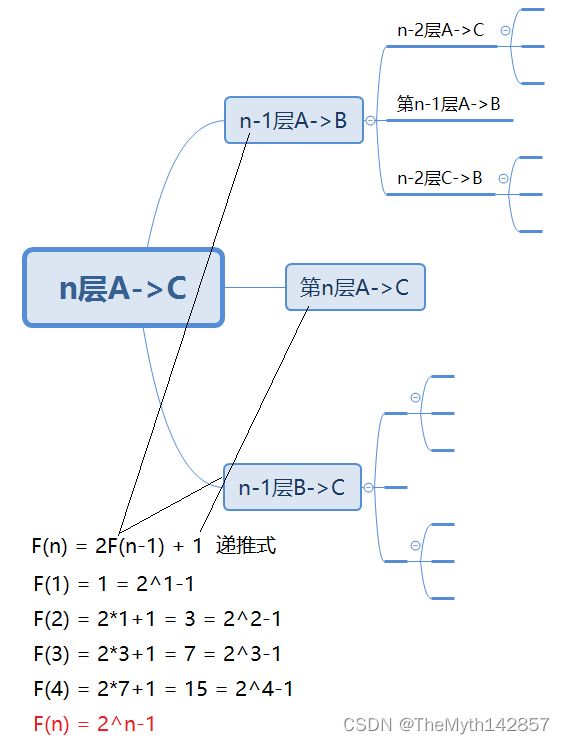
✨N层汉罗塔需移动的次数

✨汉罗塔的代码实现 

c语言实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include
/*
思路1：
 *      将1~N层从A->B，     A为源，B为目的，C作为辅助 角色在变化
 *      等价于
 *      1、把1~1-N层从A->C，A为源，B为辅助，C为目的
 *      2、把第N层从A->B
 *      3、把1~N-1层从C->B，A为辅助，B为目的，C为源
思路2：
 *      将1~N层从A->C，     A为源，B作为辅助，C为目的 角色在变化
 *      等价于
 *      1、把1~1-N层从A->B，A为源，B为目的，C为辅助
 *      2、把第N层从A->C
 *      3、把1~N-1层从B->C，A为辅助，B作为源，C作为目的
*/
/*
  将N个盘子从source移动到target的路径的打印
  N      初始的N个从小到大的盘子，N是最大编号
  from   原始柱子
  to     目标柱子
  help   辅助的主子
 */
//思路1
void printHannoiTower1(int n, char from[], char to[], char help[]) {//将1~N层从A->B，     A为源，B为目的，C作为辅助 角色在变化
	if (n == 1) {
		printf("move %d from %s to %s\n", n, from, to);//把第N层从A->B
		return;
	}
	else {
		printHannoiTower1(n - 1, from, help, to);//把1~1-N层从A->C，A为源，B为辅助，C为目的
		printf("move %d from %s to %s\n", n, from, to);//N可以顺利达到target，只需要1步完成
		printHannoiTower1(n - 1, help, to, from);//把1~N-1层从C->B，A为辅助，B为目的，C为源
	}
}
//思路2
void printHannoiTower2(int n, char from[], char help[], char to[]) {//将1~N层从A->C，     A为源，B作为辅助，C为目的 角色在变化
	if (n==1) {
		printf("move %d from %s to %s\n", n, from, to);//把第N层从A->C
		return;
	}
	else {
		printHannoiTower2(n - 1, from, to, help);//把1~1-N层从A->B，A为源，B为目的，C为辅助
		printf("move %d from %s to %s\n", n, from, to);//N可以顺利达到target，只需要1步完成
		printHannoiTower2(n - 1, help, from, to);//把1~N-1层从B->C，A为辅助，B作为源，C作为目的
	}
}
int main()
{
	printHannoiTower1(3, "A", "B", "C");
	printf("------------------\n");
	printHannoiTower2(3, "A", "B", "C");
	return 0;
}

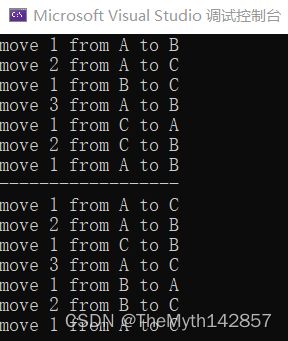
运行结果：

 java语言实现：

package com.themyth.test;
/**
 * 找重复：
 *      1.找到一种划分方法
 *      2.找到递推公式或者等价转化
 *      都是父问题转化为求解子问题
 * 找变化的量：
 *      变化的量通常要作为参数
 * 找出口：
 *      根据参数变化的趋势，对边界进行控制，适时终止递归
 *思路1：
 *      将1~N层从A->B，     A为源，B为目的，C作为辅助 角色在变化
 *      等价于
 *      1、把1~1-N层从A->C，A为源，B为辅助，C为目的
 *      2、把第N层从A->B
 *      3、把1~N-1层从C->B，A为辅助，B为目的，C为源
 * 思路2：
 *      将1~N层从A->C，     A为源，B作为辅助，C为目的 角色在变化
 *      等价于
 *      1、把1~1-N层从A->B，A为源，B为目的，C为辅助
 *      2、把第N层从A->C
 *      3、把1~N-1层从B->C，A为辅助，B作为源，C作为目的
 *
 */
/**
 * 将N个盘子从source移动到target的路径的打印
 *
  N      初始的N个从小到大的盘子，N是最大编号
  from   原始柱子
  to     目标柱子
  help   辅助的主子
 */
public class 汉诺塔 {
    public static void main(String[] args) {
        //思路1：C作为辅助
        printHannoiTower1(3,"A","B","C");
        System.out.println("----------------------------");
        //思路2：B作为辅助
        printHannoiTower2(3,"A","B","C");
    }
    //注意角色的变化
    private static void printHannoiTower1(int N, String from, String to, String help) {//    from源、to目的、help辅助
        if (N == 1) {
            System.out.println("move " + N + " from " + from + " to " + to);
            return;
        }else {
            printHannoiTower1(N-1,from,help,to);//   先把N-1个盘子移动到辅助空间上去，源、辅助、目的
            System.out.println("move " + N + " from " + from + " to " + to);//  N可以顺利达到target，只需要1步完成
            printHannoiTower1(N-1,help,to,from);// 让N-1从辅助空间回到源空间上，辅助、目的、源
        }
    }
    private static void printHannoiTower2(int N, String from, String help, String to) {//    from源、help辅助、to目的
        if (N == 1){
            System.out.println("move " + N + " from " + from + " to " + to);
            return;
        }else {
            printHannoiTower2(N-1,from,to,help);//   先把N-1个盘子移动到辅助空间上去，源、目的、辅助
            System.out.println("move " + N + " from " + from + " to " + to);//  N可以顺利达到target，只需要1步完成
            printHannoiTower2(N-1,help,from,to);// 让N-1从辅助空间回到源空间上，辅助、源、目的
        }
    }
}

运行结果：