【2022研究生数模 二等奖】汽车制造涂装-总装缓存调序区调度优化建模
汽车制造涂装-总装缓存调序区调度优化建模
- 摘要
- 1 问题重述
-
- 1.1 问题背景
- 1.2 问题的提出
- 2 模型假设、相关定义与符号
-
- 2.1 模型的假设
- 2.2 相关符号及定义
- 3 问题分析
-
- 3.1 针对问题1
- 3.2 针对问题2
- 4 问题一的模型建立与求解
-
- 4.1 模型的建立
-
- 4.1.1 确定目标函数
- 4.1.2 确定约束条件
- 4.2 算法描述
-
- 4.2.1 改进的遗传算法
- 4.2.2 基于统计的建模
- 4.3 算例分析
- 4.4 附件一算例求解
- 4.5 附件二算例求解
- 5 问题二的模型建立与求解
-
- 5.1 模型的建立
-
- 5.1.1 确定目标函数
- 5.1.2 确定约束条件
- 5.2 算法描述
-
- 5.2.1 统计建模方法的改进
- 5.3 算例分析
- 5.4 附件一算例求解
- 5.5 附件二算例求解
- 6 模型评价与未来展望
-
- 6.1 模型评价
-
- 6.1.1 模型的优点
- 6.1.2 模型的缺点
摘要
近年来,随着化石能源的逐步枯竭以及环境治理需求的急剧提升,新能源汽车产业作为中国战略性新兴产业获得了快速发展。在"碳中和、碳达峰"的大背景下,新能源汽车产业的发展是中国由汽车大国跻身于汽车强国的必经之路。与此同时,学术界以及大众给予该行业广泛关注,柔性生产这一概念亦被普及。越来越多样的定制化服务使人们能够以经济的价格,获得具有个性的汽车产品。在柔性生产的背景下,多车间之间的不同约束,尤其是涂装车间与总装车间的序列差异,导致生产调度无法按照同一序列连续生产。因此,如何在不同车间之间的PBS(Painted Body Store,汽车制造涂装-总装缓存调序区)高效完成调序任务显得尤为重要。针对此问题,本文从汽车流水线的实际约束出发,建立了**单目标整数规划模型,**用于解决PBS调序难问题,满足总装车间序列条件,降低调序耗时,从而切实匹配实际生产需要。
针对问题一,分析输出矩阵的规模复杂度,引入指令序列的概念,创建二维输出矩阵在一维空间中的同构表示,并据此大幅压缩可能的解空间。指令序列包含在时间上连续的横移机所要执行指令,这简化了PBS调序过程,并使得调序策略更为简洁,方便后续模型的建立与求解。同时,基于统计数据,设立启发式规则,根据具体赋分的启发信息对模型进行求解。在满足约束的条件下,针对附件二数据,此时总得分为32.8370,其中,目标一得分-48分,目标二得分82分,目标三得分100分,目标四得分74.37分,程序运行时间不到5分钟。
**针对问题二,**在去掉第6、7条约束后,即接车横移机空闲时优先处理返回车道10停车位的车身,以及送车横移机优先处理最先到达1停车位的车身,本文首先将车辆到达进车道尽头的到达序列延拓为在横移机到达指定位置前到达的即将到达序列,并在此序列中计算效率损耗,选取最高效的指令序列。在满足约束的条件下,针对附件二数据,此时总得分为32.7830,其中,目标一得分-48分,目标二得分82分,目标三得分100分,目标四得分73.83分,程序运行时间不到5分钟。
1 问题重述
1.1 问题背景
汽车制造厂主要由冲压车间、焊装车间、涂装车间、总装车间构成,每个车间有不同的生产功能与偏好。为了提高企业供应链生产的效率,生产调度功能对于优化资源配置、提高运作效率具有极为重要的意义。消费者的选择不同,汽车制造企业的投产订单也会随之发生变化,为了企业生产效率最大化,汽车制造厂的各个车间需要进行精确的生产调度。其中,涂装车间处理喷漆工艺,主要是将涂料涂覆于白车身表面,经过前处理电泳、中涂、色漆、清漆等环节,最终形成涂膜或者漆膜或者涂层。总装车间处理装配工艺,主要是组装内饰线、底盘线、最终等剩余零部件,并且最终经过测试检验后,才能得到最终的成品车辆。
由于各车间的约束不同导致生产调度无法按照同一序列连续生产,特别是涂装车间与总装车间序列差异较大,这就需要在两个车间之间建立一个具有调序功能的缓存区,即PBS(Painted Body Store,汽车制造涂装-总装缓存调序区),用来将涂装车间的出车序列调整到满足总装车间约束的进车序列。因此按照不同的PBS约束说明及相关时间数据说明,再根据涂装出车序列,考虑PBS区域调度能力及限制,建立PBS优化调度模型就显得极为重要。
PBS由涂装-PBS出车口、接车横移机、进车道6条(每条进车道有10个停车位、FIFO结构)、返回道1条(有10个停车位)、送车横移机及PBS-总装接车口等7个区域组成。每车道距离等分,各车道宽度2米,两相邻车道间间隔1米。横移机运动时的速度必须保持一致。根据涂装车间的出车序列,PBS调度调整得到总装车间的进车序列,从而使资源利用率达到最大化。
1.2 问题的提出
本文的宗旨是根据PBS约束条件,针对特定的优化目标建立遗传算法,启发式算法等算法,将涂装车间的出车序列进行调整,车辆以不同的决策进入不同的车道,总装车间利用率最大化。
问题一:
依托涂装车间出车序列,忽略车身由横移机卸载到各进车道、从车道装载到横移机上的时间;进车过程与出车过程横移机把车身从进车道4位置运送至不同进车道的停车位上并返回至初始位置,均以6s为一个间隔;车进返回道过程与车出返回道过程横移机从中间初始位置出发把各进车道1停车位的车身,运送至返回道1停车位,与把返回道10停车位的车身,运送至任意进车道10停车位并返回至初始位置的时间间隔均为6s;并规定从某一停车位移动至后一停车位,消耗时间为
9秒。同时按照约束条件构建 PBS
优化调度模型,使得从涂装车间进车序列能够更为高效的满足总装车间的生产需求。
问题二:
在问题1的基础上,PBS接车、送车横移机的运动轨迹,PBS的时间约束与规定都保持不变,只是约束条件有所改变。本题的约束条件只限制在送车横移机不能将返回道的车身送入PBS-总装接车口;车身在进车道和返回道的移动方向在选定一个车道后只能沿着这条车道运动;横移机上同一时刻只能有一个车身,在执行任何动作过程中,均不能被打断,并在完成任意动作后,必须返回中间初始位置,才可以执行下一步动作;如果任意进车道1停车位有车身,那么送车横移机不能设置为空闲状态;各个车道每个时刻最多容纳10个车身,每个停车位最多容纳1个车身;车身在各个车道不同停车位之间移动的过程中,不能被调度等约束建立PBS优化调度模型,使得总装进车序列最大化满足总装生产车间的需求。
2 模型假设、相关定义与符号
2.1 模型的假设
-
PBS由涂装-PBS出车口、接车横移机、进车道6条(每条进车道有10个停车位、FIFO结构)、返回道1条(有10个停车位)、送车横移机及PBS-总装接车口等7个区域组成;
-
PBS接车横移机可以将车身从涂装-PBS出车口运送到合适进车道,也可以将车身从返回道运送到合适进车道;
-
PBS送车横移机可以将所选择车身从进车道运送到PBS-总装接车口,也可以将需调序车身从进车道运送到返回道;
-
当某车身所在停车位的下一停车位出现空位时,车身必须立即开始向下一停车位移动;
-
车身在进车道和返回道的移动方向为图中标注方向,不得改变;
-
进车道和返回道每个时刻最多容纳10个车身,每个停车位最多容纳1个车身;
-
同一车道内,多个车身在不同停车位上的移动可以不同步进行;
-
接车横移机和送车横移机上同一时刻分别最多有一个车身;
-
接车横移机和送车横移机在完成任意动作后,必须返回中间初始位置,才可以执行下一步动作;
-
接车横移机和送车横移机在执行任何动作过程中,均不能被打断;
-
送车横移机不能将返回道的车身送入PBS-总装接车口;
-
如果任意进车道1停车位有车身,那么送车横移机不能设置为空闲状态;
-
车身在进车道和返回道不同停车位之间移动的过程中,不能被调度;
-
各车道距离等分,每车道宽度2米,两相邻车道间间隔1米。横移机运动时的速度保持一致。
2.2 相关符号及定义
| 符号 | 说明 |
|---|---|
| μ = ( μ 1 , μ 2 , ⋯ , μ n ) \boldsymbol{\mu }=\left( \mu _1,\mu _2,\cdots ,\mu _n \right) μ=(μ1,μ2,⋯,μn) | 输入序列 |
| v = ( v 1 , v 2 , ⋯ , v n ) \mathbf{v}=\left( \mathrm{v}_1,\mathrm{v}_2,\cdots ,\mathrm{v}_n \right) v=(v1,v2,⋯,vn) | 输出序列 |
| t t t | 第 t t t时刻 |
| T T T | 总耗时 |
| c o u n t count count | 返回道使用次数 |
| s j i s_{j}^i sji | 第 i , j i,j i,j 个状态 |
| S = { s 0 0 , s 0 1 ⋯ s 10 7 } S=\{s_0^0,s_0^1\cdots s_{10}^7\} S={s00,s01⋯s107} | 状态集合,共74种状态 |
| P = { s 1 , s 2 ∣ s 1 , s 2 ∈ S } P=\{s1,s2\mid s1,s2\in S\} P={s1,s2∣s1,s2∈S} | 状态转移矩阵 |
| M s t M_s^t Mst | t t t 时刻,区域 s s s 上的车辆编号,没有车辆则为0 |
| R = { t , i ∣ t ∈ [ 0 , T ] , i ∈ [ 1 , n ] } R=\{t,i\mid t\in[0,T],i\in [1,n]\} R={t,i∣t∈[0,T],i∈[1,n]} | 输出结果矩阵, R i t R^t_i Rit表示 t t t时刻第 i i i辆车所在的区域 |
| Q 1 = { q 1 1 , q 2 1 , … , q 13 1 } Q1=\{q^1_1,q^1_2,\dots,q^1_{13}\} Q1={q11,q21,…,q131} | 前6个指令为将车辆从PBS入口移至1-6车道10车位,后6个指令表示将返回道10车位的车辆移至1-6车道10车位,第13个指令为等待3秒 |
| Q 2 = { q 1 2 , q 2 2 , … , q 13 2 } Q2=\{q^2_1,q^2_2,\dots,q^2_{13}\} Q2={q12,q22,…,q132} | 前6个指令为将车辆从1-6车道1车位移至PBS出口,后6个指令表示将1-6车道1车位的车辆移至返回道1车位,第13个指令为等待3秒 |
| D j i = { d 1 , d 2 , … , d k } D_j^i=\{d_1,d_2,\dots,d_k\} Dji={d1,d2,…,dk} | 指令 q j i q^i_j qji对应的元操作序列, d k d_k dk表示指令执行后第 k k k秒横移机所在位置 |
| L 1 = { l 1 , l 2 , … , l e 1 } L1=\{l_1,l_2,\dots,l_{e1}\} L1={l1,l2,…,le1} | 接车横移机的指令执行序列 |
| L 2 { l 1 , l 2 , … , l e 2 } L2\{l_1,l_2,\dots,l_{e2}\} L2{l1,l2,…,le2} | 送车横移机的指令执行序列 |
| s t l st_{l} stl | 指令 l l l 的开始执行时间 |
| e n d l end_{l} endl | 指令 l l l 的结束执行时间 |
3 问题分析
3.1 针对问题1
首先将模型假设即约束条件,划分成车辆约束、横移约束与车道约束。其中车辆约束再分成限制性约束、强转移约束、非严格约束。限制性约束为限制了车辆在下一时刻可能的状态变化,车身在进车道和返回道一旦确定了车道,就确定了车辆的移动方向,车身在不同停车位之间移动的过程中,不能被调度,送车横移机只能将进车道(1-6)的车身送入PBS-总装接车口,却不能将返回道的车身送入PBS-总装接车口,因此可以建立状态转移矩阵或位置变化矩阵(图一);强转移约束为当某车身所在停车位的下一停车位出现空位时,车身必须立即开始向下一停车位移动;非严格约束为同一车道内,根据横移机移动所需时间、车身在停车位移动所需时间,多个车身在不同停车位上的移动可以不同步进行。横移约束再分成物理约束与命令约束。物理约束为横移机每时刻最多只能有一辆车。命令约束为横移机在执行任何动作过程中,均不能被打断且在完成任意动作后,必须返回中间初始位置,才可以执行下一步动作;当返回道10停车位有车身,同时接车横移机空闲时,优先处理返回道10停车位上的车身;当若干进车道1停车位有车身等候,同时送车横移机空闲时,优先处理最先到达1停车位的车身;如果任意进车道1停车位有车身,那么送车横移机不能设置为空闲状态。车道约束由于每道只有10个车位,所以只要能保证每个车位只有一辆车,就可以保证每道车辆小于等于10.严格按照约束条件以及PBS时间数据,对于四个优化目标进行分析,并最终构造一个总的目标函数,使得惩罚最小,最大化满足优化目标。
3.2 针对问题2
在问题1的基础上,保持PBS时间数据、四个优化目标不变,将约束条件中横移约束的命令条件进行缩小,即删去约束条件:1)当返回道10停车位有车身,同时接车横移机空闲时,优先处理返回道10停车位上的车身;2)当若干进车道1停车位有车身等候,同时送车横移机空闲时,优先处理最先到达1停车位的车身。将这两个约束除去后,其余约束条件保持不变。根据涂装车间出车序列,考虑PBS区域调度能力及限制,建立PBS优化调度模型,使得总装进车序列尽可能满足总装生产需求。
4 问题一的模型建立与求解
4.1 模型的建立
4.1.1 确定目标函数
以题中给出的优化目标为基础,本文列出的规划方程如下所示。
总优化目标:
令四个优化目标的初始分数均为100,经过计算处理后各优化目标分别以
f 1 , f 2 , f 3 f_1 , f_2 , f_3 f1,f2,f3 和 f 4 f_4 f4 表示, 将它们分别乘以对应的权重系数,
从而得到最后的总优化目标。
max f = 0.4 f 1 + 0.3 f 2 + 0.2 f 3 + 0.1 f 4 \max f=0.4 f_1+0.3 f_2+0.2 f_3+0.1 f_4 maxf=0.4f1+0.3f2+0.2f3+0.1f4
优化目标1:
优化目标1为若每连续两辆混动车身之间的非混动车型为2台则为优,不扣分。
f 1 = 100 − ∑ i = 1 n δ 1 ( v i ) δ 2 ( v i ) f_1=100-\sum_{i=1}^n \delta_1\left(\mathrm{v}_i\right) \delta_2\left(\mathrm{v}_i\right) f1=100−i=1∑nδ1(vi)δ2(vi)
其中
δ 1 ( v i ) = { 1 , v i = 混动 0 , v i = 燃油 \delta_1\left(\mathrm{v}_{\mathrm{i}}\right)= \begin{cases}1 & , \mathrm{v}_{\mathrm{i}}=\text { 混动 } \\ 0, & \mathrm{v}_{\mathrm{i}}=\text { 燃油 }\end{cases} δ1(vi)={10,,vi= 混动 vi= 燃油
δ 2 ( v i ) = { 0 , v i , v i + 3 = 混动且 v i + 1 , v i + 2 = 燃油 1 , ,其他 \delta_2\left(\mathrm{v}_i\right)= \begin{cases}0 & , \mathrm{v}_i, \mathrm{v}_{i+3}=\text { 混动且 } \mathrm{v}_{i+1}, \mathrm{v}_{i+2}=\text { 燃油 } \\ 1, & \text {,其他 }\end{cases} δ2(vi)={01,,vi,vi+3= 混动且 vi+1,vi+2= 燃油 ,其他
优化目标2:
优化目标2是对出车序列进行分块,若每一分块中的四驱车型和二驱车型的比例不为1,则需要扣1分。
f 2 = ∑ i = 1 k g ( b i ) f_2=\sum_{i=1}^k{g\left( b_i \right)} f2=i=1∑kg(bi)
其中, k k k 为输出序列根据题目要求分成的段数, b i b_i bi 为第 i i i 段
g ( b i ) = δ ( ∑ j = 1 l δ 3 ( b i j ) − l 2 ) g\left(b_i\right)=\delta\left(\sum_{j=1}^l \delta_3\left(b_{i j}\right)-\frac{l}{2}\right) g(bi)=δ(j=1∑lδ3(bij)−2l)
其中, b i j b_{ij} bij 为第 i i i 段的第 j j j 个输出车型
δ 3 ( b i j ) = { 1 , b i j = 双驱 0 , b i j = 四驱 \delta_3\left(b_{i j}\right)= \begin{cases}1 & , b_{i j}=\text { 双驱 } \\ 0 & , b_{i j}=\text { 四驱 }\end{cases} δ3(bij)={10,bij= 双驱 ,bij= 四驱
优化目标3:
优化目标3是每使用一次返回道就需要扣1分。
f 3 = 100 − c o u n t f_3=100-count f3=100−count
优化目标4:
优化目标4是若出车列长度为C,从第一辆车身进图涂装-PBS出车口到最后一个车身进入PBS-总装借车口的总时间为T,理论上最快完成的时间为9C+72,时间惩罚值为0.01×(T-9C-72)。因此,最后的目标分为100-时间惩罚值。
f 4 = 100 − 0.01 ( T − 9 C − 72 ) f_4=100-0.01\left( T-9C-72 \right) f4=100−0.01(T−9C−72)
4.1.2 确定约束条件
1. 限制性约束
约束1、2、12均限制了车辆在下一时刻可能的状态变化,因此可以建立状态转移矩阵或者说位置变化矩阵 P = { s 1 , s 2 ∣ s 1 , s 2 ∈ S } P=\{s1,s2\mid s1,s2\in S\} P={s1,s2∣s1,s2∈S} 当且仅当 P s 1 , s 2 = 1 P_{s1,s2}=1 Ps1,s2=1 时 s i s_i si可以在下个状态转换为 s j s_j sj ,或者说从 s i s_i si 位置移动至 s j s_j sj 位置。于是,根据题目可得相应约束表示如下:
约束条件1
约束条件1为送车横移机只能将进车道上的车身运送到PBS-总装接车口,而不能将返回道上的车身运送到借车口。
P s j 7 , s 2 0 = 0 , j ∈ [ 1 , 10 ] P_{s_j^7, s_2^0}=0, j \in[1,10] Psj7,s20=0,j∈[1,10]
约束条件2
约束2为车身在进车道和返回道上的移动方向均为箭头标注的方向,不可以逆向移动。
- 进车道约束
∀ i ∈ [ 1 , 6 ] , P s j 1 i , s j 2 1 = { 1 , j 1 − j 2 ∈ [ 1 , 0 ] 0 , , 其他 \forall i \in[1,6], P_{s_{j 1}^i, s_{j 2}^1}= \begin{cases}1 & , j 1-j 2 \in[1,0] \\ 0, & \text {, 其他 }\end{cases} ∀i∈[1,6],Psj1i,sj21={10,,j1−j2∈[1,0], 其他
- 返回道约束
P s j 1 7 , s j 2 ⊤ = { 1 , j 2 − j 1 ∈ [ 1 , 0 ] 0 , 其他 P_{s_{j 1}^7, s_{j 2}^{\top}}= \begin{cases}1, & j 2-j 1 \in[1,0] \\ 0, & \text { 其他 }\end{cases} Psj17,sj2⊤={1,0,j2−j1∈[1,0] 其他
约束条件12
- 进车道约束
∀ i ∈ [ 1 , 6 ] , P s j 1 i , s j 2 0 = { 1 , j 1 = 1 ∩ j 2 = 2 0 , , 其他 \forall i \in[1,6], P_{s_{j 1}^i, s_{j 2}^0}= \begin{cases}1 & , j 1=1 \cap j 2=2 \\ 0, & \text {, 其他 }\end{cases} ∀i∈[1,6],Psj1i,sj20={10,,j1=1∩j2=2, 其他
- 返回道约束
P s j 1 7 , s j 2 0 = { 1 , j 1 = 10 ∩ j 2 = 1 0 , 其他 P_{s_{j 1}^7, s_{j 2}^0}= \begin{cases}1 & , j 1=10 \cap j 2=1 \\ 0 & , \text { 其他 }\end{cases} Psj17,sj20={10,j1=10∩j2=1, 其他
2. 强制转移约束
约束条件11
约束11给出了一个车辆必须转移状态的环境,当下一停车位有空闲时,车身需立即向下一车位移动。此过程可以表述如下:
- 进车道约束
当 ∀ i ∈ [ 1 , 6 ] ∀ j ∈ [ 2 , 10 ] , M s j i t = n ∩ M s j + 1 i t = m ∩ M s j + 1 i t + 1 = 0 \forall i\in \left[ 1,6 \right] \forall j\in \left[ 2,10 \right] ,M_{s_{j}^{i}}^{t}=n\cap M_{s_{j+1}^{i}}^{t}=m\cap M_{s_{j+1}^{i}}^{t+1}=0 ∀i∈[1,6]∀j∈[2,10],Msjit=n∩Msj+1it=m∩Msj+1it+1=0时
M s j + 1 i t + 1 = n M s j i t + 1 = 0 \begin{aligned} M_{s_{j+1}^{i}}^{t+1}&=n\\ M_{s_{j}^{i}}^{t+1}&=0 \end{aligned} Msj+1it+1Msjit+1=n=0
- 返回道约束
当 ∀ j ∈ [ 1 , 9 ] , M s j 7 t = n ∩ M s j − 1 7 t = m ∩ M s j − 1 7 t + 1 = 0 \forall j\in \left[ 1,9 \right] ,M_{s_{j}^{7}}^{t}=n\cap M_{s_{j-1}^{7}}^{t}=m\cap M_{s_{j-1}^{7}}^{t+1}=0 ∀j∈[1,9],Msj7t=n∩Msj−17t=m∩Msj−17t+1=0时
M s j − 1 i t + 1 = n M s j i t + 1 = 0 \begin{aligned} M_{s_{j-1}^{i}}^{t+1}&=n\\ M_{s_{j}^{i}}^{t+1}&=0 \end{aligned} Msj−1it+1Msjit+1=n=0
3. 非严格约束
约束条件10
约束10表示不同停车位上车身的移动可以不同步,并没有缩小问题解空间,并不是数学意义上的约束条件,因此这里不对其进行数学建模。
4. 物理约束
约束条件3
约束3限制了横移机上每时刻最多只能有一辆车,可以表示如下:
- 接车横移机
∀ t ∈ [ 0 , T ] , ∑ i = 1 n δ ( R i t − s 1 0 ) ⩽ 1 \forall t \in[0, T], \sum_{i=1}^n \delta\left(R_i^t-s_1^0\right) \leqslant 1 ∀t∈[0,T],i=1∑nδ(Rit−s10)⩽1
- 送车横移机
∀ t ∈ [ 0 , T ] , ∑ i = 1 n δ ( R i t − s 2 0 ) ⩽ 1 \forall t \in[0, T], \sum_{i=1}^n \delta\left(R_i^t-s_2^0\right) \leqslant 1 ∀t∈[0,T],i=1∑nδ(Rit−s20)⩽1
5. 命令约束
约束4、5、6、7、8均为横移机所要服从的机械指令,由于我们忽视了车辆在横移机、车道、PBS间转移所消耗的时间,因此,不妨设接车横移机指令集为 Q 1 = { q 1 1 , q 2 1 , … , q 12 1 } Q1=\{q^1_1,q^1_2,\dots,q^1_{12}\} Q1={q11,q21,…,q121}其中,前6个指令为将车辆从PBS移至1-6车道10车位,后6个指令表示将返回道10车位的车辆移至1-6车道10车位。相应的,设送车横移机指令集为 Q 2 = { q 1 2 , q 2 2 , … , q 12 2 } Q2=\{q^2_1,q^2_2,\dots,q^2_{12}\} Q2={q12,q22,…,q122}其中,前6个指令为将车辆从1-6车道1车位移至PBS,后6个指令表示将1-6车道1车位的车辆移至返回道1车位。同时,设每个指令 q j i q^i_j qji 对应的元操作序列为 D j i = { d 1 , d 2 , … , d k } D_j^i=\{d_1,d_2,\dots,d_k\} Dji={d1,d2,…,dk},同时,对于两个横移机各有一个指令执行序列 L 1 = { l 1 , l 2 , … , l e 1 } L1=\{l_1,l_2,\dots,l_{e1}\} L1={l1,l2,…,le1} L 2 { l 1 , l 2 , … , l e 2 } L2\{l_1,l_2,\dots,l_{e2}\} L2{l1,l2,…,le2},横移机将按顺序执行其中的指令。
约束条件4
约束4表示接车和送车横移机在完成接送任务以及其他动作后,必须返回初始中间位置,接着执行下完的操作。
∀ D j i , d k = 4 \forall D_j^i, d_k=4 ∀Dji,dk=4
约束条件5
约束5表示接车和送车横移机在执行动作过程中均不能被打断。
∀ l i , s t l i > e n d l i − 1 \forall l_i, s t_{l_i}>e n d_{l_{i-1}} ∀li,stli>endli−1
其中 s t l st_{l} stl 为指令 l l l 的起始执行时间, e n d l end_{l} endl 为指令 l l l的执行结束时间。
约束条件6
约束6表示接车横移机空闲时需要优先处理返回道10停车位上的车身。
∀ l ∈ Q 1 , 当 M s 10 7 end l i ≠ 0 时, l i + 1 ∈ { q 7 1 , q 8 1 , ⋯ , q 12 1 } \forall l \in Q 1 \text {, 当 } M_{s_{10}^7}^{\text {end }_{l_i}} \neq 0 \text { 时, } l_{i+1} \in\left\{q_7^1, q_8^1, \cdots, q_{12}^1\right\} ∀l∈Q1, 当 Ms107end li=0 时, li+1∈{q71,q81,⋯,q121}
歧义:在这里,"空闲"被定义为刚执行完上一条指令,等待下一条指令。(如果被定义为:没有其他指令可以被执行。结果会发生变化)
约束条件7、8
约束7和8表示送车横移机空闲时需要优先处理最先到达1停车位的车身。同时,只要进车道1停车位有车,则送车横移机就不设为空闲状态。
∀ l ∈ Q 2 , ∀ j ∈ [ 1 , 6 ] , 当 M s 1 j e ndd d i i ≠ 0 时, l i + 1 = q k + 6 2 \forall l \in Q 2, \forall j \in[1,6] \text {, 当 } M_{s_1^j}^{e \operatorname{ndd} d_{i_i}} \neq 0 \text { 时, } l_{i+1}=q_{k+6}^2 ∀l∈Q2,∀j∈[1,6], 当 Ms1jendddii=0 时, li+1=qk+62
其中, k k k 为最先到达1停车位的车辆所在的车道
约束条件9
由于每道只有10个车位,所以只要能保证每个车位只有一辆车,就可以保证每道车辆小于等于10.于是可表示如下:
∀ t ∈ [ 0 , T ] , ∀ j ∈ [ 1 , 7 ] , ∀ k ∈ [ 1 , 10 ] , ∑ i = 1 n δ ( R i t − s k j ) ⩽ 1 \forall t \in[0, T], \forall j \in[1,7], \forall k \in[1,10], \sum_{i=1}^n \delta\left(R_i^t-s_k^j\right) \leqslant 1 ∀t∈[0,T],∀j∈[1,7],∀k∈[1,10],i=1∑nδ(Rit−skj)⩽1
4.2 算法描述
4.2.1 改进的遗传算法
汽车制造涂装-总装缓存PBS调度优化问题属于优化理论范畴的NP-hard问题,由于其解领域较难表达且解空间非连续,一般算法难以求解,因此遗传算法是一种较优的选择[1]。Holland于1970年提出了这种依托于生物界遗传学原理和自然选择的随机搜索算法。此算法在解决非线性问题上能够跳出局部最优解,从而获得全局最优解由于拥有高稳健性、全局能力强等特点,被广泛应用于各领域。本文针对车间PBS优化问题,提出了改进遗传算法:(1)以传统遗传算法为基础构建了一种特殊编码方式。(2)提出了适应该编码方式的交叉算子以及变异算子的设计。(3)融合父代与子代操作,以免丢失局部最优解。综上,该算法由编码方式、交叉、变异、染色体调整以及适应度函数构成。
1. 要求输出
题目要求,输出一个 R = n ∗ T R=n * T R=n∗T 的矩阵。这个矩阵的长为 T T T即整个流程消耗的时间,是一个末知量; 这个矩阵的宽为 n n n即转移车辆的数量,根据附件可知 n = 318 n=318 n=318 。
2. T的确定
T T T 作为一个未知量,使得问题规模难以确定,不利于问题求解,由于题目给出了 T T T 的下界,于是自然想到,可否通过某些方式,来找到 T T T的上界。
对于 ∀ n ⩾ 74 \forall n\geqslant 74 ∀n⩾74 ,即当 n n n大于整个PBS可以容纳的车辆数时,考虑极端情况,我们希望把第74辆车调整为第一个运出的车辆,那么为了将前73辆车存储在PBS中,我们需要消耗90*2+(18+12+12+18)*10s,在这种极端情况下,调度时间最长的车为刚进入返回车道的车辆,如果要将这辆车作为下一辆出PBS车,那么可以将返回车道与进车道4视为一个循环车道,那么可以得到,需要的耗时为180s,于是,我们可以证明,为了调整车序所需的时间上界为
180 ∗ ( C − 73 ) + 90 ∗ 2 + ( 18 + 12 + 12 + 18 ) ∗ 10 = 180 C − 12360 180*(C-73)+90*2+(18+12+12+18)*10 = 180C-12360 180∗(C−73)+90∗2+(18+12+12+18)∗10=180C−12360 于是,我们可以确定 T ∈ [ 9 C − 72 , 180 C − 12360 ] T\in \left[ 9C-72,180C-12360 \right] T∈[9C−72,180C−12360] .而对于任意 T > 180 C − 12360 T>180C-12360 T>180C−12360的策略,我们都可以找到一个耗时更短的策略,却可以达成同样输出序列的策略。
3. 压缩解空间
如果以 T T T 的上界为输出结果的长,那么可能的解空间高达 74 180 C 2 − 12360 C {74}^{180C^2-12360C} 74180C2−12360C,依然是非常庞大的,同时各个变量之间的相关性非常强烈,不利于问题求解。
为了压缩解空间,降低变量复杂度,本文提出以横移台的指令序列作为解空间的方法。指令序列定义: L = { l 1 , l 2 , … , l k , l k + 1 , l k + 2 … l 2 k } L=\{l_1,l_2,\dots,l_k,l_{k+1},l_{k+2} \dots l_{2k}\} L={l1,l2,…,lk,lk+1,lk+2…l2k},指令集 L L L可分割为:
送车横移台执行指令序列为 L 1 = { l 1 , l 2 , … , l k } L1=\{l_1,l_2,\dots,l_{k}\} L1={l1,l2,…,lk} ;
接车横移台执行指令序列为 L 2 = { l k + 1 , l k + 2 , … , l 2 k } L2=\{l_{k+1},l_{k+2},\dots,l_{2k}\} L2={lk+1,lk+2,…,l2k} 。
执行指令序列中的指令连续执行,在上一个指令执行完后(即横移机回到初始位置后)立刻执行下一条指令。同时,假设两台横移机都在最后一辆车移出PBS时停止工作,于是可得
k k k 的上界为 T T T 的上界再除以最短命令。即
⌈ k ⌉ ⩽ ⌈ T ⌉ min ( L ) \lceil k\rceil \leqslant \frac{\lceil T\rceil}{\min (L)} ⌈k⌉⩽min(L)⌈T⌉
当我们知道了题目要求的结果矩阵 R R R,我们可以通过车辆移动的变化知道横移台的运动情况,即可推导出横移台所执行的指令序列。而如果知道了横移台所执行的指令序列 L L L以及指令执行的时间,那么我们也同样可以还原出车辆移动的情况。也就是说,我们可以在指令序列与结果矩阵之间构造出一个双射函数。这也证明了指令序列 L L L 与结果矩阵 R R R 是同构的,或者说指令序列 L L L 是结果矩阵 R R R的低维流形。我们先求解 L L L ,然后将 L L L 映射到 R R R
所在空间即可得到最终答案。
由于,两个横移机可执行指令各为12个,考虑再加入一个等待指令,指令时长取所有操作的最大公约数3,此时,问题规模就变成了 13 2 k {13}^{2k} 132k ,而其中 ⌈ k ⌉ ⩽ 180 C − 12360 3 = 60 C − 4120 \lceil k \rceil \,\,\leqslant \frac{180C-12360}{3}=60C-4120 ⌈k⌉⩽3180C−12360=60C−4120,于是可以得到目前的问题规模为 13 60 C − 4120 {13}^{60C-4120} 1360C−4120 问题规模大大缩小了。
4. 交叉
交叉操作的主要目的以保持优良基因为前提,再进行相关操作后产生新的个体。本文所采用的交叉方式为基于位置的交叉。具体方法为在一个父代染色体上随机选择多个交叉位置的基因并将其保留,剔除其他基因。接着在第二个父代染色体上找出除该位置外的其他基因,并插入到保留基因中,从而形成第一个子代。接着再用此方法对第二个父代形成此操作,以此类推。
5. 变异
变异操作的主要目的是通过小幅度干扰染色体来形成新个体,一定程度上保证种族多样性,影响局部搜索能力。本文主要通过在变异个体上随机选择位置进行基因互换,从而形成新个体。
6. 染色体调整策略
算法每次迭代后都会产生一个当代最优解,而该最优解就会产生一个新的种群。然而该种群可能存在不可行的解。此时需要对染色体进行一定程度的调整。
7. 选择及适应度计算
适应度是衡量种群染色体优劣的标准,适应度越高的个体有更高的概率被保留并遗传给下一代。本文适应度计算公式如下:
f = 1 0.4 f 1 + 0.3 f 2 + 0.2 f 3 + 0.1 f 4 f=\frac{1}{ 0.4f_1 + 0.3f_2 + 0.2f_3 + 0.1f_4 } f=0.4f1+0.3f2+0.2f3+0.1f41
本文的目标函数一共包括 4 个,对四个目标进行求和, 所得出的倒数即
为该染色体的适应度值。
4.2.2 基于统计的建模
1. 统计数据
| 统计对象 | 数量 |
|---|---|
| 燃油、两驱 | 77 |
| 燃油、四驱 | 29 |
| 混动、两驱 | 212 |
| 混动、四驱 | 0 |
根据附件一数据统计,共318辆汽车。
2. 分析
在本题中,需要纳入考量的车辆差异有两种:动力和驱动;而且,题目所给环境中共有6条前进车道,因此,容易想到,可以根据不同车型来分配其车道。
理想情况下,为使车辆转移所消耗的时间最短,即求解如下规划方程: min ∑ i = 1 4 t i n i \min \sum_{i=1}^4{t_in_i} min∑i=14tini,其中 t i t_i ti
表示第 i i i 类车转移所需的时间, n i n_i ni 表示第
i i i类车的数量,根据题目所给消耗时间矩阵:PBS进-进车道[18,12,6,0,12,18];进车道-PBS出:[18,12,6,0,12,18],可得车道优先级如下:4>3>2=5>1=6.同时,考虑车进返回道的时间消耗,根据题目所给消耗时间矩阵:返回道-进车道[24,18,12,6,12,18];进车道-返回道:[24,18,12,6,12,18],可得车道优先级如下:4>3=5>2=6>1.因此,根据统计结果,设计车道分配结果如下:
| 车型 | 数量 | 车道 |
|---|---|---|
| 燃油、两驱 | 77 | 3 |
| 燃油、四驱 | 29 | 5 |
| 混动、两驱 | 212 | 4 |
| 混动、四驱 | 0 | 2 |
其中,1、6车道为备用车道,当其他车道满员无法进入时再使用。
3. 接车横移机策略
接车横移机的决策树可以表示如下:
输入:R
输出:code
while 有车需要被调度 do
if 返回道10车位有车 then
car=car_in_return_lane % 返回道10车位的车
else if PBS入口有车 then
car=car_in_PBS_entrance
else
code=13 % 等待
code = move11(car,type)%转移车,type表示车是在PBS入口0还是返回道1
其中,move11()函数可以表示如下:
输入:car type
输出:code
if car.power == 燃油 then
if car.drive == 两驱 then
lane=3
else
lane=5
else
if car.drive == 两驱 then
lane=4
else
lane=2
if map(lane,10)==0 then % 目标车位闲置
code=lane+type*6
else if map(1,10)==0 then % 目标车位有车,停到备用车道1
code=1+type*6
else if map(6,10)==0 then
code=6+type*6
else
code=13 % 等待
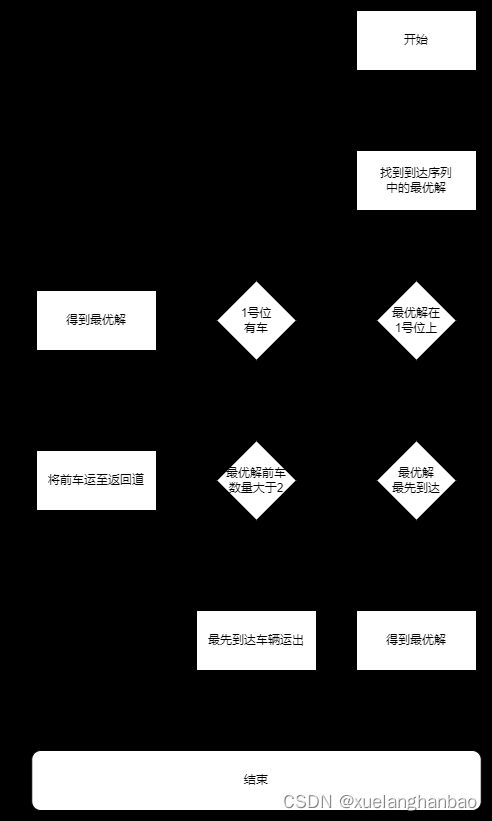
4. 送车横移机策略
对于送车横移机,只需要考虑目前可执行命令以及已输出序列,并根据次作出决策即可。
对于优化目标一,根据统计结果可知,混动车的数量是大于燃油车的,因此,无法完全满足优化目标一,在设计策略时应当尽可能地避免在混动车后放入一辆燃油车或超过三辆燃油车,因为这样的行为会导致本就不够的燃油车更加稀缺。每出现一次这种情况,扣分为0.4
对于优化目标二,根据统计结果可知,二驱车的数量与四驱车的数量是差不多的,因此,可以尽量满足其要求。不满足时,扣分为0.3
对于优化目标三和四,当有一辆车被送入返回车道时,考虑最优情况,即这辆车原本在第4车道,同时,从返回道出来后也直接进入第4车道,此时,将产生如下扣分:
-
使用返回道的扣分 0.2
-
由于时间延长而导致的扣分,考虑最好情况,即相当于多一辆车的转移时间为9s,扣分为0.009
于是,我们可以知道,放一辆车进入返回道这个操作就导致的扣分下界为0.209,同时,当剩余车辆小于20辆时,扣分下界就会开始上升,具体分数为 0.09 ( 21 − n ) + 0.2 = 2.09 − 0.09 n 0.09\left( 21-n \right) +0.2=2.09-0.09n 0.09(21−n)+0.2=2.09−0.09n
可以设计送车横移机策略如下:
输入:u v n % 到达队列,每个车道1号位的车按到达顺序排列在此队列中 输出序列 剩余车辆数
输出:code
if 有车需要被调度 then
code=move12(u,v,n)
else
code=13
其中,move12()函数可以表示如下:
4.3 算例分析
由于压缩后的解空间规模依然十分庞大,因此,遗传算法需要花费大量时间用于求解。而基于规则的统计建模方法则相对更加灵活,取得了更加优秀的成绩。各算例求解如下所示。
4.4 附件一算例求解
| 指标 | 基于统计的建模 | 遗传算法 |
|---|---|---|
| 总目标 | 9.878 | 8.046 |
| 目标一 | -103 | -103 |
| 目标二 | 82 | 82 |
| 目标三 | 100 | 100 |
| 目标四 | 64.78 | 46.46 |
| 运行时间 | 321.611 | 3273.587 |
4.5 附件二算例求解
| 指标 | 基于统计的建模 | 遗传算法 |
|---|---|---|
| 总目标 | 32.8370 | 29.72 |
| 目标一 | -48 | -48 |
| 目标二 | 82 | 82 |
| 目标三 | 100 | 100 |
| 目标四 | 64.78 | 43.2 |
| 运行时间 | 284.755 | 3342.981 |
5 问题二的模型建立与求解
5.1 模型的建立
5.1.1 确定目标函数
优化目标1:混动车型间隔2台非混动车型为优,权重系数 0.4。
优化目标2:四驱车型与两驱车型倾向1:1出车序列,权重系数 0.3。
优化目标3:返回道使用次数倾向于0,权重系数 0.2。
优化目标4:倾向总调度时间越短越好,权重系数 0.1。
注:该权重系数用于多目标得分加权,各权重系数相加等于1。
根据上述优化目标的要求,建立目标函数如下所示
f ( x ) = { f 1 = 100 − ∑ i = 1 n δ 1 ( v i ) δ 2 ( v i ) f 2 = ∑ i = 1 k g ( b i ) f 3 = 100 − c o u n t f 4 = 100 − 0.01 ( T − 9 C − 72 ) \begin{aligned} f(x)=\left\{ \begin{aligned} f_1 & = 100-\sum_{i=1}^n \delta_1\left(\mathrm{v}_i\right) \delta_2\left(\mathrm{v}_i\right) \\ f_2 & = \sum_{i=1}^k{g\left( b_i \right)} \\ f_3 & = 100-count \\ f_4 & = 100-0.01\left( T-9C-72 \right) \\ \end{aligned} \right. \end{aligned} f(x)=⎩ ⎨ ⎧f1f2f3f4=100−i=1∑nδ1(vi)δ2(vi)=i=1∑kg(bi)=100−count=100−0.01(T−9C−72)
总优化目标为:
max f = 0.4 f 1 + 0.3 f 2 + 0.2 f 3 + 0.1 f 4 \max f=0.4 f_1+0.3 f_2+0.2 f_3+0.1 f_4 maxf=0.4f1+0.3f2+0.2f3+0.1f4
5.1.2 确定约束条件
约束条件1
送车横移机不能将返回道的车身送入PBS-总装接车口;
约束条件2
车身在进车道和返回道的移动方向为图中标注方向,不得改变;
约束条件3
接车横移机和送车横移机上同一时刻分别最多有一个车身;
约束条件4
接车横移机和送车横移机在完成任意动作后,必须返回中间初始位置,才可以执行下一步动作;
约束条件5
接车横移机和送车横移机在执行任何动作过程中,均不能被打断;
约束条件6
如果任意进车道1停车位有车身,那么送车横移机不能设置为空闲状态;
约束条件7
进车道和返回道每个时刻最多容纳10个车身,每个停车位最多容纳1个车身;
约束条件8
同一车道内,多个车身在不同停车位上的移动可以不同步进行;
约束条件9
当某车身所在停车位的下一停车位出现空位时,车身必须立即开始向下一停车位移动;
约束条件10
车身在进车道和返回道不同停车位之间移动的过程中,不能被调度.
根据上述送车横移机、接车横移机的执行动作,车身在车道运动的运动轨迹等约束条,得到如下:
s . t . { P s j 7 , s 2 0 = [ t ] 0 , j ∈ [ 1 , 10 ] P s j 1 i , s j 2 1 = [ t ] { 1 , j 1 − j 2 ∈ [ 1 , 0 ] 0 , , 其他 , ∀ i ∈ [ 1 , 6 ] P s j 1 7 , s j 2 ⊤ = [ t ] { 1 , j 2 − j , 1 ∈ [ 1 , 0 ] 0 , 其他 P s j 1 i , s j 2 0 = [ t ] { 1 , j 1 = 1 ∩ j 2 = 2 0 , , 其他 , ∀ i ∈ [ 1 , 6 ] P s j 1 7 , s j 2 0 = [ t ] { 1 , j 1 = 10 ∩ j 2 = 1 0 , 其他 ∑ i = 1 n δ ( R i t − s 1 0 ) ⩽ [ t ] 1 , ∀ t ∈ [ 0 , T ] ∑ i = 1 n δ ( R i t − s 2 0 ) ⩽ [ t ] 1 , ∀ t ∈ [ 0 , T ] d k = [ t ] 4 , ∀ D j i s t l i > [ t ] n d l i − 1 , ∀ l i ∑ i = 1 n δ ( R i t − s k j ) ⩽ [ t ] 1 , ∀ t ∈ [ 0 , T ] , ∀ j ∈ [ 1 , 7 ] , ∀ k ∈ [ 1 , 10 ] \begin{aligned} s.t.\left\{ \begin{aligned} %\nonumber &P_{s_j^7, s_2^0}=\begin{aligned}[t]0, &j \in[1,10]\\\end{aligned}\\ &P_{s_{j 1}^i, s_{j 2}^1}= \begin{aligned}[t] &\begin{cases}1 & , j 1-j 2 \in[1,0] \\ 0, & \text {, 其他 }\end{cases}, &\forall i \in[1,6]\\ \end{aligned}\\ &P_{s_{j 1}^7, s_{j 2}^{\top}}= \begin{aligned}[t] \begin{cases}1, & j 2-j, 1 \in[1,0] \\ 0, & \text { 其他 }\end{cases} \\ \end{aligned}\\ &P_{s_{j 1}^i, s_{j 2}^0}= \begin{aligned}[t] \begin{cases}1 & , j 1=1 \cap j 2=2 \\ 0, & \text {, 其他 }\end{cases}, &\forall i \in[1,6] \\ \end{aligned}\\ &P_{s_{j 1}^7, s_{j 2}^0}= \begin{aligned}[t] \begin{cases}1 & , j 1=10 \cap j 2=1 \\ 0 & , \text { 其他 }\end{cases} \\ \end{aligned}\\ &\sum_{i=1}^n\delta\left(R_i^t-s_1^0\right)\leqslant \begin{aligned}[t] 1, &\forall t \in[0, T] \\ \end{aligned}\\ &\sum_{i=1}^n\delta\left(R_i^t-s_2^0\right)\leqslant \begin{aligned}[t] 1, &\forall t \in[0, T] \\ \end{aligned}\\ &d_k= \begin{aligned}[t] 4, &\forall D_j^i \\ \end{aligned}\\ &s t_{l_i} > \begin{aligned}[t] n d_{l_{i-1}}, &\forall l_i \\ \end{aligned}\\ &\sum_{i=1}^n \delta\left(R_i^t-s_k^j\right) \leqslant \begin{aligned}[t] 1, &\forall t \in[0, T], \forall j \in[1,7], \forall k \in[1,10] \\ \end{aligned}\\ \end{aligned} \right. \end{aligned} s.t.⎩ ⎨ ⎧Psj7,s20=[t]0,j∈[1,10]Psj1i,sj21=[t]{10,,j1−j2∈[1,0], 其他 ,∀i∈[1,6]Psj17,sj2⊤=[t]{1,0,j2−j,1∈[1,0] 其他 Psj1i,sj20=[t]{10,,j1=1∩j2=2, 其他 ,∀i∈[1,6]Psj17,sj20=[t]{10,j1=10∩j2=1, 其他 i=1∑nδ(Rit−s10)⩽[t]1,∀t∈[0,T]i=1∑nδ(Rit−s20)⩽[t]1,∀t∈[0,T]dk=[t]4,∀Djistli>[t]ndli−1,∀lii=1∑nδ(Rit−skj)⩽[t]1,∀t∈[0,T],∀j∈[1,7],∀k∈[1,10]
5.2 算法描述
5.2.1 统计建模方法的改进
由于第二问去掉了约束6和7,于是,我们可以改进策略如下:
1. 接车横移机策略
接车横移机的决策树可以表示如下:
输入:u % 到达队列,PBS入口与返回车道10号位车辆到达顺序
输出:code
while 有车需要被调度 do
car=u.pop()
move21(car,type)
其中,move21()函数可以表示如下:
输入:car type
输出:code
if car.power == 燃油 then
if car.drive == 两驱 then
lane=3
else
lane=5
else
if car.drive == 两驱 then
lane=4
else
lane=2
if map(lane,10)==0 then % 目标车位闲置
code=lane+type*6
else if map(1,10)==0 then % 目标车位有车,停到备用车道1
code=1+type*6
else if map(6,10)==0 then
code=6+type*6
else
code=13 % 等待
2. 送车横移机策略
输入:u v n % 到达队列,每个车道1号位的车按到达顺序排列在此队列中 输出序列 剩余车辆数
输出:code
if 有车需要被调度 then
code=move22(u,v,n)
else
code=13
其中,move22()函数可以表示如下:
5.3 算例分析
相比问题一,问题二的时间得分都略有下降,本文认为是因为去掉约束6、7后,策略更倾向于考虑了局部的输出序列的得分作为优化目标,而忽视了车辆调度耗时所导致的。各算例求解如下所示。
5.4 附件一算例求解
| 指标 | 算法结果 |
|---|---|
| 总目标 | 9.8020 |
| 目标一 | -103 |
| 目标二 | 82 |
| 目标三 | 100 |
| 目标四 | 64.02 |
| 运行时间 | 267.652 |
5.5 附件二算例求解
| 指标 | 算法结果 |
|---|---|
| 总目标 | 32.7830 |
| 目标一 | -48 |
| 目标二 | 82 |
| 目标三 | 100 |
| 目标四 | 73.83 |
| 运行时间 | 289.703 |
6 模型评价与未来展望
6.1 模型评价
6.1.1 模型的优点
-
建立了整数优化模型,明确表达PBS约束条件,具体化调度过程;
-
证明了最短时间T的上界,明确求解域;
-
提出指令序列这一概念,将结果矩阵映射到一个低维流形中,极大减小求解复杂度;
-
针对数据特点,提出了有效的启发式规则,可以在短时间内得到高质量的结果,同时不受随机因素扰动,具有一定的鲁棒性,能够保证在相同条件下每次运行所得结果具有一致性。
6.1.2 模型的缺点
-
即使是压缩后的解空间,规模依然十分庞大,需要花费大量时间用于求解;
-
本文所设计的算法为启发式规则,未严格证明其为最优解。
本文代码:汽车制造涂装-总装缓存调序区调度优化建模: 【2022研究生数模 二等奖】汽车制造涂装-总装缓存调序区调度优化建模 (gitee.com)