数据库索引

索引

       

概念：

        索引是一种特殊的文件，包含着对数据表里所有记录的引用指针。可以对表中的一列或多列创建索引， 并指定索引的类型，各类索引有各自的数据结构实现。

 

作用：

        索引（目录）：提高查询效率， 可用于快速定位、检索数据。 提高数据库的性能。

何时用？

（1）数据量较大，且经常对这些列进行条件查询。

（2）该数据库表的插入操作，及对这些列的修改操作频率较低。

（3）索引会占用额外的磁盘空间。

    满足以上条件时，考虑对表中的这些字段创建索引，以提高查询效率

反之，如果非条件查询列，或经常做插入、修改操作，或磁盘空间不足时，不考虑创建索引。

索引付出代价：（缺点）

1.消耗更多空间

2.虽然提高了查找速率，但是降低了增删改的效率

    （插入新纪录，需要重新调整索引）

查询频率高于增删改，因此还是值得使用索引的

查看索引

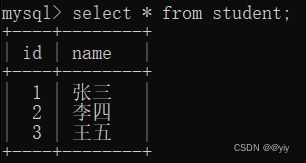
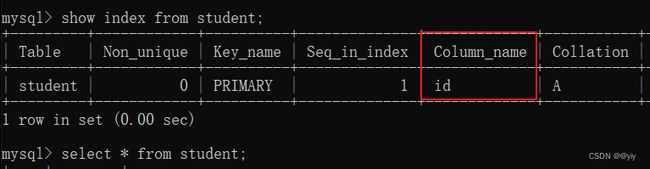
查看上述学生表索引

show index from student;

show index from 表名

创建索引（低效操作）

会创建一些相关的数据结构支持索引

create index index_sttudent_name on student(name);

creat index 索引名 on 表名（列名）

删除索引

drop index 索引名 on 表名;

 

索引背后的数据结构 

索引如何提高查询效率（背后的数据结构怎么样）

哈希表和二叉搜索树,都不太适合于做数据库的索引。

 

哈希表

（1） 哈希表适合进行精确查询，效率是最高的。 哈希表虽然增删改查时间复杂度为：O(1)

（2）不适合进行范围查询（ between ？and ？ 这类范围查询 ）和顺序查找（一个一个比对结果）

（3）会引发哈希冲突

 

二叉搜索树

（1）二叉搜索树会发生树倾斜,相当于退化成了一个链表，导致查询速度变慢, O(N) [最坏情况]

（2）AVL树/红黑树(比较平衡的二 叉搜索树) O(logN)， 如果数据库数据特别多, AVL树/红黑树 高度比较高. (logN)，由于一个节点只存储一条记录，所以一次查询可能会有多次磁盘IO，查询速度变慢。

树的高度较高时： 查询效率也会有所影响， 如果比较次数是在内存进行，多比几次，少比几次，都没事，内存上读写速度还是较快的。 但是如果每次比较要读硬盘（速度比内存慢的多），索引效率依赖于磁盘IO次数， 这样效率就会很低。 磁盘读写并不是按需读取，而是按页预读，一次会读一页的数据。

数据库索引量身定做的数据结构：B+树

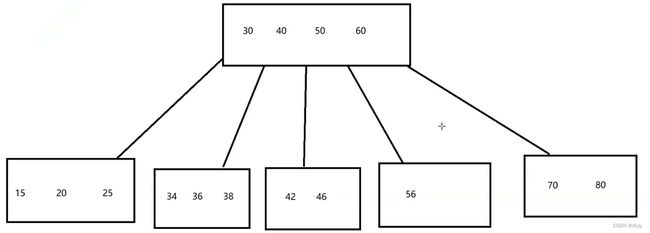
先认识B-树，再识B+树， B树是一个N叉搜索树

每个节点上，可能会包含N- 1个值，也可以更少。 N- 1个值就把区间划分成N份。

分成N个叉的意义 ：

    一个节点可以存储多条记录，因此同样元素的数据集合的时候,比二叉树的高度小很多. I/O次数也就降低了不 少。

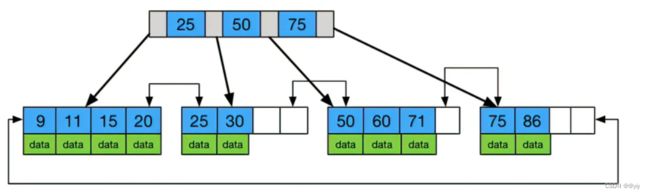
B+树

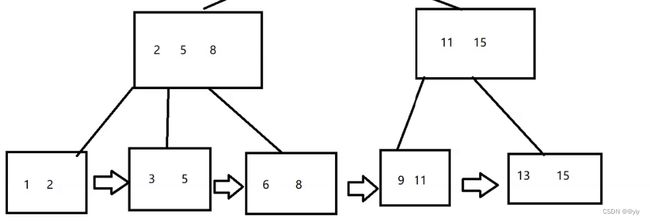
相对于B树，B+树叶子之间，增加了链表，获取所有节点，不再需要中序遍历。

（1）在叶子节点这里，已经是完整的数据集合。 前面非叶子节点的值，

         最终都会在叶子节点里体现出来。（非叶子结点并不存储真正的data）

（2）叶子结点为首尾相连的链表

 

B和B+树特点：

（1）B树中的值不会重复出现

         B+树值可能重复出现的

         (父元素的值,会在子元素中以最大值/最小值的姿态 出现)

（2）在叶子节点这里，B+树会把所有的叶子节点以链表的形式 首尾相连。

         这个时候就非常便于范围查找 id > 5  and  id < 10

（3）正因为叶子节点是全集数据,只需要把每一行

         (每一条记录的完整的所有 列关联到叶子节点上即可)，

          非叶子节点只需要保存索引列(只存个id )