AdaAffoord论文笔记
论文链接:https://arxiv.org/pdf/2112.00246.pdf
应用背景:
通过增加少量的机器臂和物体的快速交换,使得家庭辅助机器人知道如何正确打开关闭抽屉、柜子、开关等。
现有问题:
现有的方法没有发掘隐藏的运动学细节,如下图所示,当没有明确的门把手信息时,现有的方法会将可能的开启位置均匀化(图中(b)列的第一行所示,柜子的边缘的一周都标上差不多颜色,表示都有可能是开启的位置),但这个样子无法满足家庭辅助机器人的要求。

主要方法和创新点:
通过在测试时加入少量机械臂和物体的交互,使得机器人可以准确地感知正确的抓取位置和施力方向。
记物体为 O ∈ R N × 3 O\in \mathbb{R}^{N×3} O∈RN×3,输出的热图为 A ∈ [ 0 , 1 ] N A\in [0,1]^N A∈[0,1]N,热图上某位置的数字对应于该位置是有效抓取点的可能性大小,机械臂夹子的朝向使用 R i p ∈ S O ( 3 ) R_i^p\in SO(3) Rip∈SO(3)表示,其中 p p p为物体 O O O上的一点。 s i p ∈ [ 0 , 1 ] s_i^p\in[0,1] sip∈[0,1]表示对应的 R i p R_i^p Rip可以实现成功交互的可能性(具体说来,就是用机械臂的夹子夹住 p p p点,并且夹子朝向 R R R施力时可以正确完成,比如说打开柜子等任务的可能性大小)。记每一次的尝试为 I 1 = ( O i , p i , R i , m i ) I_1=(O_i, p_i, R_i, m_i) I1=(Oi,pi,Ri,mi),这里 m i m_i mi表示在用机械臂的夹子夹住物体 O I O_I OI上 p i p_i pi点,并且夹子朝向 R i R_i Ri施力时,物体的状态该变量,比如说抽屉被拉出来多少距离,柜子打开多少角度等。从而构成交互(这里的交互就是指每一次尝试,包括选择抓取点和施力方向)序列 I = { I 1 , I 2 , ⋯ } \mathcal{I}=\{I_1, I_2, \cdots\} I={I1,I2,⋯}。一开始的初始化热图 A A A是由Where2Act网络(现有的工作)预测得到的,在经过 I \mathcal{I} I中的交互后的,得到的热图记为 A I ∈ [ 0 , 1 ] N A_{\mathcal{I}}\in [0,1]^N AI∈[0,1]N。同样, s i p s_i^p sip更新为 s i , I p s_{i,\mathcal{I}}^p si,Ip。
架构
主要由AIP(Adaptive Interaction Proposal)和APP(Adaptive Affordance Prediction)两部分构成。AIP的主要目的是生成少量有效的交互方式,即生成 I {\mathcal{I}} I,AAP的主要作用的预测 A I A_{\mathcal{I}} AI。
测试阶段
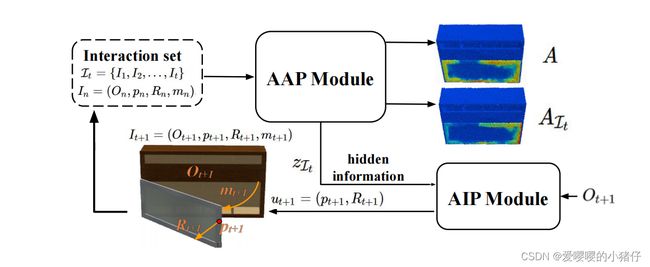
如下图所示,首先根据Where2Act网络预测的热图 A A A,AIP生成第一次的交互 I 1 I_1 I1,送入到AAP中,以此类推,在第t次过程中,生成的交互为 I t I_t It,到目前为止一共进行了 I t = { I 1 , ⋯ , I t } \mathcal{I}_t=\{I_1,\cdots,I_t\} It={I1,⋯,It}次交互,将 I t \mathcal{I}_t It作为输入,送入到APP中,可以得到隐藏信息 z I t ∈ R 128 z_{\mathcal{I}_t}\in \mathbb{R^{128}} zIt∈R128。AIP以 z I t z_{\mathcal{I}_t} zIt为输入,得到了 t + 1 t+1 t+1时刻的行动 u t + 1 = ( p t + 1 , R t + 1 ) u_{t+1}=(p_{t+1},R_{t+1}) ut+1=(pt+1,Rt+1)。执行完 u t + 1 u_{t+1} ut+1后,即可得到 t + 1 t+1 t+1时刻的交互信息 I t + 1 ← I t + 1 ∪ { I t + 1 } \mathcal{I}_{t+1}\gets \mathcal{I}_{t+1}\cup\{I_{t+1}\} It+1←It+1∪{It+1}。这个过程迭代执行,直到交互时间结束或者AIP模块觉得交互可以结束,迭代结束。假设迭代结束在 T T T时刻,则最终的热图 A I = A I t A_{\mathcal{I}}=A_{\mathcal{I}_t} AI=AIt。
输入解码器
如下图所示,清晰地展示了每个模块的输入是什么。本文中,使用了PointNet++分割网络将输入的点云 O ∈ R N × 3 O\in\mathbb{R}^{N×3} O∈RN×3编码成特征图 f O ∈ R N × 128 f_O\in\mathbb{R}^{N×128} fO∈RN×128,记 p ∈ O p\in O p∈O点的特征为 f p ∣ O ∈ R N × 128 f_{p|O}\in\mathbb{R}^{N×128} fp∣O∈RN×128。使用MLP将其他输入向量均编译为128维,记为 f a ∈ R 128 f_a\in\mathbb{R}^{128} fa∈R128。然后将 f p ∣ O f_{p|O} fp∣O和 f a f_a fa结合起来构成 f I ∈ R 256 f_I\in\mathbb{R}^{256} fI∈R256。不同的编码器之间不共享权重。

AAP
AAP的主要作用是以 I \mathcal{I} I为输入,得到 A I A_{\mathcal{I}} AI。如上图所示,AAP主要由 E A A P \mathcal{E}_{AAP} EAAP、 C A A P \mathcal{C}_{AAP} CAAP和 D A A P \mathcal{D}_{AAP} DAAP构成。
E A A P \mathcal{E}_{AAP} EAAP主要通过输入 I \mathcal{I} I,使用之前提到的编码器(MLP),将其转化为128维的向量,再使用一个MLP得到隐藏信息 z I z_{\mathcal{I}} zI(简记为 z z z)。由于 I \mathcal{I} I由多个 I I I构成,所以额外使用一个MLP来预测不同 I I I的权重,最终的 z I z_{\mathcal{I}} zI可以表示为 z I ← ( ∑ i z I i × w I i ) / ( ∑ i w I i ) z_{\mathcal{I}}\gets (\sum_iz_{I_i}×w_{I_i})/(\sum_i w_{I_i}) zI←(∑izIi×wIi)/(∑iwIi)。
C A A P \mathcal{C}_{AAP} CAAP的输入为 u = ( p , R ) u=(p,R) u=(p,R)和 z z z,得到 s u ∣ z A A P ∈ [ 0 , 1 ] s_{u|z}^{AAP\in [0,1]} su∣zAAP∈[0,1],即该操作完成任务的可能性。
D A A P \mathcal{D}_{AAP} DAAP的输入为 O O O和 p p p,得到 a p ∣ z A A P ∈ [ 0 , 1 ] a_{p|z}^{AAP\in [0,1]} ap∣zAAP∈[0,1],即 p p p点是有效的可交互点的可能性。
这边有个疑问:既然 C A A P \mathcal{C}_{AAP} CAAP处理的的 u u u中包含了 p p p,为什么还需要一个 D A A P \mathcal{D}_{AAP} DAAP。
AIP
AIP主要由 C A I P \mathcal{C}_{AIP} CAIP和 D A I P \mathcal{D}_{AIP} DAIP构成。
C A I P \mathcal{C}_{AIP} CAIP的输入为 { O , p , R , s u ∣ z A A P , z } \{O,p,R,s_{u|z}^{AAP},z\} {O,p,R,su∣zAAP,z},得到 s u ∣ z A I P s_{u|z}^{AIP} su∣zAIP,即 u u u操作能发掘多少有效的未知信息。
D A I P \mathcal{D}_{AIP} DAIP的输入为 { O , p , R , a p ∣ z A A P , z } \{O,p,R,a_{p|z}^{AAP},z\} {O,p,R,ap∣zAAP,z},得到 a p ∣ z A I P a_{p|z}^{AIP} ap∣zAIP,即 p p p点能发掘多少有效的未知信息。
AIP的运行流程是:首先由APP得到 z z z,然后通过 D A I P \mathcal{D}_{AIP} DAIP得到最具潜力的探索点 p p p( a p ∣ z A I P a_{p|z}^{AIP} ap∣zAIP得分最高的点),然后就该点随机采样100种操作 { u 1 , u 2 , ⋯ , u 100 } \{u_1, u_2,\cdots,u_{100}\} {u1,u2,⋯,u100},然后选择 s u ∣ z A A P s_{u|z}^{AAP} su∣zAAP分数最高的 u u u,执行该操作。
当时间到了,或者AIP认为没有什么有潜力的探索时,结束交互。
训练及损失
C A A P \mathcal{C}_{AAP} CAAP的训练使用交叉熵函数:
L C A A P = − 1 B ∑ i r i log ( s u i ∣ z A A P ) + ( 1 − r i ) log ( 1 − s u i ∣ z A A P ) \mathcal{L}_{\mathcal{C}}^{AAP}=-\frac{1}{B}\sum_i ri\log(s_{u_i|z}^{AAP})+(1-r_i)\log(1-s_{u_i|z}^{AAP}) LCAAP=−B1i∑rilog(sui∣zAAP)+(1−ri)log(1−sui∣zAAP)
其中,如果 m i > τ m_i>\tau mi>τ,则 r i = 1 r_i=1 ri=1,否则 r i = 0 r_i=0 ri=0。简单说来,就是当 m i m_i mi比较大的时候,也就是说操作 u i u_i ui带来了比较好的结果,比如说把抽屉拉了比较远,或者柜子开的比较大,那么 u i u_i ui对应的 s u i ∣ z A A P s_{u_i|z}^{AAP} sui∣zAAP的值也应该越大,表示该操作更有可能完成预设的任务。
D A A P \mathcal{D}_{AAP} DAAP的训练采用 L 1 \mathcal{L_1} L1损失, a p ∣ z A A P a_{p|z}^{AAP} ap∣zAAP真值通过下面的方式获得:首先针对 p p p点,使用Where2Act随机产生100个操作 u u u,然后使用 C A A P \mathcal{C}_{AAP} CAAP(应该是已经训练好的)来产生 s u ∣ z A A P s_{u|z}^{AAP} su∣zAAP,然后使用五个最高得分的 s u ∣ z A A P s_{u|z}^{AAP} su∣zAAP的均值作为 a p ∣ z A A P a_{p|z}^{AAP} ap∣zAAP的真值。
C A I P \mathcal{C}_{AIP} CAIP的训练采用 L 1 \mathcal{L_1} L1损失, s u ∣ z A I P s_{u|z}^{AIP} su∣zAIP真值通过下面的方式获得:给定一些列的交互 I T = { I 1 , I 2 , ⋯ } \mathcal{I}_{\mathcal{T}}=\{I_1, I_2, \cdots\} IT={I1,I2,⋯},选取其的两个子集 I i − 1 = { I 1 , I 2 , ⋯ , I i − 1 } \mathcal{I}_{i-1}=\{I_1,I_2,\cdots,I_{i-1}\} Ii−1={I1,I2,⋯,Ii−1}和 I i = { I 1 , I 2 , ⋯ , I i } \mathcal{I}_{i}=\{I_1,I_2,\cdots,I_{i}\} Ii={I1,I2,⋯,Ii},通过 E A A P \mathcal{E}_{AAP} EAAP得到其对应的特征 z I i z_{\mathcal{I}_{i}} zIi和 z I i − 1 z_{\mathcal{I}_{i-1}} zIi−1。然后将 z I i z_{\mathcal{I}_{i}} zIi和 z I i − 1 z_{\mathcal{I}_{i-1}} zIi−1分别输入到 C A A P \mathcal{C}_{AAP} CAAP中,并且计算两者的差,作为 s u 1 ∣ z I i − 1 A I P s_{u_1|z_{\mathcal{I}_{i-1}}}^{AIP} su1∣zIi−1AIP的真值 g t u i ∣ z I i − 1 A I P gt_{u_i|z_{\mathcal{I}_{i-1}}}^{AIP} gtui∣zIi−1AIP,也就说多进行了一步 u i u_i ui,可以给 C A A P \mathcal{C}_{AAP} CAAP带来多大的变化。也就是鼓励发掘给 C A A P \mathcal{C}_{AAP} CAAP带来更多变化的操作 u i u_i ui。
D A I P \mathcal{D}_{AIP} DAIP的训练采用另一种 L 1 \mathcal{L_1} L1损失,和 D A A P \mathcal{D}_{AAP} DAAP的训练类似, a p ∣ z A I P a_{p|z}^{AIP} ap∣zAIP真值通过下面的方式获得:首先针对 p p p点,使用Where2Act随机产生100个操作 u u u,然后使用 C A I P \mathcal{C}_{AIP} CAIP(应该是已经训练好的)来产生 s u ∣ z A I P s_{u|z}^{AIP} su∣zAIP,然后使用五个最高得分的 s u ∣ z A I P s_{u|z}^{AIP} su∣zAIP的均值作为 a p ∣ z A I P a_{p|z}^{AIP} ap∣zAIP的真值。
训练过程采取迭代训练的方式,首先用随机生成的交互训练AAP,然后训练AIP生成更加有效和高效的操作 u u u。然后使用训练好的AIP来微调AAP。训练交换训练过程直到两个模块趋同。

