算法通关村第十七关——贪心高频问题（白银）

1 区间问题

1.1 判断区间是否重叠

leetcode 252.会议室(要会员，md)

给定一个会议时间安排的数组 intervals ，每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ，请你判断一个人是否能够参加这里面的全部会议。

示例 1:
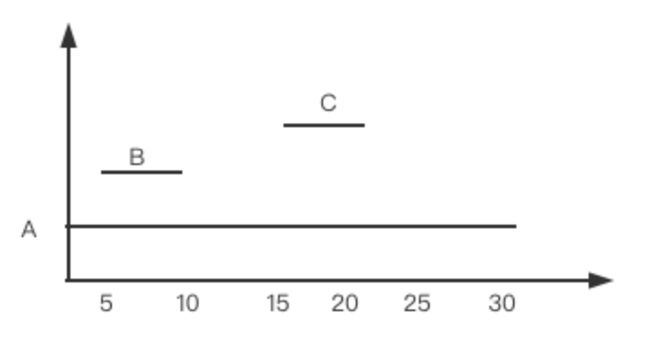
输入: intervals = [[0,30],[15,20],[5,10]]
解释: 存在重叠区间，一个人在同一时刻只能参加一个会议。

因为一个人在同一时刻只能参加一个会议，因此题目实质是判断是否存在重叠区间，将区间按照会议开始时间进行排序，然后遍历一遍判断后面的会议开始的时候是否前面的还没有结束即可。也就是上图中如果出现重叠的部分就直接返回false即可。

public boolean canAttendMeetings(int[][] intervals) {
     // 将区间按照会议开始实现升序排序
     Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
     // 遍历会议，如果下一个会议在前一个会议结束之前就开始了，返回 false。
     for (int i = 1; i < intervals.length; i++) {
         if (intervals[i][0] < intervals[i - 1][1]) {
         	return false;
         }
     }
     return true;
 }

1.2 合并区间

leetcode 56. 合并区间

跟上道题有点像，但还是有区别

思路：

• 什么情况下区间重叠？
• 怎么将新的区间进行保存？

所以一样的套路，先排序，让所有的相邻区间尽可能的重叠在一起，按左边界，或者右边界排序都可以，处理逻辑稍有不同。

按照左边界从小到大排序之后，如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。

所以，合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

class Solution {
    public int[][] merge(int[][] intervals) {
        List<int[]> res = new LinkedList<>();
        //按照左边界排序
        Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
        //initial start 是最小左边界
        int start = intervals[0][0];
        int rightmostRightBound = intervals[0][1];
        for (int i = 1; i < intervals.length; i++) {
            //如果左边界大于最大右边界
            if (intervals[i][0] > rightmostRightBound) {
                //加入区间 并且更新start
                res.add(new int[]{start, rightmostRightBound});
                start = intervals[i][0];
                rightmostRightBound = intervals[i][1];
            } else {
                //更新最大右边界
                rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
            }
        }
        res.add(new int[]{start, rightmostRightBound});
        return res.toArray(new int[res.size()][]);
    }
}

1.3 插入区间

leetcode 57. 插入区间

本题就是上一题的再拓展，本题中的区间已经按照起始端点升序排列，因此我们直接遍历区间列表，寻找新区间的插入位置即可。具体步骤如下：

1. 首先将新区间左边且相离的区间加入结果集（遍历时，如果当前区间的结束位置小于新区间的开始位置，说明当前区间在新区间的左边且相离）；

2. 接着判断当前区间是否与新区间重叠，重叠的话就进行合并，直到遍历到当前区间在新区间的右边且相离，将最终合并后的新区间加入结果集；

3. 最后将新区间右边且相离的区间加入结果集。

   这就不画图了，直接把newInterval添加到res[idx++]的位置，在进行while

class Solution {
    public int[][] insert(int[][] intervals, int[] newInterval) {
        int[][] res = new int[intervals.length + 1][2];
        int idx = 0;
        int i = 0;
        // 遍历区间列表：
        // 首先将新区间左边且相离的区间加入结果集
        while(i < intervals.length && intervals[i][1] < newInterval[0]){
            res[idx++] = intervals[i++];
        }
        // 判断当前区间是否与新区间重叠，重叠的话就进行合并，直到遍历到当前区间在新区间的右边且相离，
        // 将最终合并后的新区间加入结果集
        while(i < intervals.length && intervals[i][0] <= newInterval[1]){
            newInterval[0] = Math.min(intervals[i][0], newInterval[0]);
            newInterval[1] = Math.min(intervals[i][1], newInterval[1]);
            i++;
        }
        res[idx++] = newInterval;
        // 最后将新区间右边且相离的区间加入结果集
        while (i < intervals.length) {
            res[idx++] = intervals[i++];
        }
        return Arrays.copyOf(res, idx);
    }
}

2 划分字母区间

leetcode 763. 划分字母区间

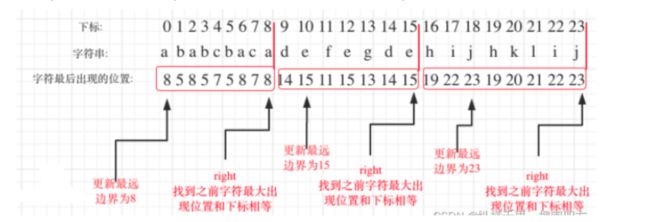
该遍历过程相当要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。所以可以这么做：

• 首先，统计每一个字符最后出现的位置

• 然后，从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点。

代码：

class Solution {
    public List<Integer> partitionLabels(String s) {
        List<Integer> res = new LinkedList<>();
        int[] edge = new int[26];
        char[] chars = s.toCharArray();
        // 记录每个字母最后一次出现的位置
        for(int i=0; i < chars.length; i++){
            edge[chars[i] - 'a'] = i;
        }
        int idx = 0;
        // 记录上一个子串的结束位置
        int last = -1;
        for(int i = 0; i < chars.length; i++){
            idx = Math.max(idx, edge[chars[i] - 'a']);
            // 当遍历到当前位置等于当前最大边界时，将当前子串长度加入结果列表
            if(i == idx){
                res.add(i - last);
                last = i;
            }
        }
        return res;
    }
}

3 加油站问题

leetcode 134. 加油站

代码随想录详解

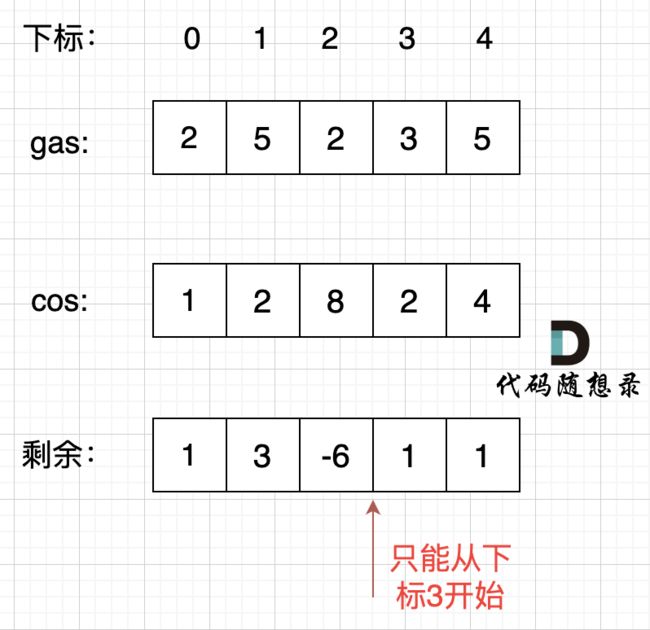
示例给的两个数组只是代表从当前站可以提供多少油料，以及从前一个位置过来需要消耗多少油料，因为是环。所以这里gas[0]=1和cost[0]=3就表示第一个站有1升汽油，从第一个站到第二个站需要消耗3升汽油。

很显然在第一个站只能加1升汽油，但是从第一到第二个站需要消耗3升汽油，因此不能从第一个站开始走。

解法一：

暴力解法（略）

解法二：贪心（全局最优解）

直接从全局进行贪心选择，情况如下：

• 情况一：如果gas的总和小于cost总和，那么无论从哪里出发，一定是跑不了一圈的
• 情况二：rest[i] = gas[i]-cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。
• 情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能把这个负数填平，能把这个负数填平的节点就是出发节点。

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int sum = 0;
        int min = 0;
        for (int i = 0; i < gas.length; i++) {
            sum += (gas[i] - cost[i]);
            min = Math.min(sum, min);
        }

        if (sum < 0) return -1;
        if (min >= 0) return 0;

        for (int i = gas.length - 1; i > 0; i--) {
            min += (gas[i] - cost[i]);
            if (min >= 0) return i;
        }

        return -1;
    }
}

这种算法实话应该不属于贪心算法

解法三：贪心（局部最优解）

• 可以换一个思路，首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。

• 每个加油站的剩余量rest[i]为gas[i] - cost[i]。

• i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

那么为什么一旦[0，i] 区间和为负数，起始位置就可以是i+1呢，i+1后面就不会出现更大的负数？

如果出现更大的负数，就是更新i，那么起始位置又变成新的i+1了。

那有没有可能 [0，i] 区间 选某一个作为起点，累加到 i这里 curSum是不会小于零呢？ 如图：

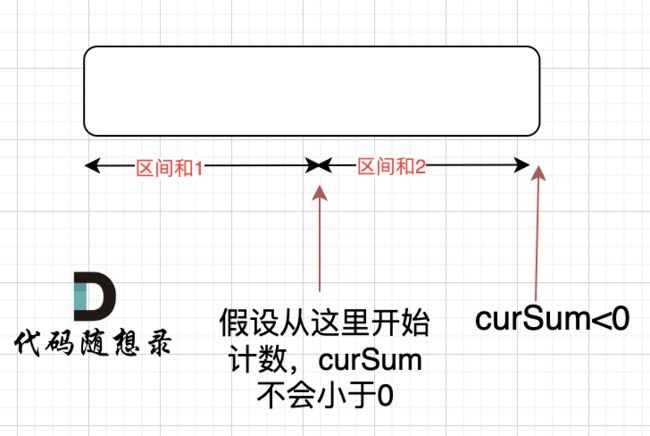
如果 curSum<0 说明 区间和1 + 区间和2 < 0， 那么 假设从上图中的位置开始计数curSum不会小于0的话，就是 区间和2>0。

区间和1 + 区间和2 < 0 同时 区间和2>0，只能说明区间和1 < 0， 那么就会从假设的箭头初就开始从新选择其实位置了。

那么局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。

局部最优可以推出全局最优，找不出反例，试试贪心！

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int curSum = 0;
        int totalSum = 0;
        int index = 0;
        for (int i = 0; i < gas.length; i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {
                index = (i + 1) % gas.length ; 
                curSum = 0;
            }
        }
        if (totalSum < 0) return -1;
        return index;
    }
}

over~~