融合鱼鹰和柯西变异的麻雀优化算法，效果好的起飞！改进麻雀，力荐！

经常有小伙伴后台留言问：

作者改进的算法可不可以用来写论文呀？

回答是：当然可以！

如果我的文章能帮助到大家写论文，那是作者的荣幸呀！

今天为大家带来的这期融合鱼鹰和柯西变异的麻雀优化(Osprey-Cauchy-Sparrow Search Algorithm,OCSSA)算法，效果直接完爆蜣螂、麻雀、减法优化器等优秀的算法，而且同样不会增加算法的复杂度，在主循环中，只调用了一次适应度函数，因此可以用于复杂工程的优化。运行时间不会像某些加入了反向学习、贪婪策略等改进算法一样陡然上升。

在麻雀算法的基础上，改进点如下：

①采用Logistic混沌映射，初始化种群的多样性。

②采用鱼鹰优化算法在第一阶段的全局勘探策略替换原始麻雀算法的探索者位置更新公式。鱼鹰优化算法可以弥补麻雀算法过分依赖于上一代麻雀位置的更新方式，采用随机检测其中一个食物的位置并攻击它。基于鱼鹰向鱼的运动模拟方式来更新麻雀算法中探索者的位置更新方式。鱼鹰优化算法在第一阶段的全局勘探策略公式如下：

③采用柯西变异策略替换原始麻雀算法的跟随者位置更新公式。柯西分布与标准的正态分布相似，为连续的概率分布，在原点处值较小，两端较为扁长，逼近零速率较慢， 因而相比于正态分布能产生更大的扰动。因此，利用柯西变异对麻雀位置更新中的个体进行扰动，从而扩大麻雀算法的搜索规模，进而提升算法跳出局部最优能力。

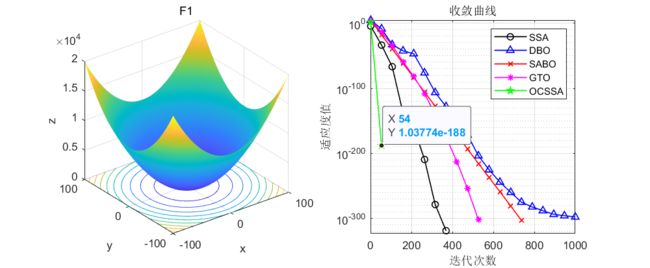
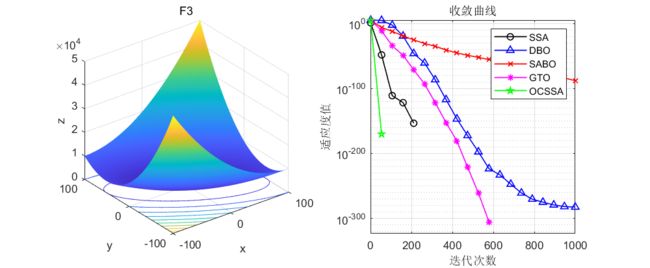
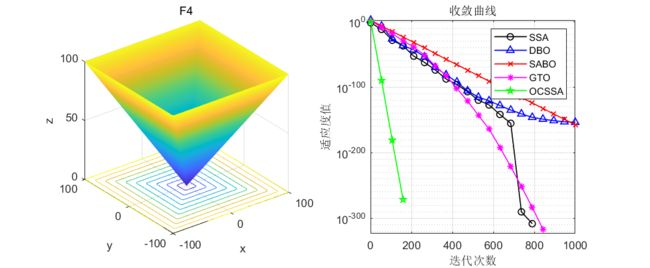
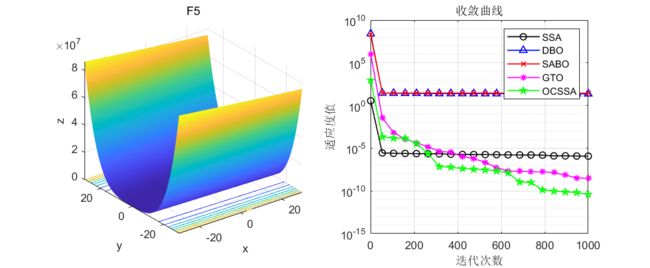
在CEC2005函数集上进行测试，结果如下：其中OCSSA为本文所提改进算法，SSA是原始的麻雀优化算法，DBO是蜣螂优化算法，SABO是减法平均优化器算法，GTO是人工大猩猩部队优化算法。

算法迭代1000次，每种算法的粒子数设置为100。

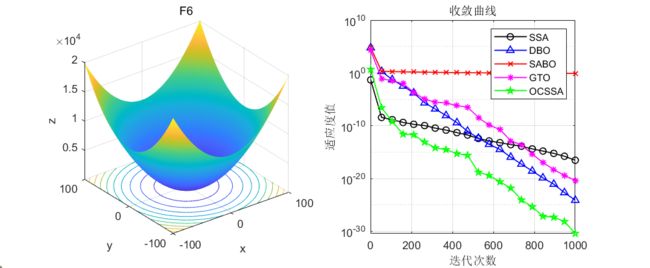
CEC2005测试效果

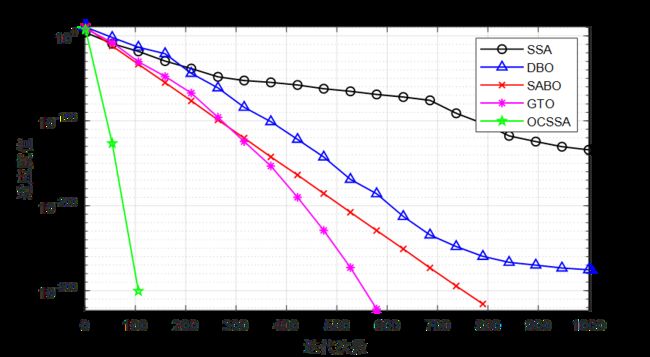
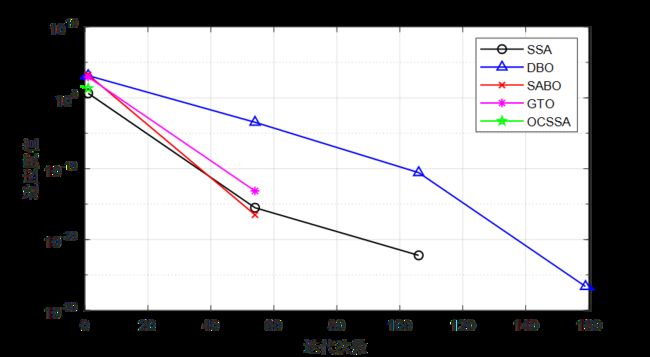
CEC2021测试效果

友情提示：如果发现曲线图中，某些legend只有一个点，例如CEC2021测试集的F3函数，那证明这个算法收敛速度极快，在前期就收敛到0了！

结果分析：在单峰值函数与多峰值函数的测试中可以看到，融合鱼鹰和柯西变异的麻雀优化的麻雀算法寻优效果是真的好！

代码展示

clear
clc
close all
dim = 20; % 维度，可选 10, 20
number= 9;  % 函数名：1 - 10
[lower_bound,upper_bound,variables_no,fobj] = Get_Functions_cec2021(number,dim);
% [lower_bound,upper_bound,variables_no,fobj]=CEC2005(number);  % [lb,ub,D,y]：下界、上界、维度、目标函数表达式
pop_size=50;                      % population members 
max_iter=1000;                  % maximum number of iteration
%% OOA
[DBO_Best_score,Best_pos,DBO_curve]=DBO(pop_size,max_iter,lower_bound,upper_bound,variables_no,fobj);  % Calculating the solution of the given problem using OOA 
display(['The best optimal value of the objective funciton found by DBO  for ' [num2str(number)],'  is : ', num2str(DBO_Best_score)]);
%% GTO
[GTO_Best_score,~,GTO_curve]=GTO(pop_size,max_iter,lower_bound,upper_bound,variables_no,fobj);
display(['The best optimal value of the objective funciton found by GTO  for ' [num2str(number)],'  is : ', num2str(GTO_Best_score)]);
%% SSA
[SSA_Best_score,~,SSA_curve]=SSA(pop_size,max_iter,lower_bound,upper_bound,variables_no,fobj);
display(['The best optimal value of the objective funciton found by SSA  for ' [num2str(number)],'  is : ', num2str(SSA_Best_score)]);
%% SABO
[SABO_Best_score,~,SABO_curve]=SABO(pop_size,max_iter,lower_bound,upper_bound,variables_no,fobj);
display(['The best optimal value of the objective funciton found by SABO  for ' [num2str(number)],'  is : ', num2str(SABO_Best_score)]);
%% OCSSA
[OCSSA_Best_score,~,OCSSA_curve]=OCSSA(pop_size,max_iter,lower_bound,upper_bound,variables_no,fobj);
display(['The best optimal value of the objective funciton found by OCSSA  for ' [num2str(number)],'  is : ', num2str(OCSSA_Best_score)]);
 %% Figure
figure
CNT=20;
k=round(linspace(1,max_iter,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:max_iter;
   semilogy(iter(k),SSA_curve(k),'k-o','linewidth',1);
    hold on
    semilogy(iter(k),DBO_curve(k),'b-^','linewidth',1);
    hold on
    semilogy(iter(k),SABO_curve(k),'r-x','linewidth',1);
    hold on
    semilogy(iter(k),GTO_curve(k),'m-*','linewidth',1);
    hold on
    semilogy(iter(k),OCSSA_curve(k),'g-p','linewidth',1);
grid on;
title(['F',num2str(number),'收敛曲线'])
xlabel('迭代次数');
ylabel('适应度值');
box on
legend('SSA','DBO','SABO','GTO','OCSSA')
set (gcf,'position', [300,300,600,330]

完整代码获取方式，后台回复关键词。关键词：

OCSSA