数据结构顺序表

线性表

线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串…
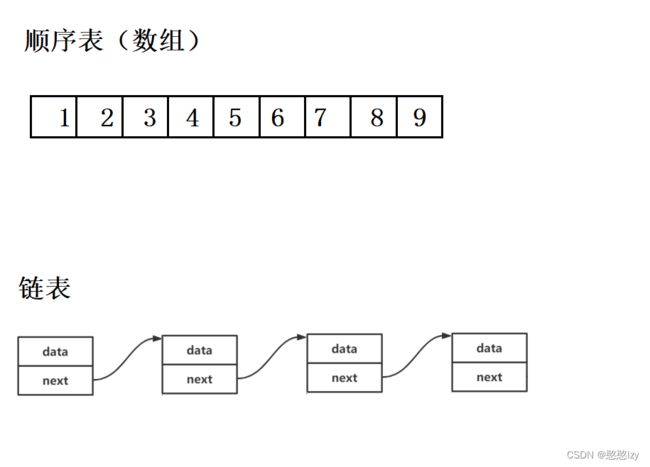
线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，
线性表在物理上存储时，通常以数组和链式结构的形式存储。

顺序表

概念及结构

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存
储。在数组上完成数据的增删查改。

顺序表一般可以分为：

• 静态顺序表：使用定长数组存储元素。

#define N 100 //用宏定义数组的长度
struct SeqList //顺序表 sequence list
{
   SLDataType a[N];//定长数组
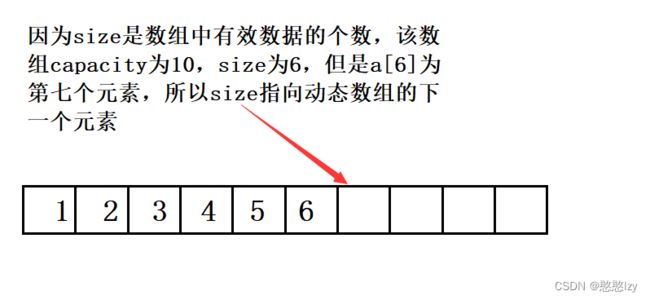
   int size; //有效数据的个数
};

• 动态顺序表:使用动态开辟的数组存储。

typedef struct SeqList
{
	SLDataType* a;//指向动态开辟的数组
	int size;//有效数据
	int capacity;//空间容量
}SL;

接口实现
静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了，空
间开多了浪费，开少了不够用。所以现实中基本都是使用动态顺序表，根据需要动态的分配空间
大小，所以下面我们实现动态顺序表。

头文件SeqList.h

#include
#include
#include

#define CAPACITY_INIT 5 //最初最大容量为5 

typedef int SLDataType;//定义动态顺序表的数据类型

typedef struct SeqList
{
	int size;//有效数据
	int capacity;//最大容量
	SLDataType* a;
}SL;//结构体类型为SL

一些函数的声明：

void SeqListInit(SL* pc);//顺序表的初始化

void SeqListDestory(SL* pc);//顺序表的销毁

void SeqListPrint(SL* pc);//顺序表的打印

void SeqListPushFront(SL* pc, SLDataType x);//头插

void SeqListPushBack(SL* pc, SLDataType x);//尾插

void SeqListPopFront(SL* pc);//头删

void SeqListPopBack(SL* pc);//尾删

void SeqListChackCapacity(SL* pc);//检查是否需要扩容

void SeqListInsert(SL* pc,int pos,SLDataType x);//在指定位置插入

void SeqListErse(SL* pc,int pos);//删除指定位置

int SeqListFind(SL* pc, SLDataType x);//查找

SeqList.c 文件中是一些函数的实现

顺序表的初始化：

void SeqListInit(SL* pc)//顺序表的初始化
{
	assert(pc);//断言
	pc->size = 0;//初始数据为0个
	pc->capacity = CAPACITY_INIT;//初始定义一个结构体容量
	pc->a = (SL*)malloc(sizeof(SLDataType) * pc->capacity);//开辟空间
	if (NULL == pc->a)
	{
		perror("malloc fail");
		return;
	}
}

顺序表的销毁

因为动态开辟的空间若不释放会造成空间浪费的

void SeqListDestory(SL* pc)//顺序表的销毁
{
	assert(pc);//断言
	free(pc->a);//释放
	pc->a = NULL;//置空防止也只针的生成
	pc->size = pc->capacity = 0;
}

顺序表的打印

void SeqListPrint(SL* pc)//顺序表的打印
{
	assert(pc);//断言

	for (int i = 0; i < pc->size; i++)
	{
		printf("%d ", pc->a[i]);
	}
	printf("\n");
}

检查数组是否需要扩容

void SeqListChackCapacity(SL* pc)//检查是否需要扩容
{
	assert(pc);//断言

	//判断是否需要扩容
//因为检查扩容只有在增加 头插 尾插 函数中使用，然后这些函数都是对单个数据的操作，size的设定本来就比capacity小，所以只需要当size等于capacity的时候就需要扩容
	if (pc->size == pc->capacity)//因为检查扩容只有在增加 头插 尾插 函数中使用，然后这些函数都是对单个数据的操作，size的设定本来就比capacity小，所以只需要当size等于capacity的时候就需要扩容
	{
		SLDataType* temp = realloc(pc->a, sizeof(SLDataType) * pc->capacity * 2);//一般扩容为二倍
		if (NULL == temp)
		{
			perror("realloc fail");
			return;
		}
		pc->a = temp;//realloc若后面的空间足够则会直接再pc->a的后面开辟空间，若后面空间不够的话会在内存中在找一块空间开辟
		//这时候原来的pc->a指向的就不是想要的这个动态空间了所以需要将temp的值赋给pc->a
		temp = NULL;//置空防止也只针的生成
		printf("扩容成功\n");//扩容成功提示一下
	}
}

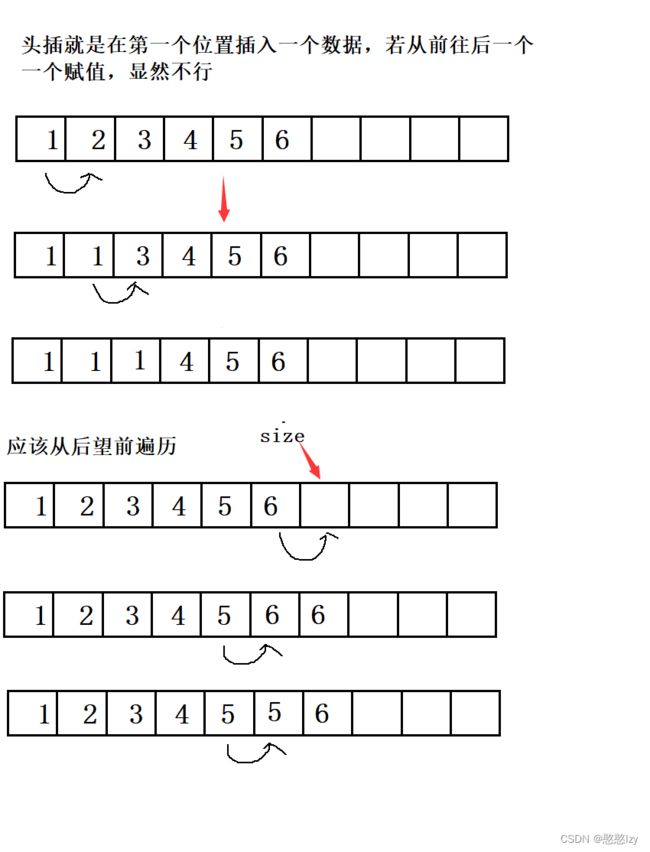
头插

图解：

原理明白了直接上代码：

void SeqListPushFront(SL* pc, SLDataType x)//头插
{
	assert(pc);//断言
	SeqListChackCapacity(pc);//判断是否需要扩容
	int end = pc->size;//定义end为顺序表后面一个数据的下标
	while (end)
	{
		pc->a[end] = pc->a[end - 1];
		end--;
	}
	pc->a[end] = x;//循环完end为0，这时候将需要插入的数据放在a[0]处
	pc->size++;//插入一个数据后size要自增1，size为有效数组的个数

}

尾插

void SeqListPushBack(SL* pc, SLDataType x)//尾插
{
	assert(pc);
	SeqListChackCapacity(pc);//检查内存是否需要扩容
	//因为size是数据的下一个的下标
	pc->a[pc->size++] = x;
}

头删

头删比较简单，只要后从前往后遍历，将后一个元素把前一个元素覆盖就好了

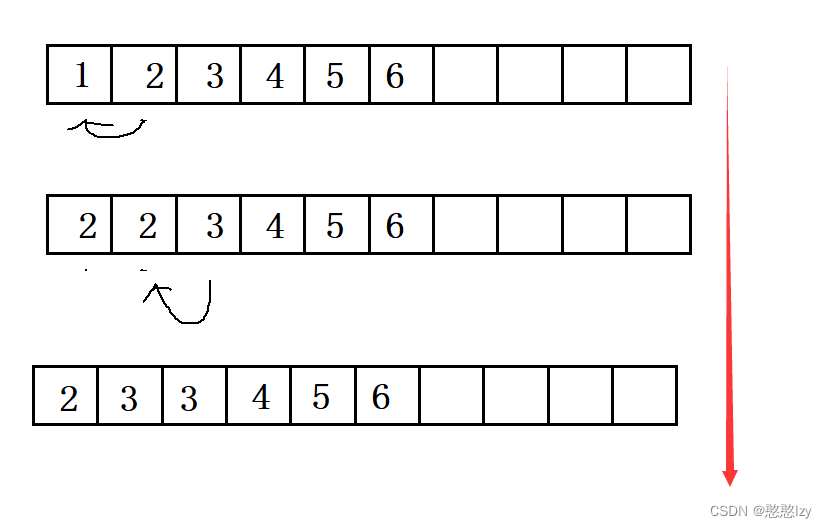
void SeqListPopFront(SL* pc)//头删
{
	assert(pc);
	assert(pc->size > 0);
	for (int i = 1; i < pc->size; i++)
	{
		pc->a[i - 1] = pc->a[i];
	}
	pc->size--;
	//pc->a[size]=0;//这里不需将原来数组的最后一个置为0，因为你不确定原来的数据是多少，万一为0呢，那么这毫无意义，size为有效数据的个数，只要操作数组a时，用size来限制就可以了
}

尾删

尾删看似简单但是有坑，你是不是认为将size自减1就ok了，大体思路是这样的，但是若数组中有3个数据，但是你执行了4次尾删，那么size就会为-1，这时候在对数组进行使用时，就会造成数组越界，所以我们要对size进行限制

void SeqListPopBack(SL* pc)//尾删
{
	assert(pc);//断言
	//暴力检查
	assert(pc->size > 0);//断言的括号中为真就执行过去，啥也不发生，若为假，那么就会使程序结束
	pc->size--;
}

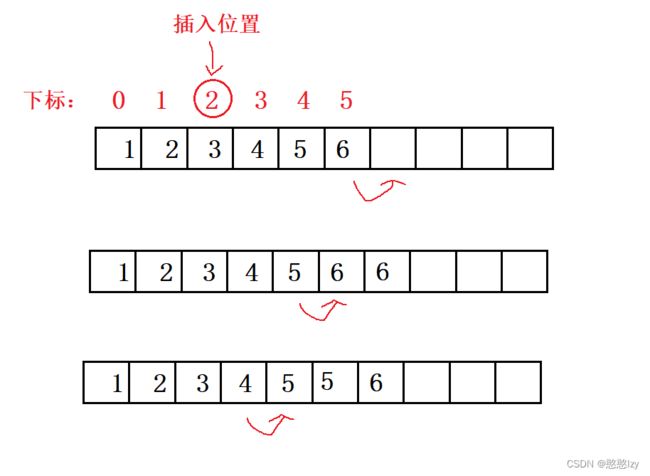
插入（指定任意位置）

原理和头插差不多

上代码：

void SeqListInsert(SL* pc,int pos, SLDataType x)//插入
{
	assert(pc);
	SeqListChackCapacity(pc);//判断是否需要扩容
	int end = pc->size;//size为顺序表后面一个数据单位的下标
	while (end>pos)//end等于pos+1时调用最后一次循环，将pos位置的数据赋值到后一位了
	{
		pc->a[end] = pc->a[end-1];
		end--;
	}
	pc->a[pos] = x;//将要插入的数据放入指定位置
	pc->size++;//插入数据后size要自增一

}

利用插入函数可以实现头插尾插
头插

void SeqListPushFront(SL* pc, SLDataType x)//头插
{
	SeqListInsert(pc,0,x);
}

尾插

void SeqListPushBack(SL* pc, SLDataType x)//尾插
{
	SeqListInsert(pc,pc->size,x);
}

删除（指定位置）

和头删原理相同，但是只要删除就要考虑size的范围，不能使数组越界

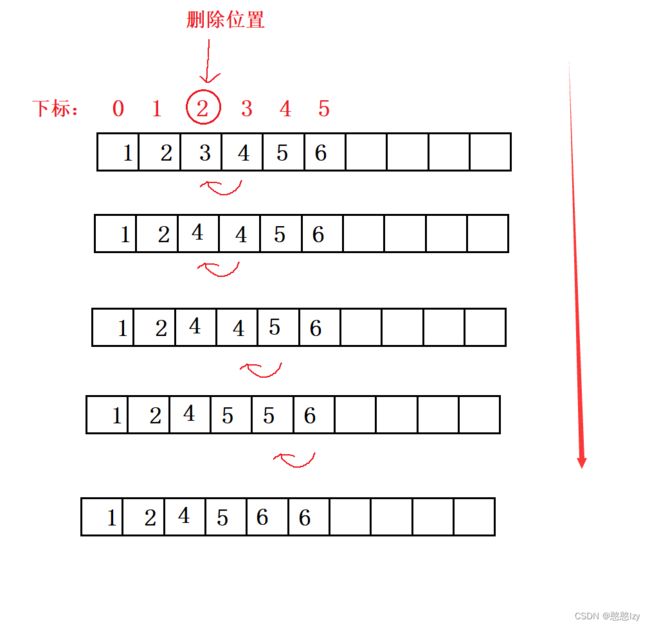
上代码：

void SeqListErse(SL* pc, int pos)//删除指定位置
{
	assert(pc);//断言
	assert(pos >= 0 && pos < pc->size);//这里断言pos>0,size>pos,间接的限制的size大于0
	for (int i = pos; i < pc->size - 1; i++)
	{
		pc->a[i] = pc->a[i + 1];
	}
	
	pc->size--;//删除后size自减1
}

查找

找到返回下标，找不到返回-1

int SeqListFind(SL* pc, SLDataType x)//查找
{
	assert(pc);//断言
	for (int i = 0; i < pc->size; i++)
	{
		if (x == pc->a[i])
		{
			return i;//找到返回下标
		}
	}
	return -1;//找不到返回-1
}