【C++】STL中 stack、queue、priority_queue的模拟实现
目录
一、 stack
1.1 stack的成员定义
1.2 实现函数功能
1.3 检验效果
1.4 适配器
1.5 代码部分
二、queue
2.1 queue的成员定义
2.2 实现函数功能
2.3 效果检验
2.4 代码部分
三、priority_queue
3.1 priority_queue的使用
3.2 仿函数
3.3 priority_queue的模拟实现
3.3.1 priority_queue 的功能
3.3.2 priority_queue的构造函数
3.3.3 插入数据/adjust_up
3.3.4 删除数据/adjust_down
3.3.5 empty判空
3.3.6 top队头数据
3.4 成果检验
3.5 代码部分
首先我们实现 stack 必定不会像之前一样从头开始模拟实现,在这里我们主要是复用STL中的现有容器来实现(vector、list、deque),本篇的重点其实是了解适配器和仿函数,掌握其使用。
比如 stack 内部我们使用 vector 来实现,因为 stack 的入栈与 vector 的尾插十分契合,vector 实现尾插、尾删的效率极其高,所以 stack 更适合使用 vector 来实现。而 queue 的插入、删除相当于是头插头删,所以我们可以使用 list 来实现。
一、 stack
1.1 stack的成员定义
我们来实现直接使用 vector 来模拟实现的 stack。
接下来我们来实现接口函数
注意,栈和队列是不支持迭代器的。如果我们想遍历,只能取一次数据,pop一次数据,直到容器为空。
1.2 实现函数功能
因为我们的函数功能都是复用的STL中的容器,代码如下,。
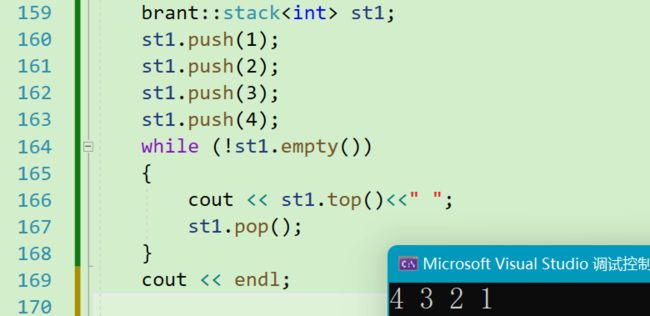
1.3 检验效果
接下来,我们使用一个案例,来检测一下实现的效果。
这样栈的功能就实现了,但是这样的栈我们还可以继续优化。比如,stack 中我们如果还是想用 list 作为容器,所以接下来我们应该如何实现呢?
1.4 适配器
这里他使用 deque 作为适配器,来解决以上的问题。
那 deque 是什么呢?deque 是一个结合了 vector、list 的容器。
头尾的插入删除非常适合,相比 vector 和 list 而言,很适合去做 stack 和queue 的默认适配容器。
想具体了解的可以去看看官方的介绍:deque的介绍
我们可以在模板中使用适配器以deque做默认值,如果使用时传入 vector 即是 vector做容器,传入list 即可让 list为容器。
那我们来看看使用适配器后,stack 中成员是如何定义的。
函数功能和调用的函数名称都是相同的。
注意点:vector 是没有 pop_front 的,在使用适配器适配 vector 时要注意一下
1.5 代码部分
namespace brant
{
template >
class stack
{
private:
Container _con;
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
T& top()
{
return _con.back();
}
bool empty()
{
return _con.empty();
}
};
} 二、queue
2.1 queue的成员定义
借鉴上面 stack 使用了适配器,并用 deque 作为默认容器,queue也可以这样定义成员变量。
2.2 实现函数功能
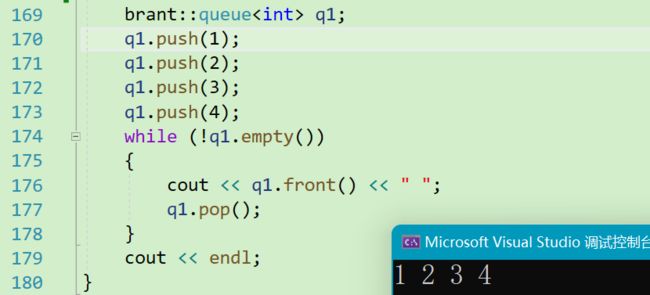
2.3 效果检验
2.4 代码部分
namespace brant
{
template >
class queue
{
private:
Container _con;
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
T& front()
{
return _con.front();
}
bool empty() const
{
return _con.empty();
}
};
} 三、priority_queue
3.1 priority_queue的使用
其底层是由堆(数据结构中的堆)实现的,其存放数据时会按堆的形式进行存放数据。默认为大堆(降序)。
其中第三个为比较的模板参数,通常传入仿函数,我们可以自己写,也可以直接使用算法库中的仿函数。需包含头文件:#include
以下是我们使用库中priority_queue的使用举例。
3.2 仿函数
仿函数又称函数对象,其实就是一个类,只不过其中重载了一个()括号运算符重载,使其非常像函数调用,所以称其为仿函数。
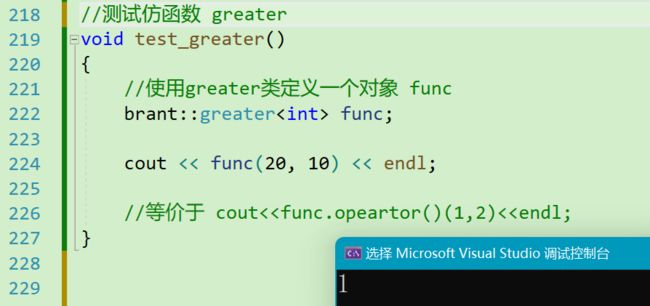
例如,如果我们实现 greater 类,就可以像下面这样定义,其实定义十分简单。
使用方式举例:
3.3 priority_queue的模拟实现
3.3.1 priority_queue 的功能
关于 priority_queue 的实现非常简单,我们其实只需要实现上面的一系列功能即可,这里一样把我们这次待实现的接口展示如下:
首先是,关于priority_queue的模板参数,第一个参数为存放的数据类型,第二个参数为适配器默认使用的容器(使用 vector、deque都可),第三个为仿函数,用来控制排序。
在我们实现 priority_queue 之前我们要明确一件事情。
Compare进行比较的仿函数 less->大堆
Compare进行比较的仿函数 greater->小堆因为 less 表示 < (小于号),例如向下调整时建立大堆时,当_con[child] < _con[parent],方能交换,如图:
所以说,less 即为大堆。greater为小堆
3.3.2 priority_queue的构造函数
关于 priority_queue 的构造函数我们主要实现2个,一个无参的构造函数,一个带参的构造函数(使用迭代器区间构造)
无参的构造函数如下:
priority_queue()
{}因为,我们使用了适配器,而适配器会默认调用库中的容器,所以我们在处理无参的构造时,可以不做任何处理,相当于就定义了一个容器。
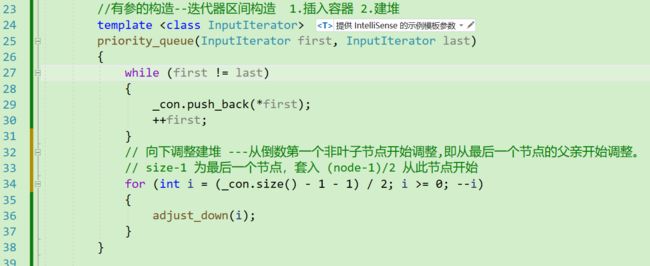
迭代器区间的构造我们要使其符合堆的特性,主要分为以下两步:
- 调用容器中的 push_back 不断尾插数据。
- 向下调整建堆(使用 adjust_down)。
代码如下(adjust_down在下面实现):
3.3.3 插入数据/adjust_up
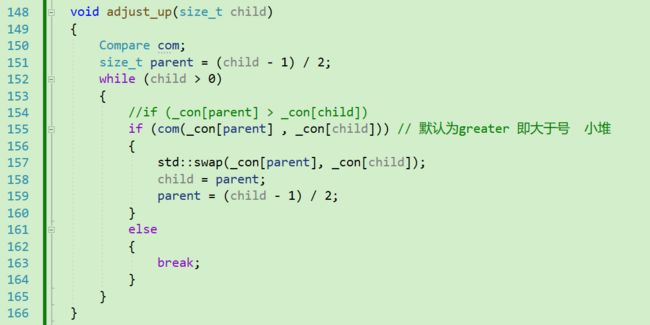
根据堆的性质,我们从尾插入数据后,为了维持堆的特性,还要对该数据进行向上调整。
因为我们之前对堆有过学习,所以写出一个向上调整也不太难。
我们如果写成上面这样,那只能实现小堆。所以,我们要调用起来模板第三个参数——仿函数,来实现比较,根据用户的传入,灵活的控制大、小堆的插入。
因为Compare 默认为 greater,即大于号,所以我们将带比较的参数传入类中,就等价于实现了大小的关系判定。
3.3.4 删除数据/adjust_down
因为我们是队列,支持的是头插头删,所以我们删除数据 pop 处理的是队头的第一个元素。
3.3.5 empty判空
3.3.6 top队头数据
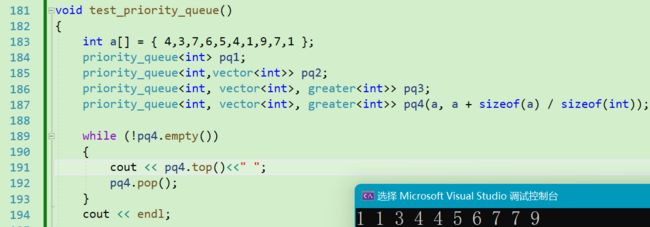
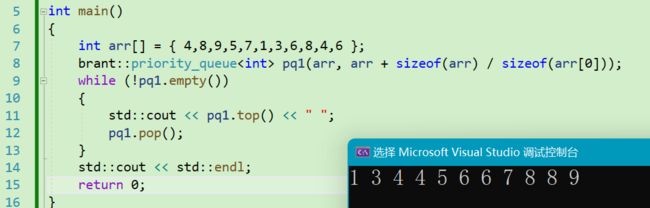
3.4 成果检验
接下来使用我们实现的priority_queue检验功能是否实现。
3.5 代码部分
namespace brant
{
//存储的数据类型 适配器 仿函数
// Compare进行比较的仿函数 less->大堆
// Compare进行比较的仿函数 greater->小堆
template ,class Compare = std::greater>
class priority_queue
{
private:
Container _con;
public:
priority_queue()
{}
//有参的构造--迭代器区间构造 1.插入容器 2.建堆
template
priority_queue(InputIterator first, InputIterator last)
{
while (first != last)
{
_con.push_back(*first);
++first;
}
// 向下调整建堆 ---从倒数第一个非叶子节点开始调整,即从最后一个节点的父亲开始调整。
// size-1 为最后一个节点,套入 (node-1)/2 从此节点开始
for (int i = (_con.size() - 1 - 1) / 2; i >= 0; --i)
{
adjust_down(i);
}
}
//插入数据然后建堆
void push(const T& x)
{
_con.push_back(x);
adjust_up(_con.size() - 1);
}
void adjust_up(size_t child)
{
Compare com;
size_t parent = (child - 1) / 2;
while (child > 0)
{
//if (_con[child] > _con[parent])
//if (_con[parent] < _con[child])
if (com(_con[parent], _con[child]))
{
std::swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void adjust_down(size_t parent)
{
Compare com;
size_t child = parent * 2 + 1;
while (child < _con.size())
{
// 选出左右孩子中大的那一个
//if (child + 1 < _con.size() && _con[child] < _con[child + 1])
if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))
{
++child;
}
//if (_con[parent] < _con[child])
if (com(_con[parent], _con[child]))
{
std::swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
const T& top()
{
return _con[0];
}
void pop()
{
std::swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
adjust_down(0);
}
bool empty()
{
return _con.empty();
}
bool empty() const
{
return _con.empty();
}
};
}