算法与数据结构(十三)：分支限界算法(0-1背包问题)（C++实现）

算法与数据结构(十三)：分支限界算法(0-1背包问题)（C++实现）

分支限界法基本思想

分支限界法常以广度优先或者最小耗费（最大效益）优先的方式搜索问题的解空间树。问题的解空间树是表示问题解空间的一颗有序树，常见的有子集树和排列树。在搜索问题的解空间树时，分支限界法和回溯法对当前扩展节点所使用的扩展方式不同。在分支限界法中，每一个活节点只有一次机会成为扩展节点。活节点一旦成为扩展节点，就一次性产生其所有儿子节点。在这些儿子节点中，那些导致不可行解或者非最优解的儿子节点被舍弃，其余儿子节点被加入活节点表中。此后，从活结点表中选取下一节点成为当前扩展节点，并重复上述节点扩展过程。这个过程一直持续到找到所求的解或活结点表为空时终止。

队列式(FIFO)分支限界法：将活节点表组织成一个队列，并按队列先进先出的原则选择下一个节点为当前扩展节点。

背包问题

背包问题分为两类，部分背包问题、背包问题。背包问题是所有装入背包的物品都必须作为一个整体，比如电器、工具等，称之为0-1背包问题。部分背包问题是指装入背包的物品可以被部分装入，比如可以切片的面包等。

对部分背包问题可以描述为给定n种物品和一个背包，n种物品的重量和价值分别为w1,w2,…,wn和v1,v2,…,vn。背包问题可以容纳的总重量为c。选择装入背包的物品，使得装入背包的物品的总价值最大。

总之，FIFO分支限界法利用一个队列来记录活节点，活节点按照FIFO原则从队列中顺序取出；初始时以根节点作为可扩展节点，此时活节点队列为空。当根节点展开时，生成两个子节点，如果这两个子节点都是可行的，则都被加入活节点队列中，根节点删除。然后再对这两个节点分别展开，如可行则加入队列中，否则删除它。一直到叶子节点，便产生了一个可行解。如果在进一步产生的可行解中都不比当前可行解好，则当前解是最优解，否则用更好的可行解替换它。当然，保留到最后的解为最优解。

主函数

/*0-1背包问题的FIFO分支限界方法*/
/*
* signed - target type will have signed representation (this is the default if omitted)
* unsigned - target type will have unsigned representation
*/
#include
#include
using namespace std;
const int MAXNUM = 10;
struct node
{
	int step;
	double price;
	double weight;
	double max;
	double min;
	unsigned int  po;
};
typedef struct node DataType;
/*顺序队列类型定义*/
struct SeQueue
{
	int f, r;
	DataType q[MAXNUM];
};
typedef struct SeQueue *pSeQueue;
pSeQueue createEmptyQueue_seq(void)
{
	pSeQueue paqu;
	paqu = (pSeQueue)malloc(sizeof(struct SeQueue));
	if (paqu == NULL)
		cout << "Out of space!!" << endl;
	else
		paqu->f = paqu->r = 0;
	return paqu;
}
int isEmptyQueue_seq(pSeQueue paqu)
{
	return paqu->f == paqu->r;
}
bool isFullQueue_seq(pSeQueue paqu)
{
	return ((paqu->r + 1) % MAXNUM) == paqu->f;
}
/*在队列中插入元素x*/
void enQueue_seq(pSeQueue paqu, DataType x)
{
	if (isFullQueue_seq(paqu))
		cout << "the Queue is Full!"<q[paqu->r] = x;
		paqu->r = (paqu->r+1) % MAXNUM;
	}
}
/*对非空队列，获取队头元素*/
DataType frontQueue_seq(pSeQueue paqu)
{
	return paqu->q[paqu->f];
}
/*删除队头元素*/
void deQueue_seq(pSeQueue paqu)
{
	if (isEmptyQueue_seq(paqu))
		cout << "Empty Queue!!";
	else
		paqu->f = (paqu->f + 1) % MAXNUM;
}
/*物品按性价比从大到小排序*/
void sort(int n, double p[],double w[])
{
	for (int i = 0; i < n - 1; i++)
		for (int j = i; j < n - 1; j++)
		{
			double a = p[j] / w[j];
			double b = p[j + 1] / w[j + 1];
			if (a < b)//换序(冒泡排序)
			{
				double temp = p[j];
				p[j] = p[j + 1];
				p[j + 1] = temp;
				temp = w[j];
				w[j] = w[j + 1];
				w[j + 1] = temp;
			}
		}
}
/*求最大可能的值*/
double up(int k, double m, int n, double p[], double w[])
{
	int i = k;
	double s = 0;
	while (i < n && w[i] < m)
	{
		m -= w[i];
		s += p[i];
		i++;
	}
	if (i < n && m>0)
	{
		s = s + m*p[i] / w[i];
		i++;
	}
	return s;
}
/*求最小可能的值*/
double down(int k, double m, int n, double p[], double w[])
{
	int i = k;
	double s = 0;
	while (i < n && w[i] < m)
	{
		m -= w[i];
		s += p[i];
		i++;
	}
	return s;
}
/*用队列实现分支限界法
* << ,>>实现二进制位移操作
* <<:左位移，>>:右位移
*1 << 1 等于 00000001 << 1 等于 00000010 等于十进制 2
*2 << 1 等于 00000010 << 1 等于 00000100 等于十进制 4
*向左移动多位。如向左移 2 位 00001110 << 2 -> 00001110
*/
double solve(double m, int n, double p[], double w[], unsigned long *po)
{
	double min;
	pSeQueue q = createEmptyQueue_seq();
	DataType x = { 0, 0, 0, 0, 0, 0 };
	sort(n, p, w);
	x.max = up(0, m, n, p, w);
	min=x.min = down(0, m, n, p, w);
	if (min == 0) return -1;
	enQueue_seq(q, x);
	while (!isEmptyQueue_seq(q))
	{
		int step;
		DataType y;
		x = frontQueue_seq(q);
		deQueue_seq(q);
		if (x.max < min) continue; //异常处理
		step = x.step + 1;
		if (step == n + 1) continue;//跳出循环
		y.max = x.price + up(step, m - x.weight, n, p, w);
		if (y.max >= min)//右子节点
		{
			y.min = x.price + down(step, m - x.weight, n, p, w);
			y.price = x.price;
			y.weight = x.weight;
			y.step = step;
			y.po = x.po << 1;
			if (y.min >= min)
			{
				min = y.min;
				if (step == n) *po = y.po;
			}
			enQueue_seq(q, y);
		}
		if (x.weight+w[step-1]<=m)//左子节点
		{
			y.max = x.price+p[step-1] + up(step, m - x.weight-w[step-1], n, p, w);
			if (y.max >= min)
			{
				y.min = x.price + p[step - 1] + down(step, m - x.weight-w[step-1], n, p, w);
				y.price = x.price + p[step - 1];
				y.weight = x.weight + w[step - 1];
				y.step = step;
				y.po = (x.po << 1)+1;
				if (y.min >= min)
				{
					min = y.min;
					if (step == n) *po = y.po;
				}
				enQueue_seq(q, y);
			}
		}

	}
	return min;
}
/*背包问题参数*/
const int n = 3;
double m = 30;
double p[n] = { 30, 20, 18 };
double w[n] = { 18, 15, 14 };
int main()
{
	double d;
	unsigned long po;
	d=solve(m, n, p, w, &po);
	if (d == -1)
		cout << "No solution!" << endl;
	else
	{
		for (int i = 0; i < n; i++)
			cout << "x" << i + 1 << "is" << ((po & (1 << (n - i - 1))) != 0) << endl;
		cout << "The max weight is:" << d << endl;
	}
	return 0;
}

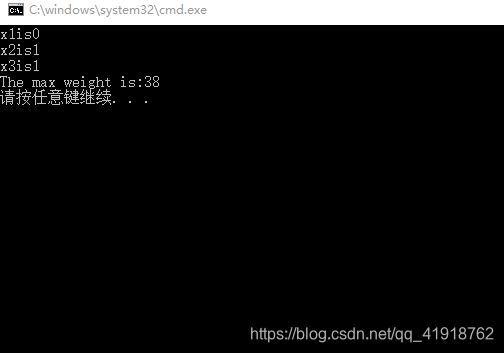
首先对队列进行定义，同时包含入队和出队操作。函数double solve(double m, int n, double p[], double w[], unsigned long *po)实现了分支限界算法。其中参数m,n.p,w分别表示背包总容量、物品数、物品的价值、物品的数量，po用来记录是否选择某个分支，用二进制0和1记录。程序运行结果如下图所示：

参考：算法分析与设计(C++描述) 石志国、刘冀伟、姚亦飞编著