SVM支持向量机对数据分类+利用SVM对股价进行预测及历史走势模拟

使用支持向量机进行数据分类，第二个代码效果不太好，需要优化。

import pandas as pd
import numpy as np
from sklearn.datasets import make_blobs
import mglearn
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
model = LinearSVC(dual=True)
from mpl_toolkits.mplot3d import Axes3D,axes3d
#找出一个超平面作为决策边界，使模型在数据上的分类误差尽量接近于小，尤其是在未知数据集上的分类误差（泛化误差）尽量小。
# 数据集引入并使用图像展示
data=pd.read_csv('SVMSet.csv',header=None)
value_counts = data.nunique()
X = pd.DataFrame();y =None

# 遍历数据框的每一列
for column in data.columns:
    unique_values = value_counts[column]
    if unique_values<=3:
        y = data[column].copy()
    else:
        X[column] = data[column].copy()
X=np.array(X);y=np.array(y)
mglearn.discrete_scatter(X,y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")


#使用SVM进行分类
linear_svm =model.fit(X,y)
mglearn.plots.plot_2d_separator(linear_svm,X)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
print(linear_svm.coef_)#array([[ 0.43604683, -0.20628571]]),解释为特征权重,数值越大表示影响越大。


#第二个特征的平方作为一个新的特征，二维变三维
X_new = np.hstack([X,X[:,1:]**2])
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
mask = y ==-1#对y每个值判别==-1？否则mask返回True（每个判别都会返回值）
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b', cmap=mglearn.cm2, s=10)#颜色为蓝色，颜色映射（color map），spot size是10
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r', marker='^', cmap=mglearn.cm2, s=10)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_zlabel("Feature 1 ** 2")


#三维
linear_svm_3d = model.fit(X_new,y)
coef,intercept = linear_svm_3d.coef_.ravel(),linear_svm_3d.intercept_
print(coef,intercept)

figure = plt.figure()
ax = Axes3D(figure,elev=-152,azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)#x_new三列数据，x轴间距划分
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX,YY = np.meshgrid(xx,yy)#创建一个坐标矩阵，其中的元素是由输入数组的所有可能组合而成的。
ZZ = (coef[0]*XX+coef[1]*YY+intercept)/-coef[2]#计算二维平面上每个网格点的高度值
#线性模型，其预测结果可以通过计算线性方程 y = coef[0]*x1 + coef[1]*x2 + coef[2]*x3 + ... + coef[n-1]*xn + intercept
ax.plot_surface(XX,YY,ZZ,rstride=8,cstride=8,alpha=0.3)
ax.scatter(X_new[mask,0],X_new[mask,1],X_new[mask,2],c='b',cmap=mglearn.cm2,s=60)
ax.scatter(X_new[~mask,0],X_new[~mask,1],X_new[~mask,2],c='r', marker='^', cmap=mglearn.cm2,s=60)
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
ax.set_zlabel("Feature 1 ** 2")


#降维
ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(),YY.ravel(),ZZ.ravel()])
plt.contourf(XX,YY,dec.reshape(XX.shape),levels=[dec.min(),0,dec.max()],cmap=mglearn.cm2,alpha=0.5)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()

 

利用SVM对股价进行预测及历史走势模拟

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
from sklearn.model_selection import cross_val_score
from sklearn import metrics
from sklearn.svm import SVR

# 辅助函数
def cross_val(model,X,Y):
    pred = cross_val_score(model, X, Y, cv=10)#预测核函数为10折交叉验证
    return pred.mean()

def print_evaluate(true, predicted):#性能评估指标（metrics）
    mae = metrics.mean_absolute_error(true, predicted)
    mse = metrics.mean_squared_error(true, predicted)#均方误差
    rmse = np.sqrt(metrics.mean_squared_error(true, predicted))
    r2_square = metrics.r2_score(true, predicted)
    print('MAE:', mae)
    print('MSE:', mse)
    print('RMSE:', rmse)
    print('R2 Square', r2_square)
    print('__________________________________')

# 加载数据集
data=pd.read_csv('cn600169.csv')
features=pd.DataFrame();target=None
features['成交量']= data['成交量（手）'];features['成交量']=features['成交量'].astype(float)
features['换手率']=data['换手率'];features['换手率']=features['换手率'].str.rstrip('%').astype(float)
target=data['收盘'];target=target.astype(float)

#数据归一化处理
min_max_scaler = preprocessing.MinMaxScaler()#X_scaled = (X - X_min) / (X_max - X_min)
features = min_max_scaler.fit_transform(features)#两列数据转化

#数据集划分
split_num=int(len(features)*0.96)
X_train=features[:split_num]
Y_train=target[:split_num]
X_test=features[split_num:]
Y_test=target[split_num:]

#支持向量机建模，在输入空间中计算两个样本点之间的相似性，即样本点附近的样本对目标分类的贡献大，远离的样本对分类的影响较小。
svm_reg = SVR(kernel='rbf', C=30, epsilon=0.01)#计算样本点之间的高斯分布相似度来进行非线性映射。RBF核函数的表达式为：K(x, y) = exp(-gamma * ||x - y||^2)
print(cross_val(svm_reg,X_train, Y_train))
svm_reg.fit(X_train, Y_train)#模型拟合，用训练集，训练好后进行预测
test_pred = svm_reg.predict(X_test)
train_pred = svm_reg.predict(X_train)
print('Test set evaluation:\n_____________________________________')
print_evaluate(Y_test, test_pred)
print('Train set evaluation:\n_____________________________________')
print_evaluate(Y_train, train_pred)

# 可视化部分
sns.set(font_scale=1.2)
plt.rcParams['font.sans-serif']='SimHei'
plt.rcParams['axes.unicode_minus']=False
plt.rc('font',size=14)
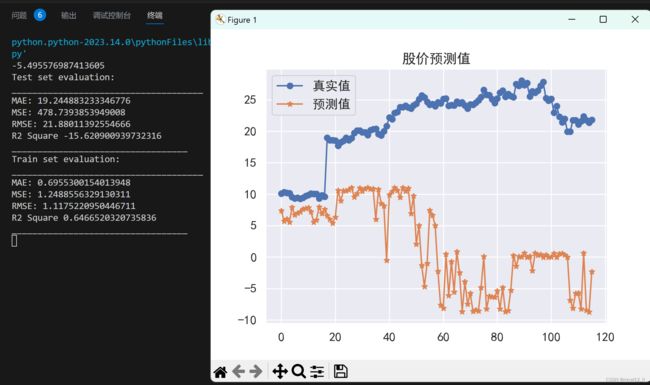
plt.plot(list(range(0,len(X_test))),Y_test,marker='o')
plt.plot(list(range(0,len(X_test))),test_pred,marker='*')
plt.legend(['真实值','预测值'])
plt.title('股价预测值')
plt.show()