常见排序算法性能分析比较(快排,希尔,堆排,归并,插入排序等)
文章目录
- 1.各种排序算法实现及其特点
-
- 1.1 直接插入排序
- 1.2 希尔排序
- 1.3 直接选择排序
- 1.4 堆排序
- 1.5 冒泡排序
- 1.6 快速排序
- 1.7 归并排序
- 1.8 计数排序
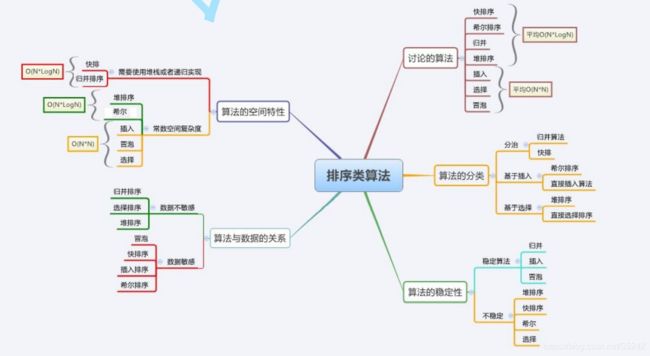
- 2.排序算法复杂度及稳定性分析
1.各种排序算法实现及其特点
1.1 直接插入排序
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//直接插入排序-从前往后比较
void InsertSort_1(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
int k = left;
while (ar[i] > ar[k])
k++;
int tmp = ar[i];
for (int j = i; j > k; --j)
ar[j] = ar[j - 1];
ar[k] = tmp;
}
}
//直接插入排序-从后往前比较
void InsertSort_2(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
int j = i;
while (j > left && ar[j] < ar[j - 1])
{
Swap(&ar[j], &ar[j - 1]);
j--;
}
}
}
//直接插入排序-从后往前比较不调用交换函数
void InsertSort_3(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
int j = i;
int tmp = ar[j];
while (j > left && tmp < ar[j - 1])
{
ar[j] = ar[j - 1];
j--;
}
ar[j] = tmp;
}
}
//直接插入排序-哨兵位
void InsertSort_4(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
ar[0] = ar[i]; //哨兵位
int j = i;
while (ar[0] < ar[j - 1])
{
ar[j] = ar[j - 1];
j--;
}
ar[j] = ar[0];
}
}
//折半插入排序
void BinInsertSort(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
int tmp = ar[i];
int low = left;
int high = i - 1;
int mid;
while (low <= high) //折半查找插入位置
{
mid = (low + high) / 2;
if (tmp >= ar[mid])
low = mid + 1;
if (tmp < ar[mid])
high = mid - 1;
}
for (int j = i; j > low; --j)
ar[j] = ar[j - 1];
ar[low] = tmp;
}
}
//二路插入排序 空间复杂度 O(n)
void TwoWayInsertSort(int* ar, int left, int right)
{
int n = right - left;
int* tmp = (int*)malloc(sizeof(int) * n);
tmp[0] = ar[left];
int first, final;
first = final = 0;
for (int i = left + 1; i < right; ++i)
{
if (ar[i] < tmp[first])
{
first = (first - 1 + n) % n;
tmp[first] = ar[i];
}
else if (ar[i] >= tmp[final])
{
tmp[++final] = ar[i];
}
else
{
int end = final;
while (ar[i] < tmp[end])
{
tmp[(end + 1) % n] = tmp[end];
end = (end - 1 + n) % n;
}
tmp[(end + 1) % n] = ar[i];
final++;
}
}
int k = 0;
for (int i = first; k < n; ++k)
{
ar[k] = tmp[i];
i = (i + 1) % n;
}
free(tmp);
}
1.2 希尔排序
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 - 希尔排序的时间复杂度不好计算,需要进行推导,推导出来平均时间复杂度: O(N1.3—N2)
- 稳定性:不稳定。
void ShellSort(int* ar, int left, int right)
{
int gap = right - left;
while (gap > 1)
{
gap = gap / 3 + 1; //4 2 1 设计文档
for (int i = left + gap; i < right; ++i)
{
if (ar[i] < ar[i - gap])
{
int tmp = ar[i];
int j = i;
while (j > left && tmp < ar[j - gap])
{
ar[j] = ar[j - gap];
j = j - gap;
}
ar[j] = tmp;
}
}
}
}
1.3 直接选择排序
直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//简单选择排序
int GetMinIndex(int* ar, int left, int right)
{
int min_value = ar[left];
int index = left;
for (int i = left + 1; i < right; ++i)
{
if (ar[i] < min_value)
{
min_value = ar[i];
index = i;
}
}
return index;
}
void SelectSort(int* ar, int left, int right)
{
for (int i = left; i < right - 1; ++i)
{
int index = GetMinIndex(ar, i, right);
if (index != i)
Swap(&ar[i], &ar[index]);
}
}
1.4 堆排序
堆排序:需要注意的是排升序要建大堆,排降序建小堆。
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
//堆排 这里是升序排列 建立大堆 需要向下调整
void _AdjustDown(int* ar, int left, int right, int start)
{
int n = right - left;
int i = start; //代表父节点
int j = 2 * i + 1; //代表i节点的左子树
int tmp = ar[i];
while (j < n)
{
if (j + 1 < n && ar[j] < ar[j + 1])
j = j + 1;
if (tmp < ar[j])
{
ar[i] = ar[j];
i = j;
j = 2 * i + 1;
}
else
break;
}
ar[i] = tmp;
}
void HeapSort(int* ar, int left, int right)
{
int n = right - left;
int curpos = n / 2 - 1 + left; //找到二叉树的最后一个分支
while (curpos >= 0)
{
_AdjustDown(ar, left, right, curpos);
curpos--;
}
//排序
int end = right - 1;
while (end > left)
{
Swap(&ar[left], &ar[end]); //出堆
_AdjustDown(ar, left, end, 0);
end--;
}
}
1.5 冒泡排序
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
//冒泡排序
void BubbleSort_1(int* ar, int left, int right)
{
for (int i = left; i < right - 1; ++i)
{
for (int j = left; j < right - i - 1; ++j)
{
if (ar[j] > ar[j + 1])
{
Swap(&ar[j], &ar[j + 1]);
}
}
}
}
//改进 无交换时可以退出循环
void BubbleSort_2(int* ar, int left, int right)
{
bool is_swap = false;
for (int i = left; i < right - 1; ++i)
{
for (int j = left; j < right - i - 1; ++j)
{
if (ar[j] > ar[j + 1])
{
Swap(&ar[j], &ar[j + 1]);
is_swap = true;
}
}
if (!is_swap)
break;
else
is_swap = false;
}
}
1.6 快速排序
快速排序:
实现方法常有三种:
1. hoare版本
2. 挖坑法
3. 前后指针版本
代码实现均有。
特点:
1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(logN)
4. 稳定性:不稳定
//快速排序
int GetMidIndex(int* ar, int left, int right)
{
int mid = (left + right - 1) / 2;
if (ar[left] < ar[mid] && ar[mid] < ar[right - 1])
return mid;
if (ar[left] > ar[mid] && ar[left] < ar[right - 1])
return left;
return right - 1;
}
//hoare 法
int _Partition_1(int* ar, int left, int right)
{
int low = left, high = right - 1;
int key = ar[low];
while (low < high)
{
while (low<high && ar[high]>key)
high--;
Swap(&ar[low], &ar[high]);
while (low < high && ar[low] <= key)
low++;
Swap(&ar[low], &ar[high]);
}
return low;
}
//挖坑法
int _Partition_2(int* ar, int left, int right)
{
int low = left, high = right - 1;
int key = ar[low];
while (low < high)
{
while (low<high && ar[high]>key)
high--;
ar[low] = ar[high];
while (low < high && ar[low] <= key)
low++;
ar[high] = ar[low];
}
ar[low] = key;
return low; //曲轴点
}
//前后指针法
int _Partition_3(int* ar, int left, int right)
{
int mid_index = GetMidIndex(ar, left, right); //前中后三者取中间值作为用来比较的值
if (mid_index != left)
Swap(&ar[mid_index], &ar[left]);
///
int key = ar[left];
int pos = left;
for (int i = pos + 1; i < right; ++i)
{
if (ar[i] < key)
{
pos++;
if (pos != i)
{
Swap(&ar[pos], &ar[i]);
}
}
}
Swap(&ar[left], &ar[pos]);
return pos;
}
#define M 5
void QuickSort(int* ar, int left, int right)
{
if (left >= right)
return;
if (right - left <= M) //改进 这里元素个数少的时候 选择插入排序
InsertSort_3(ar, left, right);
else
{
int pos = _Partition_3(ar, left, right);
QuickSort(ar, left, pos); // 左子序列
QuickSort(ar, pos + 1, right); // 右子序列
}
}
1.7 归并排序
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
//归并排序
void _MergeSort(int* ar, int left, int right, int* tmp)
{
if (left >= right)
return;
int mid = (left + right) / 2;
_MergeSort(ar, left, mid, tmp); // 分解左边分支
_MergeSort(ar, mid + 1, right, tmp); //分解右边分支
//开始归并
int begin1, end1, begin2, end2;
begin1 = left, end1 = mid;
begin2 = mid + 1, end2 = right;
int k = left; //
while (begin1 <= end1 && begin2 <= end2)
{
if (ar[begin1] < ar[begin2])
tmp[k++] = ar[begin1++];
else
tmp[k++] = ar[begin2++];
}
while (begin1 <= end1)
tmp[k++] = ar[begin1++];
while (begin2 <= end2)
tmp[k++] = ar[begin2++];
memcpy(ar + left, tmp + left, sizeof(int) * (right - left + 1));
}
void MergeSort(int* ar, int left, int right)
{
int n = right - left;
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(ar, left, right - 1, tmp);
free(tmp);
}
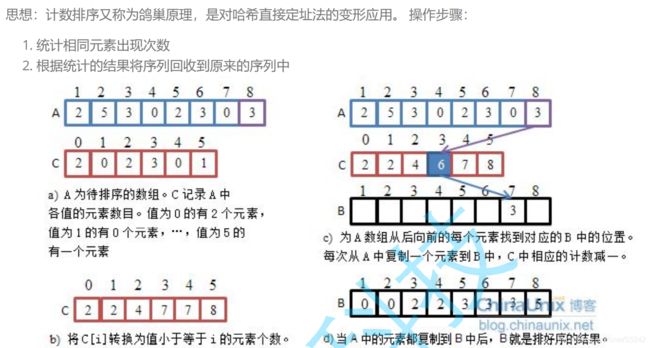
1.8 计数排序
计数排序为非比较排序:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限.
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
- 稳定性:稳定