判别式模型和生成式模型
在机器学习中,对于有监督学习可以将其分为两类模型:判别式模型和生成式模型。简单地说,判别式模型是针对条件分布建模,而生成式模型则针对联合分布进行建模。
01 基本概念
假设我们有训练数据(X,Y),X是属性集合,Y是类别标记。这时来了一个新的样本样本 x ,我们想要预测它的类别y。
我们最终的目的是求得最大的条件概率 P(y|x)作为新样本的分类。
- 判别式模型这么做
根据训练数据得到分类函数和分界面,比如说根据SVM模型得到一个分界面,然后直接计算条件概率 P(y|x),我们将最大的 P(y|x)。
作为新样本的分类。判别式模型是对条件概率建模,学习不同类别之间的最优边界,无法反映训练数据本身的特性,能力有限,其只能告诉我们分类的类别。
- 生成式模型这么做
一般会对每一个类建立一个模型,有多少个类别,就建立多少个模型。比如说类别标签有{猫,狗,猪},那首先根据猫的特征学习出一个猫的模型,再根据狗的特征学习出狗的模型,之后分别计算新样本X跟三个类别的联合概率 P(y|x),然后根据贝叶斯公式:
分别计算 P(y|x),选择三类中最大的 P(y|x)作为样本的分类。
3.两个模型的小结
不管是生成式模型还是判别式模型,它们最终的判断依据都是条件概率 P(y|x),但是生成式模型先计算了联合概率P(x,y),再由贝叶斯公式计算得到条件概率。因此,生成式模型可以体现更多数据本身的分布信息,其普适性更广。
02 用例子说明概念
- 山羊绵羊的例子
判别式模型:要确定一个羊是山羊还是绵羊,用判别式模型的方法是从历史数据中学习到模型,然后通过提取这只羊的特征来预测出这只羊是山羊的概率,是绵羊的概率。
生成式模型:是根据山羊的特征首先学习出一个山羊的模型,然后根据绵羊的特征学习出一个绵羊的模型,然后从这只羊中提取特征,放到山羊模型中看概率是多少,再放到绵羊模型中看概率是多少,哪个大就是哪个。
- 模型范例
假设现在有一个分类问题,X是特征,Y是类标记。用判别式模型学习一个条件概率分布 P(y|x),用生成式模型学习一个联合概率分布P(x,y)。
用一个简单的例子来说明这个问题。假设X就是两个特征(1或2),Y有两类(0或1),有如下训练样本(1,0)、(1,0)、(1,1)、(2,1)。
则学习到的条件概率分布(判别式模型)如下:
而学习到的联合概率分布(生成式模型)如下:
在实际分类问题中,判别式模型可以直接用来判断特征的类别情况;而生成式模型需要加上贝叶斯公式,然后应用到分类中。但是,生成式模型的概率分布可以有其他应用,就是说生成式模型更一般更普适。不过判别式模型更直接,更简单。两种方法目前交叉较多。由生成式模型可以得到判别式模型,但由判别式模型得不到生成式模型。
03 判别式模型和生成式模型的区别
-
判别式模型和生成式模型的对比图
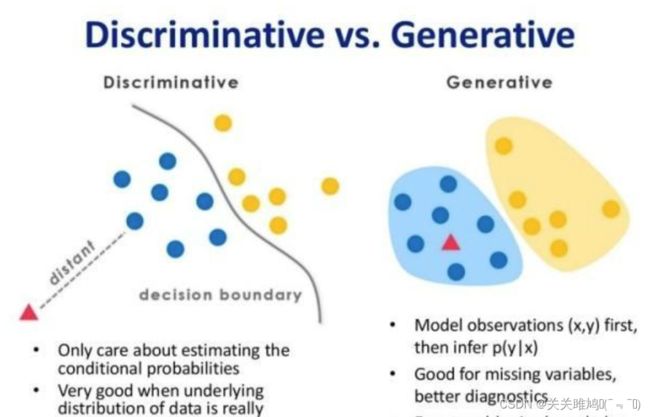
上图左边为判别式模型而右边为生成式模型,可以很清晰地看到差别,判别式模型是在寻找一个决策边界,通过该边界来将样本划分到对应类别。而生成式模型则不同,它学习了每个类别的边界,它包含了更多信息,可以用来生成样本。 -
判别式模型和生成式模型的特点
判别式模型特点:
判别式模型直接学习决策函数Y=f(X),或者条件概率P(Y|X),不能反映训练数据本身的特性,但它寻找不同类别之间的最优分裂面,反映的是异类数据之间的差异,直接面对预测往往学习准确度更高。具体来说有以下特点:
对条件概率建模,学习不同类别之间的最优边界。
捕捉不同类别特征的差异信息,不学习本身分布信息,无法反应数据本身特性。
学习成本较低,需要的计算资源较少。
需要的样本数可以较少,少样本也能很好学习。
预测时拥有较好性能。
无法转换成生成式。
生成式模型的特点:
生成式模型学习的是联合概率密度分布P(X,Y),可以从统计的角度表示分布的情况,能够反映同类数据本身的相似度,它不关心到底划分不同类的边界在哪里。生成式模型的学习收敛速度更快,当样本容量增加时,学习到的模型可以更快的收敛到真实模型,当存在隐变量时,依旧可以用生成式模型,此时判别式方法就不行了。具体来说,有以下特点:
对联合概率建模,学习所有分类数据的分布。
学习到的数据本身信息更多,能反应数据本身特性。
学习成本较高,需要更多的计算资源。
需要的样本数更多,样本较少时学习效果较差。
推断时性能较差。
一定条件下能转换成判别式。
总之,判别式模型和生成式模型都是使后验概率最大化,判别式是直接对后验概率建模,而生成式模型通过贝叶斯定理这一“桥梁”使问题转化为求联合概率。
