【笔记】Hawkes Process:超详细带示例的讲解
最近准备学Hawkes Process, 但是找遍了百度,b站,谷歌和youtube,都没有找到通俗易懂的讲解。今天终于在拆老师(ChatGPT)的帮助下搞懂了!关于使用ChatGPT进行自学的Prompt可以看之前的笔记:【笔记】 如何使用ChatGPT得到更满意的结果:Prompt Engineering (1)_Dorothy30的博客-CSDN博客
这一篇笔记仅是针对于Hawkes Process的基础知识介绍,可能并不全面,但应该可以理解的比较好!(感谢ChatGPT老师!)
Hawkes Process是一种在各个领域都有应用的对事件进行统计建模方法,是一种自我激励的点过程(point process),可以帮助我们了解事件是如何随时间发生的。
目录
Hawkes Process的数学表达式
在社交网络的场景下进一步理解Hawkes Process数学表达式
使用Python对一维的Hawkes process进行模拟
在正式介绍Hawkes Process之前,我们先通过一个例子来了解它表述的过程大概是什么样的。
想象一下你正在参加一个聚会,人们开始鼓掌。 当一个人开始鼓掌时,可能会让其他人也想开始鼓掌,然后带动了更多人鼓掌,依此类推。 这个鼓掌的带动作用就类似于Hawkes Process的工作原理。
Hawkes Process就像一场“popcorn”游戏,一个的历史事件的发生会导致另一个后续事件的发生,这个后续事件的发生又会对下一个事件的发生产生影响,就像连锁反应!但这种一级接一级的影响最终会停止,就像在聚会上每个人都厌倦了鼓掌,或者派对结束了一样,这被称为Hawkes Process的“end time”。
Hawkes Process的数学表达式
正如之前提到的一样,Hawkes Process是一种点过程,是一种对随机发生的事件进行建模的方法。 在Hawkes Process,事件可以触发其他事件,从而产生活动的“级联”或“多米诺骨牌效应”。
Hawkes Process的基本数学表达式是由 λ(t), μ和 α三个参数决定的:
![]()
- λ(t) :Hawkes Process在时间 t 的“intensity”或“rate”。 换句话说,它是给定到该点之前发生的所有过去事件的情况下,在时间 t 附近的一个小时间间隔$\triangle t$内发生的事件的期望值。
- μ:Hawkes Process的“background rate”。 这是在没有任何触发或级联效应的情况下事件发生的rate。意思是说,在不受任何其他事情的影响下,一件事情的发生本身就具有一定的概率,这个基础的概率用μ表示。
- α :是一个“triggering kernel”(也就是触发事件发生的核函数),它描述了过去的事件如何影响未来的事件。 它是一个取决于每个过去事件发生的时间的函数,衡量每个过去事件对当前给定的任意时间的影响强度(对当前事件发生intensity的影响)。
- 核函数有很多种表达方式,这取决于具体的应用场景,但也有一些常用的函数表达。
在社交网络的场景下进一步理解Hawkes Process数学表达式
现在让我们考虑一个在社交网络下的场景,在这个社交网络中,用户可以在其中发布消息,每条消息都可以触发其他用户发布消息。 我们可以将这个sending posts的出发现象建模为Hawkes Process,其中每条消息都是一个事件,触发效果( triggering effect)由triggering kernel(核函数)进行表示。
例如,我们可以把这个场景下给定时间的intensity表示为:
![]()
在这里,
- μ 表示消息发布的background rate(即,如果没有触发效果,消息发布自身就具有的频率)
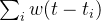 代表了过去事件的影响,通过索引 i 遍历时间 t 之前发生的所有过去的消息 t_i
代表了过去事件的影响,通过索引 i 遍历时间 t 之前发生的所有过去的消息 t_i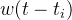 是triggering kernel,表示每个过去的消息对时间 t intensity的权重或影响。(请注意,在社交网络示例中,的确可以将triggering kernel写为
是triggering kernel,表示每个过去的消息对时间 t intensity的权重或影响。(请注意,在社交网络示例中,的确可以将triggering kernel写为 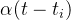 而不是
而不是 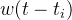 。 但在这里使用
。 但在这里使用 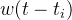 的原因是因为它是每个过去事件的“权重”或“影响”的另一个通用表达,也就是说可以用不同的字母或者方程来描述triggering kernel)
的原因是因为它是每个过去事件的“权重”或“影响”的另一个通用表达,也就是说可以用不同的字母或者方程来描述triggering kernel)
在这个场景下,triggering kernel ![]() 可以表示为:
可以表示为:
![]()
- α 是triggering effect的强度大小(即,每条过去的消息会增加未来消息的intensity)
- β 是一个“decay rate”,它决定了过去消息的影响随时间衰减的速度(也就是说过去事件对未来事件的影响不是固定的,而是会随着时间减弱的)。
看到这里,你可能还会疑惑,这个intensity到底是什么意思,过去发生的事件到底如何影响着未来的事件。如果你也有这样和我最开始一样的疑惑的话,就继续看下去吧!
使用Python对一维的Hawkes process进行模拟
使用Python对一维的Hawkes process进行模拟的代码如下:
import numpy as np
import matplotlib.pyplot as plt
from tick.hawkes import SimuHawkesExpKernels
# Set up simulation parameters
n_nodes = 1
end_time = 100
mu = 0.1 # background rate
alpha = 0.8 # triggering kernel amplitude
beta = 2 # triggering kernel decay rate
# Create simulation object
simu = SimuHawkesExpKernels(
adjacency=np.array([[alpha]]), # adjacency matrix with only one node
decays=beta, # decay rate for the kernel
baseline=np.array([mu]), # background rate
end_time=end_time,
verbose=False,
seed=10
)
# Simulate the process
simu.simulate()
# Extract the event times and estimate the kernel function
times = simu.timestamps[0] # an array of event times (timestamps)
t_grid = np.linspace(0, end_time, num=1000)
kernel = alpha * np.exp(-beta * t_grid)
# Compute the intensity function and plot it
intensity = np.zeros_like(t_grid)
for i, t in enumerate(t_grid):
idx = np.where(times < t)[0]
# np.where(times < t) returns a tuple containing the indices of all the elements in
# the numpy array times that satisfy the condition times < t
if len(idx) > 0:
# For example, suppose t_grid is [0.0, 0.1, 0.2, 0.3, ..., 99.8, 99.9, 100.0] and times[idx] is
# [5.6, 12.3, 35.2, 98.7]. The np.searchsorted function would return [56, 123, 352, 987], which are the indices
# in t_grid that correspond to the event times in times[idx].
intensity[i] = mu + np.sum(kernel[i - np.searchsorted(t_grid, times[idx])])
else:
intensity[i] = mu
plt.plot(t_grid, intensity)
plt.xlabel('Time')
plt.ylabel('Intensity')
plt.title(f'Hawkes process with mu={mu}, alpha={alpha}, beta={beta}')
plt.show()在这个代码中,我们使用了tick这个package来进行Hawkes process的模拟,其中,我们使用SimuHawkesExpKernels 函数来模拟具有指数kernel的Hawkes process。代码中设定的参数如下:
- mu:background rate,表示在没有任何触发事件的情况下用户发消息率
- alpha:过去事件trigger未来事件的幅度,也就是触发效应的强弱
- beta:decay rate,表示过去帖子的触发效果随时间衰减的速度
- end_time:模拟的时间范围
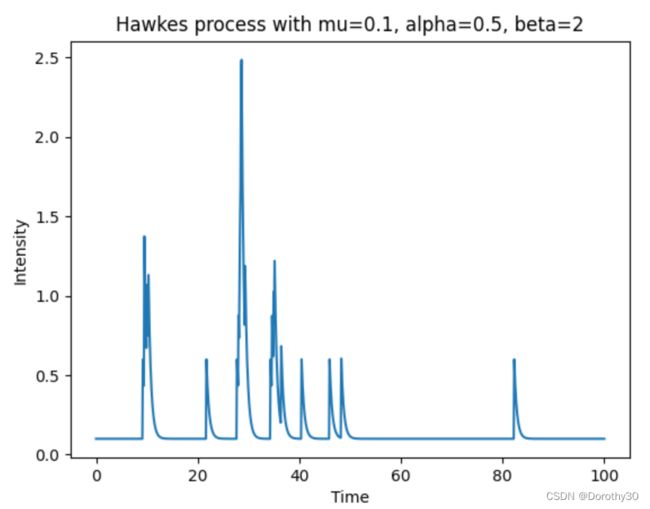
例如,假设我们设置 mu = 0.1,alpha = 0.5,beta = 2.0,模拟100分钟的过程。然后SimuHawkesExpKernels 函数将生成用户发帖的随机timestamp(时间戳)。 生成的时间戳数将取决于我们为函数设置的参数mu,和triggering kernel的alpha 和 beta等。例如,这个函数会返回,用户将会在[9, 21, 28, 35]的timestamp上发帖。上述代码计算的intensity曲线如下图所示:
结合我们的社交网络背景来进行图的解释的话,我们可以假设现在有一个社交媒体用户,他过去在[9, 21, 28, 35]的时间戳上发布了 4 次帖子。我们想使用 Hawkes 过程来基于他们过去的发帖行为,预测该用户在40分钟的时候会发多少帖子。
现在,我们要计算该用户在每个timestamp的intensity function。 intensity function告诉我们,根据用户过去的行为,用户在特定时间发帖的可能性有多大。假设我们要计算时间 40 的intensity 。我们计算用户在40分钟之前发布的过去帖子的数量,即 4。然后我们使用triggering kernel计算每个过去的帖子对第40分钟的instensity的贡献,即使用![]() ,其中 t 是当前时间,
,其中 t 是当前时间,![]() 是过去发布的时间戳。
是过去发布的时间戳。
例如,第一个过去的帖子(时间戳 9)对第40分钟的intensity的贡献是:0.5 * exp(-2.0 * (40 - 9)) = 5.9 e-28。 我们对过去的每个帖子都这样做,并总结贡献以获得第40分钟的总intensity,为2.27 e-05 + 0.1 = 0.1。这意味着根据用户过去的行为,我们预测他们可能会在接下来的第40分钟内会发 0.1次左右的帖子。 但是,这只是基于模型的预测,用户发布的实际帖子数量可能因各种因素而有所不同。(注意,这里计算的结果与图片不吻合的原因是,图片里模拟了100次发帖的事件, 在40分钟前的timestamp数量并不是4次,而是更多)
所以,请务必注意,intensit计算并不能直接被解释为用户将在下一个时间戳发布的帖子数。 它只是根据用户过去的发帖行为,估算用户在任何给定时间可能发帖的瞬时速率,例如在40分钟里发帖的瞬时速度为0.1贴/ 分钟。实际的瞬时速度肯定是在更小的时间区间下来说的,这里只是举例说明。
以上就是关于Hawkess process的基础数学表达式的讲解以及结合实际场景的说明。需要最后额外补充的是,Hawkess process的应用场景还有很多,例如地震、金融、机器学习、可靠性、神经科学、信息传播、保险、专利和论文引用、心理学、疾病预测、物种入侵等等。以地震为例,每一次地震都可能会导致附近发生其他地震。 通过研究地震的Hawkes Process,科学家们可以尝试预测下一次地震可能发生的时间和地点。当然这里指的Hawkes Process是基于基础表达式而设计的更为复杂的Hawkes Process表达。
我之后还会继续深入学习Hawkes Process,下一步应该是学习多维的Hawkes Process模拟和表达,希望不要学的太痛苦。最后,感谢ChatGPT老师的详解和帮助!!