【算法修炼】图论算法三(并查集的应用、图中的环、Kruskal最小生成树算法、Dijkstra最短路径算法、SPFA最短路径算法)
图论算法三
-
-
- 一、并查集算法的应用
-
- 图中的环(中等)用并查集找图的环数
- 等式方程的可满足性(中等)
- 二、Kruskal最小生成树
-
- Kruskal 算法
- 最低成本联通所有城市(中等)
- 二维数组的排序(选择第几个元素为排序依据)
- 连接所有点的最小费用(中等)
- 1142 繁忙的都市(简单)
- 1143 联络员
- 1144 连接格点
- 三、Dijkstra 算法框架
-
- 无权图和有权图中的BFS区别
- 网络延迟时间(中等)
- ※四、SPFA算法框架、负环判断方法
-
一、并查集算法的应用
再来回顾下并查集算法的模板:
class UF {
// 连通分量个数
int count;
// 存储若干棵树
int[] parent;
// 记录每棵树的重量
int[] size;
// 构造函数
public UF(int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
// 图中的每个节点指向自己
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 找 x节点的根节点
public int find(int x) {
// 用路径压缩
while (parent[x] != x) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
// 连通p、q节点
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
// 根节点相同,说明本来就是连通的
if (rootP == rootQ) {
return;
}
// 小树接在大树下,更平衡
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
// 连通分量个数--
count--;
}
// 判断 p 和 q 是否连通
public boolean connected(int p, int q) {
return find(p) == find(q);
}
// 返回连通分量个数
public int count() {
return count;
}
}
算法的关键点有 3 个:
1、用 parent 数组记录每个节点的父节点,相当于指向父节点的指针,所以 parent 数组内实际存储着一个森林(若干棵多叉树)。
2、用 size 数组记录着每棵树的重量,目的是让 union 后树依然拥有平衡性,而不会退化成链表,影响操作效率。
3、在 find 函数中进行路径压缩,保证任意树的高度保持在常数,使得 union 和 connected API 时间复杂度为 O(1)。
别忘了路径压缩,小树接在大树后面,更平衡。
图中的环(中等)用并查集找图的环数
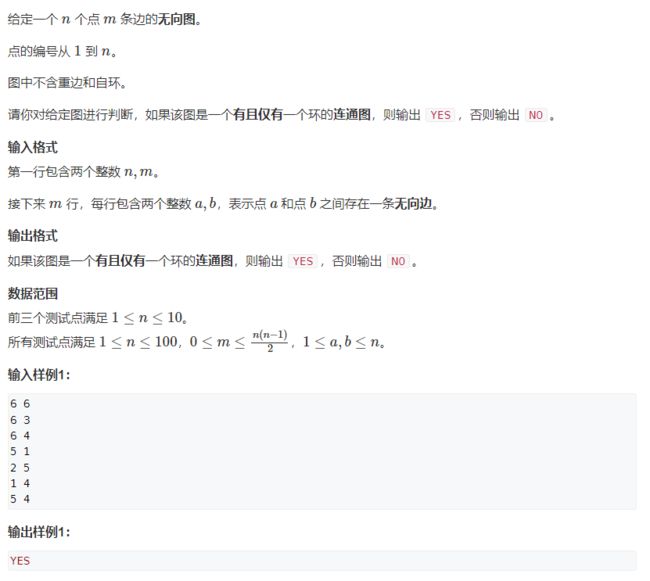
有且仅有一个环的,连通图,连通可以用并查集,环的个数的检测其实也可以用并查集!所以把并查集模板背熟就好。
import java.util.*;
import java.io.*;
public class Main {
static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
String[] input = reader.readLine().trim().split(" ");
int n = Integer.parseInt(input[0]);
int m = Integer.parseInt(input[1]);
List<int[]> graph = new LinkedList<>(); // 1-n
while (m-- > 0) {
input = reader.readLine().trim().split(" ");
int u = Integer.parseInt(input[0]);
int v = Integer.parseInt(input[1]);
// 无向图双向边
graph.add(new int[] {u, v});
}
// 并查集
UF uf = new UF(n + 1); // 1-n
int circle = 0;
for (int[] cur : graph) {
// 图中两个点已经连通说明产生一个环
if (uf.connected(cur[0], cur[1])) {
// 成环了
circle++;
continue;
}
uf.union(cur[0], cur[1]);
}
if (uf.count() == 2 && circle == 1) {
// 连通且环数=1
writer.write("YES" + "\n");
} else {
writer.write("NO" + "\n");
}
writer.flush();
}
}
class UF {
int count;
int[] parent;
int[] size;
UF (int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
int find(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
boolean connected(int p, int q) {
return find(p) == find(q);
}
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
if (size[rootP] > size[rootQ]) {
// 小树接在大树下面
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
// 连通分量--
count--;
}
int count() {
return count;
}
}
等式方程的可满足性(中等)
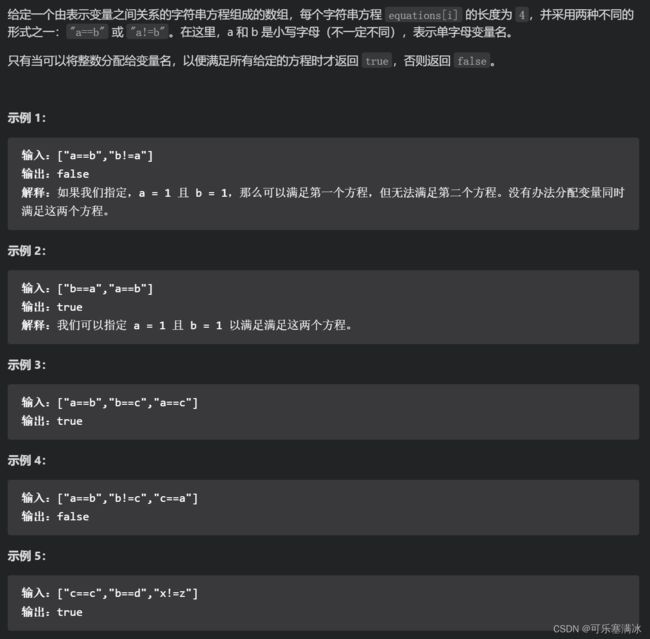
前文说过,动态连通性其实就是一种等价关系,具有「自反性」「传递性」和「对称性」,其实 == 关系也是一种等价关系,具有这些性质。所以这个问题用 Union-Find 算法就很自然。
核心思想是,将 equations 中的算式根据 == 和 != 分成两部分,先处理 == 算式,使得他们通过相等关系各自勾结成门派(连通分量);然后处理 != 算式,检查不等关系是否破坏了相等关系的连通性。
class Solution {
public boolean equationsPossible(String[] equations) {
// 26个英文字母
UF uf = new UF(26);
// 先让相等的字母形成连通分量 ==
for (String eq : equations) {
if (eq.charAt(1) == '=') {
char x = eq.charAt(0);
char y = eq.charAt(3);
uf.union(x - 'a', y - 'a');
}
}
// check不等关系是否会打破相等关系的连通性
// 如果没有打破,说明这个不等关系是不会影响其它等式的判断
// a != b,打破就是说 a 与 b 原来是连通的,现在不等式又连通了,那肯定false
for (String eq : equations) {
if (eq.charAt(1) == '!') {
char x = eq.charAt(0);
char y = eq.charAt(3);
// 如果相等关系成立(也就是之前已经连通了),则逻辑冲突
if (uf.connected(x - 'a', y - 'a')) return false;
}
}
return true;
}
}
class UF {
// 连通分量个数
int count;
// 每棵树
int[] parent;
// 每棵树的节点数
int[] size;
UF(int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
// 图中的每个节点指向自己
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 找根节点
public int find(int x) {
while (parent[x] != x) {
// 路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
// 判断是否连通
public boolean connected(int p, int q) {
return find(p) == find(q);
}
// 连通两个节点
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
// 本来就联通
if (rootQ == rootP) return;
if (size[rootP] > size[rootQ]) {
// 小树接在大树后
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
// 连通分量--
count--;
}
// 返回连通分量个数
public int count() {
return count;
}
}
一定要学会把问题转换为并查集的思路,这样能够帮助解决很多问题。
二、Kruskal最小生成树
如果一幅图没有环,完全可以拉伸成一棵树的模样。说的专业一点,树就是「无环连通图」。
那么什么是图的「生成树」呢,其实按字面意思也好理解,就是在图中找一棵包含图中的所有节点的树。专业点说,生成树是含有图中所有顶点的「无环连通子图」。
容易想到,一幅图可以有很多不同的生成树,比如下面这幅图,红色的边就组成了两棵不同的生成树

对于加权图,每条边都有权重,所以每棵生成树都有一个权重和。比如上图,右侧生成树的权重和显然比左侧生成树的权重和要小。
那么最小生成树很好理解了,所有可能的生成树中,权重和最小的那棵生成树就叫「最小生成树」。
PS:一般来说,我们都是在无向加权图中计算最小生成树的,所以使用最小生成树算法的现实场景中,图的边权重一般代表成本、距离这样的标量。
这里需要使用Union-Find 并查集算法,来保证图中生成的是树(不包环)。
并查集算法是如何做到的?先来看看这道题:
给你输入编号从 0 到 n - 1 的 n 个结点,和一个无向边列表 edges(每条边用节点二元组表示),请你判断输入的这些边组成的结构是否是一棵树。

这些边构成的是一颗树,应该返回true:

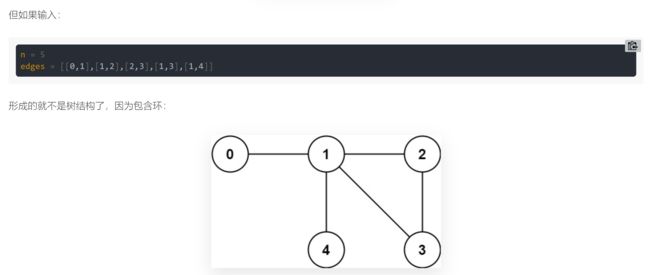
对于这道题,我们可以思考一下,什么情况下加入一条边会使得树变成图(出现环)?
显然,像下面这样添加边会出现环:
而判断两个节点是否连通(是否在同一个连通分量中)就是 Union-Find 算法的拿手绝活,所以这道题的解法代码如下:
// 判断输入的若干条边是否能构造出一棵树结构
boolean validTree(int n, int[][] edges) {
// 初始化 0...n-1 共 n 个节点
UF uf = new UF(n);
// 遍历所有边,将组成边的两个节点进行连接
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
// 若两个节点已经在同一连通分量中,会产生环
if (uf.connected(u, v)) {
return false;
}
// 这条边不会产生环,可以是树的一部分
uf.union(u, v);
}
// 要保证最后只形成了一棵树,即只有一个连通分量
return uf.count() == 1;
}
class UF {
// 见上文代码实现
}
在这个最小生成树构造的过程中,就可以实现一些值的计算和统计。
Kruskal 算法
所谓最小生成树,就是图中若干边的集合(我们后文称这个集合为 mst,最小生成树的英文缩写),你要保证这些边:
1、包含图中的所有节点,就是整个图的连通分量 = 1(全部节点连起来了)
2、形成的结构是树结构(即不存在环),就是用并查集的connected函数查看是否连通(相同根节点)。
3、权重和最小。
有之前题目的铺垫,前两条其实可以很容易地利用 Union-Find 算法做到,关键在于第 3 点,如何保证得到的这棵生成树是权重和最小的?
这里就用到了贪心思路:
将所有边按照权重从小到大排序,从权重最小的边开始遍历,如果这条边和mst中的其它边不会形成环,则这条边是最小生成树的一部分,将它加入mst集合;否则,这条边不是最小生成树的一部分,不要把它加入mst集合。
最低成本联通所有城市(中等)
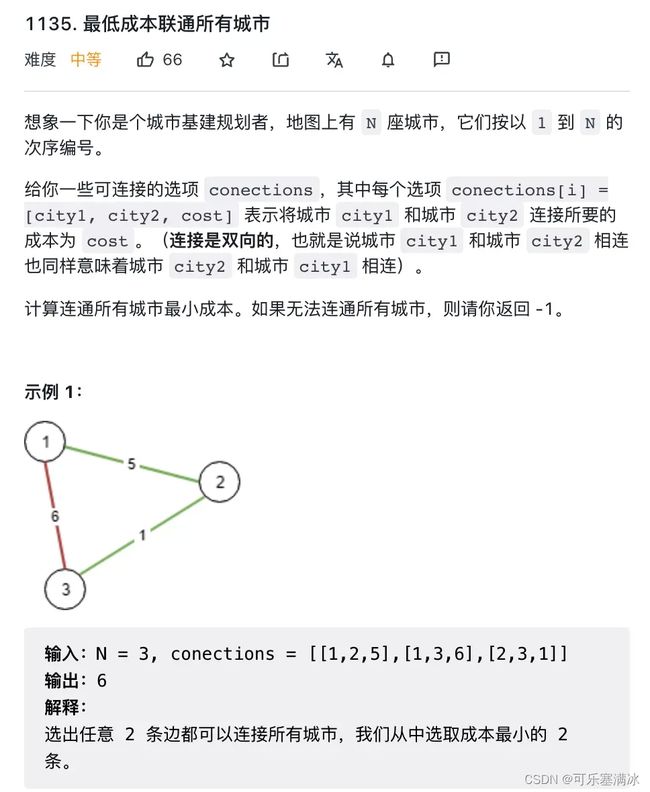
就是找最小生成树!每座城市相当于图中的节点,连通城市的成本相当于边的权重,连通所有城市的最小成本即是最小生成树的权重之和。
二维数组的排序(选择第几个元素为排序依据)
int[][] nums = new int[][]{{1,4,5},{2,3,5},{7,8,5}};
// 按照0 1 2,第2个元素排序,从小到大
// 如果第2个元素相同,那就按第1个元素排序
Arrays.sort(nums, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if (o1[2] == o2[2]) {
// 按第1个元素排序(默认从小到大)
return o1[1] - o2[1];
} else {
return o1[2] - o2[2];
}
}
});
class Solution {
int minimumCost(int n, int[][] connections) {
// 城市编号 1...n,所以初始化大小为n + 1
UF uf = new UF(n + 1);
// 对所有边按权重排序
Arrays.sort(connections, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
// 记录最小生成树的权重之和
int mst = 0;
for (int[] edge : connections) {
int u = edge[0];
int v = edge[1];
int weight = edge[2];
// 如果这条边会产生环,则不能加入mst
if (uf.connected(u, v)) {
continue;
}
// 如果不会产生环,那就可以加入mst,属于最小生成树
mst += weight;
uf.union(u, v);
}
// 保证所有节点被连通,就是连通分量count = 1
// 但是由于题目下标从1开始,节点0自身就是独立的
// 所以count应该=2
return uf.count() == 2 ? mst : -1;
}
}
class UF {
// 连通分量个数
int count;
// 每棵树
int[] parent;
// 每棵树的节点数
int[] size;
UF(int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
// 图中的每个节点指向自己
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 找根节点
public int find(int x) {
while (parent[x] != x) {
// 路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
// 判断是否连通
public boolean connected(int p, int q) {
return find(p) == find(q);
}
// 连通两个节点
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
// 本来就联通
if (rootQ == rootP) return;
if (size[rootP] > size[rootQ]) {
// 小树接在大树后
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
// 连通分量--
count--;
}
// 返回连通分量个数
public int count() {
return count;
}
}
有了上面的代码,可以发现,并查集也可以用于无向图中环的检测。
总结下这种题目的思路,一般需要连接所有点(满足最小生成树的定义),需要按照某种费用、花销、开销等来连通所有点。处理方法:按照题目意思,构建图-边,然后将边按照某种意义排序(保证所谓的最小费用),最后用并查集连接边,如果连接这条边会产生环(就是connected = true),那就不连,否则就连。
连接所有点的最小费用(中等)
points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
算法应该返回 20,按如下方式连通各点:

很显然这也是一个标准的最小生成树问题:每个点就是无向加权图中的节点,边的权重就是曼哈顿距离,连接所有点的最小费用就是最小生成树的权重和。
本题相当于把边的权重换一种方式进行告诉。
class Solution {
int minCostConnectPoints(int[][] points) {
int n = points.length;
// 生成所有边和权重
List<int[]> edges = new ArrayList<>();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int xi = points[i][0], yi = points[i][1];
int xj = points[j][0], yj = points[j][1];
// 添加边、权重
edges.add(new int[] {
i, j, Math.abs(xi - xj) + Math.abs(yi - yj)
});
}
}
// 将边按照权重从小到大排序
Collections.sort(edges, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
// 执行Kruskal算法
int mst = 0;
UF uf = new UF(n);
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
int weight = edge[2];
// 如果这条边会产生环,就不能加入mst
if (uf.connected(u, v)) {
continue;
}
// 不会产生环,就属于最小生成树
mst += weight;
uf.union(u, v);
}
return mst;
}
}
// UF类实现见上文代码
可以看出,最小生成树算法的题目,都会在题目中告知,连接所有点、所有城市等,最小生成树就是能够保障连通所有节点的代价最小。
1142 繁忙的都市(简单)
城市C是一个非常繁忙的大都市,城市中的道路十分的拥挤,于是市长决定对其中的道路进行改造。
城市C的道路是这样分布的:
城市中有 n 个交叉路口,编号是 1∼n,有些交叉路口之间有道路相连,两个交叉路口之间最多有一条道路相连接。
这些道路是 双向 的,且把所有的交叉路口直接或间接的连接起来了。
每条道路都有一个分值,分值越小表示这个道路越繁忙,越需要进行改造。
但是市政府的资金有限,市长希望进行改造的道路越少越好,于是他提出下面的要求:
1.改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
2.在满足要求1的情况下,改造的道路尽量少。
3.在满足要求1、2的情况下,改造的那些道路中分值最大值尽量小。
作为市规划局的你,应当作出最佳的决策,选择哪些道路应当被修建。
输入格式
第一行有两个整数 n,m 表示城市有 n 个交叉路口,m 条道路。
接下来 m 行是对每条道路的描述,每行包含三个整数u,v,c 表示交叉路口 u 和 v 之间有道路相连,分值为 c。
输出格式
两个整数 s,max,表示你选出了几条道路,分值最大的那条道路的分值是多少。
数据范围
1≤n≤300,
1≤m≤8000,
1≤c≤10000
输入样例
4 5
1 2 3
1 4 5
2 4 7
2 3 6
3 4 8
输出样例
3 6
1.改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
2.在满足要求1的情况下,改造的道路尽量少。
3.在满足要求1、2的情况下,改造的那些道路中分值最大值尽量小。
上面的这三个要求就是对最小生成树的诠释,最小生成树就是选择最少的道路、且花费最小进行连接,直接用最小生成树算法写就行。
import java.util.*;
import java.io.*;
public class Main {
static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
public static void main(String[] args) throws IOException {
String[] input = reader.readLine().trim().split(" ");
int n = Integer.parseInt(input[0]);
int k = Integer.parseInt(input[1]);
List<int[]> edges = new LinkedList<>();
while (k-- > 0) {
input = reader.readLine().trim().split(" ");
int u = Integer.parseInt(input[0]);
int v = Integer.parseInt(input[1]);
int w = Integer.parseInt(input[2]);
edges.add(new int[] {u,v,w});
}
Collections.sort(edges, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
// 分值最大最小
// 选出的道路条数
int mst = 0;
int cnt = 0;
UF uf = new UF(n + 1); // 1-n
for(int[] cur : edges) {
if (!uf.connected(cur[0], cur[1])) {
cnt++;
mst = cur[2];
uf.union(cur[0], cur[1]);
}
}
System.out.println(cnt + " " + mst);
}
}
class UF {
int count;
int[] size;
int[] parent;
UF (int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
for (int i = 0; i < n; i++) {
this.size[i] = 1;
this.parent[i] = i;
}
}
int find(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
boolean connected(int p, int q) {
return find(p) == find(q);
}
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
int getCount() {
return count;
}
}
1143 联络员
- 问题描述:
Tyvj已经一岁了,网站也由最初的几个用户增加到了上万个用户,随着Tyvj网站的逐步壮大,管理员的数目也越来越多,现在你身为Tyvj管理层的联络员,希望你找到一些通信渠道,使得管理员两两都可以联络(直接或者是间接都可以)。本题中所涉及的通信渠道都是双向的。Tyvj是一个公益性的网站,没有过多的利润,所以你要尽可能的使费用少才可以。目前你已经知道,Tyvj的通信渠道分为两大类,一类是必选通信渠道,无论价格多少,你都需要把所有的都选择上;还有一类是选择性的通信渠道,你可以从中挑选一些作为最终管理员联络的通信渠道。数据保证给出的通信渠道可以让所有的管理员联通。注意: 对于某两个管理员 u,v,他们之间可能存在多条通信渠道,你的程序应该累加所有 u,v 之间的必选通行渠道。
输入格式
第一行两个整数 n,m 表示Tyvj一共有 n 个管理员,有 m 个通信渠道;第二行到 m + 1 行,每行四个非负整数,p,u,v,w 当 p = 1 时,表示这个通信渠道为必选通信渠道;当 p = 2 时,表示这个通信渠道为选择性通信渠道;u,v,w 表示本条信息描述的是 u,v 管理员之间的通信渠道,u 可以收到 v 的信息,v 也可以收到 u 的信息,w 表示费用。
输出格式
一个整数,表示最小的通信费用。
数据范围
1 ≤ n ≤ 2000
1 ≤ m ≤ 10000
输入样例:
5 6
1 1 2 1
1 2 3 1
1 3 4 1
1 4 1 1
2 2 5 10
2 2 5 5
输出样例:
9
这道题也属于是最小生成树中常见的问题,要求必须选择一些边,在此基础上再构造最小生成树。
对于必须选的边,那就不管是否连通、有环,直接加入并查集中;对于非必选的边,先存储下来,然后再去做Kruskal算法。
import java.util.*;
import java.io.*;
import java.util.List;
public class Main {
static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
public static void main(String[] args) throws IOException {
String[] input = reader.readLine().trim().split(" ");
int n = Integer.parseInt(input[0]);
int m = Integer.parseInt(input[1]);
// 存储可选信道
List<int[]> edges = new LinkedList<>();
// n个管理员:1-n
UF uf = new UF(n + 1);
int mst = 0;
while (m-- > 0) {
input = reader.readLine().trim().split(" ");
int p = Integer.parseInt(input[0]);
int u = Integer.parseInt(input[1]);
int v = Integer.parseInt(input[2]);
int w = Integer.parseInt(input[3]);
if (p == 1) {
// 必选信道,先加入到生成树中
uf.union(u, v);
mst += w;
} else {
// 非必选信道,先存起来
edges.add(new int[] {u, v, w});
}
}
// 针对非必选信道,做最小生成树
Collections.sort(edges, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
for (int[] cur : edges) {
if (!uf.connected(cur[0], cur[1])) {
mst += cur[2];
uf.union(cur[0], cur[1]);
}
}
System.out.println(mst);
}
}
class UF {
int count;
int[] size;
int[] parent;
UF (int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
for (int i = 0; i < n; i++) {
this.size[i] = 1;
this.parent[i] = i;
}
}
int find(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
boolean connected(int p, int q) {
return find(p) == find(q);
}
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
int getCount() {
return count;
}
}
1144 连接格点
import java.util.*;
import java.io.*;
import java.util.List;
public class Main {
static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
public static void main(String[] args) throws IOException {
String[] input = reader.readLine().trim().split(" ");
int m = Integer.parseInt(input[0]);
int n = Integer.parseInt(input[1]);
int[][] ids = new int[m + 1][n + 1]; // 完成id的映射
int id = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
ids[i][j] = id++;
}
}
// 1 - m * n
UF uf = new UF(m * n + 1);
// 已经存在的边
input = reader.readLine().trim().split(" ");
int ax = Integer.parseInt(input[0]);
int ay = Integer.parseInt(input[1]);
int bx = Integer.parseInt(input[2]);
int by = Integer.parseInt(input[3]);
int p1 = ids[ax][ay];
int p2 = ids[bx][by];
if (p1 < p2) {
uf.union(p1, p2);
} else {
uf.union(p2, p1);
}
// 记录边
List<int[]> edges = new LinkedList<>();
int[] xx = new int[] {1, -1, 0, 0};
int[] yy = new int[] {0, 0, -1, 1};
// 遍历点阵,计算相邻两点点对
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 二维降一维,获得点的映射关系
int u = ids[i][j];
for (int k = 0; k < 4; k++) {
int tx = xx[k] + i;
int ty = yy[k] + j;
if (tx <= 0 || ty <= 0 || tx > m || ty > n) continue;
int v = ids[tx][ty];
if (k == 0 || k == 1) {
// 上下花费1
// 避免重复记录
if (u < v) {
edges.add(new int[] {u, v, 1});
}
} else {
// 左右花费2
// 避免重复记录
if (u < v) {
edges.add(new int[] {u, v, 2});
}
}
}
}
}
Collections.sort(edges, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
int mst = 0;
for (int[] cur : edges) {
if (!uf.connected(cur[0], cur[1])) {
uf.union(cur[0], cur[1]);
mst += cur[2];
}
}
System.out.println(mst);
}
}
class UF {
int count;
int[] parent;
int[] size;
UF (int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
for (int i = 0; i < n; i++) {
this.parent[i] = i;
this.size[i] = 1;
}
}
int find(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
boolean connected(int p, int q) {
return find(p) == find(q);
}
void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
int getCount() {
return count;
}
}
三、Dijkstra 算法框架
首先,我们先看一下 Dijkstra 算法的签名:
// 输入一幅图和一个起点 start,计算 start 到其他节点的最短距离
int[] dijkstra(int start, List<Integer>[] graph);
// 输出一个记录最短路径权重的数组
其次,我们也需要一个 State 类来辅助算法的运行:
class State {
// 图节点的 id
int id;
// 从 start 节点到当前节点的距离
int distFromStart;
State(int id, int distFromStart) {
this.id = id;
this.distFromStart = distFromStart;
}
}
无权图和有权图中的BFS区别
-
普通 BFS 算法中,根据 BFS 的逻辑和无权图的特点,第一次遇到某个节点所走的步数就是最短距离,所以用一个 visited 数组防止走回头路,每个节点只会经过一次。
搜索算法中,找最小步数也是用BFS算法,因为它可以保证第一次到达的就是最小的步数。 -
加权图中的 Dijkstra 算法和无权图中的普通 BFS 算法不同,在 Dijkstra 算法中,你第一次经过某个节点时的路径权重,不见得就是最小的(这也好理解,BFS只看节点,不会关注权重),所以对于同一个节点,我们可能会经过多次,而且每次的 distFromStart 可能都不一样,所以不会使用visited数组防止走回头路,因为需要走回头路,比如下图:
我会经过节点 5 三次,每次的 distFromStart 值都不一样,那我取 distFromStart 最小的那次,不就是从起点 start 到节点 5 的最短路径权重了么?
好了,明白上面的几点,我们可以来看看 Dijkstra 算法的代码模板。
其实,Dijkstra 可以理解成一个带 dp table(或者说备忘录)的 BFS 算法,伪码如下:
class State {
// 图节点的id
int id;
// 从 start 节点到当前节点的距离
int distFromStart;
State(int id, int distFromStart) {
this.distFromStart = distFromStart;
this.id = id;
}
}
// 返回节点 from 到节点 to 之间的边的权重(看实际情况,可能也不需要)
int weight(int from, int to);
// 输入节点 s 返回 s 的相邻节点(看实际情况,可能也不需要)
List<Integer> adj(int s);
// 输入一幅图和一个起点 start,计算 start 到其他节点的最短距离
int[] dijkstra(int start, List<Integer>[] graph) {
// 图中节点的个数
int V = graph.length;
// 记录最短路径的权重,你可以理解为 dp table
// 定义:distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重
int[] distTo = new int[V];
// 求最小值,所以 dp table 初始化为正无穷
Arrays.fill(distTo, Integer.MAX_VALUE);
// base case,start 到 start 的最短距离就是 0
distTo[start] = 0;
// 优先级队列,distFromStart 较小的排在前面
// 普通的链表也可以,使用预先队列是为了提高效率
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.distFromStart - b.distFromStart;
});
// 从起点 start 开始进行 BFS
pq.offer(new State(start, 0));
while (!pq.isEmpty()) {
State curState = pq.poll();
int curNodeID = curState.id;
int curDistFromStart = curState.distFromStart;
// 存在更短路径,那就continue
if (curDistFromStart > distTo[curNodeID]) {
// 已经有一条更短的路径到达 curNode 节点了
continue;
}
// 将 curNode 的相邻节点装入队列
for (int nextNodeID : adj(curNodeID)) {
// 看看从 curNode 达到 nextNode 的 “权值和” (距离)是否会更短
int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
// 从起点经过 curNode 达到 nextNode的 “权值和” 更短,那就需要更新
if (distTo[nextNodeID] > distToNextNode) {
// 更新 dp table
distTo[nextNodeID] = distToNextNode;
// 将这个节点以及距离放入队列
pq.offer(new State(nextNodeID, distToNextNode));
}
}
}
return distTo;
}
上面的代码会计算出start起点,到任意节点的最短路径,返回结果为数组distTo,distTo[2]就是起点start到第2个节点的最短路径。
学习自:https://labuladong.gitee.io/algo/2/19/43/
对比普通的 BFS 算法,你可能会有以下疑问:
1、跟回溯算法中的BFS算法相比,这里的BFS没有 visited 集合记录已访问的节点,所以一个节点会被访问多次,会被多次加入队列,那会不会导致队列永远不为空,造成死循环?
2、为什么用优先级队列 PriorityQueue 而不是 LinkedList 实现的普通队列?为什么要按照 distFromStart 的值来排序?

这里需要说明的是,Dijkstra算法求解最短路径,只能求解非负权值的问题,如果有负权值(准确的说是负环),则不能够求解!
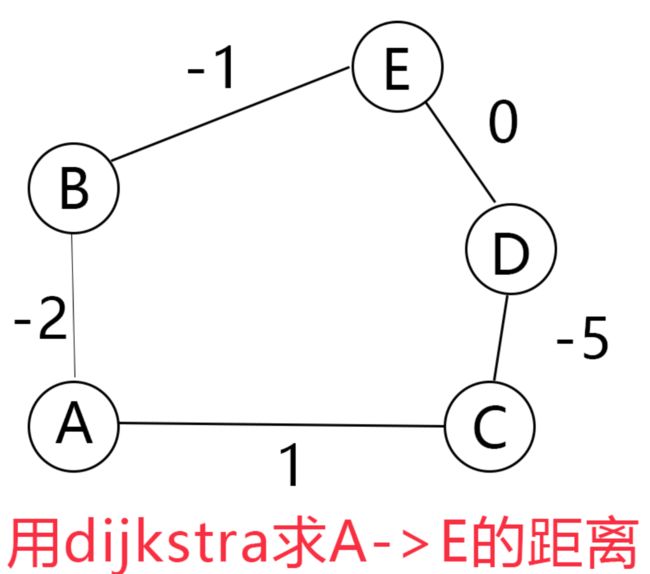
如果用dijkstra算法来计算最短路径,一定会出错。
因为按照dijkstra算法,它的原则是基于贪心进行查找,所以它的查找顺序应该是:BEDC。
造成的结果就是:找到第二个节点时,就会直接判断E的最短路径为-3.并且后续节点的查找也不会改变这个值。
但是显然,我们知道E的最短路径为-4.
出现这种情况的根本原因是,负环(含负值的环)出现。导致贪心的查找逻辑无法继续成立。用通俗的话来说,就是面对负权值的环时,算法在查找时容易”鼠目寸光“,很简单的下定结论。
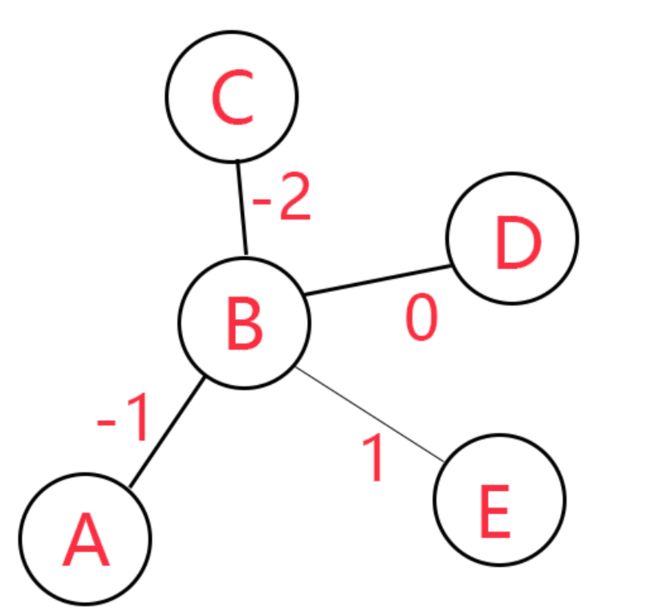
在这种情况下,djikstra算法就能正常工作,并且不受负权值影响。
它的查找顺序应该是:BCDE。而CD由于没有与E形成环,所以负权值就不再会破坏算法平衡,成为了一个表示大小的数字。
最后的结果显然是0.虽然这只是一个例子,但是我们可以很容易的想到,只要不出现负环,任何一个负权值图我们都可以用这种方法计算。
换而言之,dijkstra算法真正的问题是无法计算负环而不是负权值。所以我们也可以把它用在一些不出现负环的负权值问题上。
解决负环问题需要使用Bellman-Ford算法实现,注意!有些同学可能会想,通过偏移,使得权值全部大于0不就行了吗?这种想法是错误的,不能够解决负环的问题,不然也不会有专门的算法来解决负环问题。
3、如果我只想计算起点 start 到某一个终点 end 的最短路径,是否可以修改算法,提升一些效率?
// 输入起点 start 和终点 end,计算起点到终点的最短距离
int dijkstra(int start, int end, List<Integer>[] graph) {
// ...
while (!pq.isEmpty()) {
State curState = pq.poll();
int curNodeID = curState.id;
int curDistFromStart = curState.distFromStart;
// 在这里加一个判断就行了,其他代码不用改
if (curNodeID == end) {
return curDistFromStart;
}
if (curDistFromStart > distTo[curNodeID]) {
continue;
}
// ...
}
// 如果运行到这里,说明从 start 无法走到 end
return Integer.MAX_VALUE;
}
因为优先级队列自动排序的性质,每次从队列里面拿出来的都是 distFromStart 值最小的,所以当你第一次从队列中拿出终点 end 时,此时的 distFromStart 对应的值就是从 start 到 end 的最短距离。(相当于是实现普通BFS算法中,第一次到达终点的一定是距离最小的方案)
这个算法较之前的实现提前 return 了,所以效率有一定的提高。
网络延迟时间(中等)


需要注意的是,最后的答案应该是起点到所有顶点的最大的最短距离,这样才能保证所有的节点接收到信号。
class Solution {
public int networkDelayTime(int[][] times, int n, int k) {
// 先建图
List<int[]>[] graph = new LinkedList[n + 1];
// 也可以写成:
// List[] graph = new LinkedList[n];
// List数组记得对每一个List进行初始化,才能使用
// 注意节点从1开始,数组大小要开成:n + 1
for (int i = 1; i <= n; i++) {
graph[i] = new LinkedList<>();
}
for (int i = 0; i < times.length; i++) {
int from = times[i][0];
int to = times[i][1];
int weight = times[i][2];
// from -> List<(to, weight)>
// 邻接表存储图结构,同时存储权重信息weight
graph[from].add(new int[] {to, weight});
}
// 开始dijkstra算法,k为起点
int[] distTo = dijkstra(k, graph);
// 找到最长的那一条最短路径就是答案
int res = 0;
for (int i = 1; i < distTo.length; i++) {
if (distTo[i] == Integer.MAX_VALUE) {
// 有节点到达不了
return -1;
}
res = Math.max(res, distTo[i]);
}
return res;
}
// 类中类
class State {
// 图节点的id
int id;
// 从 start 节点到当前节点的最短路径
int distFromStart;
State(int id, int distFromStart) {
this.id = id;
this.distFromStart = distFromStart;
}
}
int[] dijkstra(int start, List<int[]>[] graph) {
// distTo[i],就是start到i节点的最短路径
// distTo也是需要返回的结果数组
int[] distTo = new int[graph.length];
Arrays.fill(distTo, Integer.MAX_VALUE);
// base case
distTo[start] = 0;
// 优先队列加快速度
Queue<State> pq = new PriorityQueue<>(new Comparator<State>() {
@Override
public int compare(State o1, State o2) {
// 更小的距离优先
return o1.distFromStart - o2.distFromStart;
}
});
// 起点入队
pq.offer(new State(start, 0));
while (!pq.isEmpty()) {
State tmp = pq.poll();
int curId = tmp.id;
int curDist = tmp.distFromStart;
// 当前节点的最短路径已经小于目前遍历的路径
if (curDist > distTo[curId]) {
continue;
}
// 遍历当前节点的相邻节点
// 存储结构是:graph[start]中存储了多个[to, weight]数组
for (int[] curNode : graph[curId]) {
int nextNode = curNode[0];
int weight = curNode[1];
// 更新最短路径
if (distTo[nextNode] > weight + curDist) {
distTo[nextNode] = weight + curDist;
pq.offer(new State(nextNode, weight + curDist));
}
}
}
return distTo;
}
}
鉴于Dijkstra最短路径算法不能处理负环问题,但作为一种经典算法,需要学习其基本思想和实现方法。更好的算法,更具有包容性的算法是SPFA(Shortest Path Faster Algorithm)
最短路径算法常常求的是一个distTo数组,它记录了起点到达任意点的最短路径,并不是单独只返回某个点到起点的最短路径。
※四、SPFA算法框架、负环判断方法
spfa就是BellmanFord的一种实现方式,其具体不同在于,对于处理松弛操作时,采用了队列(先进先出方式)操作,从而大大提高了时间复杂度。
大概思路和dijkstra相似但是又大有不同,这里队列里存放的不再是1.距离最近且2.未被使用这两个条件同时存在的点了,
而是只保留一个条件:未被使用的点!所以又需要多的一个used数组来存储每个点是否被使用。
从源点出发,将与其直接相连的点依次更新,并加入队列中(只有发生更新才会加入队列,防止陷入死循环,这点在之前Dijkstra算法里讲过原因),之后将刚刚用来更新其他节点的点从队列中抛出,并将其状态改为false。 之后一直判断到结束即可!
- 初始化处理,邻接表头数组h(初始化为-1 ),距离数组dist(初始化为无穷大)
- 将源点的序号加入队列中,dist[start] = 0,并将其使用状态(used)标记为true
- 在队列不为空的前提下,抛出表头元素,并将其使用状态(used)标记为false
- 用表头元素更新与它直接相连的点,若发生跟新则将其加入队列中,并将其使用状态(used)改为true
- 结束之后判断是否能够到达目标节点,若可以直接返回,不可以返回题目给定内容(一般是顺便判定负环)
SPFA的代码其实很类似BFS搜索
有负环,不可能有最短路径,因为会一直更新下去,Dijkstra不能检测负环,但是SPFA可以,这就是为什么更推荐SPFA算法的原因。
判断负环的方法:统计当前节点的最短路径包含的边的条数,如果 == n,就存在负环。
class Solution {
public int networkDelayTime(int[][] times, int n, int k) {
// 先建图
List<int[]>[] graph = new LinkedList[n + 1];
// 也可以写成:
// List[] graph = new LinkedList[n];
// List数组记得对每一个List进行初始化,才能使用
// 注意节点从1开始,数组大小要开成:n + 1
for (int i = 1; i <= n; i++) {
graph[i] = new LinkedList<>();
}
for (int[] time : times) {
int from = time[0];
int to = time[1];
int weight = time[2];
// from -> List<(to, weight)>
// 邻接表存储图结构,同时存储权重信息weight
graph[from].add(new int[]{to, weight});
}
// 记录开始节点到任一节点的最短路径
int[] distTo = new int[graph.length];
Arrays.fill(distTo, Integer.MAX_VALUE);
// 记录是否入队
boolean[] vis = new boolean[graph.length];
// 统计当前节点的遍历次数,用于判断负环
int[] nums = new int[graph.length];
// 初始条件
distTo[k] = 0;
vis[k] = true;
// 只有一个点,不含边
nums[k] = 0;
// 是否为负环
boolean flag = false;
// SPFA开始,k为起点
Queue<Integer> queue = new LinkedList<>();
queue.offer(k);
while (!queue.isEmpty()) {
int curId = queue.poll();
// 出队
vis[curId] = false;
// 遍历与该节点相邻的节点
for (int[] next : graph[curId]) {
int nextId = next[0];
int weight = next[1];
// 如果当前的更新距离更小才能更新
if (distTo[nextId] > distTo[curId] + weight) {
// 更新距离
distTo[nextId] = distTo[curId] + weight;
// 当前节点的最短路径包含的边数 + 1
nums[nextId] = nums[curId] + 1;
if (nums[nextId] == n) {
// 是负环
flag = true;
break;
}
// 如果队列中没有,就入队
if (vis[nextId] == false) {
vis[nextId] = true;
queue.offer(nextId);
}
}
}
// 是负环
if (flag) {
break;
}
}
// 是负环了
if (flag) {
return -1;
}
int res = 0;
for (int i = 1; i < graph.length; i++) {
if (distTo[i] == Integer.MAX_VALUE) {
return -1;
}
res = Math.max(res, distTo[i]);
}
return res;
}
}
上面的代码中,为了方便,没有使用State类,队列就是直接存储节点ID即可。
模板背不住?试试自己把这道题做5遍~ 注意分层次,建图代码、状态初始化代码、BFS实现SPFA代码。
需要注意的是,最小生成树和最短路径算法,它们对节点的存储是不一样的,最小生成树只统计边和权值,每次尝试去连通一条边。最短路径算法是以某个节点到其它的节点的边的存储,这样是为了方便能够遍历当前点的相邻点。
一直在说负环,下面就给一道负环的题目,就是模板题
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int t = scanner.nextInt();
while (t > 0) {
int n = scanner.nextInt();
int m = scanner.nextInt();
// 先建图
List<int[]>[] graph = new LinkedList[n + 1];
for (int i = 0; i < n + 1; i++) {
graph[i] = new LinkedList<>();
}
for (int i = 0; i < m; i++) {
int u = scanner.nextInt();
int v = scanner.nextInt();
int w = scanner.nextInt();
if (w < 0) {
graph[u].add(new int[] {v, w});
} else {
graph[u].add(new int[] {v, w});
graph[v].add(new int[] {u, w});
}
}
int[] distTo = new int[n + 1];
Arrays.fill(distTo, Integer.MAX_VALUE);
// 从顶点1出发
distTo[1] = 0;
boolean[] vis = new boolean[n + 1];
int[] nums = new int[n + 1];
Queue<Integer> queue = new LinkedList<>();
queue.add(1);
vis[1] = true;
nums[1] = 0;
boolean flag = false;
while (!queue.isEmpty()) {
int curId = queue.poll();
vis[curId] = false;
for (int[] node : graph[curId]) {
int to = node[0];
int weight = node[1];
if (distTo[to] > distTo[curId] + weight) {
distTo[to] = distTo[curId] + weight;
nums[to] = nums[curId] + 1;
if (nums[to] == n) {
flag = true;
break;
}
if (vis[to] == false) {
vis[to] = true;
queue.offer(to);
}
}
}
if (flag) {
break;
}
}
if (flag == false) {
System.out.println("NO");
} else {
System.out.println("YES");
}
t--;
}
}
}
博客又爆内存了,下面内容看图论算法四吧!







