【LeetCode75】第四十七题 迷宫中离入口最近的出口

目录

题目：

示例：

分析：

代码：

---

题目：

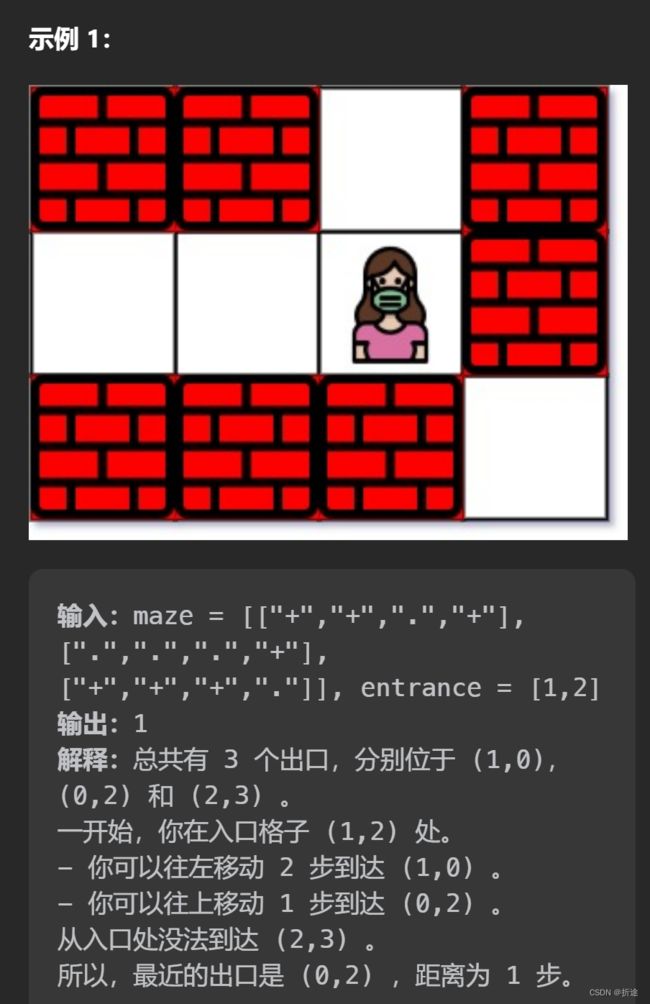
示例：

分析：

题目给我们一个数组形式的地图，让我们找出离入口最近的出口，出口就是地图的边界。

那么这道题可以使用DFS也可以BFS，不过DFS是暴力解法，需要把所有能走的路都走一边，所以会超时，因此我们只能使用BFS，BFS虽然也是暴力解法，不过我们要找的是最短路径，所以使用BFS一找到出口就可以直接返回路径长度，不需要把所有路都走一遍，所以比DFS要更快。

不过我这里就大概的把DFS和BFS都稍微讲一下。

DFS的话就是用的递归，每次都向四个方向再次递归，并且需要将地图中当前的位置重置为墙来避免重复递归到同一个地方，在递归中直到遇到墙就直接退出本次递归，或者是遇到了地图的边缘也就是到了出口，我们就记录一下路径，和答案的最短路径比较一下，更新为较小的值。

最后DFS完毕，我们将记录的最短路径返回即可，不过超时，因为DFS会遍历所有能从入口走到的地方。

而BFS是像辐射状向入口四周的能走的路开始扩散，BFS是使用队列来存每次要遍历的地方的，我们存进队列的是地点坐标以及路径长度的。

首先是将入口入队，入队的同时需要将地图中的入口位置置为墙，和上面DFS一样，为了避免重复 走同一条路。

 每次我们都将队列里的地点取出，接着向四个方向辐射，如果为墙则跳过，如果不为墙就判断一下是否为出口，为出口就直接把队列里取出的路径+1返回接口。否则就开始入队进入下一轮BFS，并且也是需要修改地图为墙。

最后直到队列为空，则表示我们BFS完毕，那么就是找不到出口，就返回-1就可以了。

总结一下，寻找有没有出口用DFS，寻找出口的最短路径用BFS。

代码：

class Solution {
public:
    //DFS
    int res=INT_MAX;
    void digui(vector>& maze,int x,int y,int time){
        if(time>=res || x<0||x>=maze.size()||y<0||y>=maze[0].size()||maze[x][y]=='+') return;
        if((x==0||x==maze.size()-1||y==0||y==maze[0].size()-1)&& time!=0){
            res=min(res,time);
            return;
        }
        maze[x][y]='+';
        digui(maze,x+1,y,time+1);
        digui(maze,x,y+1,time+1);
        digui(maze,x,y-1,time+1);
        digui(maze,x-1,y,time+1);
        maze[x][y]='.';
    }
    int nearestExit(vector>& maze, vector& entrance) {
        digui(maze,entrance[0],entrance[1],0);
        return res!=INT_MAX?res:-1;
    }

    //BFS
    int nearestExit(vector>& maze, vector& entrance) {
        int m = maze.size();
        int n = maze[0].size();
        // 上下左右四个相邻坐标对应的行列变化量
        vector dx = {1, 0, -1, 0};
        vector dy = {0, 1, 0, -1};
        queue> q;
        q.push({entrance[0], entrance[1], 0});  //入口入队
        maze[entrance[0]][entrance[1]] = '+';   //修改为墙避免重复走
        while (!q.empty()){  
            vectortemp = q.front();
            q.pop();
            // 遍历四个方向相邻坐标
            for (int k=0;k<4;k++){
                int newx = temp[0]+dx[k];
                int newy = temp[1]+dy[k];
                // 如果坐标不越界且并且不为墙
                if (newx >= 0 && newx < m && newy >= 0 && newy < n && maze[newx][newy] == '.'){
                    if (newx == 0 || newx == m - 1 || newy == 0 || newy == n - 1){  //如果走到了出口,那么返回
                        return temp[2] + 1;
                    }
                    q.push({newx, newy, temp[2]+1});    //新坐标入队
                    maze[newx][newy]='+';   //避免重复,修改为墙
                }
            }
        }
        return -1;
    }
};