【GAMES101】Lecture05,06 Rasterization 精要

本文图片来源于GAMES101课件。

注：本课程中所有变换都是建立在右手系的基础上的。

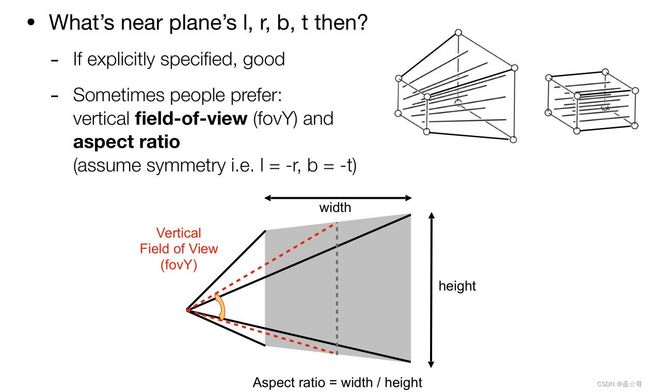
透视投影中的视锥

上一讲中我们知道，透视投影分为挤压(squish)与正交投影两步——前者将截锥体(frustum)压缩为以近平面为底面的长方体中(可以用6个参数$n,f,l,r,b,t$唯一确定)，后者再将长方体映射至中心为原点的$[-1,1{]}^3$标准立方体中。

截锥体可由视锥以及远近平面的深度$f,n$确定，而视锥需要以下两个参数确定：

1. 近平面的宽$w$和高$h$确定的纵横比(aspect ratio)：$aspect:=\frac{w}{h}$；

2. 垂直可视角(vertical field-of-view)：$fovY:=2\arctan \frac{h/2}{|n|}$。($n<0$)

注：垂直可视角也可以换成水平可视角，两者地位等价，只需确定其一即可推得另一。

视锥参数与长方体顶点坐标的转化

这里已经假定z轴垂直贯穿以近平面为底的长方体中心了，即$-l=r>0,-b=t>0$。

光栅化(Rasterization)

Raster == screen in German
Rasterize == drawing onto the screen

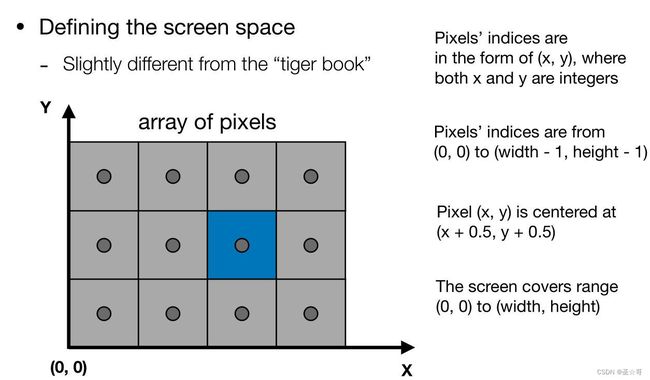
屏幕空间

从标准立方体(Canonical Cube)到XY屏幕(Screen)的变换——视口(Viewport)变换

屏幕是二维的，故变换与z方向无关，XY屏幕变换过程即从$[-1,1{]}^2$到$[0,width]\times [0,height]$，过程为先缩放，后平移左下角至$(0,0)$。尽管如此，该变换仍然是三维空间的变换，故变换矩阵仍是$4\times 4$的。

至此相当于已经摆好pose，准备按快门，但仍然还没有形成照片，接下来就是将屏幕所见的连续画面打碎成离散的像素(栅格)。

三角形网格

三角形具备一些优秀的性质使得它在图形学中运用广泛：

1. 边最少的多边形，其余多边形都可以由它组成；

2. 三角形一定构成一个平面，而不会出现扭曲；

3. 三角形内部定义非常明确，它一定是凸多边形，而凹多边形会出现一系列繁琐的问题；

4. 三角形内部任意位置的数值可以由三个顶点的数值计算获得（重心坐标系）。

用像素值近似投影至屏幕的三角形——采样(Sampling)

采样的定义：通常来说，函数的定义域连续(至少在我们感兴趣的范围内)，采样过程就是在定义域中选择一些离散的值作为输入，从而获得一系列离散的函数值(输出)。简单来说，采样就是连续到离散的过程。

基本流程：对于像素$(x,y)$的中心坐标$(x+0.5,y+0.5)$，判断其是否在三角形内部，若是，则将相应的值赋予位于$(x,y)$的像素。

需要考虑的问题：

1. 如何判断像素坐标点位于三角形内？—— 叉积；

2. 屏幕中所有像素都需要执行上述步骤吗？—— 不需要，用包围盒即可减少不必要的计算，比如AABB(Axis-Aligned Bounding Box)，可以取三角形顶点每个维度的最大最小值确定；

3. 存在性能瓶颈吗？—— 当然，比如又瘦又斜的三角形，可以记录每一行的左右像素范围，从而节约时间开销，这时候有其他的方法：

   

4. 能完美还原吗？ —— 不行，因为像素有大小，存在锯齿(Jaggies)，此现象又称为走样(aliasing)，后面将会着重解决它；

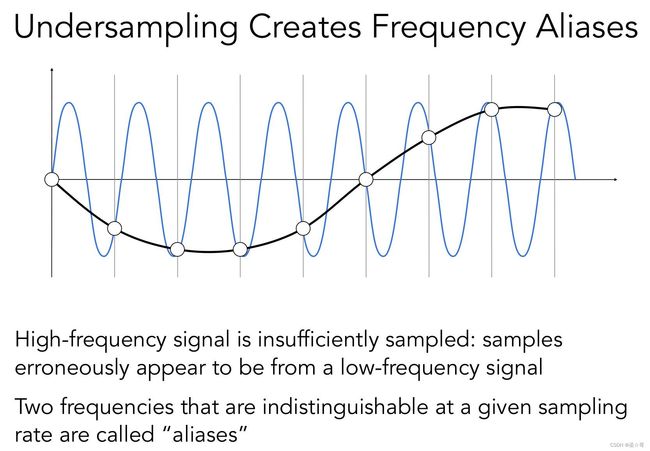
走样(aliasing)与反走样(antialiasing)

采样的一些问题以及原因：

① 锯齿；② 摩尔纹(欠采样)；③ 车轮效应(高速行驶下车轮出现逆时针转动)。

前两个问题是空间上的，第三个是时间上的。导致它们的原因在于信号的频率太高，但采样频率过低。

走样的定义：给定的一系列采样点存在多种不同频率的信号完美符合它，导致采样点看起来是来自低频信号的现象，通常原因是欠采样。

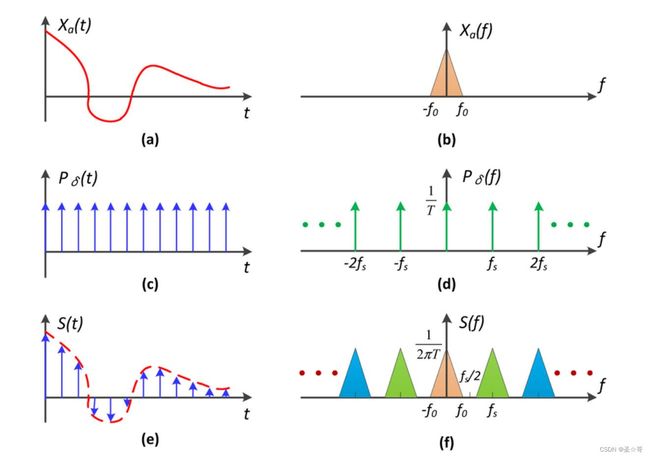
这里还讲了从时/空间域到频域的变换(Fourier Transform)以及逆变换(Fourier Inverse Transform)、滤波、卷积等数字图像处理相关的内容，这里只需知道画面主体是低频信号，画面细节(比如轮廓等)是高频信号，所谓模糊即滤去高频信号。

了解卷积定理的结论：空间域的卷积等价于频域的乘积，反过来，频域的卷积也等价于空间域的乘积。


Sampling is equivalent to “Repeating frequency contents”.

Aliasing is equivalent to “Mixed frequency contents”.

采样稀疏，对应采样频率就低，因而复制时更可能出现交错而导致走样。

反走样策略1：增加采样率

增加采样率，在频域上相当于把重复部分之间的距离增大，因而需要提高物理设备的分辨率。然而对于反走样策略来说，不可能对同一个设备进行这种改变，而且就算能更换，代价也比较大，故于此不作过多讨论。

反走样策略2：对信号进行模糊，然后采样

对于部分出现在一个像素格内的三角形，可以按照其在像素格中的面积占比来进行采样。

SSAA(Super-Sample Anti-Aliasing)，即超级采样抗锯齿，原理是在一个像素格内再细分多个采样点(2x2)，判断这些采样点是否位于三角形中，然后将它们的值进行加和平均，这里相当于提高了采样率。MSAA(Multi-Sample Anti-Aliasing)，即多重采样抗锯齿，与SSAA有所区别，性能有所优化，但也带来了一些问题。

一位博主对SSAA和MSAA总结得很不错，点此查看。

另外，FXAA和TAA有时间了解一下，还有DLSS，这些在商业中均有应用。

Visibility / Occlusion

Painter’s Algorithm vs. Z-Buffer

Painter’s Algorithm，即按照z深度从远到近对各三角形进行排序(由于深度是负的，故按z值从小到大排序)，然后从远到近的顺序对绘制三角形(overwrite)，但是这样可能存在unsolvable case：即多个三角形可能“盘”在一块，如下图示：

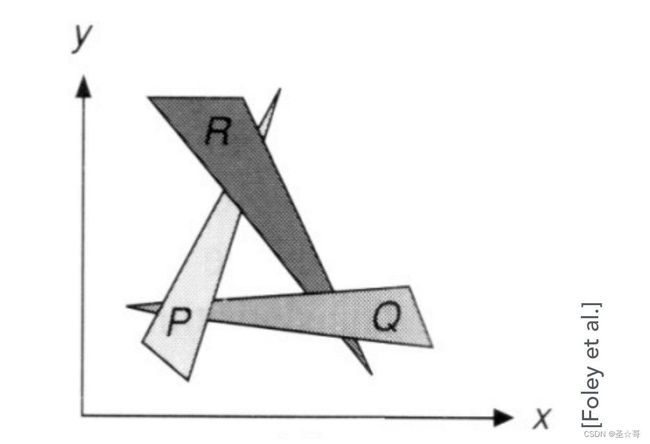
这样，画家算法就失效了。实际上，我们的最终目标并不是确定各三角形的先后顺序，而是确定每一个像素最终绘制什么。

Z-Buffer算法正是从每个像素来考虑，记录每一个像素当前最近的深度——因为每一格像素绘制的一定是深度最近的像素，不论它来自哪一个三角形。

算法伪代码：

复杂度：$O(n)$, $n$为三角形个数。

对算法的说明：

1. z这里相当于取了绝对值，即全为正；

2. 实际上操作的单元不一定是像素，可能是像素内的采样点。

局限(or 疑惑)：

1. 对于同一位置深度相同的三角形像素，Z-Buffer没有给出处理方案，本课程没有讨论该情况的解决办法；

2. Z-Buffer处理不了透明物体；

3. 对于一个像素格，可能存在多个深度不同的三角形出现在该像素格中，这种情况如何处理，是只绘制深度最近的三角形像素吗？（若有知道的大佬，可以在评论区留言）

笔者水平有限，若总结存有不妥之处，恳请各位大佬们批评指正~