算法训练Day06|哈希表part01(LeetCode242.有效的字母异位词、LeetCode349. 两个数组的交集、LeetCode202. 快乐数、LeetCode1. 两数之和)

文章讲解
视频讲解

哈希表的理论

哈希表是根据关键码的值而直接进行访问的数据结构。数组就是一种哈希表，通过数组的所以索引下标访问数组中的元素。哈希表可以很快地判断一个元素是否出现。
哈希函数把元素映射为哈希表上的索引。

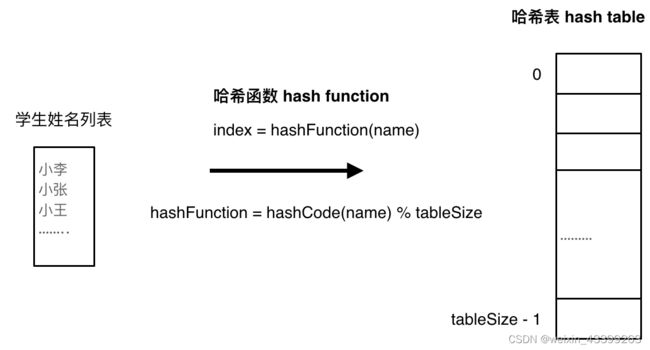
如果元素个数dataSize大于tableSize，就会出现哈希碰撞，多个元素使用一个索引值。一般有两种方法解决：一是拉链法，在碰撞位置建立链表；二是线性探测法，要求tableSize大于dataSize，有空余位置存放冲突数据。
哈希结构：

• 数组
• set （集合）
• map(映射)

集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::set	红黑树	有序	否	否	O(log n)	O(log n)
std::multiset	红黑树	有序	是	否	O(logn)	O(logn)
std::unordered_set	哈希表	无序	否	否	O(1)	O(1)

映射	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::map	红黑树	key有序	key不可重复	key不可修改	O(logn)	O(logn)
std::multimap	红黑树	key有序	key可重复	key不可修改	O(log n)	O(log n)
std::unordered_map	哈希表	key无序	key不可重复	key不可修改	O(1)	O(1)

对比后可以发现两张表是一样的，可以一起记。注意底层实现是红黑树的，key是有序的，但不能更改，否则会导致整棵树的错乱。
当我们遇到了要快速判断集合里一个元素是否出现过的时候，就要考虑哈希法。

242.有效的字母异位词

题目链接
给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1: 输入: s = “anagram”, t = “nagaram” 输出: true
示例 2: 输入: s = “rat”, t = “car” 输出: false
说明: 你可以假设字符串只包含小写字母。

重点

数据量比较小的用数组，要有key值的用map。
a到z总共26个字母，建立一个数组，统计字符串里各个字母出现的次数。遍历第一个数组，出现过就++，遍历第二个数组，出现过就–，,判断此时数组是否每个元素为0。

代码

注意代码中a-z和record下标0-25建立联系的方式。

class Solution {
public:
    bool isAnagram(string s, string t) {
        vector<int> record(26,0);
        for(int i=0;i<s.size();i++){          
            record[s[i]-'a']++;
        }
        for(int i=0;i<t.size();i++){
            record[t[i]-'a']--;
        }
        for(int i=0;i<26;i++){
            if(record[i]!=0) return false;
        }
        return true;
    }
};

349. 两个数组的交集

题目链接
题意：给定两个数组，编写一个函数来计算它们的交集。

说明： 输出结果中的每个元素一定是唯一的。 我们可以不考虑输出结果的顺序。

重点

这道题元素的大小是没有规定的，而且很分散，不适合使用数组。而且还强调了结果是唯一的，也就是去重的。std::set和std::multiset底层实现都是红黑树，std::unordered_set的底层实现是哈希表，unordered_set 效率是最高的，不需要对数据排序，而且去重。

代码

set.end()是最后一个元素的下一位，set.find(elem)如果没有找到就返回set.end()。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        vector<int> result;
        unordered_set<int> set_nums1(nums1.begin(),nums1.end());
        unordered_set<int> set_nums2(nums2.begin(),nums2.end());
        for(int num:set_nums2){
            if(set_nums1.find(num)!=set_nums1.end()){
                result.push_back(num);
            }
        }
        return result;
    }
};

202. 快乐数

题目链接
「快乐数」 定义为：
对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。如果这个过程 结果为 1，那么这个数就是快乐数。

示例：
输入：19
输出：true
解释：
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1

重点

• 熟悉取数值各个位上的单数操作。
• 平方和无限循环是终止运算的条件。建立unordered_set，来收集每次的平方和，如果出现过了，则说明平方和无限循环了。

代码

class Solution {
public:
    int getsum(int n){
        int sum=0;
        while(n){
            sum+=(n%10)*(n%10);
            //`n/10;` 不会修改 `n` 的值,正确更新“n”的值应该是“n /= 10;”
            n/=10;
        }
        return sum;
    }
    bool isHappy(int n) {
        unordered_set<int> s;
        while(1){
            int sum=getsum(n);
            if(sum==1) return true;
            if(s.find(sum)==s.end()){
                s.insert(sum);
            }
            else return false;
            //第一次写忘了这个，导致n没有更新
            n=sum;
        }
    }
};

1. 两数之和

题目链接
给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例:

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9

所以返回 [0, 1]

重点

• 为什么用哈希法？
  需要一个集合来存放我们遍历过的元素，然后在遍历数组的时候去询问这个集合，某元素是否遍历过，也就是 是否出现在这个集合。
• 为什么用unordered_map？
  不仅要知道元素有没有遍历过，还要知道这个元素对应的下标，std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。这道题目中并不需要key有序，选择unordered_map 效率更高。
• map存放什么？
  map目的用来放访问过的元素，map中的存储结构为 {key：数据元素，value：数组元素对应的下标}。
• 为什么把元素放key？
  在map中，排序是按照key值排的，map自带的find方法也是按着key值查找的，判断元素是否出现，这个元素就要作为key。
  用find函数来定位数据出现位置，它返回的一个迭代器，找到了，返回数据所在位置的迭代器，没找到，返回end函数的迭代器，

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> map;
        for(int i=0;i<nums.size();i++){
            //也可以unordered_map::iterator it;
            auto it=map.find(target-nums[i]);
            if(it!=map.end()){  
                return {it->second,i};   
            }
            //写成 
            //map.insert(pair(target-nums[i],i));   
            map.insert(pair<int,int>(nums[i],i));  
        }
        return {}; 
    }
};