提升方法与集成学习(学习笔记)
提升方法与集成学习
-
- 一.Boosting
- 二..AdaBoost、
-
- 1.简介
- 2.基本原理
- 3.弱分类器
- 4.Adaboost数据权重
- 三.提升树
- 四.RF随机森林
-
- 4.1 bagging的原理
- 4.2 随机森林
一.Boosting
Boosting,也称为增强学习或提升法,是一种重要的集成学习技术,能够将预测精度仅比随机猜度略高的弱学习器增强为预测精度高的强学习器,这在直接构造强学习器非常困难的情况下,为学习算法的设计提供了一种有效的新思路和新方法。作为一种元算法框架,Boosting几乎可以应用于所有目前流行的机器学习算法以进一步加强原算法的预测精度,应用十分广泛,产生了极大的影响。
这里我们不过多讲Boosting,下面我们来说一说其中最成功的代表AdaBoost
二…AdaBoost、
1.简介
上面我们说了Boosting,而AdaBoost正是其中最成功的代表,被评为数据挖掘十大算法之一。在AdaBoost提出至今的十几年间,机器学习领域的诸多知名学者不断投入到算法相关理论的研究中去,扎实的理论为AdaBoost算法的成功应用打下了坚实的基础。AdaBoost的成功不仅仅在于它是一种有效的学习算法,还在于1)它让Boosting从最初的猜想变成一种真正具有实用价值的算法;2)算法采用的一些技巧,如:打破原有样本分布,也为其他统计学习算法的设计带来了重要的启示;3)相关理论研究成果极大地促进了集成学习的发展。
2.基本原理
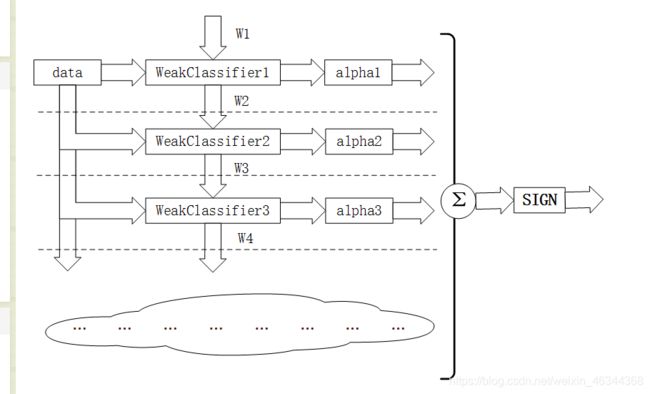
Adaboost算法基本原理就是将多个弱分类器(弱分类器一般选用单层决策树)进行合理的结合,使其成为一个强分类器。
Adaboost采用迭代的思想,每次迭代只训练一个弱分类器,训练好的弱分类器将参与下一次迭代的使用。所以说我们迭代了多少次就有多少个弱分类器。例如我们进行了N次迭代,这时就有N个弱分类器,在我们进行第N轮迭代时需要注意此时有N-1个弱分类器是已经训练好的,其参数不会再改变,本次我们训练的就是第N个分类器。
这些弱分类器间的关系:第N个弱分类器更可能分对前N-1个弱分类器没分对的数据,最终分类输出要看这N个分类器的综合效果。
3.弱分类器
Adaboost一般使用单层决策树作为其弱分类器。前面我们提到过决策树,而单层决策树就是其最简化的版本,只有一个决策点。因此,就算训练数据有多维特征,也只能选择其中一维特征来做决策,此时我们还需注意一个关键的问题,那就是决策的阈值。

举个例子:

若特征只有一个维度:我们可以选7或13为决策点
以7为决策点时:<7为一类,标记为+1;>=7为一类,标记为-1
以13为决策点时:<=13为一类,标记为-1;>13为一类,标记为+1
在单层决策树中,一共只有一个决策点,所以这两个决策点不能同时选取。
同理特征有两个维度时:

可以将纵坐标7作为决策点,决策方向是小于7分为+1类,大于(等于)7分类-1类。
也还可以将横坐标13作为决策点,决策方向是大于13的分为+1类,小于13的分为-1类。
同理,因为是单层决策树,我们也只能选取一个决策点,不可以同时选取两个。
以此类推:在更高维度也是大同小异的,我们主要需要记住两点:
-
在单层决策树中,只有一个决策点
-
我们要在其中一个维度中选择一个合适的决策阈值为决策点
4.Adaboost数据权重
我们所说的数据的权重主要用于弱分类器寻找其分类误差最小的点,在单层决策树计算误差时,Adaboost要求其乘上权重的,即计算带权重的误差。
举个例子:在以前没有权重时(其实是平局权重时),一共10个点时,对应每个点的权重都是0.1,分错1个,错误率就加0.1;分错3个,错误率就是0.3。现在,每个点的权重不一样了,还是10个点,权重依次是[0.01,0.01,0.01,0.01,0.01,0.01, 0.01,0.01,0.01,0.91],如果分错了第1一个点,那么错误率是0.01,如果分错了第3个点,那么错误率是0.01,要是分错了最后一个点,那么错误率就是0.91。此时我们在选择决策点时要尽可能把0.91这个点分对才能降低错误率。
由此可见,权重分布影响着单层决策树决策点的选择,权重大的点得到更多的关注,权重小的点得到更少的关注。
具体的一些例子大家可以去看看原文博主的文章,写得非常详细
参考链接:https://blog.csdn.net/px_528/article/details/72963977
三.提升树
提升树是以决策树为基分类器的提升方法,通常使用CART树。针对不同问题的提升树学习算法,主要区别在于使用的损失函数不同。
1.提升树算法:
提升树采用线性模型+前向分步算法+CART树(基函数)。提升树的加法模型可表示为:

所谓加法模型就是强分类器fM(x)可以由多个弱分类器T(x;Θ)线性相加
上图中M为树的个数,Θ表示决策树的参数
前面我们说了提升树针对不同的问题采用不同的损失函数。当基函数是分类树时,我们使用指数损失函数;当基函数是回归树,则使用平方误差损失函数。
分类提升树
对于基函数是分类树时,我们使用指数损失函数,此时正是AdaBoost算法的特殊情况,即将AdaBoost算法中的基分类器使用分类树即可。
回归提升树
我们将回归树的输入空间划分为R1,R2,…,RJ个区域,每个区域的输出分别为:Cj,则回归树可以表示为:

前向分步算法第m步的得到的模型为:
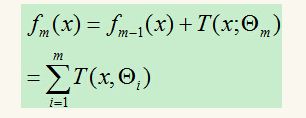
平方误差损失函数为:

设![]()
rm即为当前模型拟合数据的残差。对回归问题的提升树算法来说,只需简单地拟合当前模型的残差。
因为需要用到上一步的分类器,所以每轮都需要计算残差,然后遍历可能的切分点,找出平方损失函数最小的切分点将输入划分为两个子集,依次类推,直到不能继续划分。

参考链接1https://blog.csdn.net/mr_health/article/details/94335174
参考链接2https://www.cnblogs.com/liuwu265/p/4693113.html
四.RF随机森林
4.1 bagging的原理
bagging集成学习方法可以利用下图说明:
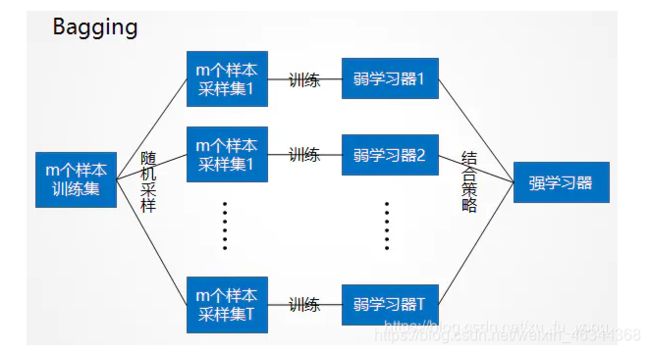
从上图可以看出bagging的特点在于“随机采样”。那么什么是随机采样呢?
随机采样(bootsrap)就是从我们的训练集里面采集固定个数的样本,但是每采集一个样本后,都将样本放回。也就是说,之前采集到的样本在放回后有可能继续被采集到。
对于bagging算法,一般采集的样本个数和训练的样本个数是一样多的,虽然个数相同但内容是不同的。如果我们对有m个样本训练集做T次的随机采样,则由于随机性,T个采样集各不相同。注意到这和GBDT的子采样是不同的。GBDT的子采样是无放回采样,而Bagging的子采样是放回采样。
对于一个样本,它在某一次含m个样本的训练集的随机采样中,每次被采集到的概率是1/m。不被采集到的概率为1−1/m。如果m次采样都没有被采集中的概率是(1−1/m)m。当m→∞时,(1−1/m)m→ 1/e≃0.368。也就是说,在bagging每轮随机采样中,训练集中大约有**36.8%**的数据没有被采样集采集中。
对于这部分大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
4.2 随机森林
随机森林(Random Forests)是一种重要的基于Bagging的集成学习方法,可以用来做分类、回归等问题。它的组成是由多个弱学习器组成,CART(分类回归树)。
RF的生成过程是由一个到多个CART的生成构成。主要过程如下:
通过对训练数据样本以及属性进行抽样(针对某一个属性随机选择样本)
这里有两种情况:
1.有放回的采样:通过这种方式采样,有些样本可能是重复的,这样样本组成和原始数据集样本个数一样的数据集
2.不放回的采样:抽取大约60%训练信息来生成一颗CART树,剩下的样本信息当作验证集用来计算袋外误差测试模型
把抽取出的样本信息再放回到原数据集中,再重新抽取一组训练信息,再以此训练数据集生成一颗CART树。重复上述方法生成多棵CART树组成森林,因为他们的生成都是通过随机采样的方式,因此叫作随机森林。
RF可以用于数据的回归,也可以用于数据的分类。回归时是由多颗树的预测结果求均值;分类是由多棵树的预测结果进行投票。
正因为它的随机性,RF可以很好地防止过拟合,且由于它是由CART组成,其训练数据不需要归一化,因为每棵树的建立过程都是通过选择一个能最好的对数据样本进行选择的属性来建立分叉,这也带来了一个缺点:忽略了属性间的关系。
分类:如果cart树是分类数,那么采用的计算原则就是gini指数。
基尼指数
定义:基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
即 基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
ps:
1.pk表示选中的样本属于k类别的概率,则这个样本被分错的概率是(1-pk)
2.样本集合中有K个类别,一个随机选中的样本可以属于这k个类别中的任意一个,因而对类别就加和。
对于二分类:Gini§ = 2p(1-p)
样本集合D的Gini指数 :假设集合中有K个类别,则:
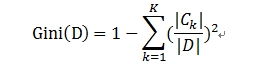
回归:
如果cart树是回归树,采用的原则是最小均方差。
即对于任意划分特征(属性)A,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为:

其中,c1为D1数据集的样本输出均值,c2为D2数据集的样本输出均值。 cart树的预测是根据叶子结点的均值,因此随机森林的预测是所有树的预测值的平均值。
参考链接1https://blog.csdn.net/ch0831/article/details/80387930
参考链接2https://www.jianshu.com/p/f219ba7f44b5