利用matlab绘制二维均匀流线和向量场
利用matlab绘制二维均匀流线和向量场(向量场彩色箭头,颜色随变量变化)
- 0前言
- 1 均匀流线的绘制
- 2 绘制彩色的短线图
- 3 绘制彩色的均匀流线
- 4 运动的彩色箭头流线图
0前言
之前一篇文章matlab流场可视化后处理我简单介绍了很多绘制流场可视化的方法,但是在流线方面一直不是很满意,因为matlab自带的绘制流线函数streamslice没有开源,有些参数(比如每根流线的颜色)不能修改等,所以我尝试着自己写一种绘制二维均匀流线的程序,以便满足更多的需求。
其中,matlab官方file exchange里,也有一些大神的代码给出了很好的结果:
Evenly Spaced Streamlines

Streamcolor

StreakArrow

关于如何用matlab绘制均匀的流线,我采用的方法是下面这篇论文提到的算法:
Jobard B., Lefer W. (1997) Creating Evenly-Spaced Streamlines of Arbitrary Density. In: Lefer W., Grave M. (eds) Visualization in Scientific Computing ’97. Eurographics. Springer, Vienna
1 均匀流线的绘制
论文Creating Evenly-Spaced Streamlines of Arbitrary Density中提出的绘制流线的算法可以描述为:
先初始化一根流线,然后在这个流线周围逐渐的扩展新的流线。文章中定义了两个距离,一个是用于产生新流线种子点的距离dstart,一个是用于结束流线生成的距离dend。新的流线扩展方式为,在距离旧的流线为dstart的随机位置上,生成一个种子点,对该种子点进行新流线的生成(同时向头和尾段生成流线),当新流线两端的点距某个旧流线的距离小于dend时,停止生成流线,将该流线放入旧流线内保存。当任意位置都不能满足新流线的生成时,则认为所有流线都已经生成,结束计算。
用伪代码的形式可以表述为
1 随机绘制第一根流线,作为初始流线。把初始流线加入已生成的流线列表内。把初始流线记为当前流线。
2 令Finish=False,当Finish==False时,进行循环
3 选择一个种子点,该点距 当前流线 的距离为dstart,且距离其它 已生成的流线列表内 的流线距离大于dstart
4 如果能够找到一个符合条件的种子点,则生成新的流线。
5 新流线以种子点为开始,向前向后伸展。
当流线的前端新计算的流线点距离某条流线的距离小于dend,则停止前端流线的生成。后端同样。
6 将新流线保存到已生成的流线列表内。
7 如果不能找到符合条件的种子点,则替换 当前流线 ,重复4
8 如果 已生成的流线列表内 所有流线都经过步骤7尝试一遍,则说明计算结束。
令Finish==True, 停止2的循环。
由于在计算中,用到了大量的距离计算,比如生成新种子点时,需要不停的和其它所有流线计算距离,保证大于dstart,又比如在计算新流线时,新流线每次生成一个点,该点都需要和所有以有的流线进行距离计算,保证距离大于dend。
这种频繁的距离计算数量,在量级上为N^2,这导致当流线上点比较多或者流线比较多时,计算会非常缓慢。我们可以利用一些其它的方法减少这种运算,比如利用划分网格的方式,使得每次计算距离,只需要计算周围网格(比如2维的周围网格有8个)内所有点的距离,而无需计算全局所有点的距离。或者利用树形搜索算法,可以将计算量降到NlgN的量级上。
当然,这里我利用一种更简单的方法进行计算。利用划分网格的思想,将新种子点的生成位置限定在网格上。而且,假设如果两个点在同一个网格内,说明两个点距离小于d,如果不在同一网格内,两个点距离大于d。这种假设虽然对计算结果不精准,但是仍然是可接受的,而且不需要计算距离。
用伪代码的形式可以表述为
1 生成距离dstart的网格。生成距离dend的网格。网格内初始化为0
2 当start网格内所有区域都为1,则停止循环
3 寻找start网格区域为0的区域,随机选择一个区域作为生成种子点。
4 以种子点为起始点,向前向后绘制流线
5 查询新生成的流线点对应的end网格,记为当前网格。
6 如果当前网格和上一个点的当前网格是同一个,则认为当前网格没有移动,继续生成下一个流线点
7 如果当前网格移动,且当前end网格为1,则停止生成流线。
8 如果当前网格移动,且当前end网格为0,则将当前网格标记为1,继续生成下一个流线点
9 将流线保存。流线经过的所有start网格标记为1。流线经过的所有end网格标记为1。之后重复3。
matlab代码为:
clear
clc
close all
%载入数据
load wind
N=5; xx=x(:,:,N); yy=y(:,:,N); uu=u(:,:,N); vv=v(:,:,N);
%由于这里R2018b之前的版本会出现兼容性问题,所以更改
%xmin=min(x,[],'all');xmax=max(x,[],'all');
%ymin=min(y,[],'all');ymax=max(y,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
%流线求解
streamline_sum=my_streamline(xx,yy,uu,vv,0.05);
%绘制流线
figure(1)
hold on
xlim([xmin,xmax]);
ylim([ymin,ymax]);
xy_ratio = get(gca, 'DataAspectRatio');
xy_ratio = xy_ratio(1:2);
xy_lim = axis;
for j=1:size(streamline_sum,2)
if size(streamline_sum{j},1)<=1
continue%忽略异常流线
end
plot(streamline_sum{j}(:,1),streamline_sum{j}(:,2),'k');
%绘制箭头
arrow_direction=streamline_sum{j}(end,:)-streamline_sum{j}(end-1,:);
plot_arrow(xy_lim,xy_ratio,streamline_sum{j}(end,:),[0,0,0],0.8,arrow_direction)
end
hold off
function streamline_sum=my_streamline(x,y,u,v,dstart)
%0处理前设置
%设置网格密度(01区间内归一化的长度)
%dstart=0.05;默认0.05
dend=0.5*dstart;
%xmin=min(x,[],'all');xmax=max(x,[],'all');
%ymin=min(y,[],'all');ymax=max(y,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
%归一化,将流场缩放为0-1区间的矩形
xn=(x-xmin)/(xmax-xmin);
yn=(y-ymin)/(ymax-ymin);
un=u/(xmax-xmin);
vn=v/(ymax-ymin);
num_start=ceil((0.5-dstart/2)/dstart)*2+1;
num_end=ceil((0.5-dend/2)/dend)*2+1;
%初始化所有网格点,0代表可以放置新点,1代表已经存在原有的点
xy_start=zeros(num_start,num_start);
xy_end=zeros(num_end,num_end);
%1当xy_start内还有可放置的新点的位置时,进行循环
k=0;%循环次数,也是流线个数
while ~all(xy_start,'all')
k=k+1;
%2随机一个start内网格点作为种子点
[start_id_y,start_id_x]=find(xy_start==0);
randnum=randi(size(start_id_y,1));
x_pos_i=id2axis(dstart,start_id_x(randnum,1));
y_pos_i=id2axis(dstart,start_id_y(randnum,1));
%3绘制流线
streamline_i_1 = stream2(xn,yn, un, vn,x_pos_i,y_pos_i,0.2);
streamline_i_2 = stream2(xn,yn,-un,-vn,x_pos_i,y_pos_i,0.2);
%4以xy_end为标准,删除自相交或间隔太近的点。并顺便标记xy_end
[streamline_i_1,xy_end,xy_start]=delete_self(streamline_i_1{1},xy_end,dend,xy_start,dstart);
[streamline_i_2,xy_end,xy_start]=delete_self(streamline_i_2{1},xy_end,dend,xy_start,dstart);
%5保存
streamline_k=[flipud(streamline_i_2);streamline_i_1(2:end,:)];%新的流线
streamline_sum{k}=[xmin+streamline_k(:,1)*(xmax-xmin),ymin+streamline_k(:,2)*(ymax-ymin)];%从归一化还原
end
end
function xpoint=id2axis(distance,id)
%取网格的中点
N=ceil((0.5-distance/2)/distance)*2+1;%分割的数量
min_distance=(1-(N-2)*distance)/2;%两端最小的距离
if id==1
xpoint=min_distance/2;
elseif id==N
xpoint=1-min_distance/2;
else
xpoint=min_distance+(id-1.5)*distance;
end
end
function [sl_i,xy_end,xy_start]=delete_self(sl_i,xy_end,dend,xy_start,dstart)
%sl_i streamline流线,两列N行形式
N=size(sl_i,1);
pos_id_last=axis2id(sl_i(1,1),sl_i(1,2),dend);
xy_end(pos_id_last)=1;%第一个点标记
%顺便标记xy_start
pos_id_s=axis2id(sl_i(1,1),sl_i(1,2),dstart);
xy_start(pos_id_s)=1;
for j=2:N
pos_id_now=axis2id(sl_i(j,1),sl_i(j,2),dend);
if pos_id_now~=pos_id_last
%如果现在的点和原有的点在同一区域,则不管它
%如果不在同一区域,检测新的点是否已经被占用
if xy_end(pos_id_now)==1
%如果该点被占用,说明出现与其它流线太近的情况,则直接停止
j=j-1;
break
else
%如果没被占用,则把新点添加上
xy_end(pos_id_now)=1;
pos_id_last=pos_id_now;
end
end
%顺便标记xy_start
pos_id_s=axis2id(sl_i(j,1),sl_i(j,2),dstart);
xy_start(pos_id_s)=1;
end
sl_i(j:end,:)=[];
end
function pos_id=axis2id(x,y,distance)
N=ceil((0.5-distance/2)/distance)*2+1;%分割的数量
min_distance=(1-(N-2)*distance)/2;%两端最小的距离
%x的位置
if x<=min_distance
pos_id_x=1;
elseif x>=1-min_distance
pos_id_x=N;
else
pos_id_x=ceil((x-min_distance)/distance)+1;
end
%y的位置
if y<=min_distance
pos_id_y=1;
elseif y>=1-min_distance
pos_id_y=N;
else
pos_id_y=ceil((y-min_distance)/distance)+1;
end
%xy转ind
pos_id=sub2ind([N,N],pos_id_y,pos_id_x);
end
function plot_arrow(xy_lim,xy_ratio,xy_arrow,arrow_color,arrow_width,arrow_direction)
%初始化箭头形状(归一化的形状)
arrow_0=[0,0;-1,0.5;-1,-0.5];
%对方向进行归一化
a_dn=arrow_direction(:)./xy_ratio(:);
a_dn=a_dn/sqrt(sum(a_dn.^2));
d=(xy_lim(4)-xy_lim(3)+xy_lim(2)-xy_lim(1))/2;
%箭头对窗口缩放
arrow_1=arrow_0*arrow_width*0.03*d;
%箭头旋转
arrow_2=arrow_1*[a_dn(1),a_dn(2);-a_dn(2),a_dn(1)];
%箭头变形
xy_ratio_n=xy_ratio/sqrt(sum(xy_ratio.^2));%对比例尺归一化
arrow_3=arrow_2.*xy_ratio_n+xy_arrow;
fill(arrow_3(:,1),arrow_3(:,2),arrow_color,'EdgeColor','none')
end
2 绘制彩色的短线图
这个绘制思路很简单,就是取每一个点,然后绘制短流线即可。
代码如下:
clear
clc
close all
%绘制短线彩色图(长短相同)
%载入数据
load wind
N=5; xx=x(:,:,N); yy=y(:,:,N); uu=u(:,:,N); vv=v(:,:,N);
%xmin=min(xx,[],'all');xmax=max(xx,[],'all');
%ymin=min(yy,[],'all');ymax=max(yy,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
V2=sqrt(uu.^2+vv.^2);%计算速度
%绘制变量颜色条
N_color=32;
P=V2;%把速度作为变量
%P_max=max(P,[],'all');P_min=min(P,[],'all');
P_max=max(max(max(P)));P_min=min(min(min(P)));
Num=numel(xx);%流线数量
for k=1:Num
startx=xx(k);starty=yy(k);
sl_i=stream2(xx,yy,uu,vv,startx,starty,[0.1, 20]);
sl_sum{k}=sl_i{1};%保存流线
end
mcp=colormap(parula(N_color));%生成颜色
[~,~,P_color] = histcounts(P(:),linspace(P_min,P_max,N_color));%颜色索引
figure(1)
hold on
xlim([xmin,xmax])
ylim([ymin,ymax])
xy_ratio = get(gca, 'DataAspectRatio');
xy_ratio = xy_ratio(1:2);
xy_lim = axis;
for k=1:Num
plot(sl_sum{k}(:,1),sl_sum{k}(:,2),'color',mcp(P_color(k),:))
if size(sl_sum{k},1)<=1
continue
end
%绘制箭头
arrow_direction=sl_sum{k}(end,:)-sl_sum{k}(end-1,:);
plot_arrow(xy_lim,xy_ratio,sl_sum{k}(end,:),mcp(P_color(k),:),0.5,arrow_direction)
end
hold off
caxis([P_min,P_max])%颜色条范围
colorbar
function plot_arrow(xy_lim,xy_ratio,xy_arrow,arrow_color,arrow_width,arrow_direction)
%初始化箭头形状(归一化的形状)
arrow_0=[0,0;-1,0.5;-1,-0.5];
%对方向进行归一化
a_dn=arrow_direction(:)./xy_ratio(:);
a_dn=a_dn/sqrt(sum(a_dn.^2));
d=(xy_lim(4)-xy_lim(3)+xy_lim(2)-xy_lim(1))/2;
%箭头对窗口缩放
arrow_1=arrow_0*arrow_width*0.03*d;
%箭头旋转
arrow_2=arrow_1*[a_dn(1),a_dn(2);-a_dn(2),a_dn(1)];
%箭头变形
xy_ratio_n=xy_ratio/sqrt(sum(xy_ratio.^2));%对比例尺归一化
arrow_3=arrow_2.*xy_ratio_n+xy_arrow;
fill(arrow_3(:,1),arrow_3(:,2),arrow_color,'EdgeColor','none')
end
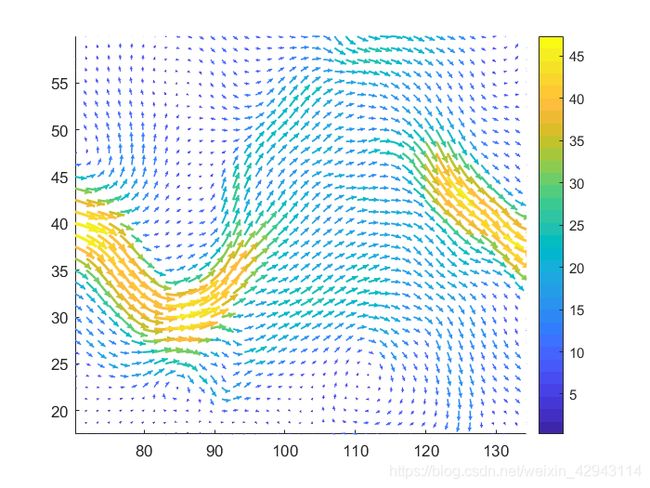
绘制出的效果如下:

这些流线基本都是长短相同的,因为stream2函数生成的流线,流线上的点基本是等间距的。如果想做出速度V大的流线箭头更长,速度小的流线更短的效果,这里用自己编写的二阶RK流线生成算法,进行流线的绘制。由于interp2速度太慢,这里用griddedInterpolant函数进行替换,优化速度将近10倍(我也没搞清楚为什么interp2速度这么慢)。
matlab代码如下:
clear
clc
close all
%绘制彩色短线图(长短不同)
%载入数据
load wind
N=5; xx=x(:,:,N); yy=y(:,:,N); uu=u(:,:,N); vv=v(:,:,N);
%xmin=min(xx,[],'all');xmax=max(xx,[],'all');
%ymin=min(yy,[],'all');ymax=max(yy,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
V2=sqrt(uu.^2+vv.^2);%计算速度
%绘制变量颜色条
N_color=32;
P=V2;%指定变量为V2
%P_max=max(P,[],'all');P_min=min(P,[],'all');
P_max=max(max(max(P)));P_min=min(min(min(P)));
Num = numel(xx);
num_streamline=20;%每条流线上的点数量
V2_max=max(max(max(V2)));
dt=3.0*min([xx(1,2)-xx(1,1),yy(2,1)-yy(1,1)])/V2_max/num_streamline;
for k=1:Num
startx=xx(k);starty=yy(k);
sl_i=stream2_RK2(xx,yy,uu,vv,startx,starty,dt,num_streamline);
sl_sum{k}=sl_i;
end
mcp=colormap(parula(N_color));
[~,~,P_color] = histcounts(P(:),linspace(P_min,P_max,N_color));
mlw=linspace(0.5,2,N_color);
figure(1)
hold on
xlim([xmin,xmax])
ylim([ymin,ymax])
xy_ratio = get(gca, 'DataAspectRatio');
xy_ratio = xy_ratio(1:2);
xy_lim = axis;
for k=1:Num
plot(sl_sum{k}(:,1),sl_sum{k}(:,2),'color',mcp(P_color(k),:),'linewidth',mlw(P_color(k)))
if size(sl_sum{k},1)<=1
continue
end
%绘制箭头
arrow_direction=sl_sum{k}(end,:)-sl_sum{k}(end-1,:);
plot_arrow(xy_lim,xy_ratio,sl_sum{k}(end,:),mcp(P_color(k),:),0.5*mlw(P_color(k)),arrow_direction)
end
hold off
caxis([P_min,P_max])
colorbar
function streamline_i=stream2_RK2(x,y,u,v,startx,starty,dt,N)
streamline_i=zeros(N,2);
streamline_i(1,:)=[startx,starty];
x_old=startx;y_old=starty;
F_u = griddedInterpolant(x',y',u','linear');
F_v = griddedInterpolant(x',y',v','linear');
for k=2:N
%利用改进欧拉法(或者叫2阶Runge-Kutta,预估校正)
%interp2太慢,放弃
% u_K1=interp2(x,y,u,x_old,y_old,'linear')*dt;
% v_K1=interp2(x,y,v,x_old,y_old,'linear')*dt;
u_K1 = F_u(x_old,y_old)*dt;
v_K1 = F_v(x_old,y_old)*dt;
% u_K2=interp2(x,y,u,x_old+0.5*u_K1,y_old+0.5*v_K1,'linear')*dt;
% v_K2=interp2(x,y,v,x_old+0.5*u_K1,y_old+0.5*v_K1,'linear')*dt;
u_K2 = F_u(x_old+0.5*u_K1,y_old+0.5*v_K1)*dt;
v_K2 = F_v(x_old+0.5*u_K1,y_old+0.5*v_K1)*dt;
x_new=x_old+0.5*(u_K1+u_K2);
y_new=y_old+0.5*(v_K1+v_K2);
%保存
streamline_i(k,:)=[x_new,y_new];
x_old=x_new;y_old=y_new;
if isnan(x_new) || isnan(y_new)
streamline_i(k+1:end,:)=[];
break
end
end
end
function plot_arrow(xy_lim,xy_ratio,xy_arrow,arrow_color,arrow_width,arrow_direction)
%初始化箭头形状(归一化的形状)
arrow_0=[0,0;-1,0.5;-1,-0.5];
%对方向进行归一化
a_dn=arrow_direction(:)./xy_ratio(:);
a_dn=a_dn/sqrt(sum(a_dn.^2));
d=(xy_lim(4)-xy_lim(3)+xy_lim(2)-xy_lim(1))/2;
%箭头对窗口缩放
arrow_1=arrow_0*arrow_width*0.03*d;
%箭头旋转
arrow_2=arrow_1*[a_dn(1),a_dn(2);-a_dn(2),a_dn(1)];
%箭头变形
xy_ratio_n=xy_ratio/sqrt(sum(xy_ratio.^2));%对比例尺归一化
arrow_3=arrow_2.*xy_ratio_n+xy_arrow;
fill(arrow_3(:,1),arrow_3(:,2),arrow_color,'EdgeColor','none')
end
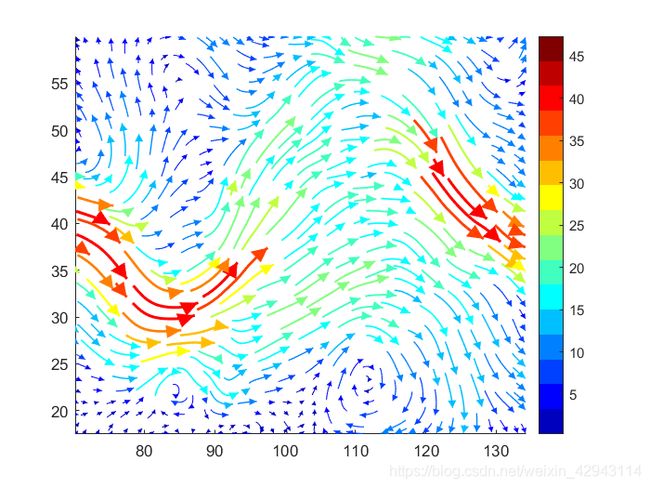
3 绘制彩色的均匀流线
流线的绘制采用第1小节方法,但是采用控制stream2函数的点数来控制流线的长度(没有采用第2小节的RK方法)。颜色的绘制采用第2小节的方法。
代码如下:
clear
clc
close all
%绘制彩色长线图(长短不同)
%载入数据
load wind
N=5; xx=x(:,:,N); yy=y(:,:,N); uu=u(:,:,N); vv=v(:,:,N);
%xmin=min(xx,[],'all');xmax=max(xx,[],'all');
%ymin=min(yy,[],'all');ymax=max(yy,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
%流线求解
[streamline_sum,streamline_seed]=my_streamline_mutli(xx,yy,uu,vv,0.03,32);
%绘制变量颜色条
V2=sqrt(uu.^2+vv.^2);
N_color=16;%流线的颜色种类
P=V2;%把速度作为颜色的变量
%P_max=max(P,[],'all');P_min=min(P,[],'all');
P_max=max(max(max(P)));P_min=min(min(min(P)));
mcp=colormap(jet(N_color));
P_seed=interp2(xx,yy,P,streamline_seed(:,1),streamline_seed(:,2));
[~,~,P_color] = histcounts(P_seed(:),linspace(P_min,P_max,N_color));
mlw=linspace(0.5,2,N_color);
%绘制流线
figure(1)
hold on
for j=1:size(streamline_sum,2)
plot(streamline_sum{j}(:,1),streamline_sum{j}(:,2),'color',mcp(P_color(j),:)...
,'linewidth',mlw(P_color(j)));%绘制流线
end
xlim([xmin,xmax])
ylim([ymin,ymax])
caxis([P_min,P_max])
colorbar
%绘制箭头
xy_ratio = get(gca, 'DataAspectRatio');
xy_ratio = xy_ratio(1:2);
xy_lim = axis;
for k=1:size(streamline_sum,2)
%绘制箭头
arrow_direction=streamline_sum{k}(end,:)-streamline_sum{k}(end-1,:);
plot_arrow(xy_lim,xy_ratio,streamline_sum{k}(end,:),mcp(P_color(k),:),mlw(P_color(k)),arrow_direction)
end
hold off
function [streamline_sum,streamline_seed]=my_streamline_mutli(x,y,u,v,dstart,num)
%0处理前设置
%设置网格密度(01区间内归一化的长度)
%dstart=0.05;默认0.05
dend=0.5*dstart;
%xmin=min(x,[],'all');xmax=max(x,[],'all');
%ymin=min(y,[],'all');ymax=max(y,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
%归一化,将流场缩放为0-1区间的矩形
xn=(x-xmin)/(xmax-xmin);
yn=(y-ymin)/(ymax-ymin);
un=u/(xmax-xmin);
vn=v/(ymax-ymin);
num_start=ceil((0.5-dstart/2)/dstart)*2+1;
num_end=ceil((0.5-dend/2)/dend)*2+1;
%初始化所有网格点,0代表可以放置新点,1代表已经存在原有的点
xy_start=zeros(num_start,num_start);
xy_end=zeros(num_end,num_end);
%将流线划分为num种,速度越大的流线越长
length_sl=linspace(5,40,num);
V2=sqrt(un.^2+vn.^2);
V2_max=max(max(max(V2)));
V2_min=min(min(min(V2)));
%V2_min=min(V2,[],'all');V2_max=max(V2,[],'all');
V2_space=linspace(V2_min,V2_max,num+1);
%1当xy_start内还有可放置的新点的位置时,进行循环
k=0;%循环次数,也是流线个数
while ~all(xy_start,'all')
k=k+1;
%2随机一个start内网格点作为种子点
[start_id_y,start_id_x]=find(xy_start==0);
randnum=randi(size(start_id_y,1));
x_pos_i=id2axis(dstart,start_id_x(randnum,1));
y_pos_i=id2axis(dstart,start_id_y(randnum,1));
streamline_seed(k,:)=[x_pos_i,y_pos_i];%保存种子点
V2_seed=interp2(xn,yn,V2,x_pos_i,y_pos_i);%计算种子点处的速度
[~,~,sl_N] = histcounts(V2_seed,V2_space);
num_streamline=round(length_sl(sl_N));
%3绘制流线
streamline_i_1 = stream2(xn,yn, un, vn,x_pos_i,y_pos_i,[0.1,num_streamline]);
streamline_i_2 = stream2(xn,yn,-un,-vn,x_pos_i,y_pos_i,[0.1,num_streamline]);
%4以xy_end为标准,删除自相交或间隔太近的点。并顺便标记xy_end
[streamline_i_1,xy_end,xy_start]=delete_self(streamline_i_1{1},xy_end,dend,xy_start,dstart);
[streamline_i_2,xy_end,xy_start]=delete_self(streamline_i_2{1},xy_end,dend,xy_start,dstart);
%5保存
streamline_k=[flipud(streamline_i_2);streamline_i_1(2:end,:)];%新的流线
streamline_sum{k}=[xmin+streamline_k(:,1)*(xmax-xmin),ymin+streamline_k(:,2)*(ymax-ymin)];%从归一化还原
end
streamline_seed=[streamline_seed(:,1)*(xmax-xmin)+xmin,streamline_seed(:,2)*(ymax-ymin)+ymin];
end
function xpoint=id2axis(distance,id)
%取网格的中点
N=ceil((0.5-distance/2)/distance)*2+1;%分割的数量
min_distance=(1-(N-2)*distance)/2;%两端最小的距离
if id==1
xpoint=min_distance/2;
elseif id==N
xpoint=1-min_distance/2;
else
xpoint=min_distance+(id-1.5)*distance;
end
end
function [sl_i,xy_end,xy_start]=delete_self(sl_i,xy_end,dend,xy_start,dstart)
%sl_i streamline流线,两列N行形式
N=size(sl_i,1);
pos_id_last=axis2id(sl_i(1,1),sl_i(1,2),dend);
xy_end(pos_id_last)=1;%第一个点标记
%顺便标记xy_start
pos_id_s=axis2id(sl_i(1,1),sl_i(1,2),dstart);
xy_start(pos_id_s)=1;
for j=2:N
pos_id_now=axis2id(sl_i(j,1),sl_i(j,2),dend);
if pos_id_now~=pos_id_last
%如果现在的点和原有的点在同一区域,则不管它
%如果不在同一区域,检测新的点是否已经被占用
if xy_end(pos_id_now)==1
%如果该点被占用,说明出现与其它流线太近的情况,则直接停止
j=j-1;
break
else
%如果没被占用,则把新点添加上
xy_end(pos_id_now)=1;
pos_id_last=pos_id_now;
end
end
%顺便标记xy_start
pos_id_s=axis2id(sl_i(j,1),sl_i(j,2),dstart);
xy_start(pos_id_s)=1;
end
sl_i(j:end,:)=[];
end
function pos_id=axis2id(x,y,distance)
N=ceil((0.5-distance/2)/distance)*2+1;%分割的数量
min_distance=(1-(N-2)*distance)/2;%两端最小的距离
%x的位置
if x<=min_distance
pos_id_x=1;
elseif x>=1-min_distance
pos_id_x=N;
else
pos_id_x=ceil((x-min_distance)/distance)+1;
end
%y的位置
if y<=min_distance
pos_id_y=1;
elseif y>=1-min_distance
pos_id_y=N;
else
pos_id_y=ceil((y-min_distance)/distance)+1;
end
%xy转ind
pos_id=sub2ind([N,N],pos_id_y,pos_id_x);
end
function plot_arrow(xy_lim,xy_ratio,xy_arrow,arrow_color,arrow_width,arrow_direction)
%初始化箭头形状(归一化的形状)
arrow_0=[0,0;-1,0.5;-1,-0.5];
%对方向进行归一化
a_dn=arrow_direction(:)./xy_ratio(:);
a_dn=a_dn/sqrt(sum(a_dn.^2));
d=(xy_lim(4)-xy_lim(3)+xy_lim(2)-xy_lim(1))/2;
%箭头对窗口缩放
arrow_1=arrow_0*arrow_width*0.03*d;
%箭头旋转
arrow_2=arrow_1*[a_dn(1),a_dn(2);-a_dn(2),a_dn(1)];
%箭头变形
xy_ratio_n=xy_ratio/sqrt(sum(xy_ratio.^2));%对比例尺归一化
%arrow_3=arrow_2.*xy_ratio_n+xy_arrow;%由于兼容性问题,更改为下面语句
xy_ratio_n2=ones(3,1)*xy_ratio_n;
arrow_3=arrow_2.*xy_ratio_n2+xy_arrow;
fill(arrow_3(:,1),arrow_3(:,2),arrow_color,'EdgeColor','none')
end
4 运动的彩色箭头流线图
一开始我本来是打算用第2小节的方式绘制一个动图,但是发现原来的箭头(粒子)离开之后,没有新的箭头进行补充。如果明确流场的入口和出口,可以采用出口离开多少粒子,就在入口添加多少粒子的方式,维持流场内数量恒定。但是对于复杂流场则不容易做到这点。
因此,我采用了均匀流线的方式,每次运动完成后,删除离得太近的流线,然后在空白处补充新的流线。效果如下:
这样做的优点在于每一帧都满足均匀流线的要求,而且保证绝大多数流线不会凭空的产生和消失,即使是消失也是逐渐消失。
代码如下:
clear
clc
close all
%绘制彩色长线图(长短不同,而且是会动的那种gif图)
%载入数据
load wind
N=5; xx=x(:,:,N); yy=y(:,:,N); uu=u(:,:,N); vv=v(:,:,N);
%xmin=min(xx,[],'all');xmax=max(xx,[],'all');
%ymin=min(yy,[],'all');ymax=max(yy,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
dstart=0.03;%网格宽度
%流线求解
[streamline_sum,streamline_seed]=my_streamline_mutli(xx,yy,uu,vv,dstart,32);
%绘制变量颜色条
V2=sqrt(uu.^2+vv.^2);
N_color=16;%流线的颜色种类
P=V2;%把速度作为颜色的变量
%P_max=max(P,[],'all');P_min=min(P,[],'all');
P_max=max(max(max(P)));P_min=min(min(min(P)));
mcp=colormap(jet(N_color));
P_seed=interp2(xx,yy,P,streamline_seed(:,1),streamline_seed(:,2));
[~,~,P_color] = histcounts(P_seed(:),linspace(P_min,P_max,N_color));
mlw=linspace(0.5,2,N_color);
%绘制流线
figure(1)
hold on
for j=1:size(streamline_sum,2)
plot(streamline_sum{j}(:,1),streamline_sum{j}(:,2),'color',mcp(P_color(j),:)...
,'linewidth',mlw(P_color(j)));%绘制流线
end
xlim([xmin,xmax])
ylim([ymin,ymax])%固定图窗大小
caxis([P_min,P_max])%设定颜色条范围
colorbar%显示色条
xy_ratio = get(gca, 'DataAspectRatio');
xy_ratio = xy_ratio(1:2);
xy_lim = axis;
for k=1:size(streamline_sum,2)
%绘制箭头
if size(streamline_sum{k},1)<=2
continue
end
arrow_direction=streamline_sum{k}(end,:)-streamline_sum{k}(end-1,:);
plot_arrow(xy_lim,xy_ratio,streamline_sum{k}(end,:),mcp(P_color(k),:),mlw(P_color(k)),arrow_direction)
end
hold off
%保存gif图
frame=getframe(gca);
im=frame2im(frame);
[I,map]=rgb2ind(im,36);
imwrite(I,map,'temp.gif','gif', 'Loopcount',inf,'DelayTime',0.08);%第一张
%后续的变化
for k=1:60
%延长dt秒之后的图像
streamline_sum=my_streamline_time(xx,yy,uu,vv,streamline_sum,dstart,0.05);
figure(1)
clf
hold on
for j=1:size(streamline_sum,2)
sl_i=streamline_sum{j};
if isempty(sl_i)
continue
end
L_sl_i=size(sl_i,1);
P_sl=interp2(xx,yy,P,sl_i(round(L_sl_i/2),1),sl_i(round(L_sl_i/2),2));
[~,~,P_color] = histcounts(P_sl,linspace(P_min,P_max,N_color));
P_color(P_color==0)=1;
plot(sl_i(:,1),sl_i(:,2),'color',mcp(P_color,:)...
,'linewidth',mlw(P_color));%绘制流线
%绘制箭头
if size(sl_i,1)<=2
continue
end
arrow_direction=sl_i(end,:)-sl_i(end-1,:);
plot_arrow(xy_lim,xy_ratio,sl_i(end,:),mcp(P_color,:),mlw(P_color),arrow_direction)
end
hold off
xlim([xmin,xmax])
ylim([ymin,ymax])%固定图窗大小
caxis([P_min,P_max])%设定颜色条范围
colorbar%显示色条
pause(0.5)
%保存gif图
frame=getframe(gca);
im=frame2im(frame);
[I,map]=rgb2ind(im,36);
imwrite(I,map,'temp.gif','gif','WriteMode','append','DelayTime',0.08);
end
function [streamline_sum,streamline_seed]=my_streamline_mutli(x,y,u,v,dstart,num)
%绘制流线
%0处理前设置
%设置网格密度(01区间内归一化的长度)
%dstart=0.05;默认0.05
dend=0.5*dstart;
%xmin=min(x,[],'all');xmax=max(x,[],'all');
%ymin=min(y,[],'all');ymax=max(y,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
%归一化,将流场缩放为0-1区间的矩形
xn=(x-xmin)/(xmax-xmin);
yn=(y-ymin)/(ymax-ymin);
un=u/(xmax-xmin);
vn=v/(ymax-ymin);
F_u = griddedInterpolant(xn',yn',un','linear');
F_v = griddedInterpolant(xn',yn',vn','linear');
F_u_n = griddedInterpolant(xn',yn',-un','linear');
F_v_n = griddedInterpolant(xn',yn',-vn','linear');
num_start=ceil((0.5-dstart/2)/dstart)*2+1;
num_end=ceil((0.5-dend/2)/dend)*2+1;
%初始化所有网格点,0代表可以放置新点,1代表已经存在原有的点
xy_start=zeros(num_start,num_start);
xy_end=zeros(num_end,num_end);
%将流线划分为num种,速度越大的流线越长
length_sl=linspace(5,40,num);
V2=sqrt(un.^2+vn.^2);
%V2_min=min(V2,[],'all');V2_max=max(V2,[],'all');
V2_max=max(max(max(V2)));
V2_min=min(min(min(V2)));
V2_space=linspace(V2_min,V2_max,num+1);
%1当xy_start内还有可放置的新点的位置时,进行循环
k=0;%循环次数,也是流线个数
while ~all(xy_start,'all')
k=k+1;
%2随机一个start内网格点作为种子点
[start_id_y,start_id_x]=find(xy_start==0);
randnum=randi(size(start_id_y,1));
x_pos_i=id2axis(dstart,start_id_x(randnum,1));
y_pos_i=id2axis(dstart,start_id_y(randnum,1));
streamline_seed(k,:)=[x_pos_i,y_pos_i];%保存种子点
%3绘制流线
streamline_i_1=stream2_RK2(F_u ,F_v ,x_pos_i,y_pos_i,0.01,20);
streamline_i_2=stream2_RK2(F_u_n,F_v_n,x_pos_i,y_pos_i,0.01,20);
%4以xy_end为标准,删除自相交或间隔太近的点。并顺便标记xy_end
[streamline_i_1,xy_end,xy_start]=delete_self(streamline_i_1,xy_end,dend,xy_start,dstart);
[streamline_i_2,xy_end,xy_start]=delete_self(streamline_i_2,xy_end,dend,xy_start,dstart);
%5保存
streamline_k=[flipud(streamline_i_2);streamline_i_1(2:end,:)];%新的流线
streamline_sum{k}=[xmin+streamline_k(:,1)*(xmax-xmin),ymin+streamline_k(:,2)*(ymax-ymin)];%从归一化还原
end
streamline_seed=[streamline_seed(:,1)*(xmax-xmin)+xmin,streamline_seed(:,2)*(ymax-ymin)+ymin];
end
function xpoint=id2axis(distance,id)
%取网格的中点
N=ceil((0.5-distance/2)/distance)*2+1;%分割的数量
min_distance=(1-(N-2)*distance)/2;%两端最小的距离
if id==1
xpoint=min_distance/2;
elseif id==N
xpoint=1-min_distance/2;
else
xpoint=min_distance+(id-1.5)*distance;
end
end
function [sl_i,xy_end,xy_start]=delete_self(sl_i,xy_end,dend,xy_start,dstart)
%sl_i streamline流线,两列N行形式
N=size(sl_i,1);
pos_id_last=axis2id(sl_i(1,1),sl_i(1,2),dend);
xy_end(pos_id_last)=1;%第一个点标记
%顺便标记xy_start
pos_id_s=axis2id(sl_i(1,1),sl_i(1,2),dstart);
xy_start(pos_id_s)=1;
for j=2:N
pos_id_now=axis2id(sl_i(j,1),sl_i(j,2),dend);
if pos_id_now~=pos_id_last
%如果现在的点和原有的点在同一区域,则不管它
%如果不在同一区域,检测新的点是否已经被占用
if xy_end(pos_id_now)==1
%如果该点被占用,说明出现与其它流线太近的情况,则直接停止
j=j-1;
break
else
%如果没被占用,则把新点添加上
xy_end(pos_id_now)=1;
pos_id_last=pos_id_now;
end
end
%顺便标记xy_start
pos_id_s=axis2id(sl_i(j,1),sl_i(j,2),dstart);
xy_start(pos_id_s)=1;
end
sl_i(j:end,:)=[];%删除停止之后剩余的流线
end
function pos_id=axis2id(x,y,distance)
N=ceil((0.5-distance/2)/distance)*2+1;%分割的数量
min_distance=(1-(N-2)*distance)/2;%两端最小的距离
%x的位置
if x<=min_distance
pos_id_x=1;
elseif x>=1-min_distance
pos_id_x=N;
else
pos_id_x=ceil((x-min_distance)/distance)+1;
end
%y的位置
if y<=min_distance
pos_id_y=1;
elseif y>=1-min_distance
pos_id_y=N;
else
pos_id_y=ceil((y-min_distance)/distance)+1;
end
%xy转ind
pos_id=sub2ind([N,N],pos_id_y,pos_id_x);
end
function plot_arrow(xy_lim,xy_ratio,xy_arrow,arrow_color,arrow_width,arrow_direction)
%初始化箭头形状(归一化的形状)
arrow_0=[0,0;-1,0.5;-1,-0.5];
%对方向进行归一化
a_dn=arrow_direction(:)./xy_ratio(:);
a_dn=a_dn/sqrt(sum(a_dn.^2));
d=(xy_lim(4)-xy_lim(3)+xy_lim(2)-xy_lim(1))/2;
%箭头对窗口缩放
arrow_1=arrow_0*arrow_width*0.03*d;
%箭头旋转
arrow_2=arrow_1*[a_dn(1),a_dn(2);-a_dn(2),a_dn(1)];
%箭头变形
xy_ratio_n=xy_ratio/sqrt(sum(xy_ratio.^2));%对比例尺归一化
%arrow_3=arrow_2.*xy_ratio_n+xy_arrow;%由于兼容性问题,更改为下面语句
xy_ratio_n2=ones(3,1)*xy_ratio_n;
arrow_3=arrow_2.*xy_ratio_n2+xy_arrow;
fill(arrow_3(:,1),arrow_3(:,2),arrow_color,'EdgeColor','none')
end
function streamline_i=stream2_RK2(F_u,F_v,startx,starty,dt,N)
%绘制流线,采用RK方法
%利用改进欧拉法(或者叫2阶Runge-Kutta,预估校正)
streamline_i=zeros(N,2);
streamline_i(1,:)=[startx,starty];
x_old=startx;y_old=starty;
for k=2:N
u_K1 = F_u(x_old,y_old)*dt;
v_K1 = F_v(x_old,y_old)*dt;
u_K2 = F_u(x_old+0.5*u_K1,y_old+0.5*v_K1)*dt;
v_K2 = F_v(x_old+0.5*u_K1,y_old+0.5*v_K1)*dt;
x_new=x_old+0.5*(u_K1+u_K2);
y_new=y_old+0.5*(v_K1+v_K2);
%保存
streamline_i(k,:)=[x_new,y_new];
x_old=x_new;y_old=y_new;
if isnan(x_new) || isnan(y_new)
streamline_i(k+1:end,:)=[];
break
end
if 0>x_new || 0>y_new || x_new>1 || y_new>1
%由于插值结果都是在0-1区间内的归一化数据,所以超出边界的删除。
streamline_i(k+1:end,:)=[];
break
end
end
end
function streamline_sum=my_streamline_time(x,y,u,v,streamline_sum,dstart,dt)
%0处理前设置
%xmin=min(x,[],'all');xmax=max(x,[],'all');
%ymin=min(y,[],'all');ymax=max(y,[],'all');
xmin=min(min(min(x)));xmax=max(max(max(x)));
ymin=min(min(min(y)));ymax=max(max(max(y)));
%归一化,将流场缩放为0-1区间的矩形
xn=(x-xmin)/(xmax-xmin);
yn=(y-ymin)/(ymax-ymin);
un=u/(xmax-xmin);
vn=v/(ymax-ymin);
streamline_sum(cellfun(@isempty,streamline_sum))=[];%删除空数组
%排序,优先保证长线段不被删除
L_sl=zeros(length(streamline_sum),1);
for k=1:length(streamline_sum)
L_sl(k)=sum((streamline_sum{k}(end,:)-streamline_sum{k}(1,:)).^2);
end
[~,I]=sort(L_sl,'descend' );
streamline_sum(:,[1:length(streamline_sum)])=streamline_sum(:,[I]);
%设置网格密度(01区间内归一化的长度)
%dstart=0.05;默认0.05
dend=0.5*dstart;
%每一条流线随时间的变化
F_u = griddedInterpolant(xn',yn',un','linear');
F_v = griddedInterpolant(xn',yn',vn','linear');
F_u_n = griddedInterpolant(xn',yn',-un','linear');
F_v_n = griddedInterpolant(xn',yn',-vn','linear');
num_start=ceil((0.5-dstart/2)/dstart)*2+1;
num_end=ceil((0.5-dend/2)/dend)*2+1;
for k=1:length(streamline_sum)
sl_i=streamline_sum{k};
if isempty(sl_i)
continue
end
if any(isnan(sl_i(end,:)))
sl_i(1,:)=[];
else
sl_i(1,:)=[];
if isempty(sl_i)
continue
end
sl_i_n=(sl_i-[xmin,ymin])./[(xmax-xmin),(ymax-ymin)];%归一化流线
sl_i_now=stream2_RK2(F_u ,F_v ,sl_i_n(end,1),sl_i_n(end,2),dt,2);
sl_i_n=[sl_i_n;sl_i_now(2,:)];
sl_i=sl_i_n.*[(xmax-xmin),(ymax-ymin)]+[xmin,ymin];%反归一化
end
streamline_sum{k}=sl_i;
end
streamline_sum(cellfun(@isempty,streamline_sum))=[];%删除空数组
xy_start=zeros(num_start,num_start);
xy_end=zeros(num_end,num_end);
for k=1:length(streamline_sum)
sl_i=streamline_sum{k};
sl_i=flipud(sl_i);%删除尾部,保留头部
sl_i_n=(sl_i-[xmin,ymin])./[(xmax-xmin),(ymax-ymin)];%归一化流线
%以xy_end为标准,删除自相交或间隔太近的点。并顺便标记xy_end
[sl_i_n,xy_end,xy_start]=delete_self(sl_i_n,xy_end,dend,xy_start,dstart);
sl_i=sl_i_n.*[(xmax-xmin),(ymax-ymin)]+[xmin,ymin];%反归一化
sl_i=flipud(sl_i);
streamline_sum{k}=sl_i;
end
%之后还有一些区域太空,所以重新在那些区域生成流线
while ~all(xy_start,'all')
k=k+1;
%2随机一个start内网格点作为种子点
[start_id_y,start_id_x]=find(xy_start==0);
randnum=randi(size(start_id_y,1));
x_pos_i=id2axis(dstart,start_id_x(randnum,1));
y_pos_i=id2axis(dstart,start_id_y(randnum,1));
%3绘制流线
streamline_i_1=stream2_RK2(F_u ,F_v ,x_pos_i,y_pos_i,0.01,20);
streamline_i_2=stream2_RK2(F_u_n,F_v_n,x_pos_i,y_pos_i,0.01,20);
%4以xy_end为标准,删除自相交或间隔太近的点。并顺便标记xy_end
[streamline_i_1,xy_end,xy_start]=delete_self(streamline_i_1,xy_end,dend,xy_start,dstart);
[streamline_i_2,xy_end,xy_start]=delete_self(streamline_i_2,xy_end,dend,xy_start,dstart);
%5保存
sl_i_n=[flipud(streamline_i_2);streamline_i_1(2:end,:)];%新的流线
sl_i=sl_i_n.*[(xmax-xmin),(ymax-ymin)]+[xmin,ymin];%反归一化
streamline_sum{k}=sl_i;
end
end