递归算法学习——电话号码的字母组成,括号生成,组合
目录
一,电话号码的字母组合
1.题意
2.例子
3.题目接口
4.解题代码和思路
代码:
思路:
二,括号的生成
1.题意
2.例子
3.题目接口
四,解题代码和思路
1.先写代码:
2.思路
三,组合
1.题意
2.例子
3.题目接口
4.解题代码
一,电话号码的字母组合
1.题意
给定一个仅包含数字
2-9的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
2.例子
比如以上例子,2对应的字母组合是"abc",3对应的字母组合是"def"。所以,这里便有两组字母组合,这两组字母组合的互相的两两搭配便是我们要找的答案。
3.题目接口
class Solution {
public:
vector letterCombinations(string digits) {
}
}; 4.解题代码和思路
代码:
class Solution {
string arr[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};//字母映射
vectorret;//存结果的数组
string path;//整合结果
public:
vector letterCombinations(string digits) {
if(digits.size()==0)
{
return ret;
}
dfs(digits,0);
return ret;
}
void dfs(string& digits,int pos)
{
if(path.size()==digits.size())//当path的长度和digits的长度相等的时候便可以加入到结果中
{
ret.push_back(path);
return;
}
string ch = arr[digits[pos]-'0'];
for(int i = 0;i 思路:
要解决这道题,首先便要搞一个能够映射的数组arr。这个数组一共有十位,前两位是空的。后八位便以电话键的数字为下标,字母为内容一一映射:
string arr[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};然后便是两个全局变量的设计,全局变量的使用只是为了能够让函数传参更加方便罢了。
在这里最重要的还是dfs函数的设计。
1.首先是函数头:
因为两个全局变量的设计,让我们的dfs函数的传参变得比较简单,只需要传入两个参数,一个是digits,另一个是下标pos:
void dfs(string& digits,int pos)2.递归的结束条件:
递归的结束条件就是上面的例子中所说的那样,当整合结果的path的长度等于digits的长度时便可以将结果留到ret里。然后再返回到上一层。
if(path.size()==digits.size()) { ret.push_back(path); return; }3.函数体的设计
要想设计好函数体,首先便要知道这个函数应该如何运行才能得到我们想要的结果。以digits==“23”为例。2:abc,3:def。结果为:["ad","ae","af","bd","be","bf","cd","ce","cf"]
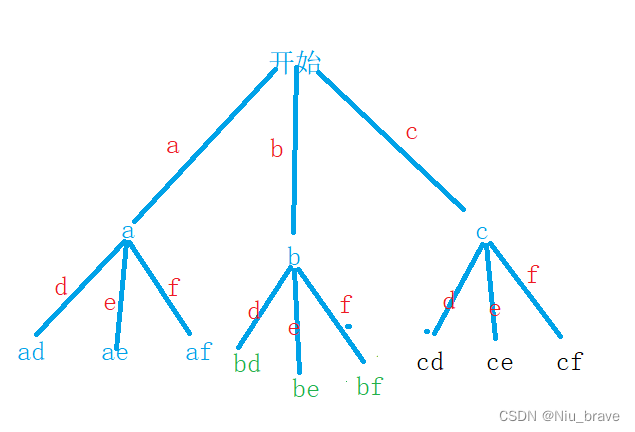
画出决策树:
从这个树形结构可以看出,在每一层要处理的节点的个数就是每一个string的个数。比如“abc”有三个字母组成,在这里便要处理3个节点。下一层的“def”也是。所以,处理每一层便可以使用for循环。于是得到下面的代码:
string ch = arr[digits[pos]-'0'];//得到每一层的string for(int i = 0;i层遍历加上深度优先遍历便构成这段代码的函数体。
二,括号的生成
1.题意
数字
n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
2.例子
以n=3为例子,那这个函数便要找出三个左括号:"("与三个右括号:")"的所有搭配。如上图所示。
3.题目接口
class Solution {
public:
vector generateParenthesis(int n) {
}
}; 四,解题代码和思路
1.先写代码:
class Solution {
vectorret;//存放最后的结果
string path;//记录每一个得到的结果
int right = 0;//记录有右括号的个数
int left = 0;//记录左括号的个数
public:
vector generateParenthesis(int n) {
dfs(n);
return ret;
}
void dfs(int& n)
{
if(path.size()==2*n)
{
ret.push_back(path);
return;
}
if(left 2.思路
先来讲一讲这道题的关键问题:括号的有效性。先以n==3为例子,这个时候左括号和右括号在什么时候插入到path中才是合法的呢?这就要从左右括号的插入顺序和数量来讨论了。
1.首先得是顺序:第一个插入的括号必须为左括号。这个该如何控制呢?实现这个逻辑的代码如下:
if(right只有在右括号的数量小于左括号时才能插入右括号,这也就保证了path第一个插入的括号是(。
2.括号的数量,因为右括号的数量在递归的过程中是一直小于或者等于left的。所以控制了左括号的数量小于n便是控制了有括号的数量小于n。所以代码如下:
if(left当n==2时,决策树:
三,组合
1.题意
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
2.例子
这道题对我们的要求便是要求出在1~n之间按k个数的组合。并且一个组合和另一个组合的数字不同才能叫做不同的组合。顺序不同不能叫做组合。
3.题目接口
class Solution {
public:
vector> combine(int n, int k) {
}
}; 4.解题代码
class Solution {
public:
vector>ret;
vectorpath;
vector> combine(int n, int k) {
dfs(n,k,1);
return ret;
}
void dfs(int& n,int& k,const int& pos)//用引用要加const,不加就是权限的放大。
{
if(path.size()==k)
{
ret.push_back(path);
return;
}
for(int i = pos;i<=n;i++)//用下标来控制剪枝
{
path.push_back(i);
dfs(n,k,i+1);
path.pop_back();
}
}
};