CF Round 479 (Div. 3)--E. Cyclic Components(DFS求无向图中独立环的个数)

You are given an undirected graph consisting of n vertices and m edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex a is connected with a vertex b, a vertex b is also connected with a vertex a). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices u and v belong to the same connected component if and only if there is at least one path along edges connecting u and v.

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

• the first vertex is connected with the second vertex by an edge,
• the second vertex is connected with the third vertex by an edge,
• ...
• the last vertex is connected with the first vertex by an edge,
• all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

 

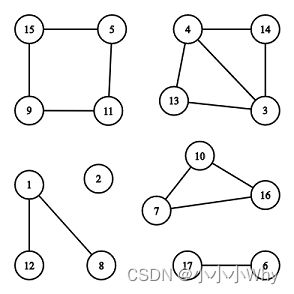
There are 6 connected components, 2 of them are cycles: [7,10,16] and [5,11,9,15].

Input

The first line contains two integer numbers n and m (1≤n≤2⋅10^5, 0≤m≤2⋅10^5) — number of vertices and edges.

The following m lines contains edges: edge i is given as a pair of vertices vi, ui (1≤vi,ui≤n, ui≠v). There is no multiple edges in the given graph, i.e. for each pair (vi,ui) there no other pairs (vi,ui) and (ui,vi) in the list of edges.

Output

Print one integer — the number of connected components which are also cycles.

input

5 4
1 2
3 4
5 4
3 5

output

1

题意：就是n个点，m条无向边，让你求出其中独立环的个数(环与环没有交集，且环没有其他无用边)。

解析：我们可以发现，对于一个合法环，环上每个点一定都连出去两条边，我们可以对于每一个没搜过的点，进行DFS，中间判断是否合法，如果到最后搜回来这个点，那么说明是一个环，如此计数即可。

#include 
using namespace std;
const int N=2e5+5;
vector v[N];
int cnt;
bool st[N],ok;
void dfs(int u,int fa)
{
    if(ok) return;//已经找到了
    if(st[u])
    {
        cnt++;//环的个数+1
        ok=true;
        return;
    }
    st[u]=true;
    for(int i=0;i