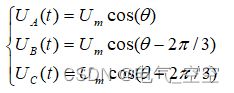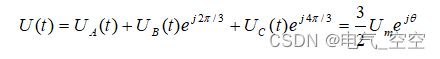SVPWM的原理及法则推导和控制算法详解

1. 空间电压矢量调制 SVPWM 技术

SVPWM是近年发展的一种比较新颖的控制方法，是由三相功率逆变器的六个功率开关元件组成的特定开关模式产生的脉宽调制波，能够使输出电流波形尽 可能接近于理想的正弦波形。空间电压矢量PWM与传统的正弦PWM不同，它是从三相输出电压的整体效果出发，着眼于如何使电机获得理想圆形磁链轨迹。 SVPWM技术与SPWM相比较，绕组电流波形的谐波成分小，使得电机转矩脉动降低，旋转磁场更逼近圆形，而且使直流母线电压的利用率有了很大提高，且更易于实现数字化。下面将对该算法进行详细分析阐述。

1. 1.  SVPWM基本原理

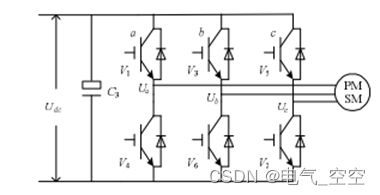
    SVPWM 的理论基础是平均值等效原理，即在一个开关周期内通过对基本电压矢量加以组合，使其平均值与给定电压矢量相等。在某个时刻，电压矢量旋转到某个区域中，可由组成这个区域的两个相邻的非零矢量和零矢量在时间上的不同组合来得到。两个矢量的作用时间在一个采样周期内分多次施加，从而控制各个电压矢量的作用时间，使电压空间矢量接近按圆轨迹旋转，通过逆变器的不同开关状态所产生的实际磁通去逼近理想磁通圆，并由两者的比较结果来决定逆变器的开关状态，从而形成PWM 波形。逆变电路如图 2-8 示。

设直流母线侧电压为Udc，逆变器输出的三相相电压为UA、UB、UC，其分别加在空间上互差120°的三相平面静止坐标系上，可以定义三个电压空间矢量 UA(t)、UB(t)、UC(t)，它们的方向始终在各相的轴线上，而大小则随时间按正弦规律做变化，时间相位互差120°。假设Um为相电压有效值，f为电源频率，则有：

                    （2-27）

其中，θ=2πft，，则三相电压空间矢量相加的合成空间矢量 U(t)就可以表示为：

    （2-28）   

可见 U(t)是一个旋转的空间矢量，它的幅值为相电压峰值的1.5倍，Um为相电压峰值，且以角频率ω=2πf按逆时针方向匀速旋转的空间矢量，而空间矢量 U(t)在三相坐标轴（a，b，c）上的投影就是对称的三相正弦量。

图 2-8  逆变电路

由于逆变器三相桥臂共有6个开关管，为了研究各相上下桥臂不同开关组合时逆变器输出的空间电压矢量，特定义开关函数 Sx ( x = a、b、c) 为：

（2-30）

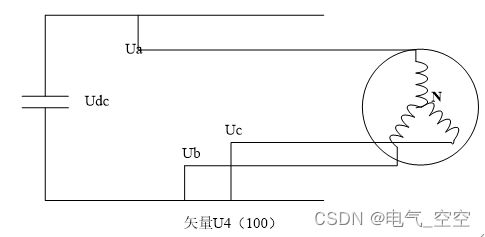
(Sa、Sb、Sc)的全部可能组合共有八个，包括6个非零矢量 Ul(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、和两个零矢量  U0(000)、U7(111)，下面以其中一 种开关 组 合为 例分 析，假设Sx ( x= a、b、c)= (100)， 此 时

                             

（2-30）

求解上述方程可得：Uan=2Ud /3、UbN=-U d/3、UcN=-Ud /3。同理可计算出其它各种组合下的空间电压矢量，列表如下：

表 2-1  开关状态与相电压和线电压的对应关系

Sa	Sb	Sc	矢量符号	线电压			相电压
				Uab	Ubc	Uca	UaN	UbN	UcN
0	0	0	U0	0	0	0	0	0	0
1	0	0	U4	Udc	0	0
1	1	0	U6	Udc	Udc	0
0	1	0	U2	0	Udc	Udc
0	1	1	U3	0	Udc	Udc
0	0	1	U1	0	0	Udc
1	0	1	U5	Udc	0	Udc
1	1	1	U7	0	0	0	0	0	0

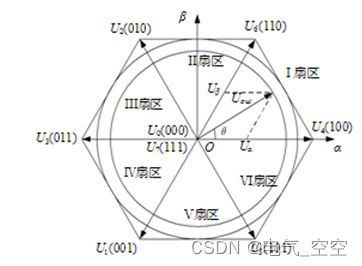
图 2-9 给出了八个基本电压空间矢量的大小和位置。

图 2-9 电压空间矢量图

    其中非零矢量的幅值相同（模长为 2Udc/3），相邻的矢量间隔 60°，而两个零矢量幅值为零，位于中心。在每一个扇区，选择相邻的两个电压矢量以及零矢量，按照伏秒平衡的原则来合成每个扇区内的任意电压矢量，即：

或者等效成下式：

（2-32）

    其中，Uref 为期望电压矢量；T为采样周期；Tx、Ty、T0分别为对应两个非零电压矢量 Ux、Uy 和零电压矢量 U 0在一个采样周期的作用时间；其中U0包括了U0和U7两个零矢量。式（2-32）的意义是，矢量 Uref 在 T 时间内所产生的积分效果值和 Ux、Uy、U 0 分别在时间 Tx、Ty、T0内产生的积分效果相加总和值相同。

    由于三相正弦波电压在电压空间向量中合成一个等效的旋转电压，其旋转速度是输入电源角频率，等效旋转电压的轨迹将是如图2-9 所示的圆形。所以要产生三相正弦波电压，可以利用以上电压向量合成的技术，在电压空间向量上，将设定的电压向量由U4(100)位置开始，每一次增加一个小增量，每一个小增量设定电压向量可以用该区中相邻的两个基本非零向量与零电压向量予以合成，如此所得到的设定电压向量就等效于一个在电压空间向量平面上平滑旋转的电压空间向量，从而达到电压空间向量脉宽调制的目的。

1. 1.  SVPWM 法则推导

三相电压给定所合成的电压向量旋转角速度为ω=2πf，旋转一周所需的时 间为 T =1/ f ；若载波频率是 fs ，则频率比为 R = f s / f  。这样将电压旋转平面等 切 割 成 R  个 小 增 量 ，亦 即 设 定 电 压 向 量 每 次 增 量 的 角 度 是 ：

   γ=2/ R =2πf/fs=2Ts/T。

今假设欲合成的电压向量Uref 在第Ⅰ区中第一个增量的位置，如图2-10所示，欲用 U4、U6、U0 及 U7 合成，用平均值等效可得：U ref*Tz =U 4*T4 +U 6*T6 。

图 2-10  电压空间向量在第Ⅰ区的合成与分解

在两相静止参考坐标系（α，β）中，令 Uref 和 U4 间的夹角是θ，由正弦定理

可得：

  

                                         （2-34）

式中 m 为 SVPWM 调制系数（调制比）， m=

|Uref|/Udc 。

而零电压向量所分配的时间为：

T7=T0=(TS-T4-T6 ) /2                                                 （2-35）

或者T7 =(TS-T4-T6 )                                               （2-36）

得到以 U4、U6、U7 及 U0 合成的 Uref 的时间后，接下来就是如何产生实际的脉宽调制波形。在SVPWM 调制方案中，零矢量的选择是最具灵活性的，适当选择零矢量，可最大限度地减少开关次数，尽可能避免在负载电流较大的时刻的开关动作，最大限度地减少开关损耗。

一个开关周期中空间矢量按分时方式发生作用，在时间上构成一个空间矢量的序列，空间矢量的序列组织方式有多种，按照空间矢量的对称性分类，可分为两相开关换流与三相开关换流。下面对常用的序列做分别介绍。

1. 1. 1.      7段式SVPWM

我们以减少开关次数为目标，将基本矢量作用顺序的分配原则选定为：在每次开关状态转换时，只改变其中一相的 开关状态。并且对零矢量在时间上进行了平均分配，以使产生的 PWM 对称，从而有效地降低 PWM 的谐波分量。当 U4(100)切换至 U0(000)时，只需改变 A 相上下一对切换开关，若由 U4(100)切换至 U7(111)则需改变 B、C 相上下两对切换开关，增加了一倍的切换损失。因此要改变电压向量 U4(100)、U2(010)、 U1(001)的大小，需配合零电压向量 U0(000)，而要改变 U6(110)、U3(011)、U5(100)， 需配合零电压向量 U7(111)。这样通过在不同区间内安排不同的开关切换顺序， 就可以获得对称的输出波形，其它各扇区的开关切换顺序如表 2-2 所示。

表 2-2 UREF 所在的位置和开关切换顺序对照序

UREF 所在的位置	开关切换顺序		三相波形图
Ⅰ区（0°≤θ≤60°）	…0-4-6-7-7-6-4-0…
Ⅱ区（60°≤θ≤120°）	…0-2-6-7-7-6-2-0…
Ⅲ区（120°≤θ≤180°）	…0-2-3-7-7-3-2-0…
Ⅳ区（180°≤θ≤240°）	…0-1-3-7-7-3-1-0…
Ⅴ区（240°≤θ≤300°）	…0-1-5-7-7-5-1-0…
Ⅵ区（300°≤θ≤360°）	…0-4-5-7-7-5-4-0…

以第Ⅰ扇区为例，其所产生的三相波调制波形在时间 TS 时段中如图所示，图中电压向量出现的先后顺序为 U0、U4、U6、U7、U6、U4、U0，各电压向量的三相波形则与表 2-2 中的开关表示符号相对应。再下一个 TS 时段，Uref 的角度增加一个γ，利用式（2-33）可以重新计算新的 T0、T4、T6 及 T7 值，得到新的 合成三相类似（3-4）所示的三相波形；这样每一个载波周期TS就会合成一个新的矢量，随着θ的逐渐增大，Uref 将依序进入第Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ区。在电 压向量旋转一周期后，就会产生 R 个合成矢量。

1. 1. 1. 5段式SVPWM

对7段而言，发波对称，谐波含量较小，但是每个开关周期有6次开关切换，为了进一步减少开关次数，采用每相开关在每个扇区状态维持不变的序列安排，使得每个开关周期只有3次开关切换，但是会增大谐波含量。具体序列安排见下表。

表 2-3 UREF 所在的位置和开关切换顺序对照序

UREF 所在的位置	开关切换顺序		三相波形图
Ⅰ区（0°≤θ≤60°）	…4-6-7-7-6-4…
Ⅱ区（60°≤θ≤120°）	…2-6-7-7-6-2…
Ⅲ区（120°≤θ≤180°）	…2-3-7-7-3-2…
Ⅳ区（180°≤θ≤240°）	…1-3-7-7-3-1…
Ⅴ区（240°≤θ≤300°）	…1-5-7-7-5-1…
Ⅵ区（300°≤θ≤360°）	…4-5-7-7-5-4…

1. 1. SVPWM 控制算法

通过以上 SVPWM 的法则推导分析可知要实现SVPWM信号的实时调制，首先需要知道参考电压矢量 Uref 所在的区间位置，然后利用所在扇区的相邻两电压矢量和适当的零矢量来合成参考电压矢量。图2-10是在静止坐标系（α，β）中描述的电压空间矢量图，电压矢量调制的控制指令是矢量控制系统给出的矢量信号 Uref，它以某一角频率ω在空间逆时针旋转，当旋转到矢量图的某个 60°扇区中时，系统计算该区间所需的基本电压空间矢量，并以此矢量所对应的状态去驱动功率开关元件动作。当控制矢量在空间旋转 360°后，逆变器就能输出一个周期的正弦波电压。

1. 1. 1. 合成矢量 Uref 所处扇区 N 的判断

    空间矢量调制的第一步是判断由 Uα 和 Uβ所决定的空间电压矢量所处的扇区。假定合成的电压矢量落在第 I 扇区，可知其等价条件如下：

0º

以上等价条件再结合矢量图几何关系分析，可以判断出合成电压矢量 Uref 落在第 X扇区的充分必要条件,得出下表：

扇区	落在此扇区的充要条件
I	Uα>0 ，Uβ>0 且Uβ/ Uα<
Ⅱ	Uα>0 ， 且Uβ/ |Uα|>
Ⅲ	Uα<0 ，Uβ>0 且-Uβ/ Uα<
Ⅳ	Uα<0 ，Uβ<0 且Uβ/ Uα<
Ⅴ	Uβ<0 且-Uβ/|Uα|>
Ⅵ	Uα>0 ，Uβ<0 且-Uβ/Uα<

    若进一步分析以上的条件，有可看出参考电压矢量Uref 所在的扇区完全由Uβ,

 Uα- Uβ,-

 Uα- Uβ 三式决定，因此令：

再定义，若U1>0 ，则 A=1，否则 A=0； 若U 2>0 ，则 B=1，否则 B=0；若U3>0 ，则 C=1，否则 C=0。可以看出 A，B，C 之间共有八种组合，但由判断扇区的公式可知 A，B，C 不会同时为 1 或同时为 0，所以实际的组合是六种，A，B，C 组合取不同的值对 应着不同的扇区，并且是一一对应的，因此完全可以由 A，B，C 的组合判断所在的扇区。为区别六种状态，令 N=4*C+2*B+A，则可以通过下表计算参考电压 矢量 Uref 所在的扇区。

表 2-3 P 值与扇区对应关系

N	3	1	5	4	6	2
扇区号	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ

采用上述方法，只需经过简单的加减及逻辑运算即可确定所在的扇区，对于提高系统的响应速度和进行仿真都是很有意义的。

1. 1. 1. 基本矢量作用时间计算与三相 PWM 波形的合成

    在传统 SVPWM 算法如 式（2-34）中用到了空间角度及三角函数，使得直接计算基本电压矢量作用时间 变得十分困难。实际上，只要充分利用 Uα 和 Uβ 就可以使计算大为简化。以 Uref 处在第Ⅰ扇区时进行分析，根据图 2-10 有：

   

经过整理后得出：

 

     

同理可求得Uref在其它扇区中各矢量的作用时间，结果如表2-4所示。由此可根据式2-36  中的U1 、U 2 、U3 判断合成矢量所在扇区，然后查表得出两非零矢量的作用时间，最后得出三相PWM波占空比，表2-4可以使SVPWM算法编程简易实现。

为了实现对算法对各种电压等级适应，一般会对电压进行标幺化处理，实际电压

，

为标幺值，在定点处理其中一般为Q12格式，即标幺值为1时，等于4096，假定电压基值为

，Unom为系统额定电压，一般为线电压，这里看出基值为相电压的峰值。

以DSP的PWM模块为例，假设开关频率为fs，DSP的时钟为fdsp，根据PWM的设置要是想开关频率为fs时，PWM周期计数器的值为NTpwm=fdsp/fs/2,则对时间转换为计数值进行如下推导：

其中

和

为实际值的标幺值，令发波系数，Ksvpwm=

同理可以得到

表 2-4 各扇区基本空间矢量的作用时间

扇区	时间
I			TN4=TNx TN6=TNy
Ⅱ			TN2=TNx TN6=TNy
Ⅲ			TN2=TNx TN3=TNy
Ⅳ			TN1=TNx TN3=TNy
Ⅴ			TN1=TNx TN5=TNy
Ⅵ			TN4=TNx TN5=TNy

由公式（2-38）可知，当两个零电压矢量作用时间为0时，一个PWM周期内非零电压矢量的作用时间最长，此时的合成空间电压矢量幅值最大，由图2-12可 知其幅值最大不会超过图中所示的正六边形边界。而当合成矢量落在该边界之外 时，将发生过调制，逆变器输出电压波形将发生失真。在SVPWM调制模式下， 逆变器能够输出的最大不失真圆形旋转电压矢量为图2-12所示虚线正六边形的 内切圆，其幅值为：

，即逆变器输出的不失真最大 正弦相电压幅值为

 ，而若采用三相SPWM调制，逆变器能输出的不失真最大正弦相电压幅值为 U dc  /2 。显然SVPWM  调制模式下对直流侧电压利用率

更高，它们的直流利用率 之比为

，即SVPWM法比SPWM法的直流电压利用率提高了15.47%。

图2-12 SVPWM模式下电压矢量幅值边界

如图当合成电压矢量端点落在正六边形与外接圆之间时，已发生过调制，输出电压将发生失真，必须采取过调制处理，这里采用一种比例缩小算法。定义每个扇区中先发生的矢量用为 TNx，后发生的矢量为 TNy。当 Tx+Ty≤TNPWM 时，矢量端点在正六边形之内，不发生过调制；当  TNx+TNy> TNPWM时，矢量端点超出正六边形，发生过调制。输出的波形会出现严重的失真，需采取以下措施：

设将电压矢量端点轨迹端点拉回至正六边形内切圆内时两非零矢量作用时间分别为 TNx'，TNy'，则有比例关系：

                                                 （2-39）

因此可用下式求得 TNx'，TNy'，TN0，TN7：  

                                            （2-40）

按照上述过程，就能得到每个扇区相邻两电压空间矢量和零电压矢量的作用时间。当U ref所在扇区和对应有效电压矢量的作用时间确定后，再根据PWM调制原理，计算出每一相对应比较器的值，其运算关系如下

在I扇区时如下图，

  （2-41）

同理可以推出5段时，在I扇区时如式，

     （2-42）

不同PWM比较方式，计数值会完全不同，两者会差180度

段数	以倒三角计数，对应计数器的值	以正三角计数，对应计数器的值
7
5

其他扇区以此类推，可以得到表2-5，式中 Ntaon 、Ntbon 和Ntcon 分别是相应的比较器的计数器值，而不同扇区时间分配如表 2-5 所示，并将这三个值写入相应的比较寄存器就完成了整个 SVPWM 的算法。

表 2-5  不同扇区比较器的计数值

扇区	1	2	3	4	5	6
Ta	Ntaon	Ntbon	Ntcon	Ntcon	Ntbon	Ntaon
Tb	Ntbon	Ntaon	Ntaon	Ntbon	Ntcon	Ntcon
Tc	Ntcon	Ntcon	Ntbon	Ntaon	Ntaon	Ntbon

1. 1. SVPWM 物理含义

SVPWM 实质是一种对在三相正弦波中注入了零序分量的调制波进行规则采样的一种变形SPWM。但SVPWM 的调制过程是在空间中实现的，而SPWM是在 ABC 坐标系下分相实现的；SPWM 的相电压调制波是正弦波，而SVPWM没有明确的相电压调制波，是隐含的。为了揭示 SVPWM 与 SPWM 的内在联系，需求出 SVPWM 在 ABC 坐标系上的等效调制波方程，也就是将 SVPWM 的隐含调制波显化。

为此，本文对其调制波函数进行了详细的推导。 由表 3-2 我们知道了各扇区的矢量发送顺序：

奇数区依次为：U 0 ，U k ，U k+1 ，U 7 ，U k+1 ，U k ，U 0 

偶数区依次为：U 0 ，U k+1 ，U k ，U 7 ，U k ，U k+1 ，U 0 

利用空间电压矢量近似原理，可总结出下式：

式中 m 仍为 SVPWM 调制系数，利用以上各式就可得到在第Ⅰ扇区的各相电压平均值：

同样可以推导出其它扇区的调制波函数，其相电压调制函数如下：

（2-44）

其线电压的调制波函数为：

（2-45）

从相电压调制波函数（2-44）来看，输出的是不规则的分段函数，为马鞍波形。从线电压调制波函数（2-45）来看其输出的则是正弦波形。