98. 验证二叉搜索树(两种方法)
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
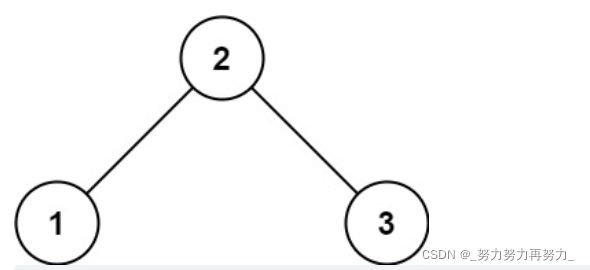
输入:root = [2,1,3]
输出:true
示例 2:
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/validate-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
一开始写的错误代码,我是想着,当某个节点的左子树大于等于父亲节点或者右子树小于等于右子节点的时候,返回 false,其他情况就是二叉搜索树,但是有一种情况没有考虑进去,就是这样的情况:

如图,满足左孩子小,右孩子大,但是 3 是小于 5 的,不应该出现在右子树中,所以此方法不可用,寻找新的方法。
public boolean Dfs(TreeNode root) {
if (root == null) {
return true;
}
if (root.left != null && root.left.val >= root.val) {
return false;
} else if (root.right != null && root.right.val <= root.val) {
return false;
}
return Dfs(root.left) && Dfs(root.right);
}
于是可以想到,当记录下当前左子树的最大值,右子树的最小值的时候,只要让左子树的点都小于该最大值,右子树的点都大于该最小值,即可完成判断。
于是有以下代码(需要用 long 类型,int 可能会超范围,比如传入的某个点为 2147438647 的时候,就很容易超范围)刚开始传递一个最小值,一个最大值,如果此时节点,比最小值小或者比最大值大,说明不满足题意返回 false,然后递归判断左右子树即可,在判断左子树的时候,传入当前节点的值为最大值
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
return Dfs(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean Dfs(TreeNode root, long lower, long upper) {
if (root == null) {
return true;
}
if (root.val <= lower || root.val >= upper) {
return false;
}
return Dfs(root.left, lower, root.val) && Dfs(root.right, root.val, upper);
}
}
递归解法完成,以下是中序遍历的解法,递归就不说了,太简单不会考的,说一下迭代的方法:
由于 Long 不能转换成 Integer,所以这里用 double 来替换,道理都一样,中序遍历:左根右,在根节点的时候,与前面的节点的值判断,是否大于,如果不大于,说明不是二叉搜索树。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
double d = -Double.MAX_VALUE;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (root.val <= d) {
return false;
}
d = root.val;
root = root.right;
}
return true;
}
}