【C++二叉树】进阶OJ题

【C++二叉树】进阶OJ题

作者：爱写代码的刚子

时间：2023.9.6

前言：本篇博客总结了一些二叉树有关的一些中等难度OJ题，总结这些题的解题思路

---

1.二叉树的层序遍历II

题目链接

示例代码

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> vv;
        if(!root)
        {
            return vv;
        }
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty())
        {
            int curlevel = q.size();
            vv.push_back(vector<int> ());
            while(curlevel--)
            {
                TreeNode *front=q.front();
                vv.back().push_back(front->val);
                q.pop();

                if(front->left)
                {
                    q.push(front->left);
                }
                if(front->right)
                {
                    q.push(front->right);
                }
            }
        }
        reverse(vv.begin(),vv.end());
        return vv;
    }
};

解题思路

1. 选择使用队列来实现

2. 

3. 注意这里使用变量curlevel来记录每层的元素个数，并且第二个while循环中需要curlevel来计数，因为题目中要求返回 vector，所以记录每层的元素个数是必要的。

4. 由于题目要求返回自底向上的层序遍历，所以我们还需要reverse函数将vector容器进行反转。

2.二叉搜索树与双向链表

题目链接

示例代码

class Solution {
public:
	void test(TreeNode* cur,TreeNode*& prev)
	{
		if(cur==nullptr)
		{
			return;
		}
		test(cur->left,prev);
		cur->left=prev;
		if(prev)//注意prev可能为nullptr
		{
			prev->right=cur;
		}
		prev=cur;
		test(cur->right,prev);
	}


    TreeNode* Convert(TreeNode* pRootOfTree) {
		TreeNode*prev=nullptr;
		test(pRootOfTree,prev);
		TreeNode* leftover=pRootOfTree;
		while(leftover&&leftover->left)
		{
			leftover=leftover->left;
		}
		return leftover;
    }
};

解题思路

1. 采用中序遍历
2. 由于二叉树遍历的特殊性，我们无法找到下一个遍历的对象，所以我们设立新旧指针：cur和prev，由于根节点prev未知，所以我们传入nullptr
3. 我们让cur指针先走，对旧节点的指针朝向进行修改（prev的left和right指针）
4. 如图：

本质其实就是让cur先走，记录先前节点（prev），并修改先前节点的指针朝向。

3.从前序与中序遍历序列构造二叉树

题目链接

示例代码

class Solution {
public:
    TreeNode* test(vector<int>& preorder, vector<int>& inorder,int begini,int& prei,int endi)
    {
        if(begini>endi)
        {
            return nullptr;
        }
        TreeNode* root=new TreeNode(preorder[prei]);
        int rooti=begini;
        while(rooti<=endi)
        {
            if(preorder[prei]==inorder[rooti])
            {
                break;
            }
            else
            {
                ++rooti;
            }
        }
        ++prei;
        root->left=test(preorder, inorder,begini,prei,rooti-1);
        root->right=test(preorder, inorder,rooti+1,prei,endi);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int i=0;
        return test(preorder,inorder,0,i,preorder.size()-1);
    }
};

解题思路

1. 前序遍历可以确定根节点的位置

2. 确定了根再去中序遍历里找到对应的根

3. 两者遍历的图示：

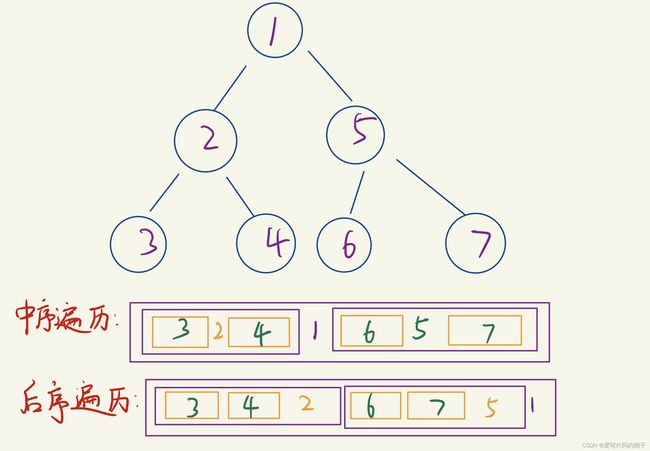
4. 观察图示结构，我们可以将前序遍历中的数据从左到右进行遍历，一次将遍历的节点作为根节点

5. 观察图示结构，我们利用前序遍历中定的根节点在中序遍历中找到对应的位置，用中序遍历的结构来进行递归（类似分治）

6. 递归的结束条件就是递归到子叶节点时，子叶节点再进行递归，递归区间有误。（begini>endi）

4.从中序与后序遍历序列构造二叉树

题目链接

示例代码

class Solution {
public:
    TreeNode*test(vector<int>& inorder, vector<int>& postorder,int begini,int& prei,int endi){

        if(begini>endi)
        {
            return nullptr;
        }
        TreeNode*root=new TreeNode(postorder[prei]);
        int rooti=endi;
        while(rooti>=begini)
        {
            if(inorder[rooti]==postorder[prei])
            {
                break;
            }
            --rooti;
        }
        --prei;
        root->right=test(inorder, postorder,rooti+1,prei,endi);
        root->left=test(inorder, postorder,begini,prei,rooti-1);
        //root->right=test(inorder, postorder,rooti+1,prei,endi);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int i=postorder.size()-1;
        return test(inorder, postorder,0,i,i);
    }
};

解题思路

1. 思路与《从中序与后序遍历序列构造二叉树》类似，先画图：

2. 我们发现与《从中序与后序遍历序列构造二叉树》这道题中的结构类似，所以考虑后序遍历序列从右往左遍历，依次将访问的节点作为根节点

3. 注意！后序遍历中访问完根节点后访问的是右节点，所以我们应先构造右子树，将《从中序与后序遍历序列构造二叉树》题中的示例代码中两个递归入口交换顺序即可

5.二叉树的前序遍历（非递归迭代实现）

题目链接

示例代码

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* tmp=root;
        while(tmp||!st.empty())
        {
            while(tmp)
            {
                v.push_back(tmp->val);
                st.push(tmp);
                tmp=tmp->left;
            }

            tmp=st.top()->right;
            st.pop();
        }
        return v;
    }
};

解题思路

1. 使用vector和stack
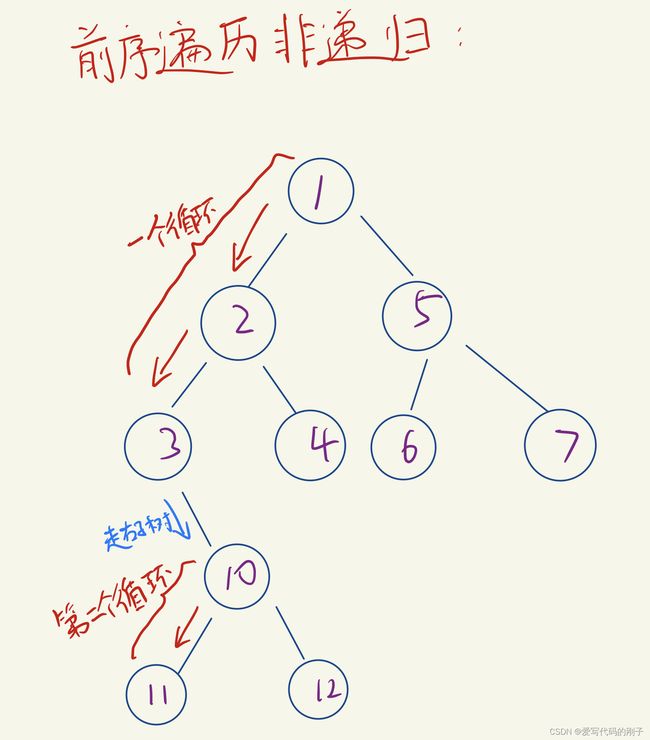
2. 先将二叉树最左边的节点push进栈，将节点储存的值push_back进vector
3. 再取出栈顶元素，控制指针进入栈顶元素节点的右子树，并pop该栈顶元素，重复以上步骤
4. 图示：

6.二叉树的中序遍历（非递归迭代实现）

题目链接

示例代码

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur=root;
        while(cur||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            TreeNode* top=st.top();
            v.push_back(top->val);
            cur=top->right;
            st.pop();
        }
        return v;
    }
};

解题思路

过程与前序遍历类似，只是访问的时机不同，中序遍历要在所有左子树push进栈后再进行访问，并pop栈顶元素

7二叉树的后序遍历（非递归迭代实现）

题目链接

示例代码

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
         stack<TreeNode*> st;
        vector<int> v;
        TreeNode* cur=root;
        TreeNode* prev=nullptr;
        while(cur||!st.empty())
        {
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            TreeNode* top=st.top();
            if(top->right==nullptr||top->right==prev)
            {
                prev=top;
                v.push_back(top->val);
                st.pop();
            }
            else
            {
                cur=top->right;
            }
        }
        return v;
    }
};

解题思路

1. 我们需要设定访问时机，当右子树已经访问完了或者没有右子树时进行访问。
2. 如何判读右子树是否访问完了：要引入prev指针记录上一个访问的节点，判断prev是否等于当前节点（top）的右子树。
3. 注意这里使用的是if…else语句，并不是无脑cur=top->right

---