【代码随想录】【LeetCode】自学笔记 10 - 贪心算法

贪心算法介绍

贪心算法一般分为如下四步：

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解
其实这个分的有点细了，真正做题的时候很难分出这么详细的解题步骤，可能就是因为贪心的题目往往还和其他方面的知识混在一起。
贪心没有套路，说白了就是常识性推导加上举反例。

455.分发饼干

// /*这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。
// 思考的过程，想清楚局部最优，想清楚全局最优，感觉局部最优是可以推出全局最优，并想不出反例，那么就试一试贪心。
// 注意，i 和 j 不是同步增减的！所以不能写在一个for的括号里
// // 时间复杂度：O(nlogn)
// // 空间复杂度：O(1)
// class Solution {
// public:
//     int findContentChildren(vector& g, vector& s) {
//         sort(g.begin(), g.end());//胃口
//         sort(s.begin(), s.end());//饼干
//         int index = s.size() - 1; // 饼干数组的下标
//         int result = 0;
//         for (int i = g.size() - 1; i >= 0; i--) {
//             if (index >= 0 && s[index] >= g[i]) {
//                 result++;
//                 index--;
//             }
//         }
//         return result;
//     }
// };
class Solution{
    public:
    int findContentChildren(vector<int>& g, vector<int>& s){
        int result = 0;
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int j = s.size()-1;


        for (int i = g.size() - 1; i >= 0; i--){

            if ( j >= 0 && g[i] <= s[j]) {
                result++;
                j--;
            }
        }
        return result;
    }
};

376.摆动数列

// // 局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。
// // 整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。
// // 局部最优推出全局最优，并举不出反例，那么试试贪心！

// // （为方便表述，以下说的峰值都是指局部峰值）
// // 实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）
// // 这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点。

// // 本题代码实现中，还有一些技巧，例如统计峰值的时候，数组最左面和最右面是最不好统计的。
// // 例如序列[2,5]，它的峰值数量是2，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
// // 所以可以针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即 preDiff = 0
// //思路2（动态规划）（以下几道题都是，但没看）
// class Solution {
// public:
//     int wiggleMaxLength(vector& nums) {
//         if (nums.size() <= 1) return nums.size();
//         int curDiff = 0; // 当前一对差值
//         int preDiff = 0; // 前一对差值
//         int result = 1; 
//         for (int i = 0; i < nums.size() - 1; i++) {
//             curDiff = nums[i + 1] - nums[i];
//             // 出现峰值
//             if ((curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0)) {
//                 result++;
//                 preDiff = curDiff;
//             }
//         }
//         return result;
//     }
// };
class Solution{
    public:
    int wiggleMaxLength(vector<int>& nums){
        if (nums.size() <= 1) return nums.size();///特殊情况
        int result = 1; // 记录峰值个数，序列默认序列最右边有一个峰值
        int curDiff = 0;
        int preDiff = 0;
        for(int i = 0; i< nums.size() - 1; i ++){涉及到i±1的操作，要注意for里面i的终点了
            curDiff = nums[i+1]-nums[i];
            if( (curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0) ) 
            {
                result++;//注意=0的情况也算数的！
                preDiff = curDiff;//注意变化了才更新prediff！
            }
        }
        return result;
    }
};

122.买卖股票的最佳时机 II

// // 其实我们需要收集每天的正利润就可以
// //本题中理解利润拆分是关键点！ 不要整块的去看，而是把整体利润拆为每天的利润。

//         for (int i = 1; i < prices.size(); i++) {
//             result += max(prices[i] - prices[i - 1], 0);

class Solution{
    public:
    int maxProfit( vector<int>& prices){
        int result = 0;
        for(int i = 0; i < prices.size() - 1; i++){
            result += max(0,prices[i+1]-prices[i] );
        }
        return result;
    }

};

55. 跳跃游戏

/*那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。

贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。
*/
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int cover = 0;
        if (nums.size() == 1) return true; // 只有一个元素，就是能达到
        for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover
        【第一次出现】不断更新 for 的终点，类似回溯or动态规划？
            cover = max(i + nums[i], cover);
            if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了//-1，注意此时是下标，所以-1
        }
        return false;
    }
};

45.跳跃游戏II

// // 以最小的步数增加最大的覆盖范围，直到覆盖范围覆盖了终点，这个范围内最小步数一定可以跳到，不用管具体是怎么跳的，不纠结于一步究竟跳一个单位还是两个单位。
// //一步一步（i）遍历整个数组[0~倒数第二位]，在每一步记录能到的最大的终点，这个终点最大只能是数组终点，如果不够大，后续步数会追上，此时ans ++
注意和前一题（跳跃游戏1）的 for 等等参数都不同，需要再次对比着看
// class Solution {
// public:
//     int jump(vector& nums) {
//         int ans = 0;            // 记录走的最大步数
//         int curDistance = 0;    // 当前覆盖的最远距离下标
//         int nextDistance = 0;   // 下一步覆盖的最远距离下标
//         for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1，这是关键所在
//             nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
//             if (i == curDistance) {                 // 遇到当前覆盖的最远距离下标
//                 curDistance = nextDistance;         // 更新当前覆盖的最远距离下标
//                 ans++;
//             }
//         }
//         return ans;
//     }
// };

1005. K 次取反后最大化的数组和

// // 第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
// // 第二步：从前向后遍历，遇到负数将其变为正数，同时 K--
// // 第三步：如果 K 还大于0，那么反复转变数值最小的元素，将 K 用完（若 k 大于0，只需考虑是奇数的情况）
// // 第四步：求和
// //局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。局部最优可以推出全局最优

// class Solution {
// static bool cmp(int a, int b) {//【第一次出现！ （默认private？）static cmp 】
//     return abs(a) > abs(b);//将 sort 的规则改成绝对值的降序排列（从大到小）//return a
// }
// public:
//     int largestSumAfterKNegations(vector& A, int K) {
//         sort(A.begin(), A.end(), cmp);       // 第一步
//         for (int i = 0; i < A.size(); i++) { // 第二步
//             if (A[i] < 0 && K > 0) {
//                 A[i] *= -1;
//                 K--;
//             }
//         }
//         if (K % 2 == 1) A[A.size() - 1] *= -1; // 第三步
//         int result = 0;
//         for (int a : A) result += a;        // 第四步
//         return result;
//     }
// };
class Solution{
    static bool cmp (int a, int b) {
        return abs(a)>abs(b);///函数不像 if 必须有大括号
    }
    public:
    int largestSumAfterKNegations(vector<int>& nums, int K){
        sort(nums.begin(), nums.end(), cmp);
        for(int i = 0; i < nums.size(); i ++){
            if (nums[i] < 0 && K > 0) {//还是加上{}保险。。。
                nums[i] *= -1;///&& K > 0
                K--;
            }
        }

        if (K%2 == 1) nums[nums.size()-1] *= -1;
        int sum = 0;
        for(int i = 0; i < nums.size(); i++){
            sum += nums[i];
        }
          //for (int a : nums) sum += a;        //更简单！       
        return sum;
    }   
};

134. 加油站

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int totalSum = 0;
        int start = 0;
        for (int i = 0; i < gas.size(); i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {   // 当前累加res t[i]和 curSum一旦小于0
                start = i + 1;  // 起始位置更新为i+1
                curSum = 0;     // curSum 从0开始
            }
        }
        if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
        return start;
    }
};
//首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest [i]相加一定是大于等于零的。
//如果gas 的总和小于cost 总和，那么无论从哪里出发，一定是跑不了一圈的
//why ??需要重理解。目前理解只能是举不出反例。
//有一个环形路上有n个站点； 每个站点都有一个好人或一个坏人； 好人会给你钱，坏人会收你一定的过路费，如果你带的钱不够付过路费，坏人会跳起来把你砍死； 问：从哪个站点出发，能绕一圈活着回到出发点?(vectorint 不能直接相减)

135. 分发糖果

// 这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼。
// 此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果，全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果
// ///相同评分的相邻孩子，可以获得不同数量的糖果（从而可以2,1,1,1,2，减少花费的糖果总数
// 再确定左孩子大于右孩子的情况（从后向前遍历）
// 遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？
// 因为如果从前向后遍历，根据 ratings [i + 1] 来确定 ratings [i] 对应的糖果，那么每次都不能利用上前一次的比较结果了。局部最优：取candyVec [i + 1] + 1 和 candyVec [i] 最大的糖果数量，保证第i个小孩的糖果数量即大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。
// 局部最优可以推出全局最优。
// 所以就取 candyVec [i + 1] + 1 和 candyVec [i] 最大的糖果数量，candyVec [i]只有取最大的才能既保持对左边candyVec [i - 1]的糖果多，也比右边 candyVec [i + 1]的糖果多。

// 这在leetcode上是一道困难的题目，其难点就在于贪心的策略，如果在考虑局部的时候想两边兼顾，就会顾此失彼。
// 那么本题我采用了两次贪心的策略：
// 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
// 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。
// 这样从局部最优推出了全局最优，即：相邻的孩子中，评分高的孩子获得更多的糖果。
class Solution {
public:
    int candy(vector<int>& ratings) {
        vector<int> candyVec(ratings.size(), 1);//【第一次见】初始化vector的初始值和大小为1
        // 从前向后
        for (int i = 1; i < ratings.size(); i++) {//右大改右，跳过第一个
            if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
        }
        // 从后向前
        for (int i = ratings.size() - 2; i >= 0; i--) {//左大改左，跳过最后一个
            if (ratings[i] > ratings[i + 1] ) {candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);}    
        }
        // 统计结果
        int result = 0;
        for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];
        return result;
    }
};

860.柠檬水找零

// 情况一：账单是5，直接收下。
// 情况二：账单是10，消耗一个5，增加一个10
// 情况三：账单是20，优先消耗一个10和一个5，如果不够，再消耗三个5
// 此时大家就发现 情况一，情况二，都是固定策略，都不用我们来做分析了，而唯一不确定的其实在情况三。
// 所以局部最优：遇到账单20，优先消耗美元10，完成本次找零。全局最优：完成全部账单的找零。

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        int five = 0, ten = 0, twenty = 0;
        for (int bill : bills) {
            // 情况一
            if (bill == 5) five++;
            // 情况二
            if (bill == 10) {
                if (five <= 0) return false;
                ten++;
                five--;
            }
            // 情况三
            if (bill == 20) {
                // 优先消耗10美元，因为5美元的找零用处更大，能多留着就多留着
                if (five > 0 && ten > 0) {
                    five--;
                    ten--;
                    twenty++; // 其实这行代码可以删了，因为记录20已经没有意义了，不会用20来找零
                } else if (five >= 3) {
                    five -= 3;
                    twenty++; // 同理，这行代码也可以删了
                } else return false;
            }
        }
        return true;
    }
};

406.根据身高重建队列

// /* //insert (pos,elem)	在迭代器 pos 指定的位置之前插入一个新元素elem，并返回表示新插入元素位置的迭代器
// // //关于出现两个维度一起考虑的情况，我们已经做过两道题目了，另一道就是135. 分发糖。
// // 其技巧都是确定一边然后贪心另一边，两边一起考虑，就会顾此失彼。
// // 最后我给出了两个版本的代码，可以明显看是使用C++中的list（底层链表实现）比vector（数组）效率高得多。
// 排序完的people： [[7,0], [7,1], [6,1], [5,0], [5,2]，[4,4]]
// 插入的过程：
// 插入[7,0]：[[7,0]]
// 插入[7,1]：[[7,0],[7,1]]
// 插入[6,1]：[[7,0],[6,1],[7,1]]
// 插入[5,0]：[[5,0],[7,0],[6,1],[7,1]]
// 插入[5,2]：[[5,0],[7,0],[5,2],[6,1],[7,1]]
// 插入[4,4]：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

// */
// class Solution {
// public:
//     // 身高从大到小排（身高相同k小的站前面）
//     static bool cmp(const vector& a, const vector& b) {
//         if (a[0] == b[0]) return a[1] < b[1];
//         return a[0] > b[0];
//     }
//     vector> reconstructQueue(vector>& people) {
//         sort (people.begin(), people.end(), cmp);
//         list> que; // list 插入效率比vector 高的多
//         for (int i = 0; i < people.size(); i++) {

//             int position = people[i][1]; // 插入到下标为position 的位置
//             std::list>::iterator it = que.begin();
//             while (position--) it++; // 寻找在插入位置
//             que.insert(it, people[i]);/insert()：在指定位置插入新元素；

//         }

//         return vector>(que.begin(), que.end());//list>最后转成v>
//     }
// };
精简版
class Solution{
    public:
    static bool cmp(const vector<int>& a, const vector<int>& b){
        if (a[0] == b[0]) return a[1]<b[1];
        return a[0]>b[0];
    }
    vector<vector<int>>  reconstructQueue(vector<vector<int>>& people){
        sort(people.begin(), people.end(), cmp);
        list<vector<int>> que;

        for(int i = 0; i < people.size(); i++){
            int position = people[i][1];
            std::list<vector<int>>::iterator it = que.begin();
            while (position--) it++;
            que.insert(it, people[i]);
        }


        return vector<vector<int>> (que.begin(), que.end());
        }
};

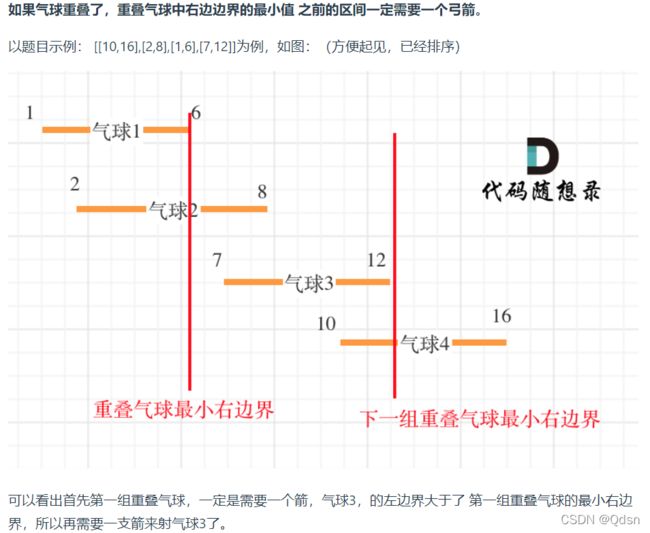
452 用最少数量的箭引爆气球

/*
只射重叠最多的气球，用的弓箭一定最少
试一试贪心吧！局部最优：当气球出现重叠，一起射，所用弓箭最少。全局最优：把所有气球射爆所用弓箭最少。

为了让气球尽可能的重叠，需要对数组进行【排序】。
那么按照气球起始位置排序，还是按照气球终止位置排序呢？
其实都可以！只不过对应的遍历顺序不同，我就按照气球的起始位置排序了，从前向后遍历气球数组，靠左尽可能让气球重复。
寻找重复的气球，寻找重叠气球最小右边界。
*/
class Solution {
private:
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0];
    }
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if (points.size() == 0) return 0;
        sort(points.begin(), points.end(), cmp);

        int result = 1; // points 不为空至少需要一支箭
        for (int i = 1; i < points.size(); i++) {
            if (points[i][0] > points[i - 1][1]) {  // 气球i和气球i-1不挨着，注意这里不是>=
                result++; // 需要一支箭
            }
            else {  // 气球i和气球i-1挨着
                points[i][1] = min(points[i - 1][1], points[i][1]); 
/// 更新重叠气球最小右边界///从最新（左）一个不重叠气球开始，"统一"后面有重叠的气球的右边界
            }
        }
        return result;
    }
};

435. 无重叠区间

/*[此时问题就是要求非交叉区间的(最大个数)。]
题目只是要求移除区间的个数，没有必要去真实的模拟删除区间！
我来按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
相信很多同学看到这道题目都冥冥之中感觉要排序，但是究竟是按照右边界排序，还是按照左边界排序呢？
这其实是一个难点！
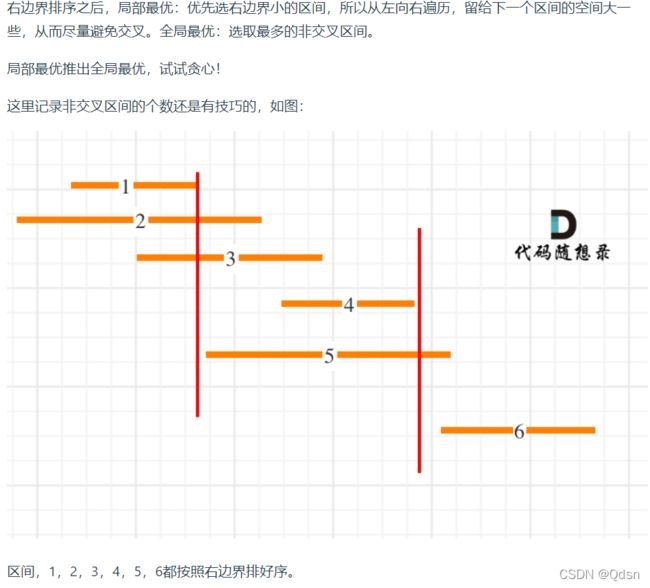
按照右边界排序，就要从左向右遍历，因为右边界越小越好，只要右边界越小，留给下一个区间的空间就越大，所以从左向右遍历，优先选右边界小的
按照左边界排序，就要从右向左遍历，因为左边界数值越大越好（越靠右），这样就给前一个区间的空间就越大，所以可以从右向左遍历。
我来按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。

贪心就是这样，代码有时候很简单（不是指代码短，而是逻辑简单），但想法是真的难！
总结如下难点：
难点一：一看题就有感觉需要排序，但究竟怎么排序，按左边界排还是右边界排。
难点二：排完序之后如何遍历，如果没有分析好遍历顺序，那么排序就没有意义了。
难点三：直接求重复的区间是复杂的，转而求最大非重复区间个数。
难点四：求最大非重复区间个数时，需要一个分割点来做标记

本题其实和452.用最少数量的箭引爆气球非常像，[(最少数量的)弓箭的数量就相当于是非交叉区间的数量]，只要把弓箭那道题目代码里射爆气球的判断条件加个等号（认为[0，1][1，2]不是相邻区间），然后用总区间数减去弓箭数量 就是要移除的区间数量了。?????思路完全相反才对吧？所以其实是一样的，二者return 总和是区间总数。所以靠左sort 和靠右sort 一样能用。。。
*/
class Solution {
public:
    // 按照区间右边界排序气球是按左边界
    static bool cmp (const vector<int>& a, const vector<int>& b) {
        return a[1] < b[1];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) return 0;
        sort(intervals.begin(), intervals.end(), cmp);
        int count = 1; // 记录非交叉区间的个数
        int end = intervals[0][1]; // 记录区间分割点
        for (int i = 1; i < intervals.size(); i++) {
            if (end <= intervals[i][0]) {
                end = intervals[i][1];
                count++;
            }
        }
        return intervals.size() - count;
    }
};

763 划分字母区间

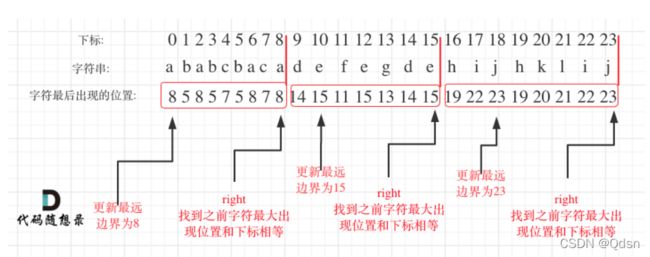
可以分为如下两步：

统计每一个字符最后出现的位置
从头遍历字符，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了，则找到了分割点
算法很巧妙！！！！

class Solution {
public:
    vector<int> partitionLabels(string S) {
        int has[26] = {0}; // 
        for (int i = 0; i < S.size(); i++) { // 统计每一个字符最后出现的位置
            has[S[i] - 'a'] = i;///!!!!  i为字符，has[i]为字符出现的最后位置
        }
        vector<int> result;
        int left = 0;
        int right = 0;
        for (int i = 0; i < S.size(); i++) {
            right = max(right, has[S[i] - 'a']); // 找到字符出现的最远边界
            if (i == right) {
                result.push_back(right - left + 1);
                left = i + 1;
            }
        }
        return result;
    }
};

738. 单调递增的数字

/*
例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]--，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。
*/
class Solution {
public:
    int monotoneIncreasingDigits(int N) {
        string strNum = to_string(N);// 【第一次见】int 转string ！！！！ to_string(N)
        int flag = strNum.size();// flag用来标记赋值9从哪里开始//设置为这个默认值，为了防止第二个for循环在flag没有值的情况下执行
        for (int i = strNum.size() - 1; i > 0; i--) {
            if (strNum[i - 1] > strNum[i] ) {
                flag = i;
                strNum[i - 1]--;
            }
        }
        for (int i = flag; i < strNum.size(); i++) {
            strNum[i] = '9';
        }
        return stoi(strNum);// 【第一次见】string 转int ！！！！ stoi(S)
    }
};

968 监控二叉树（困难）

/**
摄像头可以覆盖上中下三层，如果把摄像头放在叶子节点上，就浪费的一层的覆盖。所以把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。;为什么不从头结点开始看起呢，为啥要从叶子节点看呢?因为头结点放不放摄像头也就省下一个摄像头， 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。大体思路就是从低到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。
两个难点：
二叉树的遍历
如何隔两个节点放一个摄像头
 */
// 版本一
class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {

        // 空节点，该节点有覆盖
        if (cur == NULL) return 2;

        int left = traversal(cur->left);    // 左
        int right = traversal(cur->right);  // 右

        // 情况1
        // 左右节点都有覆盖
        if (left == 2 && right == 2) return 0;

        // 情况2
        // left == 0 && right == 0 左右节点无覆盖
        // left == 1 && right == 0 左节点有摄像头，右节点无覆盖
        // left == 0 && right == 1 左节点有无覆盖，右节点摄像头
        // left == 0 && right == 2 左节点无覆盖，右节点覆盖
        // left == 2 && right == 0 左节点覆盖，右节点无覆盖
        if (left == 0 || right == 0) {
            result++;
            return 1;
        }

        // 情况3
        // left == 1 && right == 2 左节点有摄像头，右节点有覆盖
        // left == 2 && right == 1 左节点有覆盖，右节点有摄像头
        // left == 1 && right == 1 左右节点都有摄像头
        // 其他情况前段代码均已覆盖
        if (left == 1 || right == 1) return 2;

        // 以上代码我没有使用else，主要是为了把各个分支条件展现出来，这样代码有助于读者理解
        // 这个 return -1 逻辑不会走到这里。
        return -1;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        // 情况4
        if (traversal(root) == 0) { // root 无覆盖
            result++;
        }
        return result;
    }
};